Презентация "Объём. Цилиндр, призма" по математике – проект, доклад
Презентацию на тему "Объём. Цилиндр, призма" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 24 слайд(ов).
Слайды презентации
Список похожих презентаций
Объём цилиндра и конуса
«Не стыдись спросить – не знать еще стыднее!» Японская пословица. В игре участвуют 2 команды. Капитан команды выбирает номер задания, и команда приступает ...Объём цилиндра и конуса задачи практического содержания
№ 1 1 вариант. Выполните рисунок цилиндра, обозначьте на рисунке радиус, высоту. 2 вариант. Выполните рисунок конуса, обозначьте на рисунке образующую, ...Объём цилиндра
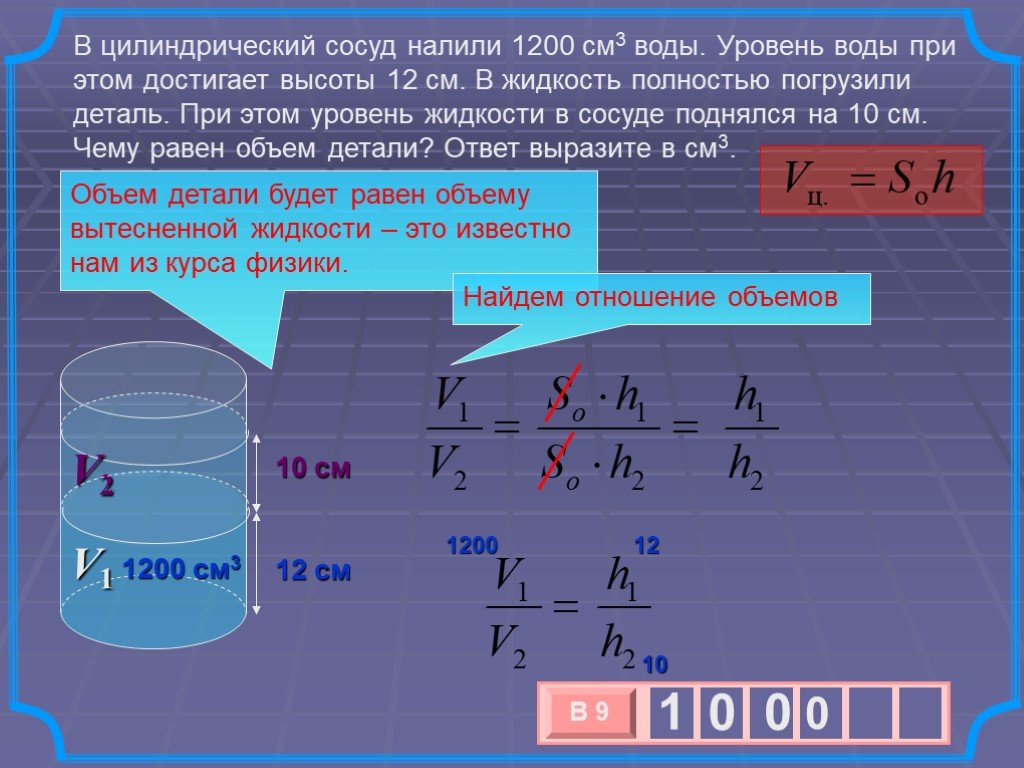
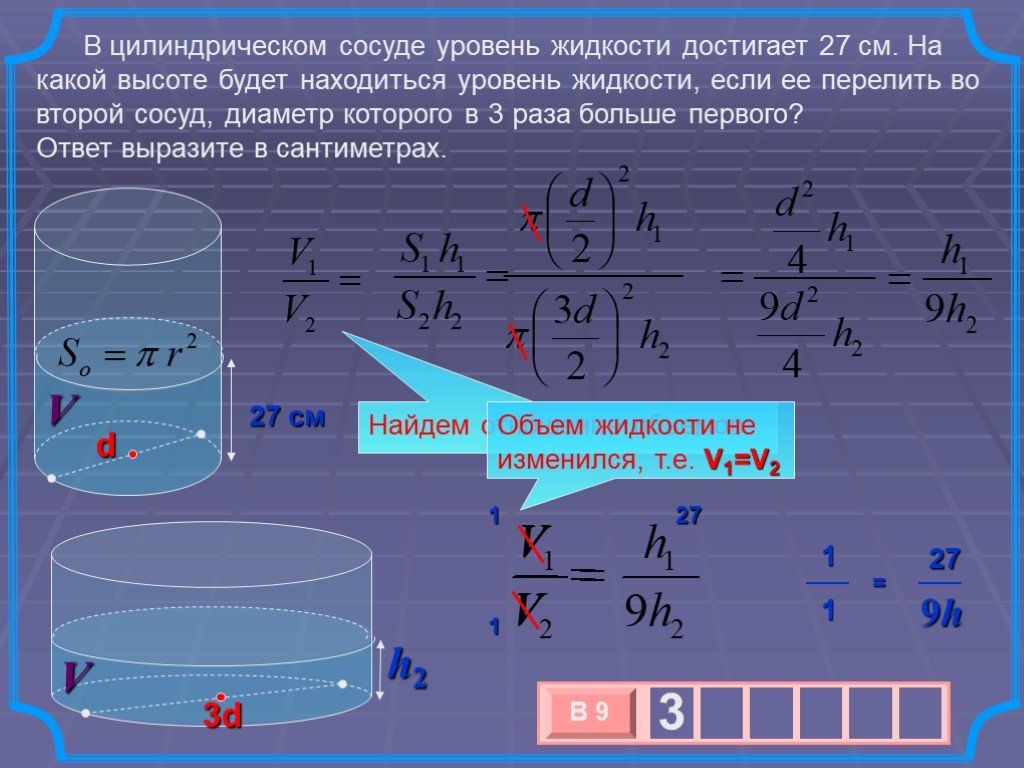
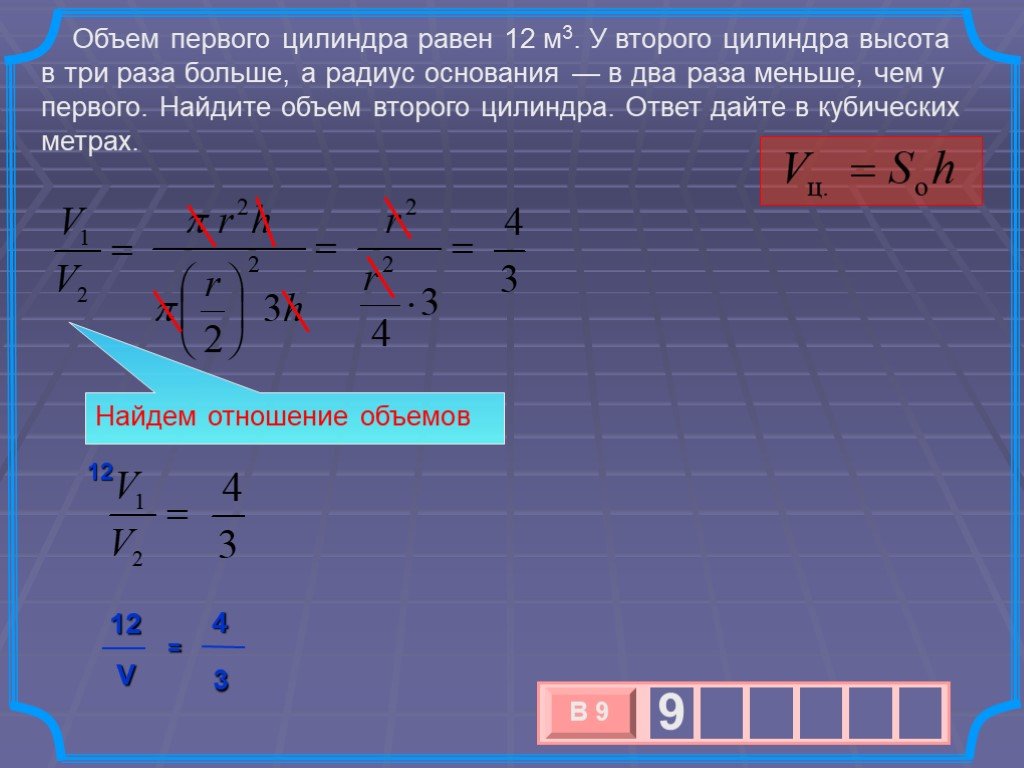
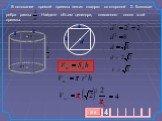
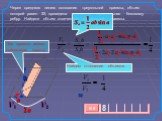
Объём цилиндра равен произведению площади основания на высоту. V=SH=пR^2H. . Решить задачу. Дано: АВ = 26см АС = 12 см Найти: V Решение: V=SH=пR^2H. ...Объём цилиндра
Цилиндр: история. Слово "цилиндр" происходит от греческого kylindros, что означает "валик", "каток " …. Цилиндры из жизни. Цилиндры-башни. Водовзводная ...Конус, пирамида, призма, цилиндр.
Цели урока. Учить учащихся навыкам и умениям определять название геометрических тел, мысленно расчленять предметы на составляющие его геометрические ...Решение задач по теме Цилиндр
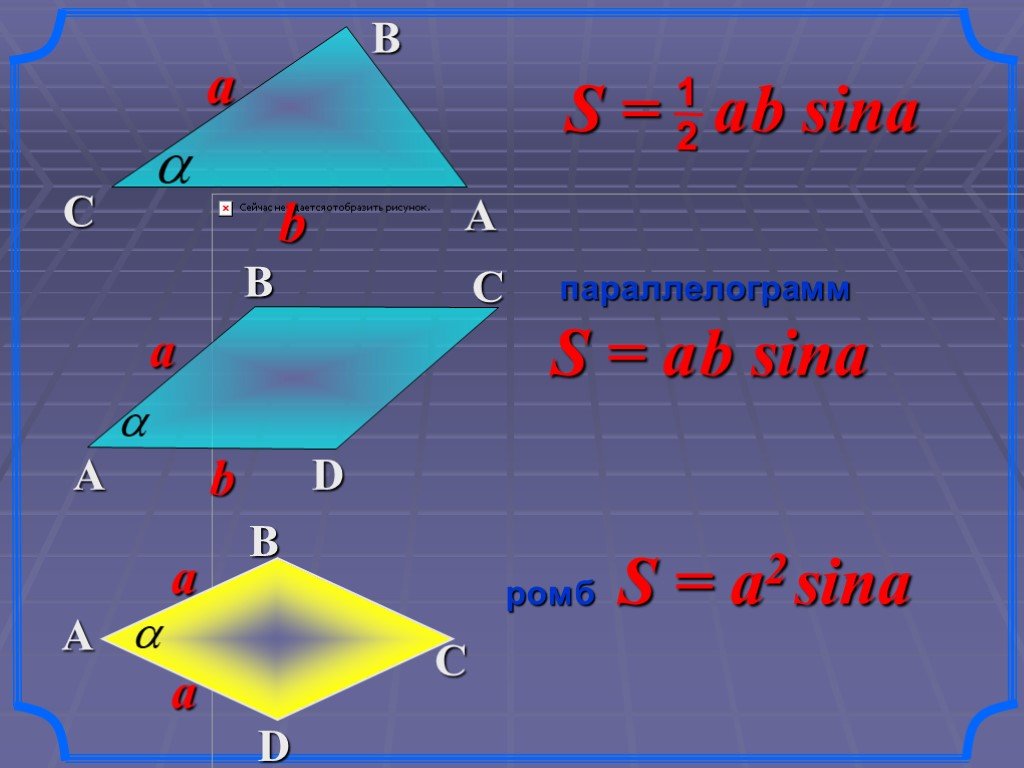
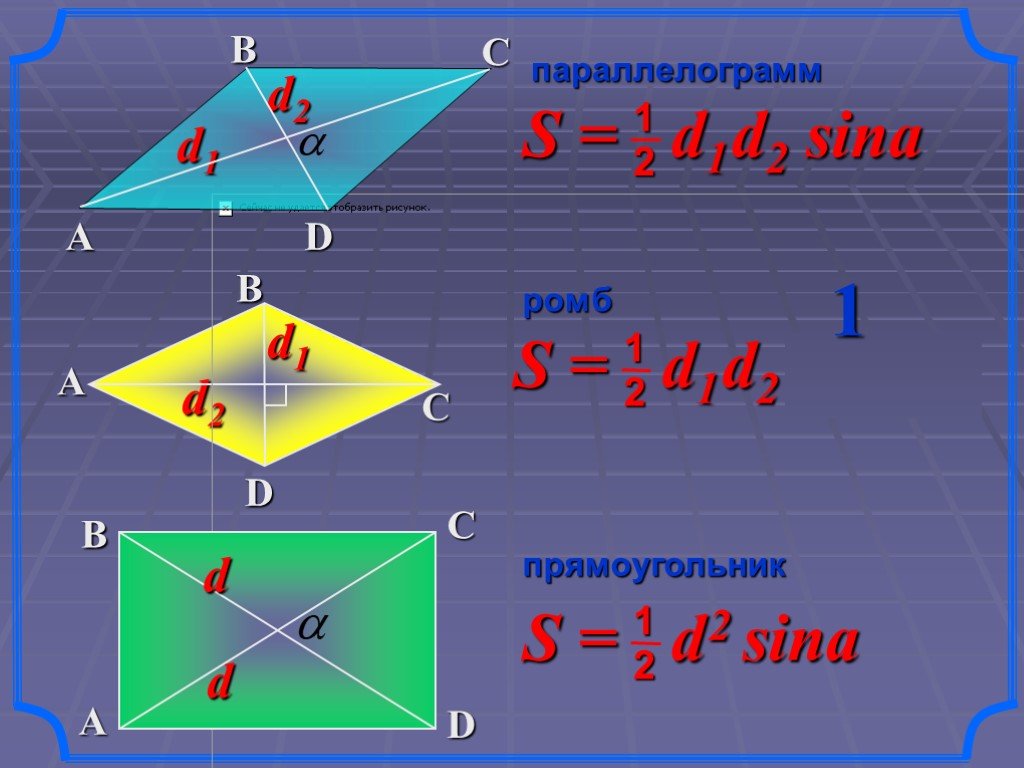
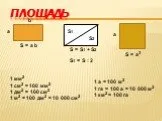
L m. Общая цилиндрическая поверхность, её направляющая L и образующая m. Общее определение цилиндрического тела. 1. Наклонный круговой цилиндр. ...Площадь. Объём
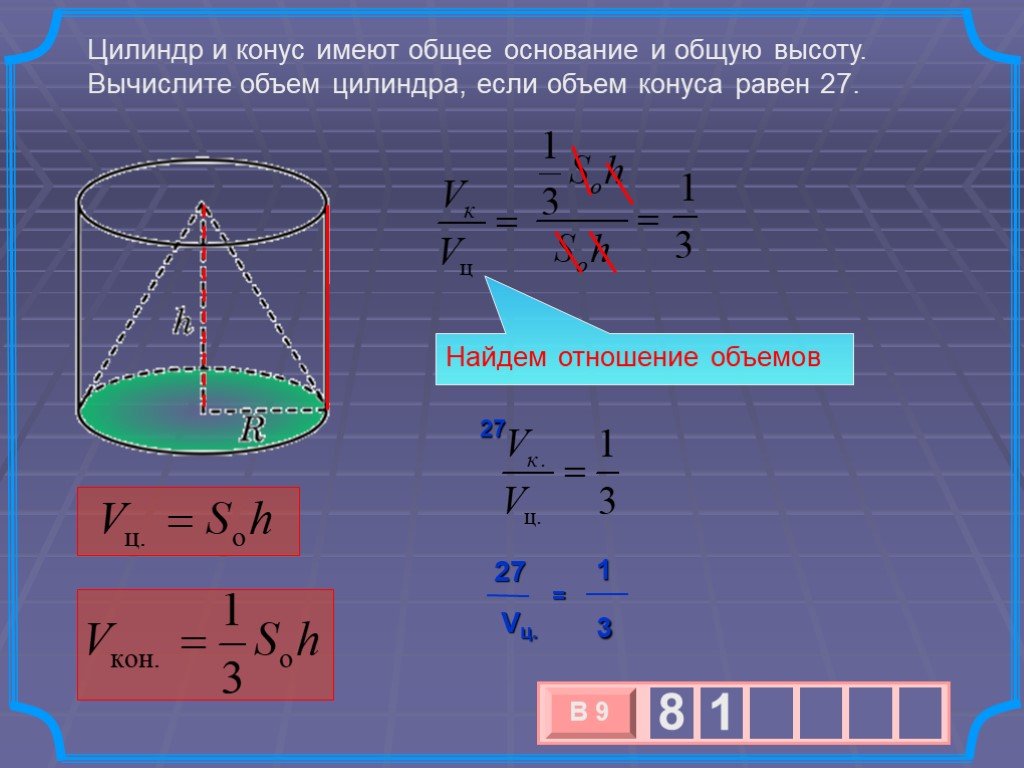
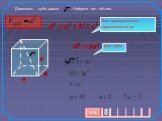
Объем. Вершины, ребра, грани. Прямоугольный параллелепипед V = a b c. Куб V = a3 c. 1 мм3 1 см3 = 1 000 мм3 1 дм3 = 1 л = 1 000 см3 1 м3 = 1 000 дм3 ...Объём конуса
1. Высота конуса равна 8 см. На каком расстоянии от вершины конуса надо провести плоскость, параллельную основанию, чтобы площадь сечения была равна ...Цилиндр, шар, конус
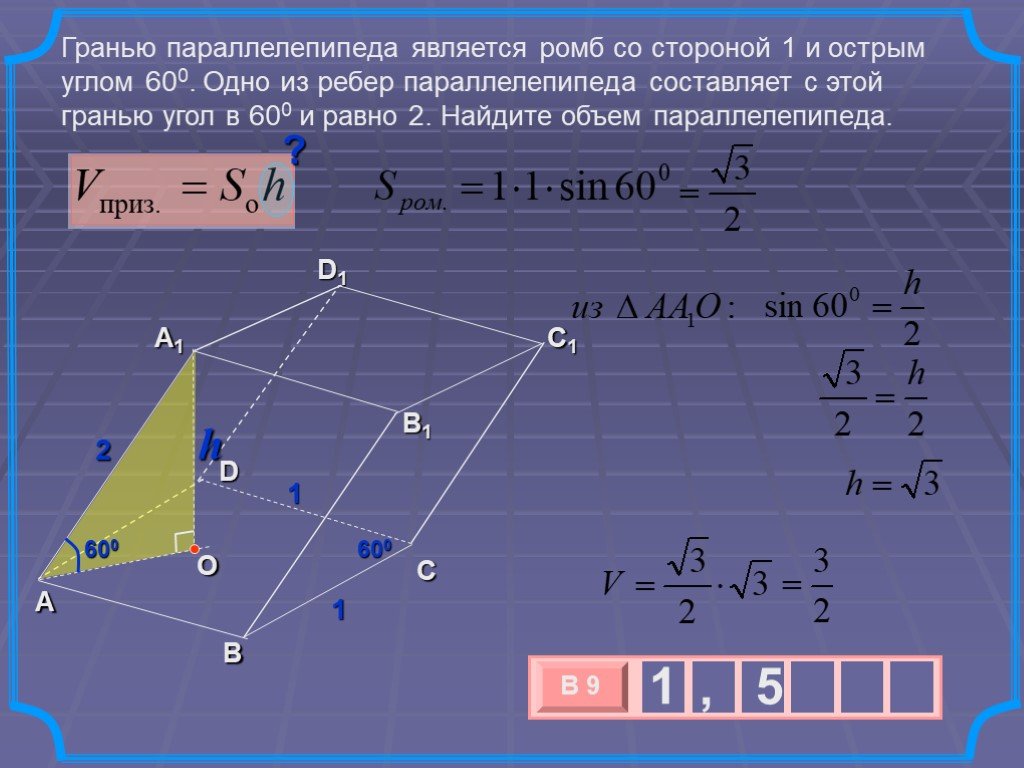
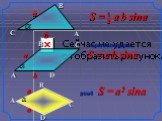
Тело, ограниченное цилиндрической поверхностью и двумя кругами, называется цилиндром. Цилиндрическая поверхность называется боковой поверхностью цилиндра. ...Объём наклонной призмы
Равные тела имеют равные объемы. Если тела А , В, С имеют равные размеры, то что можно сказать об объемах этих тел? Если тело разбито на части, являющиеся ...Цилиндр
Геометрия 11 класс Тема: Цилиндр. Теоретический материал Задачи. Тема: Цилиндр. 1.Примеры цилиндров. 2.Понятие цилиндрической поверхности. 1 2 3. ...Объём тела
ρ масса плотность кг с время t m м/с путь скорость инерция v км/ч год г м мин s. . . . . . Архимед. Архиме́д (Ἀρχιμήδης; 287 до н. э.) — 212 до н. ...Цилиндр
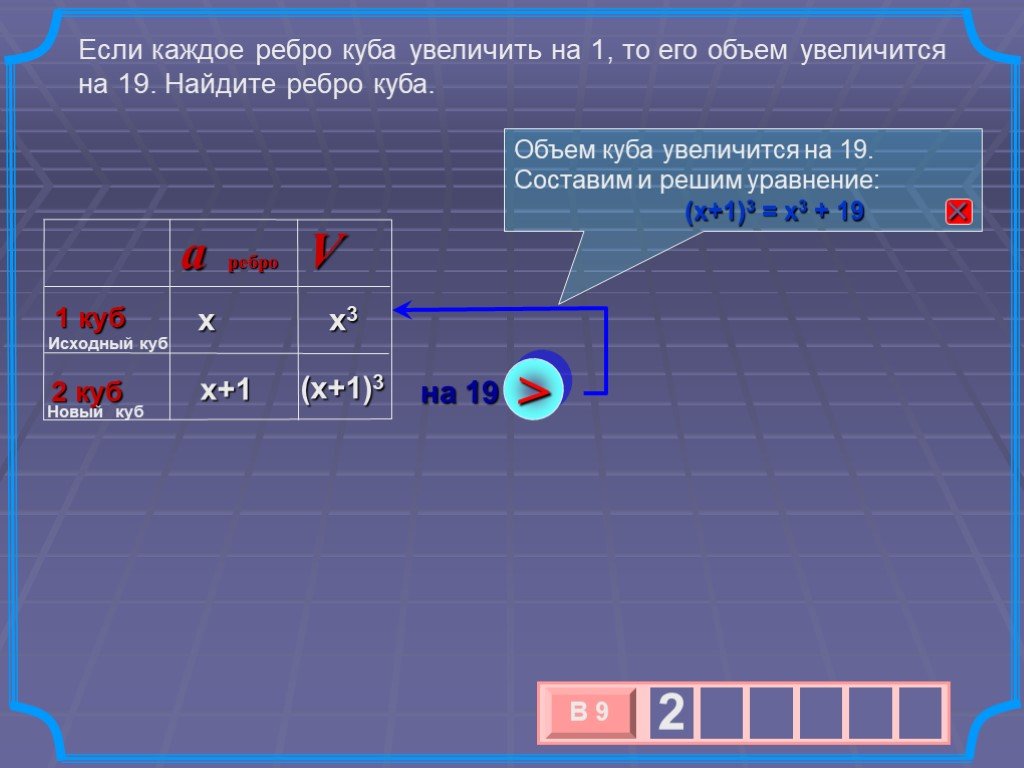
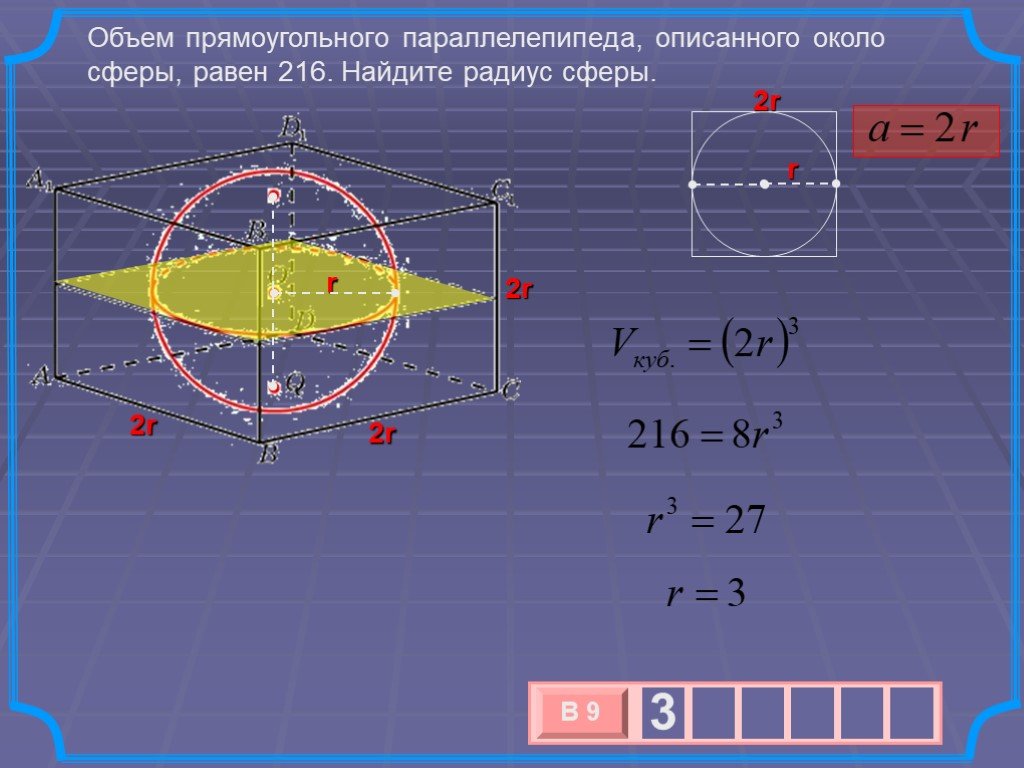
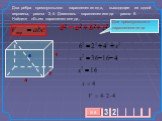
Цили́ндр (греч. kýlindros, валик, каток) - геометрическое тело, ограниченное цилиндрической поверхностью (называемой боковой поверхностью цилиндра) ...Объём прямоугольного параллелепипеда
Блиц-Опрос. Прямоугольный параллелепипед – это (плоская, объёмная) фигура. Стороны граней параллелепипеда называются _______________. У параллелепипеда ...Объём тел
Пусть тело Т, объем которого надо вычислить, заключено между двумя параллельными плоскостями α и β. Введем систему координат – ось ох перпендикулярна ...Объём прямоугольного параллелепипеда
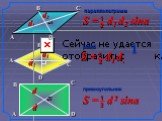
. «Дорогой Хагрид! Оставляю под Вашим присмотром этого дракончика, для которого срочно придётся приобрести аквариум, так как на суше его можно держать ...Объём призмы
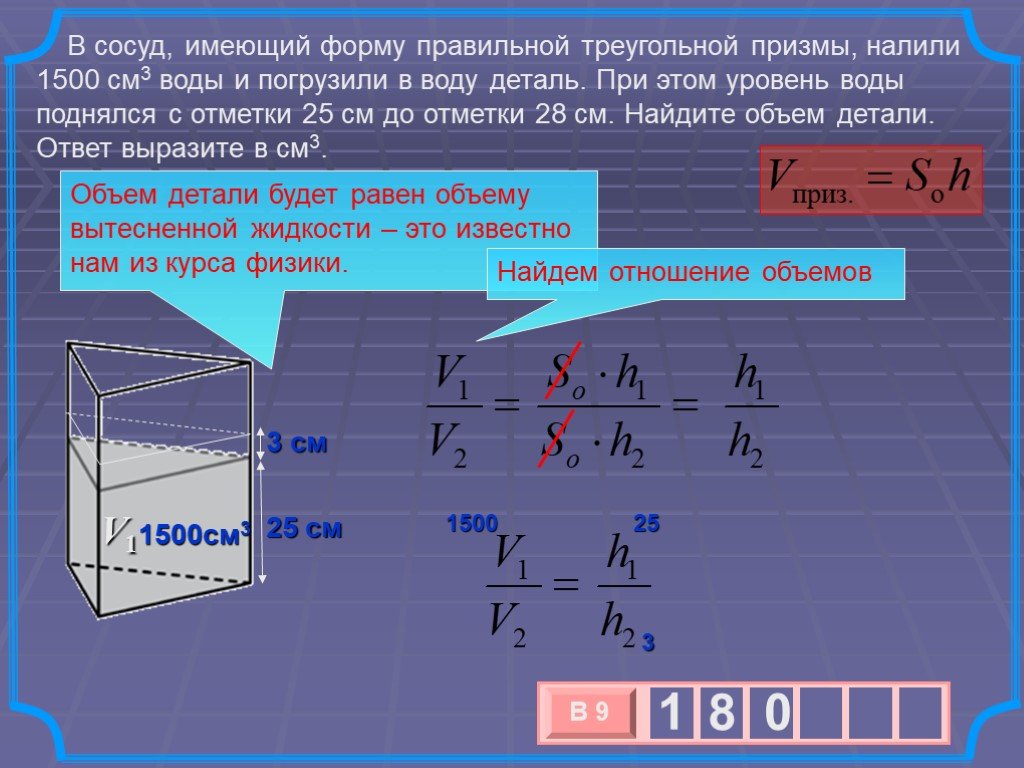
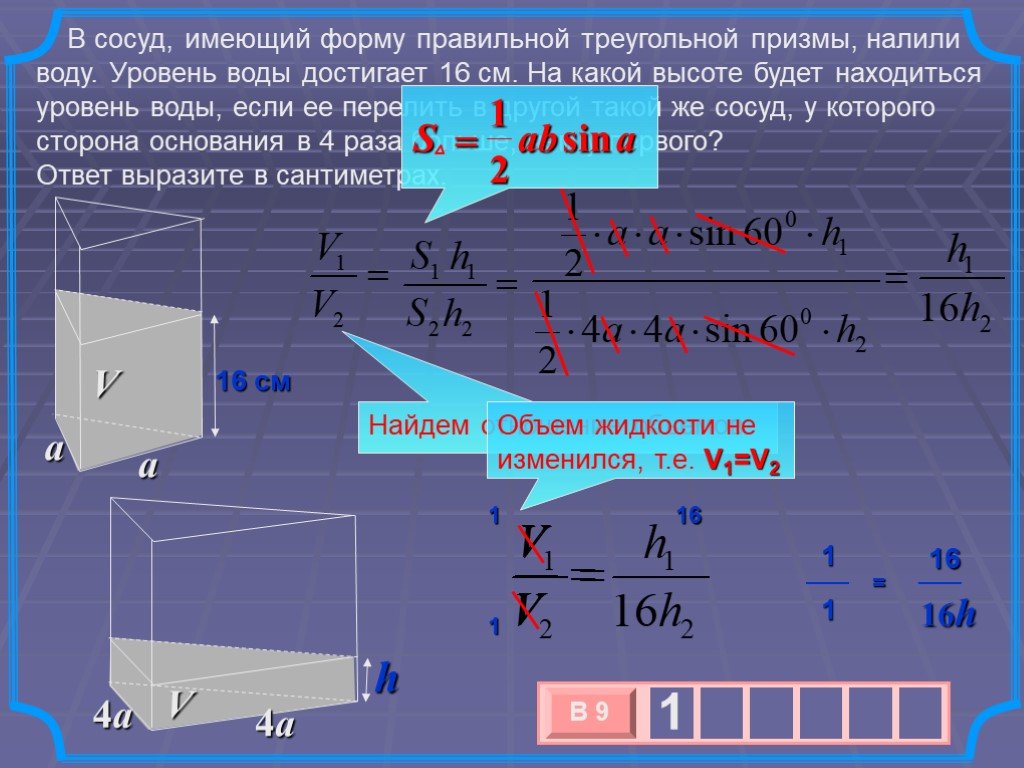
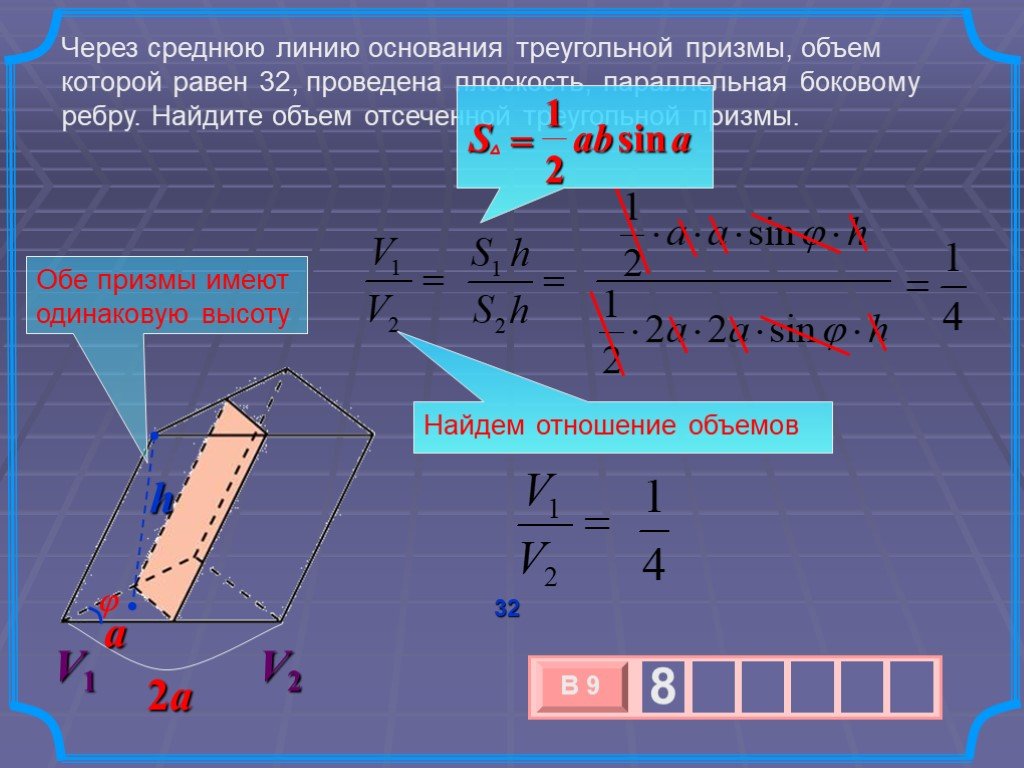
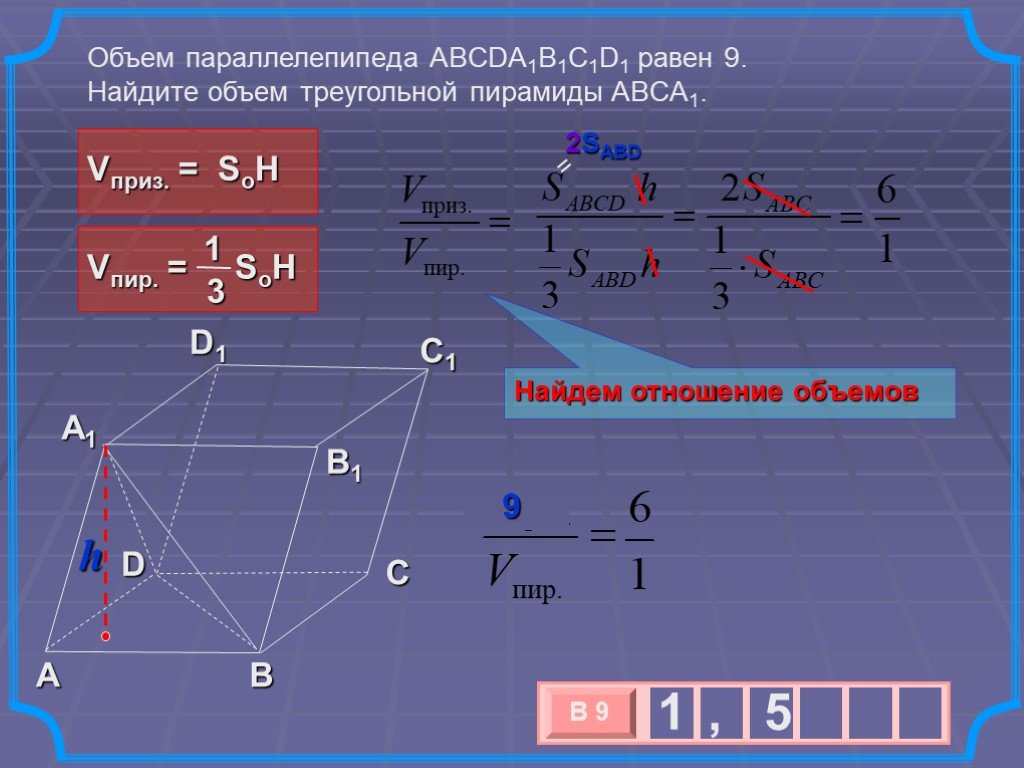
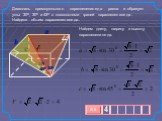
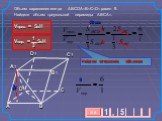
ОБЪЁМ ПРИЗМЫ. ПЛАН ТЕМЫ: I. Понятие объема. II. Основные свойства объёмов. III. Объём произвольной призмы. Объем каждого тела выражается положительным ...Объём пирамиды
ВСПОМНИТЬ, ЧТО ТАКОЕ ПИРАМИДА НАУЧИТЬСЯ ПОЛЬЗОВАТЬСЯ ФОРМУЛОЙ НАХОЖДЕНИЯ ОБЪЁМА ПИРАМИДЫ. Цель работы:. ЧТО ТАКОЕ ПИРАМИДА ТЕОРЕМА ДОКАЗАТЕЛЬСТВО ...Тела вращения. Цилиндр
о. Длина окружности: C=2πr. Площадь круга: r d Окружность и круг. Как получить цилиндр из прямоугольника. Прямой круговой цилиндр- это тело, получаемое ...Цилиндр
Определение цилиндра. Цилиндром называется тело, которое состоит из двух кругов , не лежащих в одной плоскости и совмещаемых параллельным переносом, ...Конспекты
Цилиндр, конус. Решение задач
Муниципальное бюджетное образовательное учреждение. «Гимназия № 7». г. Норильска Красноярского края. Урок математики по ...Цилиндр, его определение, элементы и их свойства
Урок в 11 классе по учебнику «Геометрия 10-11» А. В. Погорелова,. пункт 52-54 год издания 2008-2012. . Тема: «. Цилиндр, его определение, элементы ...Цилиндр, его элементы
Тема урока: Цилиндр, его элементы. . . Цель урока:. . . закрепление у учащихся знаний о теле вращения – цилиндре ( элементы цилиндра, формулы ...Цилиндр
Урок по геометрии на тему: «Цилиндр». 11 класс. Цели. Познакомить учащихся с новыми понятиями: цилиндрическая поверхность, цилиндр, основания ...Цилиндр
Тема урока: «Цилиндр». Автор: Попович Наталия Викторовна. учитель математики. Гимназия №56. Санкт-Петербург. Методическая основа –. планирование, ...Объёмы. Объём прямоугольного параллелепипеда
Урок математики в 5 классе. Подклетнева И.В.( МОБУ Гимназия №15 г. Сочи),Боклаг В.Н. (МОБУ СОШ №10 г. Сочи). . Урок математики в 5 классе. Подклетнева ...Тела вращения. Цилиндр
Урок геометрии в 11 классе. Тема «. Тела вращения. Цилиндр. ». ФИО (полностью). . Козлова Лидия Николаевна. . . Место работы. . ...Объём прямоугольного параллелепипеда
Объём прямоугольного параллелепипеда. Цель:. Обобщить, повторить и систематизировать знания по теме: «Объём. Объем прямоугольного параллелепипеда». ...Объём прямоугольного параллелепипеда
Предмет:. математика. Класс:. 5. Учитель. : Булатова Анна Васильевна. Базовый учебник:. Муравин Г. К., Муравина О. В. «Математика»,5 класс. ...Объём прямоугольного параллелепипеда
МБОУ Белоберезковская СОШ №1 Трубчевского района Брянской области. Урок по теме «Объём прямоугольного параллелепипеда». 5-й класс. Ананченко ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:9 июня 2019
Категория:Математика
Содержит:24 слайд(ов)
Поделись с друзьями:
Скачать презентацию