Конспект урока «Цилиндр, его определение, элементы и их свойства» по математике для 11 класса




































 Урок в 11 классе по учебнику «Геометрия 10-11» А. В. Погорелова, пункт 52-54 год издания 2008-2012
Урок в 11 классе по учебнику «Геометрия 10-11» А. В. Погорелова, пункт 52-54 год издания 2008-2012
Тема: «Цилиндр, его определение, элементы и их свойства»
Урок разработан в рамках образовательной технологии критического мышления.
| I стадия | II стадия | III стадия | IV стадия |
| Вызов (интрига) - актуализация имеющихся знаний; - пробуждение интереса к получению новой информации; - постановка учеником собственных целей обучения | Осмысление содержания - получение новой информации; - корректировка учеником поставленных целей обучения | Практическая деятельность - выполнение в группах поставленных задач и заданий - выводы по итогам выполнения заданий | Рефлексия - размышление, рождение нового знания; - постановка учеником новых целей обучения |
Цель (развивающая): формирование учебно – познавательных компетенций на уроке геометрии через развитие критического мышления для подготовки конкурентоспособной личности.
Цель (учебная): изучить определение цилиндра (кругового, прямого кругового) и связанных с ним понятий; рассмотреть основные виды сечений цилиндра; определить условия существования комбинаций призмы и цилиндра.
Задачи:
-
Формирование навыков критического мышления и исследовательских навыков при изучении нового материала и решении задач;
-
Развивать готовность самостоятельного поиска информации;
-
Создание психологически комфортной среды на уроке;
-
Формирование новых понятий и знаний по теме урока;
-
Формирование навыка применения новых знаний при решении задач;
-
Формирование самооценки.
Вопросы для изучения:
-
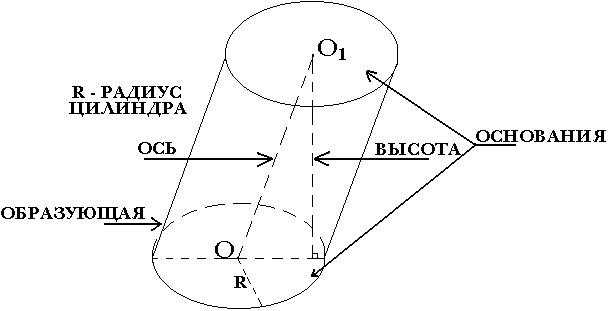
Цилиндр, его основания, образующие и их свойства
-
Виды цилиндра и его поверхность
-
Радиус и высота, ось цилиндра
-
Сечения цилиндра плоскостями
-
Вписанная и описанная призма. Комбинация тел: призма и цилиндра, пирамида и цилиндр
-
Решение базовых задач
Ключевые слова: цилиндр, образующая, основание, высота, радиус, ось, поверхность, сечения плоскостью, вписанная призма, касательная плоскость, описанная призма.
Оборудование: проектор; документ камера, модели цилиндра (прямой и наклонный) и наборы призм, ножницы; карточки с названиями групп: «Исследователи», «Аналитики», «Художники»; карточки с заданиями (формулировки заданий и конверты с карточками – консультантами, карточки с ответами для самопроверки); таблица З-Х-У, тетради на печатной основе.
Подготовительная работа.
Домашнее подготовительное задание для «Исследователей»:
-
Разработать экскурсию по посёлку Иловля, с посещением и просмотром мест, имеющих цилиндрические формы. Подготовить проект-презентацию заочной экскурсии
-
Используя интернет - ресурсы, дополнительную литературу, создать презентацию «Цилиндр» в соответствии с материалом учебника, пункт 52 - 53, результаты представить на уроке
Задание на уроке для «Исследователей»:
| Работа с задачами | |
| Просмотрев и прослушав экскурсию по р. п. Иловля, презентацию «Цилиндр», заполнить первые две части таблицы «З-Х-У». Сформулировать цель своей работы в группе для реализации поставленных задач | |
|
|
Задание на уроке для «Аналитиков»:
-
Просмотрев и прослушав экскурсию по р. п. Иловля, презентацию «Цилиндр», заполнить первые две части таблицы «З-Х-У». Сформулировать цель своей работы в группе для реализации поставленных задач
-
Выполнить тест № 7, вариант № 1-2, задача № 1 в тетради на печатной основе
-
Сделать вывод о правильности высказываний
-
Составить опорный конспект на основании содержания учебника п. 52-54 и информации, полученной из презентации «Цилиндр»
Задание на уроке для «Художников»:
-
Просмотрев и прослушав экскурсию по р. п. Иловля, презентацию «Цилиндр», заполнить первые две части таблицы «З-Х-У». Сформулировать цель своей работы в группе для реализации поставленных задач
-
Нарисовать тела вращения, образованные вращением плоских фигур, изображенных на рисунке.
-
Сделать вывод в соответствии с поставленной целью
-
Составить опорный конспект на основании содержания учебника п. 52-54 и информации, полученной из презентации «Цилиндр», выделив «главные мысли» цветом.
Карточка-консультант для исследователей.
Цель работы:
-
изучить условие возможности вписать призму и пирамиду в цилиндр и описать призму и пирамиду около цилиндра.
-
Научиться применять знания о цилиндре при решении задач. Сформулировать «темы» задач
Необходимые и достаточные условия взаимных комбинаций многогранников и цилиндра:
-
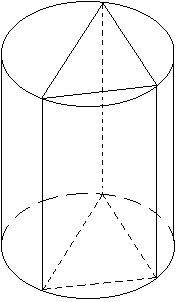
Для того чтобы призму вписать в цилиндр, необходимо и достаточно, чтобы основание призмы было вписанным в окружность плоским многоугольником, где окружность является границей круга, служащим основанием цилиндра, а боковые ребра призмы совмещались с образующими цилиндра. Чтобы пирамида была вписана в цилиндр необходимо и достаточно, чтобы её основание было вписано в основание цилиндра, а вершина совпала с центром верхнего основания цилиндра.
-
Чтобы призма была описана около цилиндра, её основание должно являться многоугольником, описанным около окружности, которая ограничивает основание цилиндра. При этом боковые грани призмы должны касаться образующих цилиндра. Чтобы вписать цилиндр в пирамиду, необходимо и достаточно, чтобы его нижнее основание было вписано в основание пирамиды, а верхнее основание касалось боковых граней пирамиды.
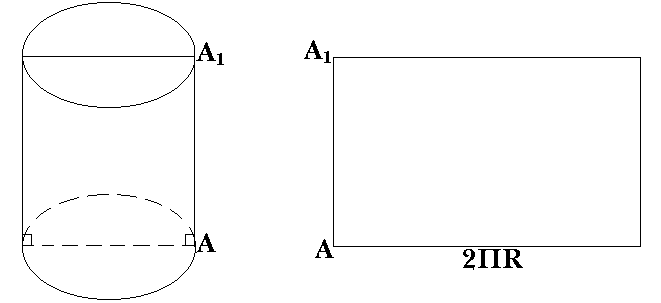
Развертка цилиндра:
Развертка цилиндра выглядит следующим образом:
Формулы для вычисления боковой и полной поверхности: S б.п.=2ПRh, где h-высота, S=ПR2 – площадь круга, S п.п.=2ПR(R+h).
Решение задачи № 2.
Диагональ, высота и диаметр цилиндра (удвоенный радиус) образуют треугольник ACD, угол D = 90О; по теореме Пифагора
АС2 = AD2 + CD2 , следовательно CD2 = АС2 - AD2, то есть CD2 = 7,52- 62, откуда следует, что высота цилиндра равна 4,5. Ответ 2.
Решение задачи № 3
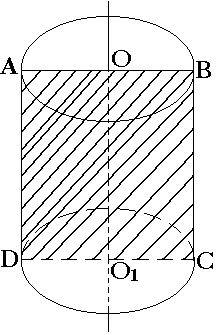
Сечение параллельное оси цилиндра есть прямоугольник AВCD и его площадь находится, как произведение длины и ширины. Если AВ=12 и S=48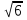 , то ВC= S: AВ, то есть 48
, то ВC= S: AВ, то есть 48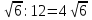 .
.
Рассмотрим треугольник ВСО1: он равнобедренный, так как его боковые стороны образованы радиусами цилиндра. Расстояние от оси цилиндра до секущей плоскости - это длина перпендикуляра, опущенного из точки О1 на сторону ВС. Так как треугольник равнобедренный, конец перпендикуляра делит основание пополам.
По теореме Пифагора расстояние равно 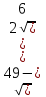 =
=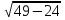 =5. Ответ 1.
=5. Ответ 1.
Вывод: для решения задач с цилиндром, необходимо правильно строить чертёж и применять знания, полученные в планиметрии.
Карточка-консультант для аналитиков.
Цель работы:
-
Применить знания о цилиндре (определение), его элементах и их свойствах, сечениях и поверхности для проверки правильности или неправильности утверждений
-
Научиться составлять опорные конспекты и ставить цель работы
Тест № 7, вариант № 1, задача № 1
Вывод: неверным является утверждение «5)». Остальные утверждения верны, так как подтверждают теоретические знания.
Тест № 7, вариант № 2, задача № 1
Вывод: неверным является утверждение «4)». Остальные утверждения верны, так как подтверждают теоретические знания.
Карточка-консультант для художников.
Цель работы: Изобразить тела вращения, образованные вращением плоских фигур, изображенных на рисунках.
| | |
| | |
Цель работы: Составить опорный конспект по теме «Цилиндр», отобразив в нем знания, приобретенные на уроке.
| Цилиндр-это фигура, состоящая из двух кругов, совмещаемых параллельным переносом и всех отрезков, соединяющих соответствующие точки этих кругов. Свойства: 1. Основания равны и параллельны (из опр.). 2. Образующие равны и параллельны (из свойств параллельного переноса, по свойству параллельных плоскостей). | |||||
| | Цилиндр называется прямым, если образующие перпендикулярны основанию. В прямом цилиндре: ось=высота=образующая. | | Прямой цилиндр наглядно можно представить как тело, которое описывает прямоугольник при вращении его около стороны как оси. | ||
| сечения | |||||
| прямоугольник | осевое | | |||
| Призма называется вписанной в цилиндр, если основание её равные многоугольники, вписанные в основание цилиндра, а боковые рёбра являются образующими цилиндра. | Призма называется описанной около цилиндра, если основание её - это многоугольники описанные около основания цилиндра, а боковые грани касаются цилиндра. | Боковая поверхность цилиндра: L-длина круга L=2ПR S боковой поверхности=L h, где h-высота, S б.п.=2ПRh Площадь полной поверхности цилиндра - это сумма площадей боковой поверхности и двух оснований (S=ПR2). S п.п.=2ПR(R+h). | |||
Ход урока
I часть. Создание психологического настроя: вызов - интрига
Прежде, чем объявить тему урока, предлагаю совершить заочную экскурсию по родному поселку, подготовленную ученицами нашего класса.
1. Заочная экскурсия по р. п. Иловля. Слайд - шоу с комментариями
|
| |
| Проезжая мимо КНС иногда можно увидеть ярко оранжевого цвета специализированную машину. Если она стоит на месте, значит, в поселке все в полном порядке и все работает как часы. |
|
| Попав в центр посёлка, наше внимание привлекает фасад здания городской аптеки. Её необычная геометрия – закруглённость центральной части крыши и фасада стала решающим моментом при выборе маршрута нашей необычной экскурсии. |
|
| Проезжая мимо Иловлинского отделения сбербанка, на его заднем дворе можно увидеть небольшие строения круглой формы. Это воздуховоды подвальных помещений сбербанка. Строения такой формы имеет самое прямое отношение к теме сегодняшнего урока. |
|
| Если вы покидаете наш поселок на автобусе, то ваш путь лежит на автостанцию. Её посадочная площадка защитит вас от дождя и непогоды, так как навес укреплён на целом ряде опор правильной цилиндрической формы |
|
| Остановившись на переезде, не забудьте посмотреть налево. Там располагаются помещения складов и хранилищ. Одно из них – ангар полуцилиндрической формы. |
|
2. Дополнение слайдами учителя: Чтобы перейти к теме урока, я предлагаю «посетить ещё одно памятное место.
|
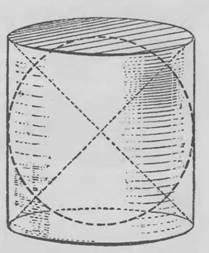
| Предание гласит, что Архимед завещал вырезать на своем надгробном памятнике рисунок, сделанный его собственной рукой. По завещанию мыслителя, математика, физика на могильном камне был вырезали символ его геометрического открытия, которым он очень гордился: Цилиндр, описанный вокруг шара. |
| ||
| Другой великий ученый математик, механик, физик, философ; по происхождению швейцар, но прожил половину жизни в России, захоронен в Петербурге, полное собрание сочинений которого не умещается в 60 больших томах. Уже будучи слепым он написал математические работы, связанные с исследованиями поверхностей, которые можно развернуть на плоскости и о их кривизне. Одна из поверхностей – цилиндр. |
| |||
| -Вот и мы сегодня попытаемся понять красоту тела вращения Цилиндра, предлагаю построить изучение по следующим вопросам:
Как будет сформулирована цель урока? Учащиеся формулируют учебную цель. Учитель добавляет цель воспитательную и задачи урока. | ||||
II часть Осмысление содержания
Изучение новой темы строится в соответствии с презентацией, подготовленной учениками группы «Исследователей». Остальные группы учащихся, просматривая презентацию с комментариями авторов, работают с таблицей «З-Х-У»
| Цилиндры бывают прямыми и наклонными в зависимости от того перпендикулярны или наклонны плоскости оснований к образующим. |
Радиус R цилиндра | |
| Цилиндром называется тело, которое состоит из двух кругов , не лежащих в одной плоскости и совмещаемых параллельным переносом, и всех отрезков, соединяющих соответствующие точки этих кругов. | Радиусом цилиндра называется радиус его основания. Высотой цилиндра называется расстояние между плоскостями его оснований. Осью цилиндра называется прямая, проходящая через центры оснований. | 6. Основания равны и параллельны Все образующие цилиндра параллельны и равны друг другу |
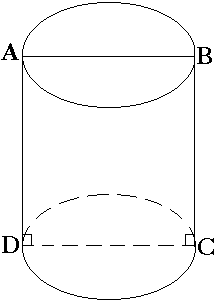
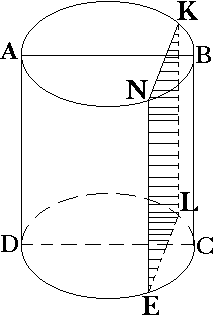
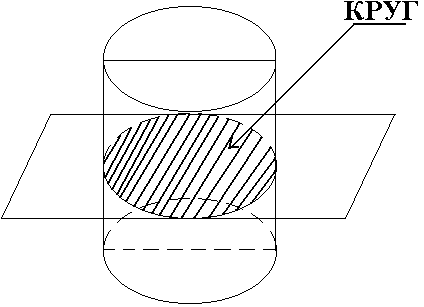
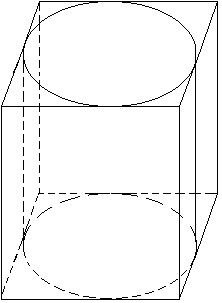
| Сечение цилиндра плоскостью, параллельной его оси ─ прямоугольник. Сечение цилиндра, проходящее через ось цилиндра называется осевым сечением и , так же является прямоугольником. | Плоскость, параллельная плоскости основания цилиндра, пересекает его боковую поверхность по окружности, равной окружности основания. | Сечения, которые проходят под углом к основанию прямого цилиндра являются фигурами неправильной формы - эллипсы. |
| Касательной плоскостью к цилиндру называется плоскость, проходящая через образующую цилиндра и перпендикулярная плоскости осевого сечения, содержащей эту образующую | |
|
III часть Практическая деятельность
-
Работа в группах над проблемами, обозначенными в карточках с заданиями. Если возникают трудности, можно воспользоваться конвертом с карточкой-консультантом.
-
Решение задачи о нахождении полной поверхности цилиндра после выступления группы исследователей с разверткой и формулой полной поверхности.
«Найти площадь полной поверхности цилиндра, полученного при вращении прямоугольника со стороной 6 см и диагональю 10 см вокруг меньшей стороны».
Чертеж выполнить в тетради и спроектировать на доску через документ камеру.
Проблема может возникнуть, если учащиеся забыли формулу площади круга и длины окружности.
IV часть Рефлексия. Выводы и подведение итогов
-
Краткая информация (через документ камеру) от каждой группы о результатах решения поставленных проблем. Итоги работы с таблицей «З-Х-У». Приложение № 1
-
Выставление оценок
-
Сравните содержимое ваших таблиц « З-Х-У», вопросов для изучения и вопросов, которые возникли при решении задач: может, остались какие-либо неразрешенные проблемы. Вопрос о нахождении поверхности цилиндра, формулы длины окружности и площади круга. Условие вписанной и описанной призмы.
-
Задание на дом
Дома обязательно просмотрите таблицу, обозначить вопросы требующие дополнительной работы; п.52-54 (п. 181-183 по старым учебникам), контрольные вопросы 1-5; задача №1, 7 – разобрать по учебнику, для желающих № 6, особенно название частного вида цилиндра.
-
Рефлексия по психологическому состоянию учащихся и проведенному уроку.
Составьте синквейн по теме «Цилиндр».
Спасибо за урок. До свидания
Здесь представлен конспект к уроку на тему «Цилиндр, его определение, элементы и их свойства», который Вы можете бесплатно скачать на нашем сайте. Предмет конспекта: Математика (11 класс). Также здесь Вы можете найти дополнительные учебные материалы и презентации по данной теме, используя которые, Вы сможете еще больше заинтересовать аудиторию и преподнести еще больше полезной информации.