Презентация "Методы решений заданий С5. Метод областей в решении задач" по математике – проект, доклад
Презентацию на тему "Методы решений заданий С5. Метод областей в решении задач" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 11 слайд(ов).
Слайды презентации
Список похожих презентаций
Аксиомы стереометрии и их следствия. Решение задач
Цель урока: обобщение и применение аксиом и их следствий к решению задач. Математический диктант. 1). Сформулируйте аксиомы стереометрии: Аксиома ...Арифметическая и геометрическая прогрессии при решении задач
с и п о г р я е. ПРОГРЕССИЯ. арифметическая аn+1=аn+ d an= a1+d(n-1). геометрическая bn+1= bn * q bn= b1*qn-1. Арифметическая и геометрическая прогрессии ...Алгебра высказываний. Решение логических задач
Задача 1: Составьте сложное высказывание в словесной форме из простых, заданных математическим формулировкам:. Высказывание А: «Учащийся Иванов хорошо ...Алгебраические поверхности в пространстве
Цели и задачи. Цели: Рассмотреть основные понятия по теме «Алгебраические поверхности второго порядка в пространстве» Задачи: Рассмотреть понятие ..."Взаимное расположение прямых в пространстве. Угол между двумя прямыми
«Крупное научное открытие дает решение крупной проблемы, но и в решении любой задачи присутствует крупица открытия». Дьердье Пойа, венгерский математик. ...Биссектриса угла в треугольнике
Задачи УЧЕБНИК А О В С D 80º ? 180º- 80º= 100º 100º Ответ:155º, 25º, 155º. Задача №535 биссектриса ? Определение. Биссектриса угла – это луч с началом ...Бинарный урок геометрии и информатики "Четырехугольники. Решение задач" Лауреат
Проверка домашнего задания. В трапеции АВСD (АD – большее основание) диагональ АС ┴СD и делит ВАD пополам, СDА=60, периметр трапеции – 20 см. Найдите ...Без математики, друзья, в жизни нам никак нельзя
Актуальность. Математика находится в тесной связи со всеми естественными, гуманитарными, точными науками и др., математические знания применяются ..."Смешанные дроби. Представление смешанного числа в виде неправильной дроби".
Смешанные дроби. Представление смешанного числа в виде неправильной дроби. 02.03. Определите координаты точек А, В, С и М. ...Арифметическая и геометрическая прогрессии в заданиях ГИА
Цели урока: Обобщить и систематизировать знания учащихся по данной теме. Разобрать типичные задания встречающихся в сборниках для подготовки к ГИА. ...5.Уравнение в полных дифференциалах. Интегрирующий множитель
Теорема:. Для того чтобы дифференцировать выражение , где и определены и непрерывны в области плоскости и имеют в ней непрерывные частные производные ...«Симметрия в пространстве» геометрия
Что такое симметрия? Симметрия в переводе с греческого означает соразмерность. Под симметрией принято понимать свойство геометрической фигуры, расположенной ...«Решение задач с помощью пропорций»
Найти значение Х: Х:3=4:6 5:Х=2:6 7:3=Х:18 Устная работа. Указать вид пропорциональной зависимости:. Какова зависимость пути от времени? Какова зависимость ...«Решение задач по математике»
10 февраля. В классе. Задача условие вопрос решение ответ. Быстро и правильно считать. Правильно записывать решение задачи. Кричать и сердиться, когда ...«Математика в профессиях»
Ознакомление с типами профессий и характеристиками труда. Исследование значения математики в различных областях деятельности человека. Развитие познавательной ...«Закрепление изученого» (Сложение и вычитание с переходом через десяток в пределах 20)
Цели урока:. 1. Закрепить знания о сложении и вычитании с переходом через десяток в приделах 20. 2. Упражняться в решении задач изученных видов. План ...Алгоритм решения задач на пропорции
Эпиграф: «Математика обладает двумя великими сокровищами. Первое-это теорема Пифагора, второе-деление отрезка в крайнем и среднем отношении.» Иоганн ...Алгоритм решения простых задач
. ЗАДАЧА условие Вопрос, задание. Работа в парах. 1. Налетело 5 гусей-лебедей, подхватили и унесли братца Иванушку. 2. Печка испекла девять ржаных ...Арифметическая прогрессия в древности
Египетские папирусы и вавилонские клинописные таблички, относящие ко II тыс. до н.э., содержат примеры задач на арифметическую прогрессию. Каких-либо ...Арифметические действия в двоичной системе счисления
ЗАДАНИЕ «ТЕЗИСЫ». Верно ли каждое из следующих утверждений? Если «Да», то записывайте 1. Если «Нет», то записывайте 0. В результате должно получиться ...Конспекты
Виды уравнений. Методы решения уравнений
ГАОУ НПО Профессиональный лицей № 59. Оренбургская область, Красногвардейский район, с. Плешаново. Виды уравнений. Методы решения уравнений. ...Бородинское сражение в математических задачах
Открытый урок «Бородинское сражение в математических задачах». Карташова Ирина Викторовна , учитель математики МБОУ «Бирюковская СОШ». Техническое ...I признак равенства треугольников в задачах
ТЕМА УРОКА:. I. признак равенства треугольников в задачах. ТИП УРОКА. : закрепление изученного материала. КОНТИНГЕНТ УЧАЩИХСЯ:. 7 класс. ...Виды углов в планиметрии
Лабораторно-практические занятия по геометрии в 7 классе. Лабораторно-практические занятия имеют важное значение, особенно при обучении детей с ...Видеть и слышать, или как не потеряться в мире информации
Конспект – сценарий урока, разработанного учителями МОУ Брызгаловская СОШ Ивановой Е.Б. и Колпаковой Л.В. Тема: «Видеть и слышать, или как не потеряться ...Введение в теорию вероятностей
9 класс. Тема: Введение в теорию вероятностей.(90 мин.). Развитие и образование ни одному человеку не могут быть даны или сообщены. Всякий, ...Большие и малые числа в химии
МКОУ «Средняя общеобразовательная школва №5. . города Ершова Саратовской области». . Бинарный урок. Большие и малые числа в химии. Провели ...Арифметический способ отбора корней в тригонометрических уравнениях
Конспект урока для 11 класса на тему «Арифметический способ отбора корней в тригонометрических уравнениях». Цели и задачи урока:. . . повторение ...+ двухзначных и однозначных чисел в пределах 100
УРОК МАТЕМАТИКИ. Тема:. + двухзначных и однозначных чисел в пределах 100 (урок обобщения). Цель:. Создание условий для формирования УУД при ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:3 июня 2019
Категория:Математика
Содержит:11 слайд(ов)
Поделись с друзьями:
Скачать презентацию




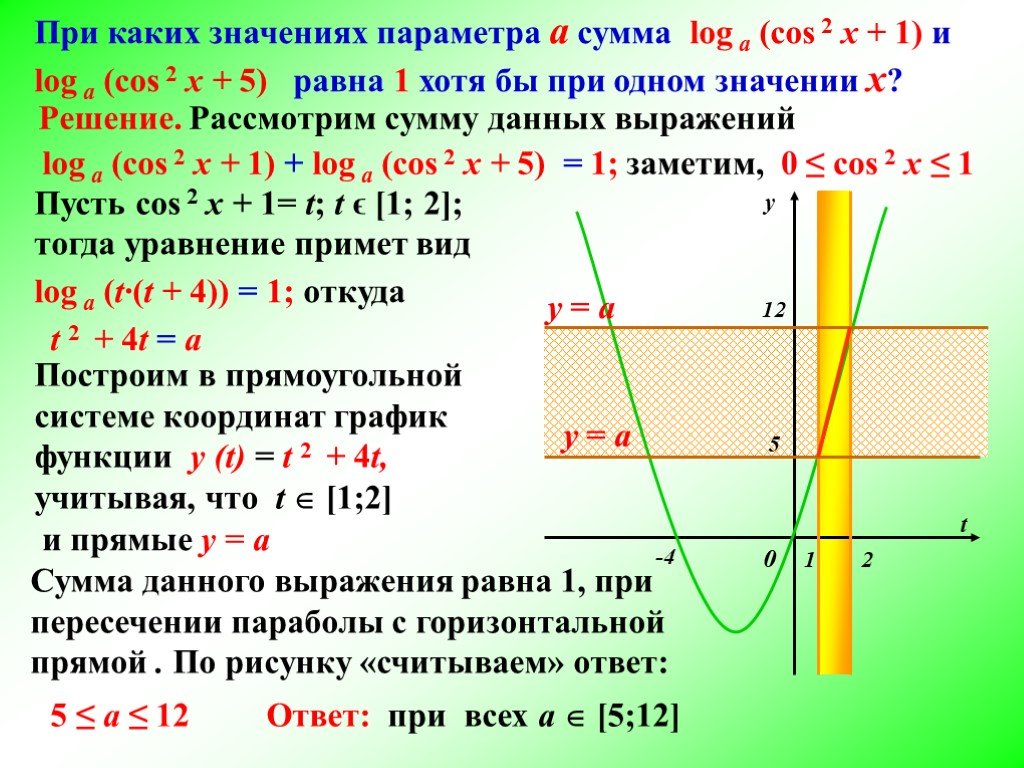





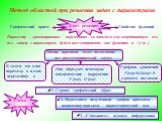


![Решение. Рассмотрим сумму данных выражений. t 12. Сумма данного выражения равна 1, при пересечении параболы с горизонтальной прямой . По рисунку «считываем» ответ: 5 ≤ а ≤ 12. Пусть сos 2 x + 1= t; t ϵ [1; 2]; тогда уравнение примет вид. При каких значениях параметра а сумма log a (cos 2 x + 1) и lo Решение. Рассмотрим сумму данных выражений. t 12. Сумма данного выражения равна 1, при пересечении параболы с горизонтальной прямой . По рисунку «считываем» ответ: 5 ≤ а ≤ 12. Пусть сos 2 x + 1= t; t ϵ [1; 2]; тогда уравнение примет вид. При каких значениях параметра а сумма log a (cos 2 x + 1) и lo](https://prezentacii.org/upload/cloud/19/06/151017/images/thumbs/screen9.jpg)