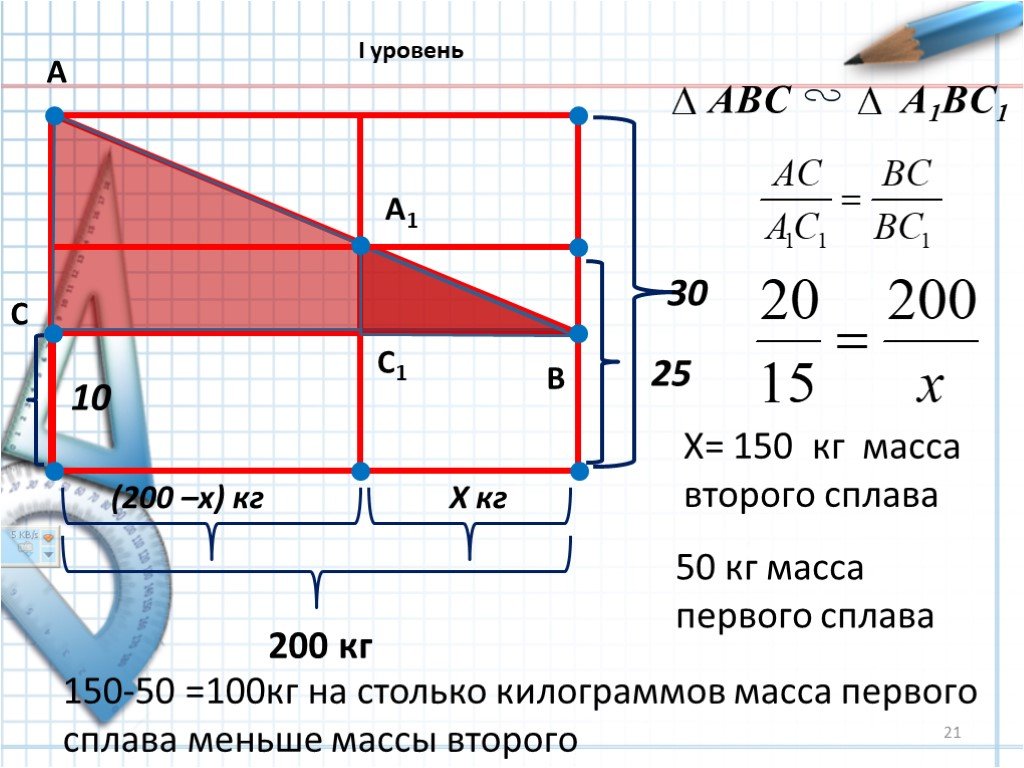
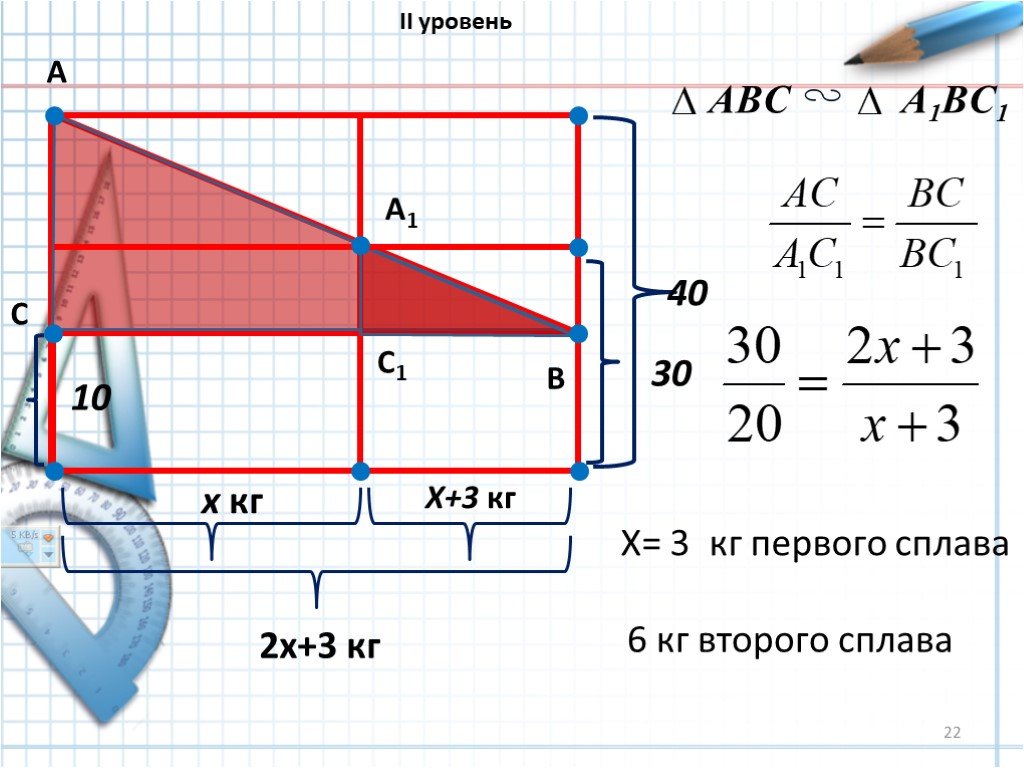
Презентация "Применение двумерных диаграмм" по математике – проект, доклад
Презентацию на тему "Применение двумерных диаграмм" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 24 слайд(ов).
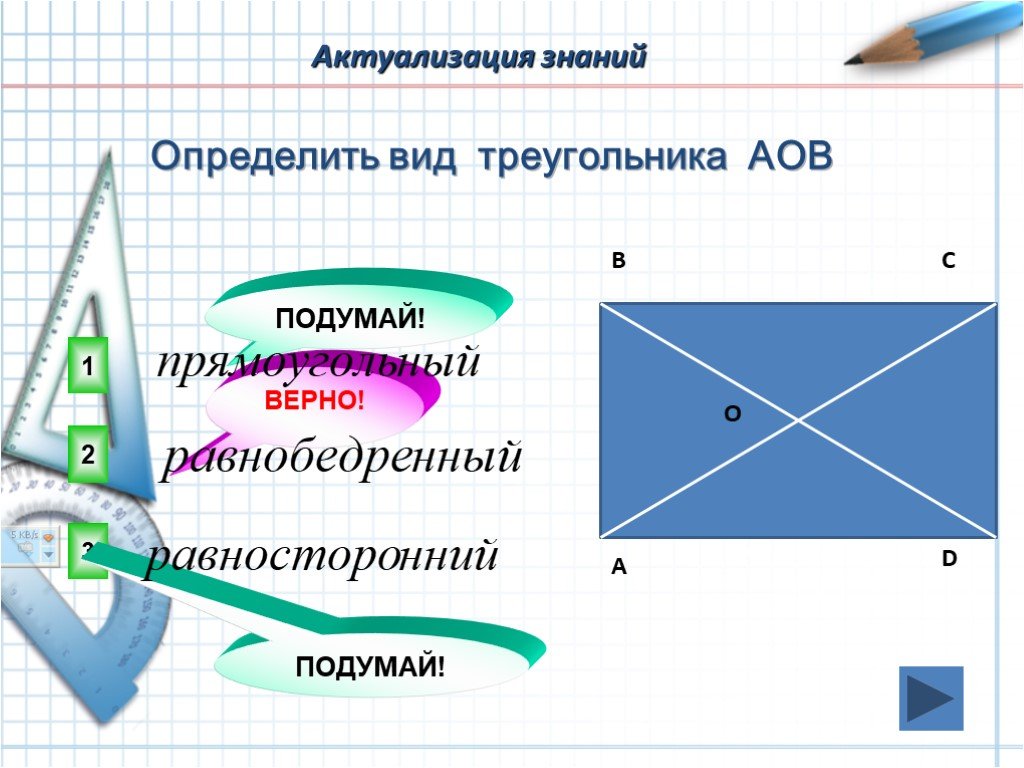
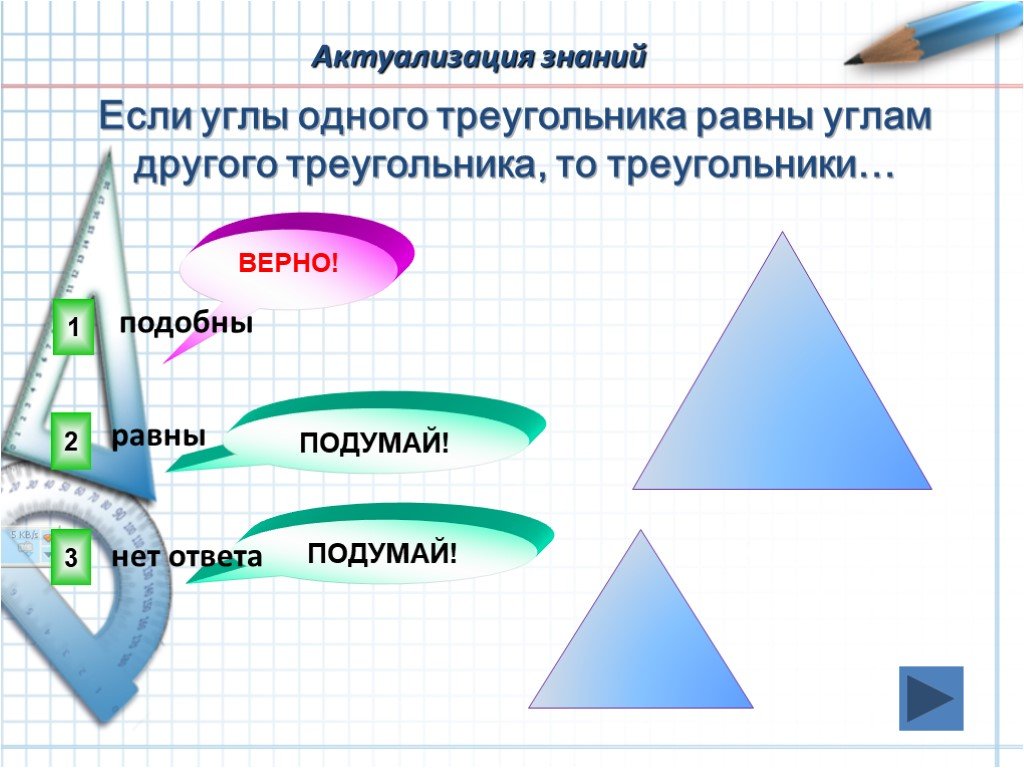
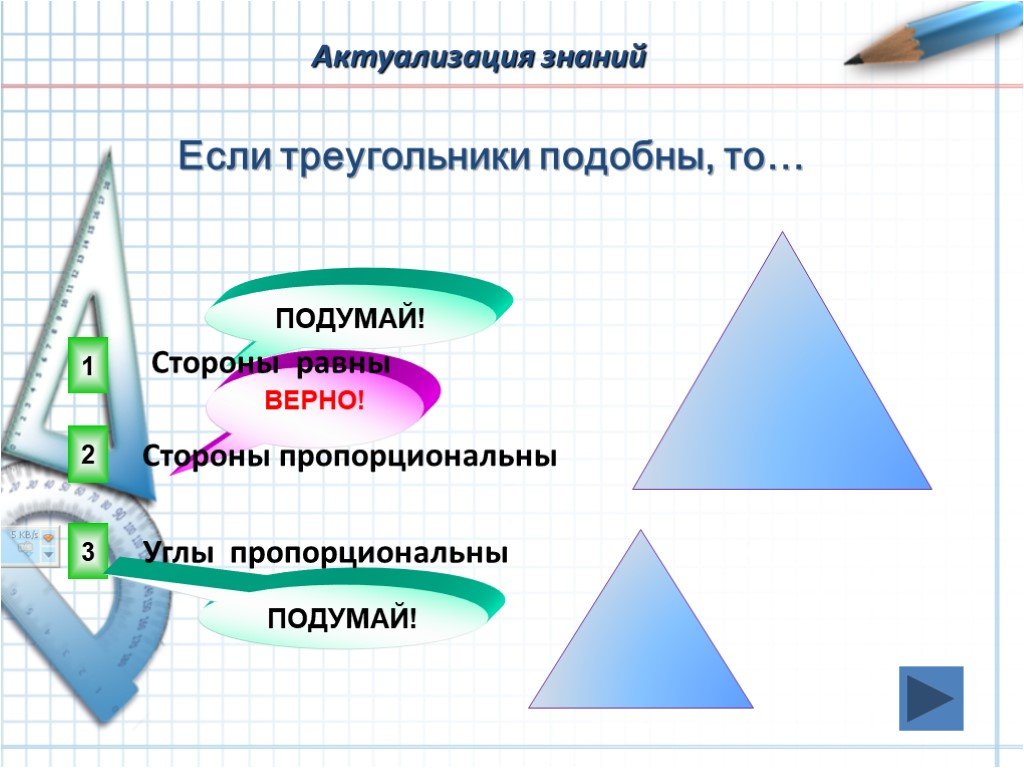
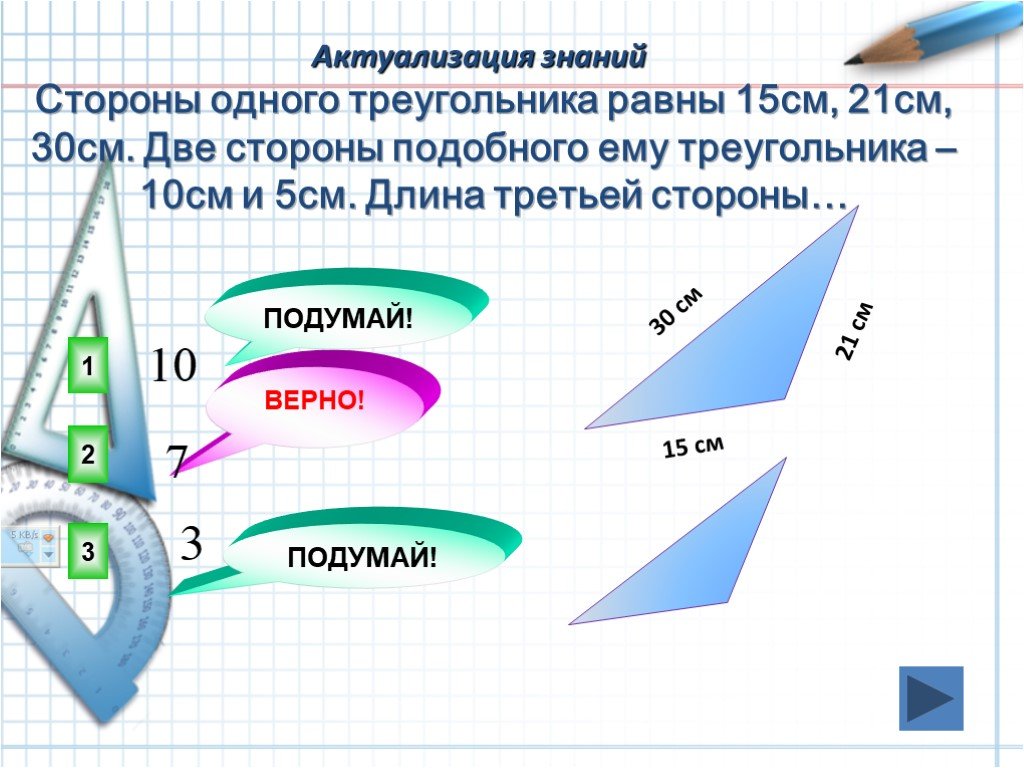
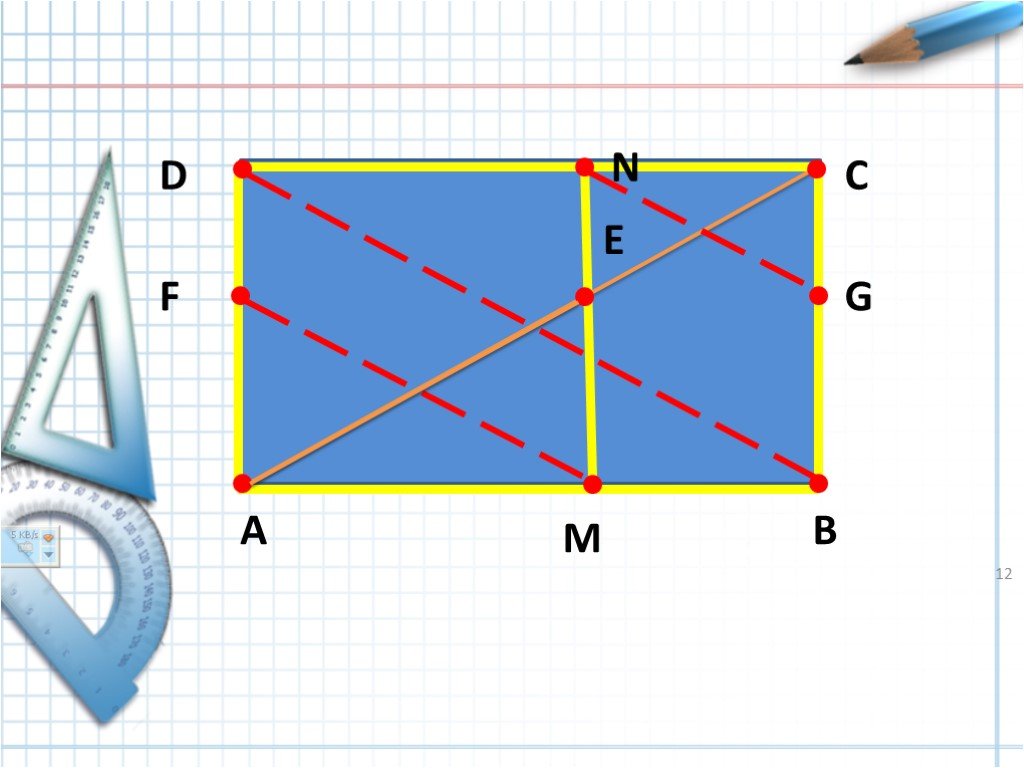
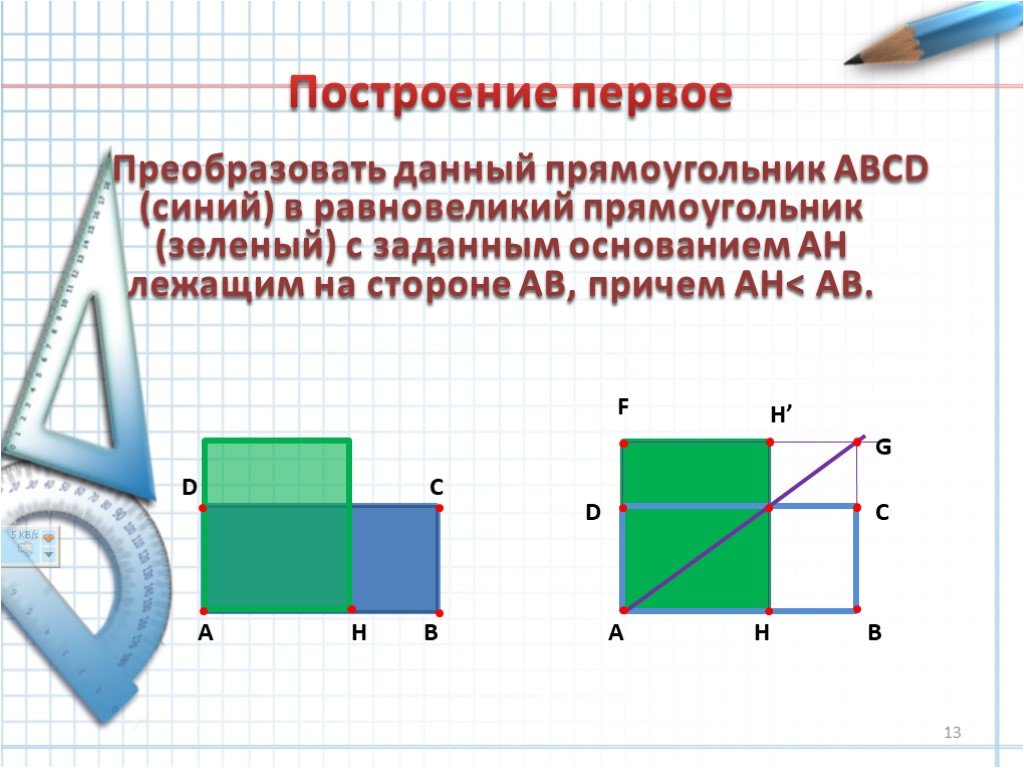
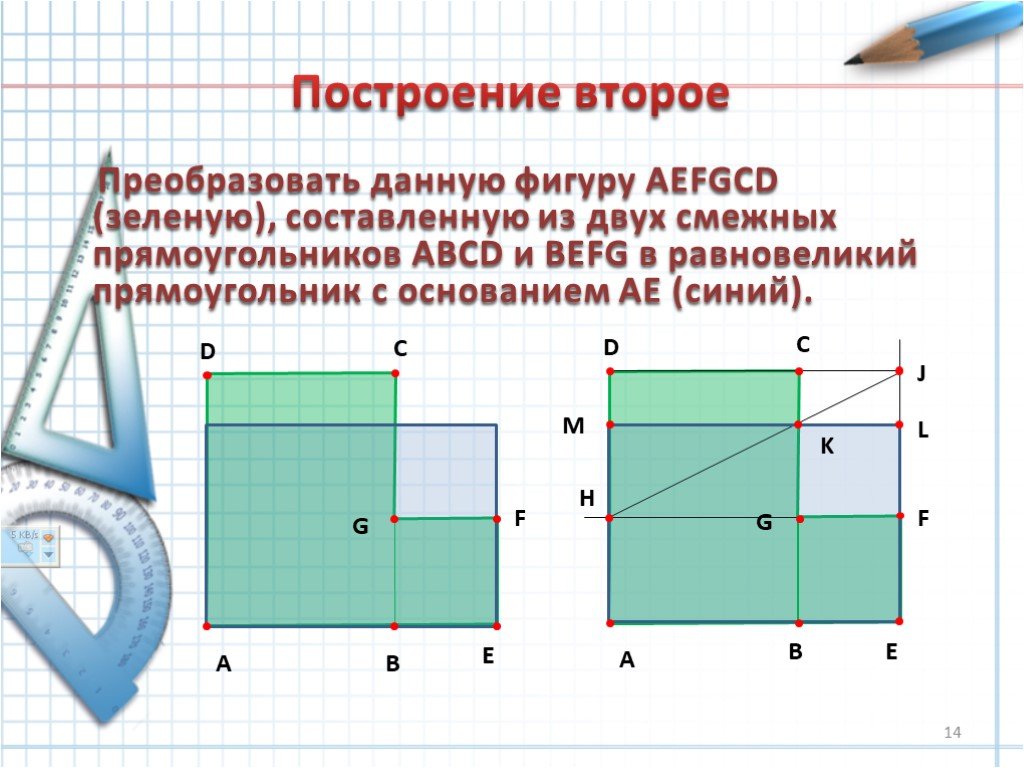
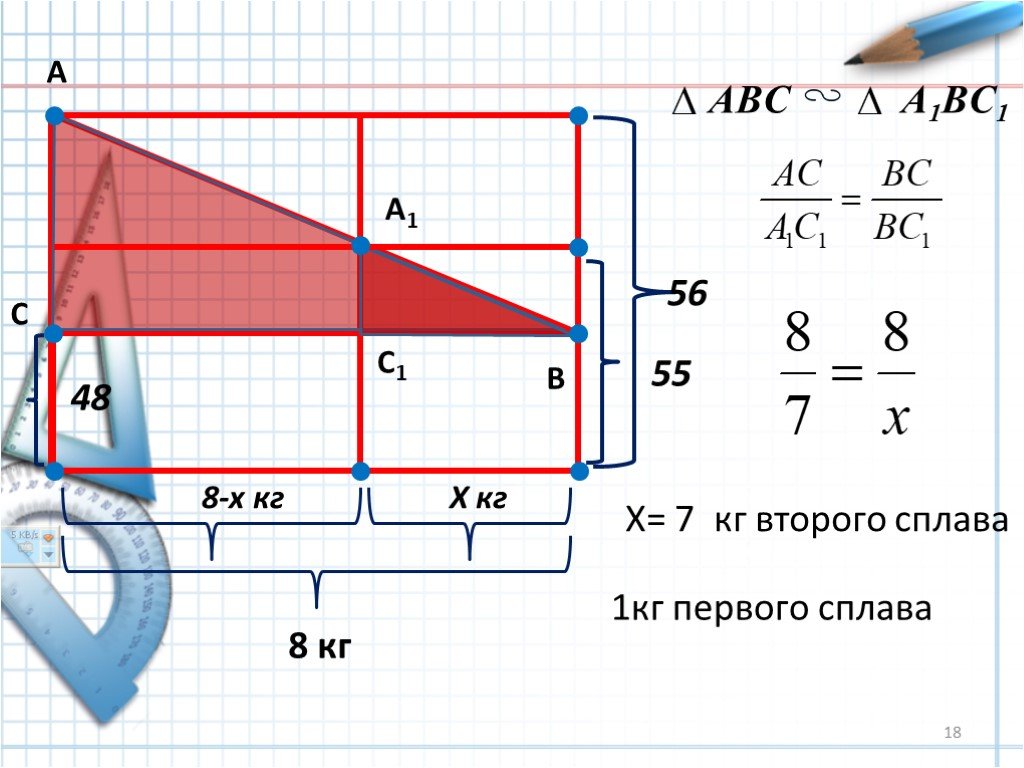
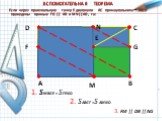
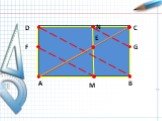
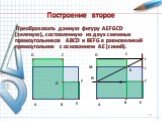
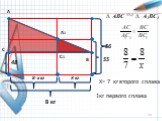
Слайды презентации
Список похожих презентаций
Применение УДЕ на уроках математики
Ключевым упражнением по УДЕ является составление и решение обратных задач. В методике составления и решения взаимообратных задач наиболее ценны не ...Применение элементов математического анализа при решении задач
- Учиться проводить анализ условия задачи, что помогает поиску способа решения;. Цели урока. - Учиться переводить язык задачи на язык производной ...Применение свойств и признаков равенства прямоугольных треугольников к решению практических задач
«Сближение теории с практикой даёт самые благотворные результаты, и не одна только практика от этого выигрывает». П.А. Чебышев. Найдите пары равных ...Применение статистических характеристик для создания портрета учащегося
Тема работы:. Применение статистических характеристик для создания портрета учащегося. научиться применять на практике статистические характеристики ...Применение производной функции
с и л а. в у м е. I вариант II вариант Буква С Буква В. Буква И Буква У. Буква Л Буква М. Буква А Буква Е 7. Сложилась фраза. ...Применение распределительного свойства умножения
Ход урока:. 1. Устные задания. 2. Свойства сложения и умножения. 3. Решение упражнений. 4. Физкультминутка. 5. Самостоятельная работа. 6. Итог урока. ...Применение геометрии
Стол, доска, кусок фанеры – Это плоскости примеры. Из тетради лист положим – Это плоскость будет тоже. *** Если равные в фигурах Две соседних стороны, ...Применение производной к исследованию функции
Применение производной к исследованию функции. Критические точки функции. х у у = g (х) у = f (х). Повторение: описание свойств функции по её графику ...Применение векторов к решению задач
Цели: Показать применение векторов при решении геометрических задач на конкретных примерах; Совершенствовать навыки выполнения действий над векторами. ...Применение вероятностных методов
Применение теории вероятности. Что такое вероятность? «Вероятность – возможность исполнения, осуществимости чего-нибудь». Какое определение дает основатель ...Построение диаграмм и графиков функций
Диаграмма (график) — это наглядное графическое представление числовых данных. Основные типы диаграмм. Линейчатая Круговая Линии (график). показывает ...Построение диаграмм и графиков
Контроль знаний учащихся. Что такое диаграмма и для чего она используеся? Диаграммы – это графическое представление данных. Они используются для анализа ...Построение диаграмм и графиков
Цель урока. Узнать, что такое диаграмма и из каких объектов она состоит. Научиться создавать различные типы диаграмм. Уметь выбирать оптимальные диаграммы ...Применение производной в физике
В математике следует помнить не формулы, а процессы мышления. В.П. Ермаков. Урок № 1 повторительно-обобщающий. Производная и ее применение при решении ...Применение графов в теории вероятностей
Вероятностно – статистическая линия становится сегодня неотъемлемой частью школьного курса математики. Не исключено, что задачи, связанные с вычислением ...Применение производной для исследования функций
Монотонность функции. Убывает на (-;x, x) Возрастает на х1; х2. Постоянна на а;в. у х У=f(x) x1 а в. Исследование функции на возрастание. ...Применение задач линейного программирования в практической деятельности
Если ученик в школе не научился сам ничего творить, то и в жизни он всегда будет только подражать, копировать, так как мало таких, которые бы, научившись ...Применение производной к исследованию функций
Теория без практики мертва или бесплодна, практика без теории невозможна или пагубна. Для теории нужны знания, для практики, сверх всего того, и умение. ...Применение ИКТ для подготовки к ЕГЭ по математике
«Тот, кто не смотрит вперед, оказывается позади» Джордж Герберт. Повышение эффективности работы педагога при подготовке учащихся к сдаче ЕГЭ по математике. ...Применение распределительного свойства умножения
Ход урока. 1. Умножение суммы на число 2. Умножение разности на число 3. Умножение смешанного числа на натуральное 4. Вынесение за скобки общего множителя. ...Конспекты
Сложение 57+40, 40+57. Применение переместительного закона математики
Урок математики. 3 класс. «Сложение 57+40, 40+57. . . Применение переместительного закона математики». 5 февраля ...Применение свойства монотонности функций при решении уравнений и неравенств
Тамбовское областное государственное автономное образовательное учреждение – общеобразовательная школа – интернат. . «Мичуринский лицей». ...Применение формул сокращённого умножения
Кондратьева Марина Александровна. Учитель математики МБОУ «Северная средняя общеобразовательная школа». Первомайского района Алтайского края. ...Применение распределительного свойства умножения
Применение распределительного свойства умножения. . Форма урока. :. Урок – путешествие. . Тип урока. :. Урок обобщения и систематизации знаний. ...Применение свойств арифметического квадратного корня
ПЛАН-КОНСПЕКТ УРОКА «Применение свойств арифметического квадратного корня». . ФИО (полностью). . . Рыжова Наталья Михайловна. . ...Применение производной к построению графиков функций
Применение производной к построению графиков функций. Алгебра и начала анализа 11 класс. Автор: Димакова Ольга Николаевна – учитель математики ...Применение различных способов разложения на множители
Урок. Применение различных способов разложения на множители. Цели урока:. - закрепление навыков разложения на множители различными способами, ...Применение иррациональных уравнений при решении задач
Полуянова Н.Н. учитель математики. . СОШ № 21 г. Уральск. (алгебра и начала анализа 11 класс, профильный уровень). Конспект открытого ...Применение метода интервалов для решения неравенств
Применение метода интервалов для решения неравенств. . . 9-й класс. Цель урока:. рассмотреть применение метода интервалов для решения неравенств ...Применение графических и геометрических методов при решении текстовых задач
Тема урока. : Применение графических и геометрических методов при решении текстовых задач. (11 класс). Цели. :. Обучающая:. научить решать текстовые ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:8 сентября 2019
Категория:Математика
Содержит:24 слайд(ов)
Поделись с друзьями:
Скачать презентацию