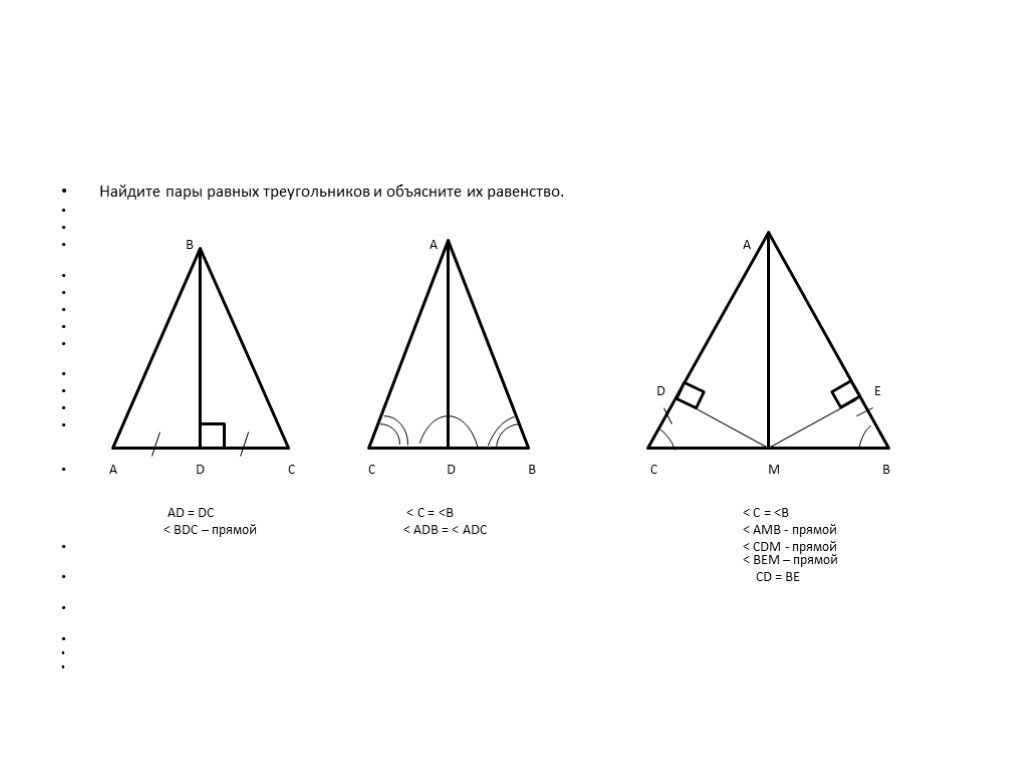
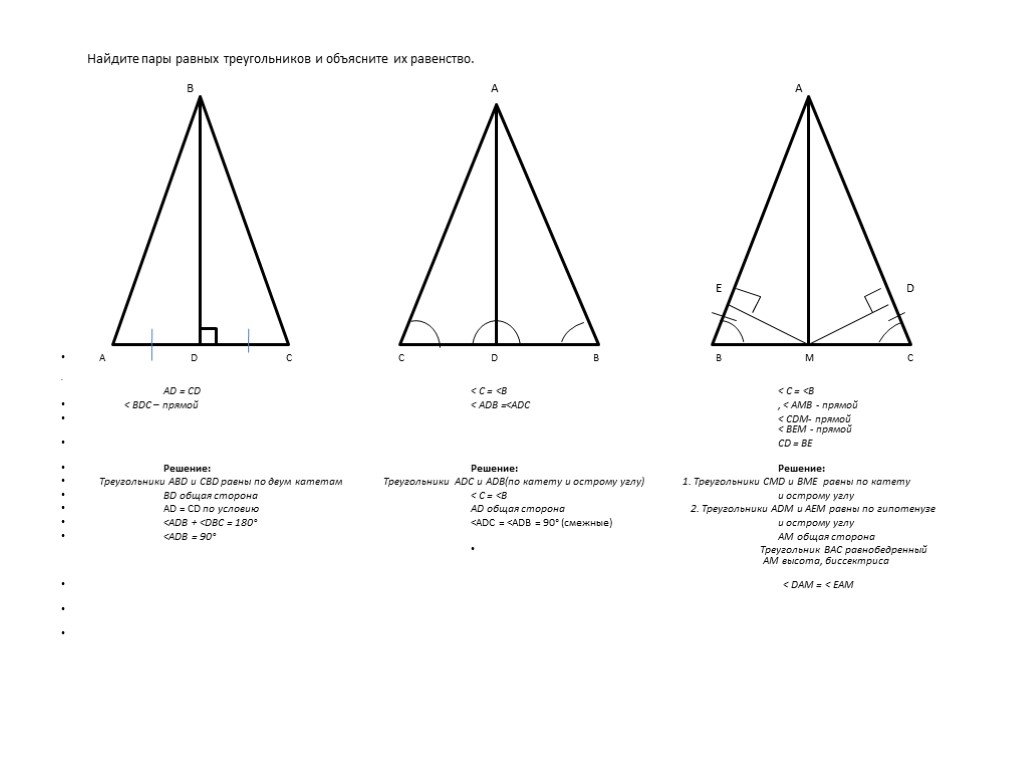
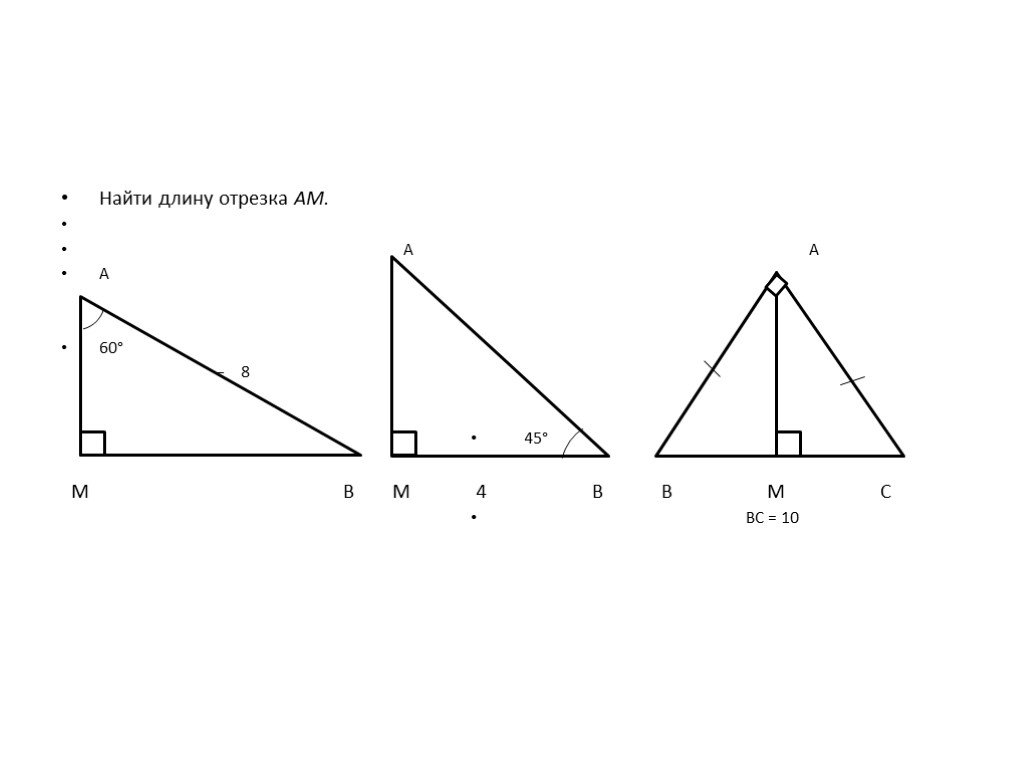
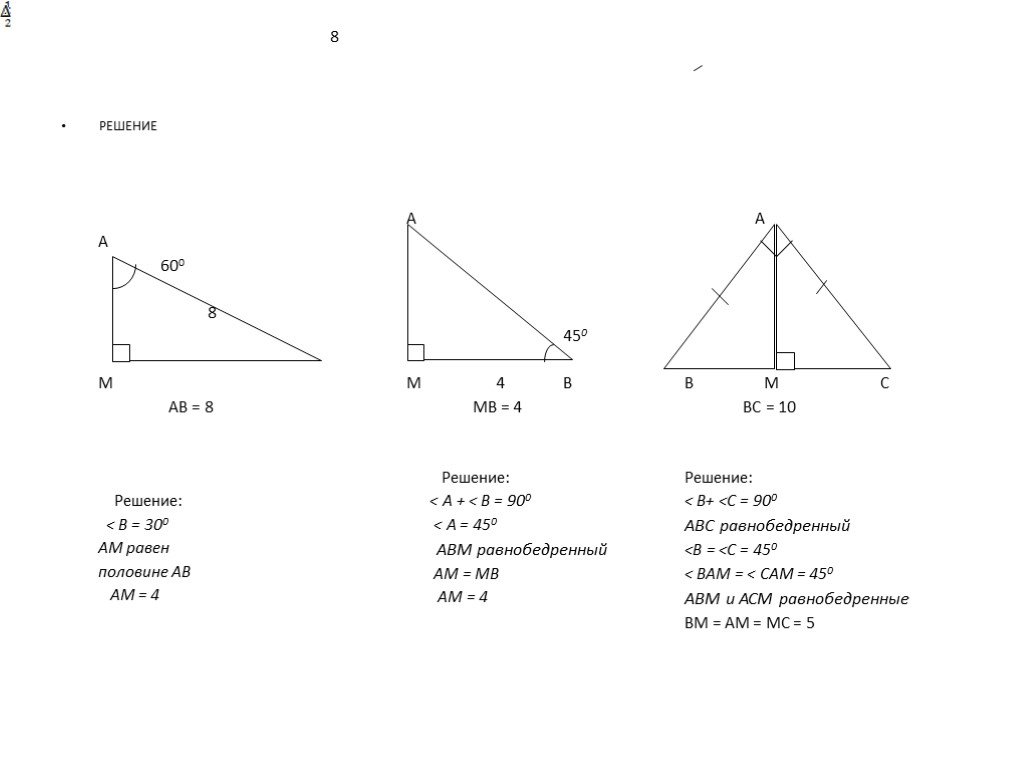
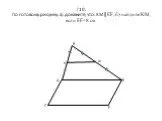
Презентация "Применение свойств и признаков равенства прямоугольных треугольников к решению практических задач" (7 класс) по математике – проект, доклад
Презентацию на тему "Применение свойств и признаков равенства прямоугольных треугольников к решению практических задач" (7 класс) можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 24 слайд(ов).
Слайды презентации
Список похожих презентаций
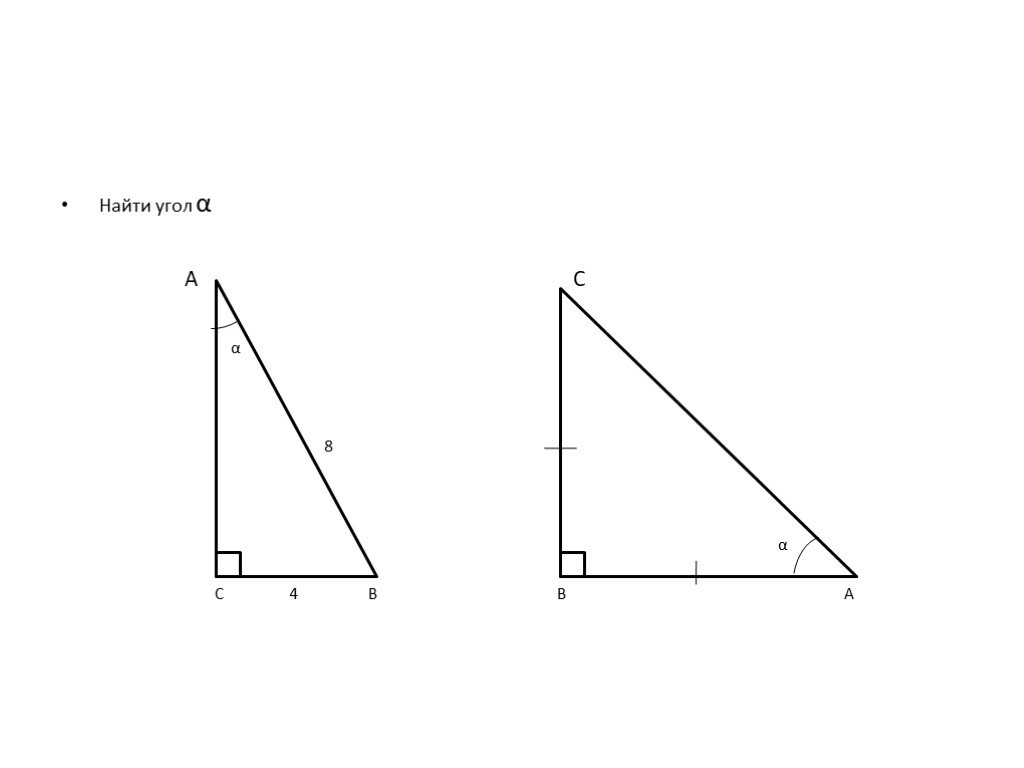
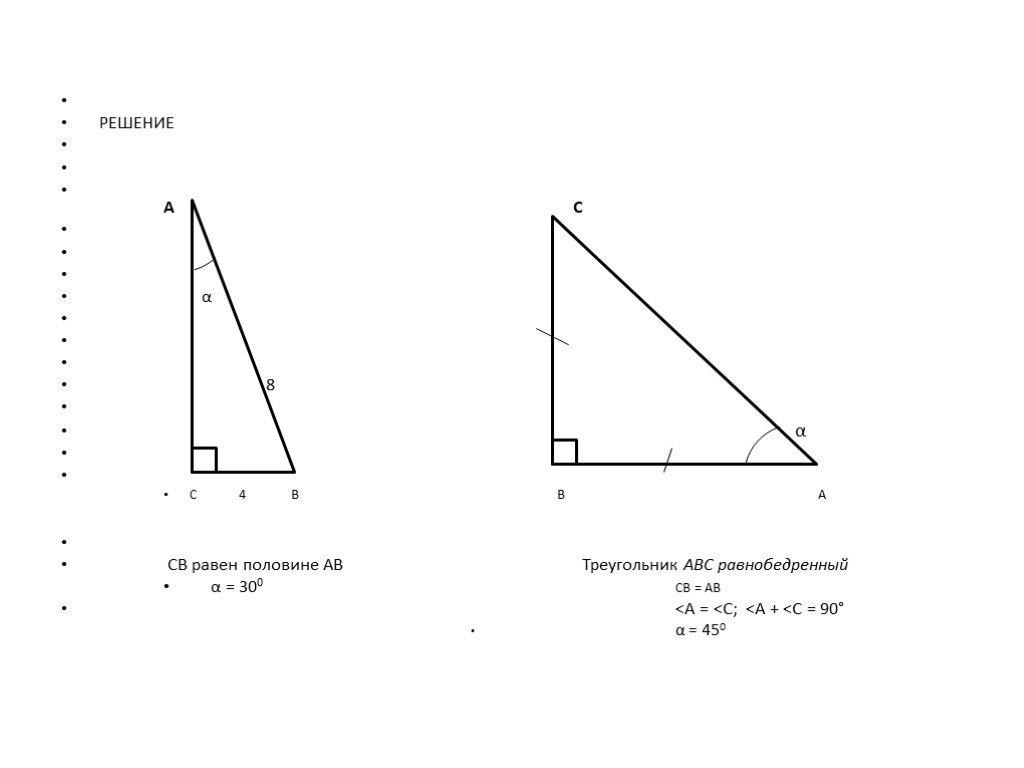
1 признак равенства треугольников
Цели урока:. ввести понятие теоремы и доказательства теоремы; доказать первый признак равенства треугольников; научиться решать задачи на первый признак ..."Треугольник. Первый признак равенства треугольников",
Работаем по плану:. Треугольник. определение; периметр; равные треугольники. Теорема. Первый признак равенства треугольников. Выбери треугольники. ...«Признаки равенства треугольников»
1.Цели и задачи занятия 2.Практическая работа 3.Таблица признаков равенства треугольников 4.Решение задач. Цели и задачи. 1. Усвоение материала через ...«Решение задач по математике»
10 февраля. В классе. Задача условие вопрос решение ответ. Быстро и правильно считать. Правильно записывать решение задачи. Кричать и сердиться, когда ..."Функция y = kx², ее свойства и график". 8-й класс
Траектория движения комет в межпланетном пространстве. Архитектурные сооружения. . Траектория движения. Тема урока. Функция у=кх2, ее график и свойства ...I Функция У=АХ², её график и свойства
А=1 У=Х ². А=2 У=2Х ². У=Х² У=2Х². Растяжение от оси Х в два раза. А=0.5 У=Х² У=0.5Х². Сжатие по оси Х в два раза. Вообще график функции У=АХ² можно ...Авторские задачи по математике и физике, составленные по повести Н.В. Гоголя «Ночь перед Рождеством
Методологическая основа: Класс арифметических задач огромен. Учащиеся старших классов обычно пытаются решать такие задачи алгебраически, так как владеют ..."Электрики и математика"
Воспитательные Воспитание умения работать в команде, уважения к сопернику, воспитание чувства ответственности; Воспитание чувства ответственности, ..."Целые числа и действия с ними". 6-й класс
«Сумма двух долгов есть долг». «Сумма имущества и долга равна их разности». (– 3) + (– 5) = – 8 4 + (– 7) = 4 – 7 = – 3. – 8 · (– 2) = 4; – 9 : (– ..."Турнир веселых и смекалистых знатоков истории, физики, химии, математики"
Цели мероприятия: 1.Развитие у учащихся интереса к изучаемым предметам. 2.Показать необходимость знаний по математике в других науках. 3.Формирование ..."Нахождение наибольшего и наименьшего значений непрерывной функции на промежутке
1. Найти наибольшее значение функции по её графику на [ -5;6] и [-7; 6]. 5 4 -5 у наиб. = 4 [-5; 6] у наиб. = 5 [-7; 6] 1. 2. Найти наименьшее значение ...«Параллельность прямых и плоскостей»
ABCD – трапеция, AD , E и F – середины AB и CD соответственно. Докажите, что EF ǁ α. α. α. α. α. A B C D α. Через вершины А и С параллелограмма ABCD ...Аксиомы расположения точек на прямой и плоскости
Выполните действия и сделайте записи:. 1. Изобразите точку С, лежащую на прямой а. 2. Изобразите точку D, не лежащую на этой прямой. 3. Проведите ...Cинус, косинус, тангенс и котангенс угла
Тест. Синус угла А равен: а) 4/5; б) 3/5; в) 4/3 2.Тангенс угла В равен: а) 4/3; б) 3/5; в)¾ 3.Косинус. равен : а) б) ½; в). 4. Упростить выражение:. ..."Комбинаторика и вероятность"
Диктант ******- это раздел математики, посвященный задачам выбора и расположения предметов из различных множеств. Произведение натуральных чисел от ...«Треугольники и их виды»
Геометрические фигуры. а ж е д с б и з. Треугольники и их виды. Определение треугольника, элементы треугольника Виды треугольников Сумма углов треугольника ...«Закрепление изученого» (Сложение и вычитание с переходом через десяток в пределах 20)
Цели урока:. 1. Закрепить знания о сложении и вычитании с переходом через десяток в приделах 20. 2. Упражняться в решении задач изученных видов. План ...«Решение задач с помощью пропорций»
Найти значение Х: Х:3=4:6 5:Х=2:6 7:3=Х:18 Устная работа. Указать вид пропорциональной зависимости:. Какова зависимость пути от времени? Какова зависимость ...«Решение задания С1 ЕГЭ по информатике и ИКТ»
2 балла. Решение задания С1 ЕГЭ по информатике и ИКТ. Кунина В.В. область I область II. 0 x y y = x+2 y2 + x2 = 25 y2 + x2 25 y 0 x 0 область ...«Математический бой. Через тернии к звездам»
. Разминка. Сколько разных букв в названии нашей страны? 5 букв. ДВЕНАДЦАТЬ. К семи прибавить пять. Как правильно записать: одиннадцать или адиннадцать? ...Конспекты
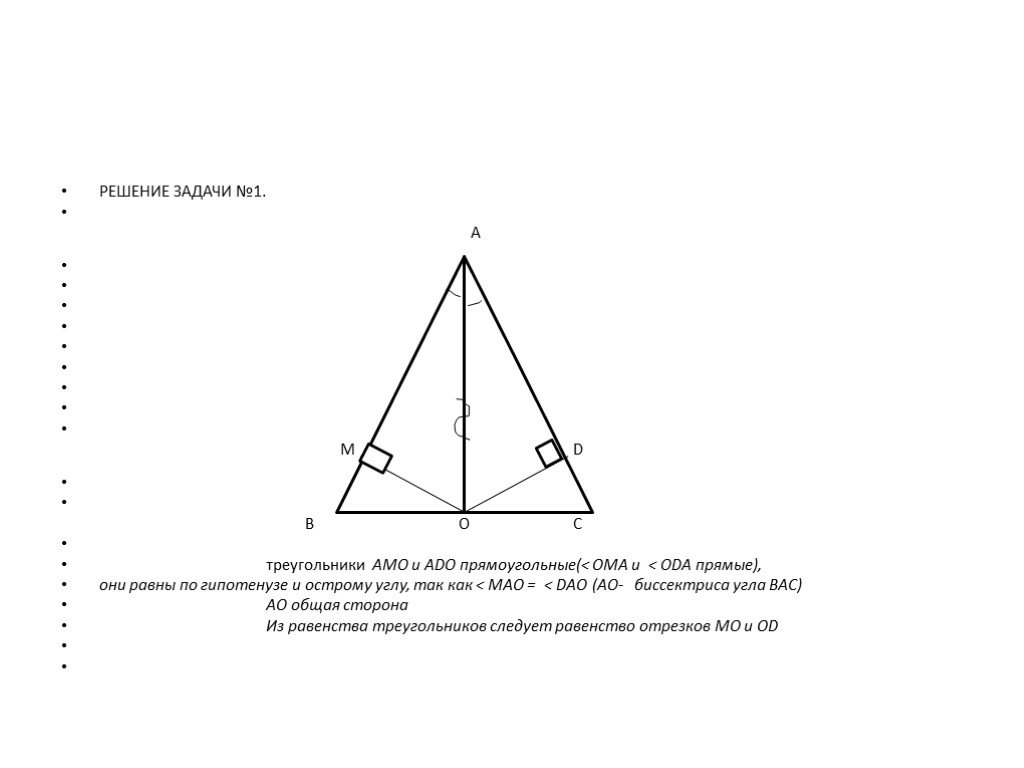
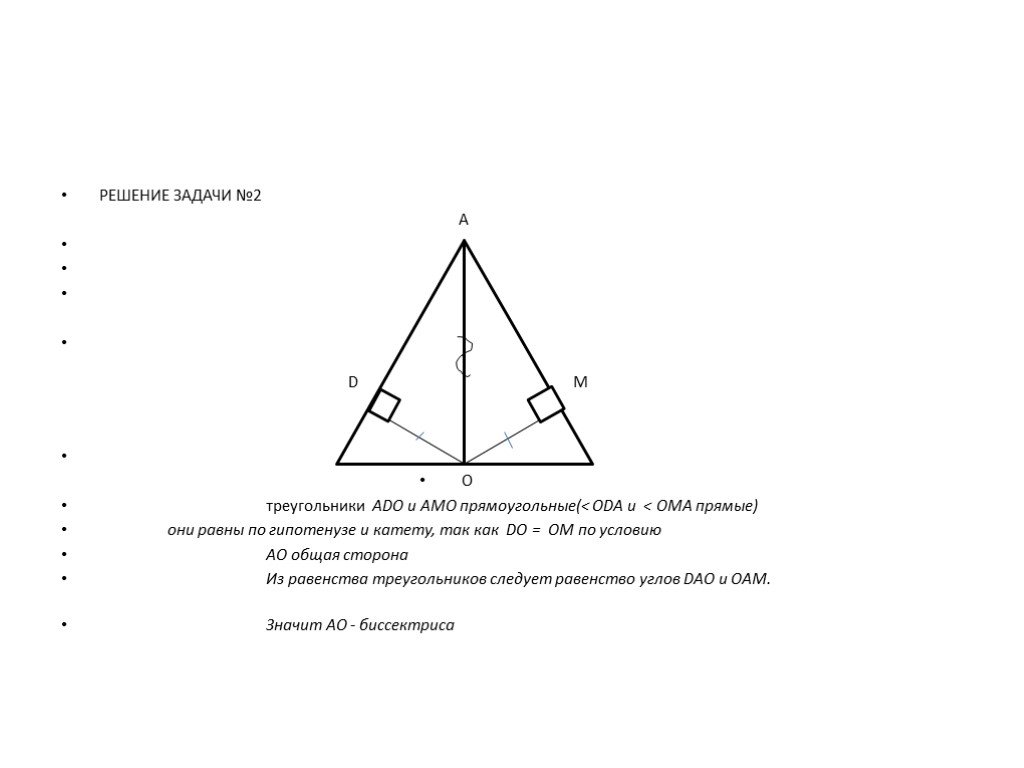
I признак равенства треугольников в задачах
ТЕМА УРОКА:. I. признак равенства треугольников в задачах. ТИП УРОКА. : закрепление изученного материала. КОНТИНГЕНТ УЧАЩИХСЯ:. 7 класс. ...Арифметический квадратный корень и его свойства
Конспект урока математики в 10 классе. Жирнова С.В. учитель математики. Тема урока:. «Арифметический квадратный корень и его свойства». Тип урока. ...Арифметический квадратный корень и его свойства
Тема: «Арифметический квадратный корень и его свойства». Урок-игра «Аукцион математических знаний». Цели урока. :. . Образовательные:. - ...Арифметический корень натуральной степени и его свойства
Урок алгебры в 9 классе. . Тема урока. : «Арифметический корень натуральной степени и его свойства». . Из опыта работы учителя математики. ...Буквенная запись свойств сложения и вычитания
Муниципальное автономное общеобразовательное учреждение. Чурилковская средняя общеобразовательная школа. Домодедовского района Московской области. ...Web -разработка. Применение производной.10 класс
ТЕХНОЛОГИЧЕСКАЯ КАРТА КОНСТРУИРОВАНИЯ УРОКА С ИСПОЛЬЗОВАНИЕ СРЕДСТВ ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ. Учитель Беломестнова Наталья Петровна. Предмет, ...Арифметический квадратный корень и его свойства
Урок - повторение по теме: «Арифметический квадратный корень и его свойства». . . Учитель Переверзева М.В. МБОУСОШ «11. . Цель: подвести итоги ...Арифметическая и геометрическая прогрессии
Тема урока:. «Арифметическая и геометрическая прогрессии». . Цель урока:. Систематизировать и обобщить знания учащихся по теме «Арифметическая и ...Арифметическая и геометрическая прогрессии
Тема: Арифметическая и геометрическая прогрессии. Тип урока:. урок обобщения и систематизации знаний. Цель:. актуализация имеющиеся знания ...Арифметическая и геометрическая прогрессии
ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧЕРЕЖДЕНИЕ. . СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА №1918. . Конспект урока по алгебре ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:7 мая 2018
Категория:Математика
Классы:
Содержит:24 слайд(ов)
Поделись с друзьями:
Скачать презентацию