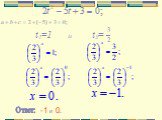Презентация "Показательные уравнения" (11 класс) по математике – проект, доклад
Презентацию на тему "Показательные уравнения" (11 класс) можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 28 слайд(ов).
Слайды презентации
Список похожих презентаций
Показательные уравнения
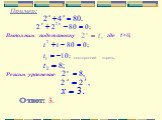
Показательные уравнения – это уравнения, содержащие переменную в показателе степени. Решение показательных уравнений часто сводится к решению уравнения ...Показательные уравнения
Показательные. Цели урока: 1. ввести понятие показательных уравнений; 2. формировать умение решать показательные уравнения основными методами: функционально-графическим, ...Показательные уравнения
“Метод решения хорош, если с самого начала мы можем предвидеть – и далее подтвердить, что следуя этому методу, мы достигнем цели”. (Г.Лейбниц). Решите ...Показательные уравнения
. Основные задачи: 1.Повышение профессиональной квалификации учителей в области применения ИКТ в сочетании с другими педагогическими технологиями. ...Показательные уравнения и неравенства
"Что значит решить задачу? Это значит свести ее к уже решенным". С.А. Яновская. - Какие из данных уравнений являются показательными? 12). Определение. ...Показательные уравнения
Математический диктант. Запишите функции. 1. Постройте схематично графики. 2. Выпишите убывающие функции 3. Для каждой из функций запишите множество ...Показательные уравнения и неравенства
Цель урока: обобщение знаний о способах решения показательных уравнений и неравенств, подготовка к ЕГЭ. 2. 1. если , то если , то решений нет. Показательные ...Показательные уравнения и способы их решения
Определение: Показательные уравнения – уравнения, в которых переменная входит только в показатели степеней при постоянных основаниях. Например,. Основные ...Показательные уравнения, методы их решения
Что же такое показательные уравнения ? Показательные уравнения – это уравнения, в которых неизвестное число находится в показателе степени. Чаще всего ...Показательная функция. Показательные уравнения
Автор: Кашина Галина Васильевна, преподаватель математики Тип урока: урок обобщения, систематизации знаний. Цели урока: Образовательные: Обобщить ...Показательные уравнения. Подготовка к ЕГЭ
Обобщающий урок по теме «Показательные уравнения» Подготовка к ЕГЭ. Всякое умение трудом даётся Цель: Повторить и обобщить материал по теме «Показательные ...Простейшие показательные уравнения
Цели урока.Выявить общий вид показательного уравнения Выяснить способы его решения Научиться решать простейшие показательные уравнения. Решите уравнения ...
Диофантовы уравнения
Цели и задачи. Определение диофантова уравнения Биография Диофанта Диофантовые уравнения первой степени Диофантовые уравнения высших степеней Проект ...Неполные квадратные уравнения
Математику нельзя изучать, наблюдая, как это делает сосед! А. Нивен. 1. Какое уравнение называется квадратным? 2. Может ли коэффициент а в квадратном ...Определение квадратного уравнения. Неполные квадратные уравнения
Решите уравнения Х=±2 Х=± Корней нет Х=0 Х=0,Х=2. 5х-2=0. Разделите данные уравнения на две группы. Какие уравнения называются квадратными? 1. Уравнение ...Урок математики по ФГОС "Уравнение.Корень уравнения"
Китайская мудрость. Расскажи мне, и я забуду. Покажи мне, и я запомню. Дай мне попробовать, и я научусь. Актуализация знаний. 90 45 84 72 8 - 45 : ...Целые уравнения
Стоя на одном месте, новых горизонтов не откроешь. УСТНАЯ РАБОТА. Решите уравнение: ♦ Сколько корней имеет линейное и квадратное уравнение? х=-2 корней ...Дифференциальные уравнения высших порядков
1. Общие сведения. Определение. Дифференциальное уравнение содержащее производную функции двух и более порядков, называется дифференциальным уравнением ...Тригонометрические уравнения
I. Повторение и актуализация. 1. Что значит простейшая тригонометрическая функция? 2. Приведите пример простейшего тригонометрического уравнения. ...Иррациональные уравнения
Домашнее задание:. Обязательное задание. Сложное задание. Задание повышенной сложности. «ХОД КОНЕМ» НИИ И НАЛЬ ШЕ ЕЮ ЗО У РЕА ИР ПОСТА НИЙ РЕ ДИ ЦИО ...Конспекты
Показательные уравнения
Тема урока: «Показательные уравнения», 11 класс. Цели:. Образовательные: актуализация опорных знаний при решение показательных уравнений, обобщение ...Показательные уравнения
Филиал боу СПО. «. ЧЕБОКСАРСКИЙ МЕДИЦИНСКИЙ КОЛЛЕДЖ. ». минздравсоцразвития чувашии Г. КАНАШ чувашской республики. . «. Утверждаю. ». . зав ...Показательные уравнения
ТЕМА «Показательные уравнения». Цели:. 1.Познакомиться с разными видами показательных уравнений, научиться различать разные виды показательных уравнений, ...Показательные уравнения и их системы
Тема: «Показательные уравнения и их системы». Цели:. Образовательная:. рассмотреть способы решения показательных неравенств и способствовать выработке ...Показательные уравнения и неравенства
. КГУ "Средняя школа №11 отдела образования акимата г. Тараз". Открытый урок. «Показательные уравнения и неравенства». . Класс. : ...Показательные уравнения и неравенства
Технологическая карта урока по математике в 10 классе. по теме: «Показательные уравнения и неравенства». Учитель Бондарь Ирина Рувиновна. Предмет. ...Показательные уравнения
Учитель. : Моисеева Е.В. . . Предмет:. алгебра. Класс - 10. Тема урока. . Показательные уравнения. Единица содержания. . Основной способ ...Показательные функции, уравнения, неравенства
Обобщающий урок. по теме:. Учитель математики филиала. . БОУ ХМАО - Югры В(с)ОШ. при ИР 99/15 г.Нижневатовска. ...Свойства логарифмов. Логарифмические и показательные уравнения и неравенства
Муниципальное бюджетное образовательное учреждение. . «Средняя общеобразовательная школа № 7» им. О.Н. Мамченкова. . г. Елизово, Камчатский край. ...Повторение: логарифмы, логарифмические уравнения
Преподаватель: Гаученова Валентина Петровна. Забайкальский край. Государственное профессиональное образовательное учреждение «Чернышевское многопрофильное ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:26 июня 2016
Категория:Математика
Классы:
Содержит:28 слайд(ов)
Поделись с друзьями:
Скачать презентацию