Презентация "ГИА-2013г. Модуль АЛГЕБРА №6" – проект, доклад
Презентацию на тему "ГИА-2013г. Модуль АЛГЕБРА №6" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 18 слайд(ов).
Слайды презентации
Список похожих презентаций
ГИА 2013. Модуль алгебра №6
ГИА – 2013 г. Модуль «Алгебра» №6. «ГИА-2013. Математика: типовые экзаменационные варианты: 30 вариантов» под редакцией А. Л. Семенова, И. В. Ященко. ...ГИА 2013. Модуль АЛГЕБРА №7
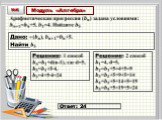
Модуль «Алгебра» №4. 1 способ: (a+b)²(a-b)²=(a²+2ab+b²)(a²-2ab+b²)= =a⁴-2a³b+a²b²+2a³b-4a²b²+2ab³+a²b²-2ab³+b⁴= = a⁴-2a²b²+b⁴. Повторение (5) Ответ: ...ГИА 2013. Модуль алгебра №8
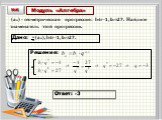
Модуль «Алгебра» №8. Повторение (4). Решите неравенство 7+2(х-4)≥х+4. Ответ: [-3;+∞). Повторение (подсказка). При решении неравенства можно переносить ...ГИА 2013. Модуль алгебра №3
Модуль «Алгебра» №3. Наибольшее число :. Повторение (4). Укажите наибольшее из чисел:. Ответ: ⎕ ⎕ ⎕ ⎕. Повторение (подсказка). Чтобы сравнить выражения, ...ГИА 2013. Модуль «Алгебра» №1
Модуль «Алгебра» №1. Повторение (1). Найдите значение выражения 0,5 ∙ 0,05 ∙ 0,005 . Ответ: 0,000125 0,5 ∙ 0,05 ∙ 0,005 = 1 + 3 6 000 =0,. Повторение ...ГИА 2013. Модуль алгебра №1
Модуль «Алгебра» №1. Повторение (1). Найдите значение выражения 0,5 ∙ 0,05 ∙ 0,005 . Ответ: 0,000125 0,5 ∙ 0,05 ∙ 0,005 = 1 + 3 6 000 =0,. Повторение ...ГИА 2013. Модуль алгебра №2
Модуль «Алгебра» №2. Повторение (2). На координатной прямой отмечено число а. Из следующих неравенств выберите верное:. Ответ: 3. Исходя из рисунка ...ГИА 2013. Модуль АЛГЕБРА (№8)
Модуль «Алгебра» №8. Повторение (4). Решите неравенство 7+2(х-4)≥х+4. Ответ: [-3;+∞). Повторение (подсказка). При решении неравенства можно переносить ...ГИА 2013. Модуль АЛГЕБРА (№4)
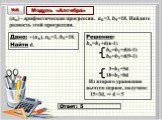
Модуль «Алгебра» №4. Повторение (3) Ответ: -6 Решите уравнение. Повторение (подсказка). В уравнении можно делить обе части уравнения на одно и то ...ГИА 2013. Модуль «Алгебра» №7
Модуль «Алгебра» №3. Наибольшее число :. Повторение (4). Укажите наибольшее из чисел:. Ответ: ⎕ ⎕ ⎕ ⎕. Повторение (подсказка). Чтобы сравнить выражения, ...Разбор первой части ГИА по математике. Модуль Геометрия
Теоретическая часть.12 задание. Что такое cos, sin, tg и ctg ?Нам сейчас достаточно знать, что отношения сторон в треугольнике. sin. Теорема Пифагора. ...Модуль числа
0 1 F N R L A. Какие из данных точек имеют противоположные координаты? Назовите координаты точек, отмеченных на координатной прямой. Какие числа называются ...Модуль числа
...Модуль числа
Цели и задачи. Научить учащихся использовать понятие модуля числа на практике при решении задач Показать различные приемы решения Активизировать самостоятельную ...ГИА Модуль РЕАЛЬНАЯ МАТЕМАТИКА №17
Модуль «РЕАЛЬНАЯ МАТЕМАТИКА» №17. Повторение (2) Ответ: 480. Найти расстояние от проектора С до экрана В. А В 180 см 90 см 240 см С H₁ H. Луч проектора ...ГИА 2013. Модуль Геометрия №13
Повторение(3) Ответ: 23. Укажите номера верных утверждений. 1.Через любые три различные точки плоскости можно провести единственную прямую. 2.Если ...ГИА – 2013 г. Модуль «Реальная математика». №14
ГИА – 2013 г. Модуль «Реальная математика». №14. «ГИА-2013. Математика: типовые экзаменационные варианты: 30 вариантов» под редакцией А. Л. Семенова, ...ГИА 2013 Модуль «Геометрия» № 11
Модуль «ГЕОМЕТРИЯ» №11. Повторение (3) Ответ: 6. Найти площадь треугольника. В С А 8 3 30⁰. Повторение. Площадь треугольника равна половине произведения ...ГИА 2013. Модуль Геометрия №12
Модуль «ГЕОМЕТРИЯ» №12. Повторение (3) Ответ: 45. Найти угол АВС (в градусах). В С А. Проведем из произвольной точки луча ВА перпендикуляр до пересечения ...Модуль
Пояснительная записка. Данный элективный курс направлен на расширение знаний учащихся, повышение уровня математической подготовки через решение большого ...Конспекты
Модуль числа. Сравнение чисел
Конспект урока для 6 класса «Модуль числа. Сравнение чисел». ТЕМА УРОКА:. Цели урока:. . Обучающая:. повторить определение модуля и правила ...Противоположные числа. Модуль числа
Конспект урока по математике в 6 классе. . разработала учитель математики УВК «Уютненская школа-гимназия». . Костюкова Ольга Владимировна. , Республика ...Модуль числа
Муниципальное общеобразовательное учреждение. «Средняя общеобразовательная школа №1 г.Суздаля». Учитель математики: Плотникова Т.В. . Конспект ...Модуль числа
. План-конспект урока математики в 6 классе. по теме «Модуль числа». Цели урока:. Повторить основные понятия по теме «Координаты на прямой. ...Модуль числа
Урок-игра по теме: Модуль числа. Форма проведения: комбинированный урок. Цели:. Образовательные:. организовать деятельность учащихся на отработку ...Модуль числа
УРОК. 6 класс по теме:. Тема урока. : Модуль числа. Цель урока. : - ввести понятие модуля числа;. ...Модуль рационального числа
Котвицкая Ирина Юрьевна. Любимовская НСШ. учитель математики. Урок математики по теме «Модуль рационального числа». . Тип урока. : урок ...Модуль действительного числа
Тема:. Модуль действительного числа. Цель урока:. . Коммуникативная:. уметь выслушивать мнение одноклассников и анализировать, делать выводы обоснованно ...Модуль действительного числа
. Выполнила. . Степанова Валентина Яковлевн. -учитель математики ГБОУ СОШ №1 «ОЦ». . Ж.-д.ст. Шентала Самарской области. г. . . Конспект ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:15 января 2015
Категория:Математика
Содержит:18 слайд(ов)
Поделись с друзьями:
Скачать презентацию