Презентация "ГИА 2013. Модуль алгебра №8" – проект, доклад
Презентацию на тему "ГИА 2013. Модуль алгебра №8" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 20 слайд(ов).
Слайды презентации
Список похожих презентаций
ГИА 2013. Модуль АЛГЕБРА (№8)
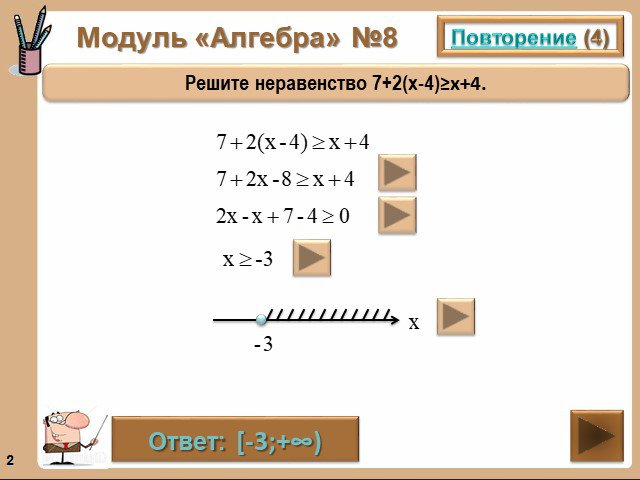
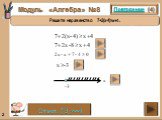
Модуль «Алгебра» №8. Повторение (4). Решите неравенство 7+2(х-4)≥х+4. Ответ: [-3;+∞). Повторение (подсказка). При решении неравенства можно переносить ...ГИА-2013г. Модуль АЛГЕБРА №6
ГИА – 2013 г. Модуль «Алгебра» №6. «ГИА-2013. Математика: типовые экзаменационные варианты: 30 вариантов» под редакцией А. Л. Семенова, И. В. Ященко. ...ГИА 2013. Модуль «Алгебра» №1
Модуль «Алгебра» №1. Повторение (1). Найдите значение выражения 0,5 ∙ 0,05 ∙ 0,005 . Ответ: 0,000125 0,5 ∙ 0,05 ∙ 0,005 = 1 + 3 6 000 =0,. Повторение ...ГИА 2013. Модуль «Алгебра» №7
Модуль «Алгебра» №3. Наибольшее число :. Повторение (4). Укажите наибольшее из чисел:. Ответ: ⎕ ⎕ ⎕ ⎕. Повторение (подсказка). Чтобы сравнить выражения, ...ГИА 2013. Модуль АЛГЕБРА №7
Модуль «Алгебра» №4. 1 способ: (a+b)²(a-b)²=(a²+2ab+b²)(a²-2ab+b²)= =a⁴-2a³b+a²b²+2a³b-4a²b²+2ab³+a²b²-2ab³+b⁴= = a⁴-2a²b²+b⁴. Повторение (5) Ответ: ...ГИА 2013. Модуль алгебра №3
Модуль «Алгебра» №3. Наибольшее число :. Повторение (4). Укажите наибольшее из чисел:. Ответ: ⎕ ⎕ ⎕ ⎕. Повторение (подсказка). Чтобы сравнить выражения, ...ГИА 2013. Модуль алгебра №6
ГИА – 2013 г. Модуль «Алгебра» №6. «ГИА-2013. Математика: типовые экзаменационные варианты: 30 вариантов» под редакцией А. Л. Семенова, И. В. Ященко. ...ГИА 2013. Модуль алгебра №1
Модуль «Алгебра» №1. Повторение (1). Найдите значение выражения 0,5 ∙ 0,05 ∙ 0,005 . Ответ: 0,000125 0,5 ∙ 0,05 ∙ 0,005 = 1 + 3 6 000 =0,. Повторение ...ГИА 2013. Модуль алгебра №2
Модуль «Алгебра» №2. Повторение (2). На координатной прямой отмечено число а. Из следующих неравенств выберите верное:. Ответ: 3. Исходя из рисунка ...ГИА 2013. Модуль АЛГЕБРА (№4)
Модуль «Алгебра» №4. Повторение (3) Ответ: -6 Решите уравнение. Повторение (подсказка). В уравнении можно делить обе части уравнения на одно и то ...ГИА 2013. Модуль алегбра №4
Модуль «Алгебра» №4. Повторение (3) Ответ: -6 Решите уравнение. Повторение (подсказка). В уравнении можно делить обе части уравнения на одно и то ...ГИА 2013. Модуль Геометрия №13
Повторение(3) Ответ: 23. Укажите номера верных утверждений. 1.Через любые три различные точки плоскости можно провести единственную прямую. 2.Если ...ГИА 2013. Модуль ГЕОМЕТРИЯ (№10)
Модуль «ГЕОМЕТРИЯ» №10. Повторение (2) Ответ: 4. Найти АС. В С А 5 ⇒. По теореме Пифагора. Повторение. Косинус острого угла прямоугольного треугольника ...ГИА 2013. Модуль Геометрия №10
Модуль «ГЕОМЕТРИЯ» №10. Повторение (2) Ответ: 4. Найти АС. В С А 5 ⇒. По теореме Пифагора. Повторение. Косинус острого угла прямоугольного треугольника ...ГИА 2013 Модуль «Геометрия» № 9
Модуль «ГЕОМЕТРИЯ» №9. Ответ: 70 Повторение (2). Повторение. В равнобедренном треугольнике углы при основании равны. В треугольнике сумма углов ...ГИА 2013 Модуль «Геометрия» № 11
Модуль «ГЕОМЕТРИЯ» №11. Повторение (3) Ответ: 6. Найти площадь треугольника. В С А 8 3 30⁰. Повторение. Площадь треугольника равна половине произведения ...ГИА 2013. Модуль Геометрия №11
Модуль «ГЕОМЕТРИЯ» №11. Повторение (3) Ответ: 6. Найти площадь треугольника. В С А 8 3 30⁰. Повторение. Площадь треугольника равна половине произведения ...ГИА – 2013 г. Модуль «Реальная математика». №14
ГИА – 2013 г. Модуль «Реальная математика». №14. «ГИА-2013. Математика: типовые экзаменационные варианты: 30 вариантов» под редакцией А. Л. Семенова, ...ГИА 2013. Модуль Геометрия №12
Модуль «ГЕОМЕТРИЯ» №12. Повторение (3) Ответ: 45. Найти угол АВС (в градусах). В С А. Проведем из произвольной точки луча ВА перпендикуляр до пересечения ...ГИА 2013. Модуль ГЕОМЕТРИЯ (№13)
Повторение(3) Ответ: 23. Укажите номера верных утверждений. 1.Через любые три различные точки плоскости можно провести единственную прямую. 2.Если ...Конспекты
Элементы теории вероятности в ГИА
13 апреля 2011г. Урок алгебры в 9 классе по теме:. . «Элементы теории вероятности в ГИА». Цели:. - Научиться анализировать и решать задачи ...Решение планиметрических задач при подготовке к ГИА
Открытый урок по геометрии в 9а классе. «Решение планиметрических задач при подготовке к ГИА». Учитель: Токмакова И.В. (высшая квалификационная ...Функции и их графики. Подготовка к ГИА
. Государственное бюджетное общеобразовательное учреждение. средняя общеобразовательная школа №625. с углублённым изучением математики Невского ...Подготовка к ГИА в новой форме
Шкредова Г. М.,. . учитель высшей категории. МОУ «Новоигирменская СОШ №3». Нижнеилимского района. . Иркутской области. . Урок-консультация ...Противоположные числа. Модуль числа
Конспект урока по математике в 6 классе. . разработала учитель математики УВК «Уютненская школа-гимназия». . Костюкова Ольга Владимировна. , Республика ...Модуль числа
. План-конспект урока математики в 6 классе. по теме «Модуль числа». Цели урока:. Повторить основные понятия по теме «Координаты на прямой. ...Модуль числа. Сравнение чисел
Конспект урока для 6 класса «Модуль числа. Сравнение чисел». ТЕМА УРОКА:. Цели урока:. . Обучающая:. повторить определение модуля и правила ...Модуль числа
Урок-игра по теме: Модуль числа. Форма проведения: комбинированный урок. Цели:. Образовательные:. организовать деятельность учащихся на отработку ...Модуль числа
Муниципальное общеобразовательное учреждение. «Средняя общеобразовательная школа №1 г.Суздаля». Учитель математики: Плотникова Т.В. . Конспект ...Модуль числа
УРОК. 6 класс по теме:. Тема урока. : Модуль числа. Цель урока. : - ввести понятие модуля числа;. ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:14 сентября 2014
Категория:Математика
Автор презентации:Учитель математики, Гладунец Ирина Владимировна
Содержит:20 слайд(ов)
Поделись с друзьями:
Скачать презентацию























![Решите неравенство -2х²-5х≥-3. Ответ: [-0,5; -3]. Рассмотрим соответствующую функцию у = -2х²-5х+3. Её график – парабола, ветви направлены вниз (а Решите неравенство -2х²-5х≥-3. Ответ: [-0,5; -3]. Рассмотрим соответствующую функцию у = -2х²-5х+3. Её график – парабола, ветви направлены вниз (а](https://prezentacii.org/upload/cloud/14/09/6121/images/thumbs/screen10.jpg)





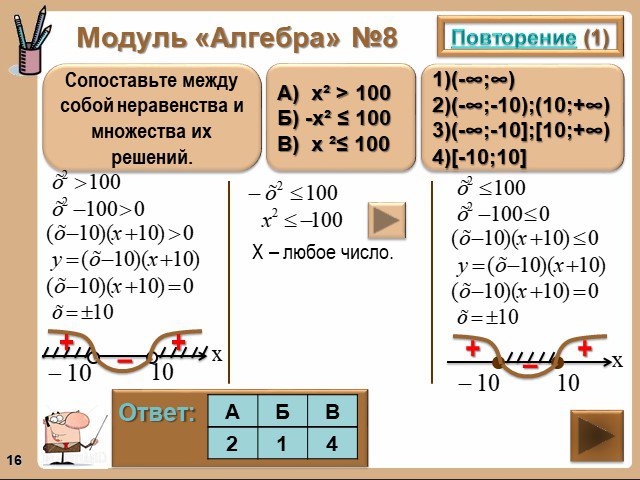
![Повторение (1). Сопоставьте между собой неравенства и множества их решений. Ответ: 1)(-∞;∞) 2)(-∞;-10);(10;+∞) 3)(-∞;-10];[10;+∞) 4)[-10;10]. А) х² > 100 Б) -х² ≤ 100 В) х ²≤ 100. Х – любое число. Повторение (1). Сопоставьте между собой неравенства и множества их решений. Ответ: 1)(-∞;∞) 2)(-∞;-10);(10;+∞) 3)(-∞;-10];[10;+∞) 4)[-10;10]. А) х² > 100 Б) -х² ≤ 100 В) х ²≤ 100. Х – любое число.](https://prezentacii.org/upload/cloud/14/09/6121/images/thumbs/screen16.jpg)


































