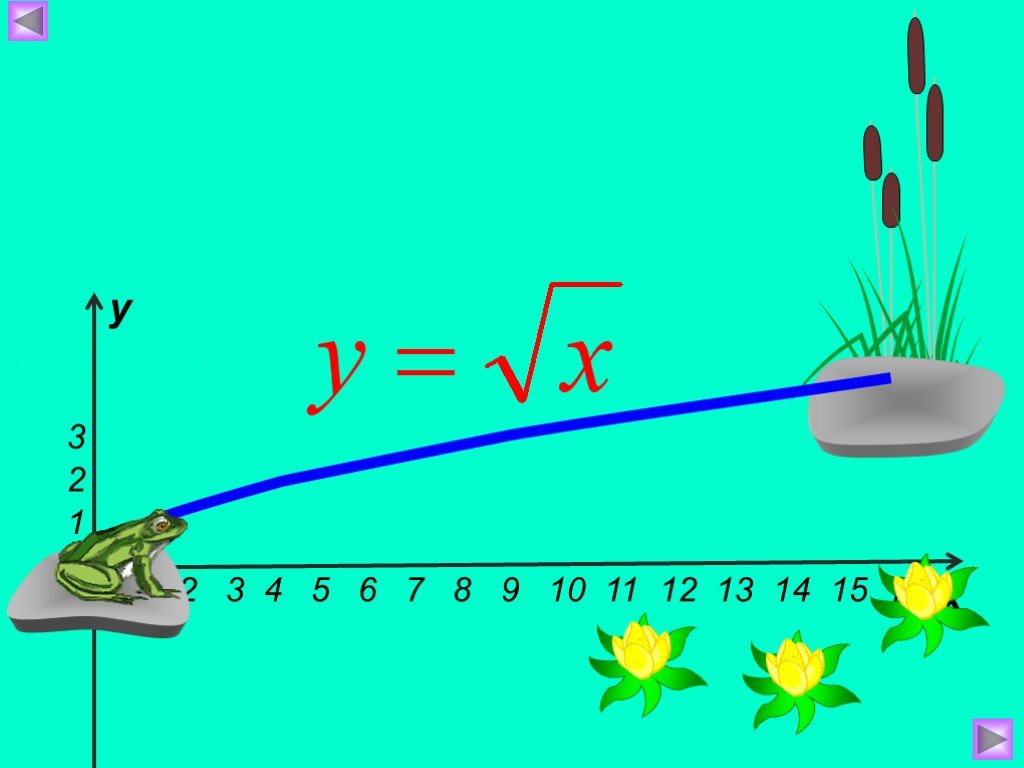
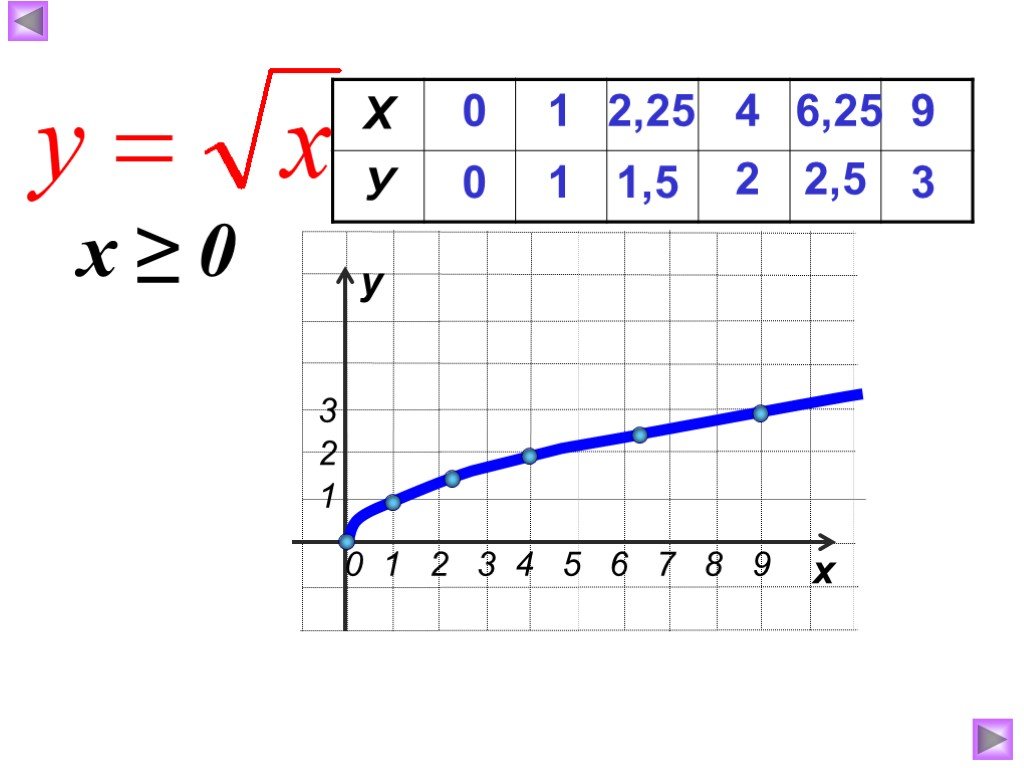
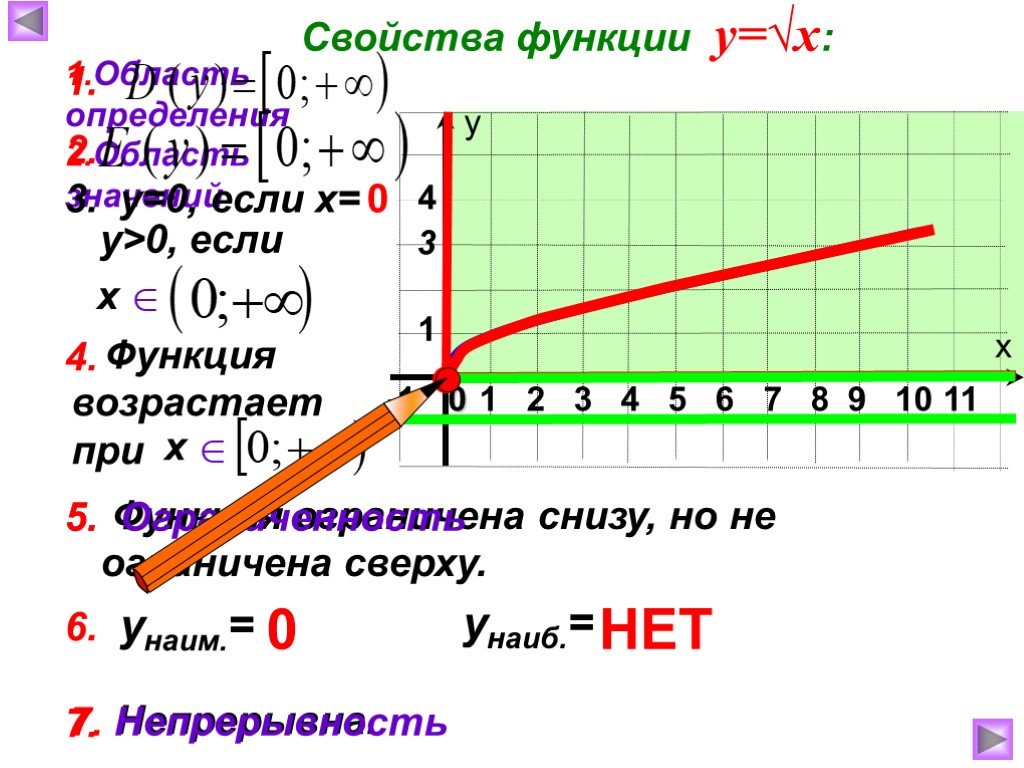
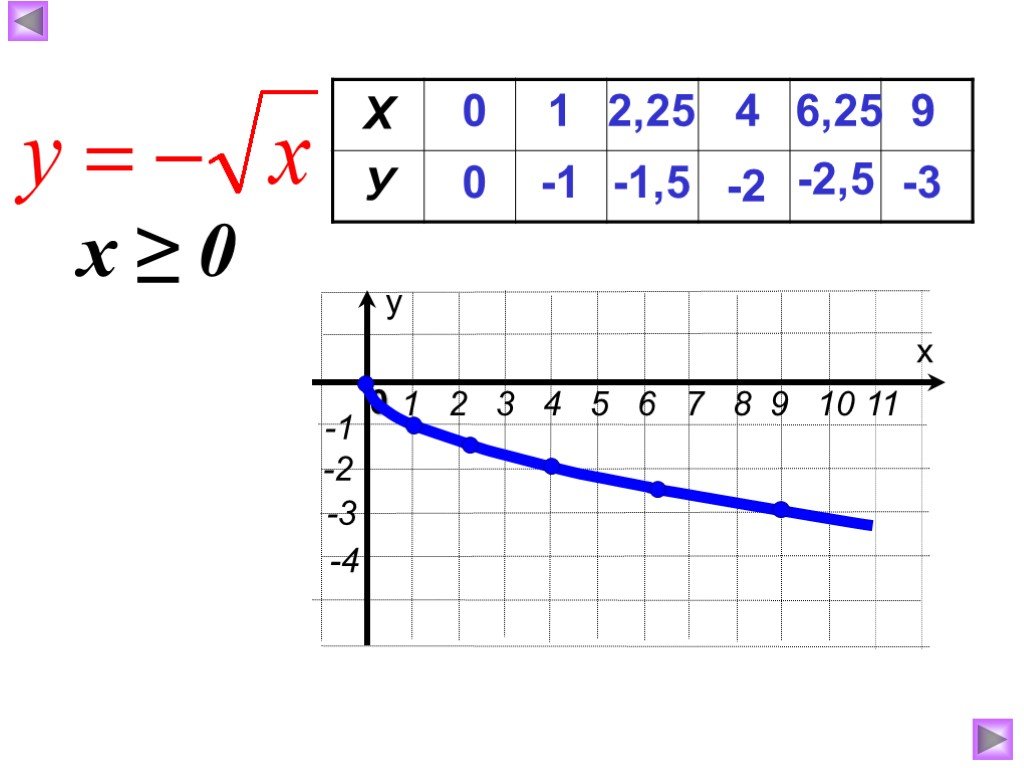
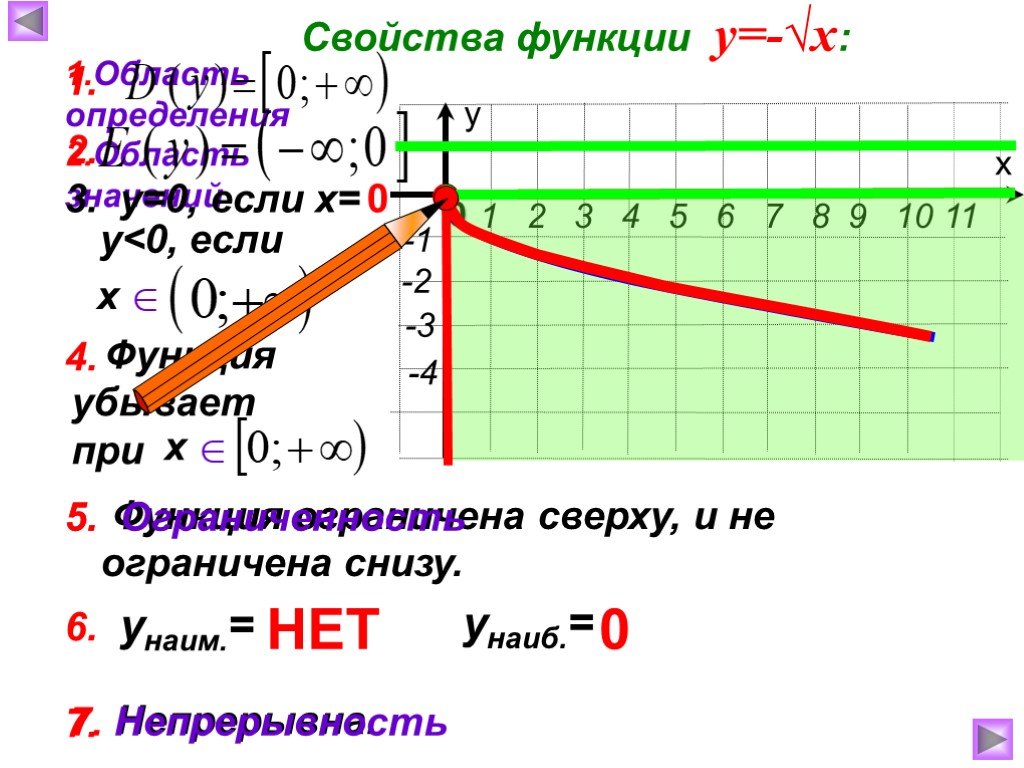
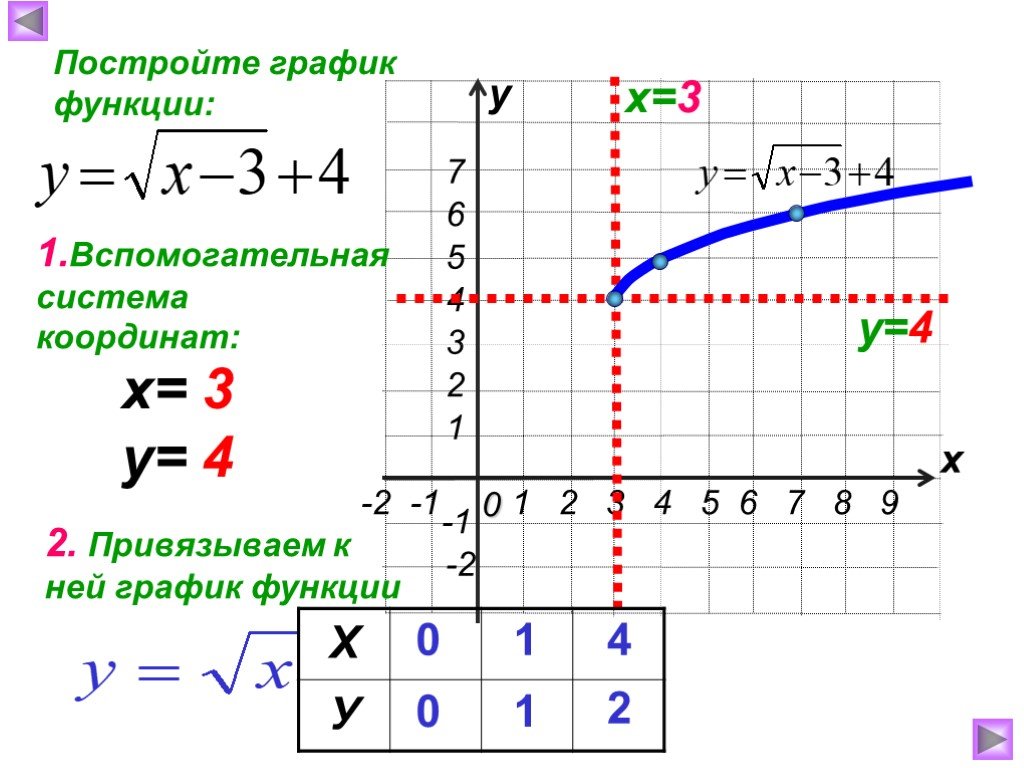
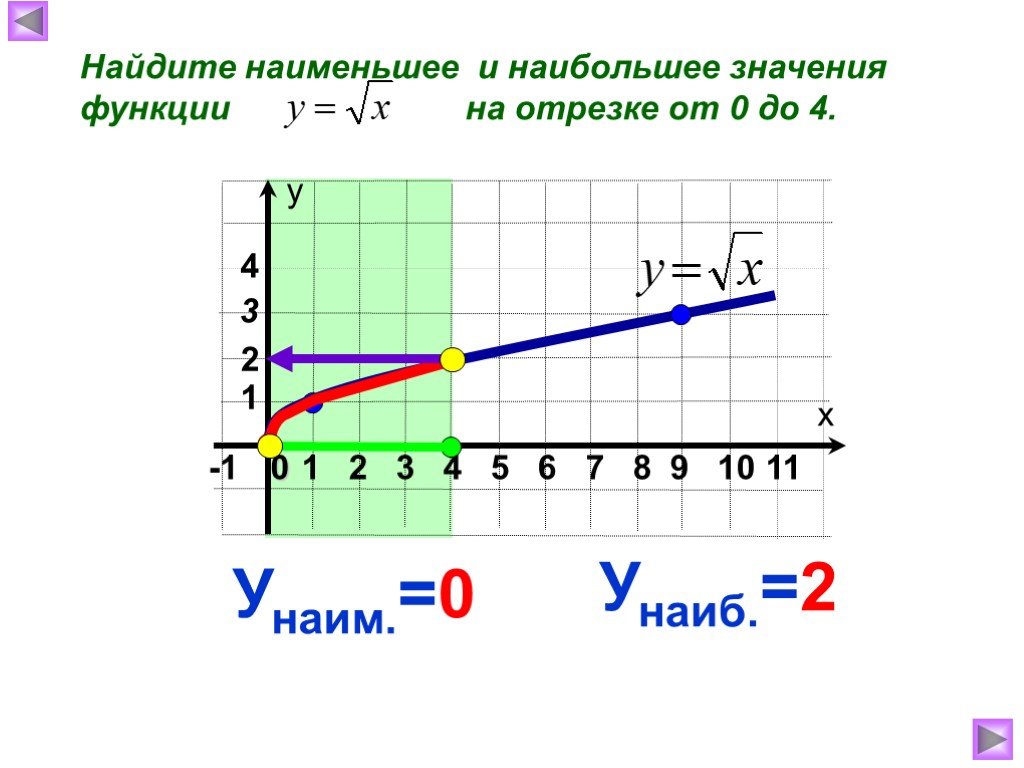
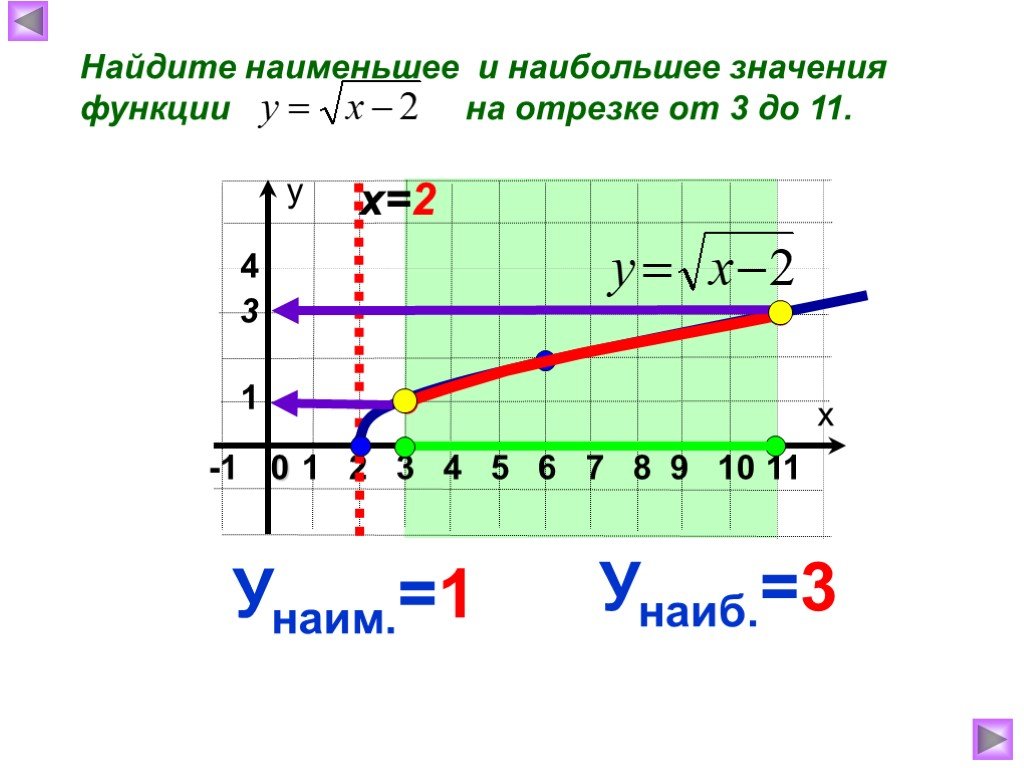
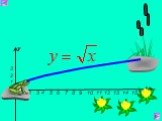
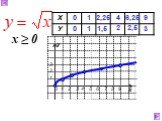
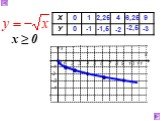
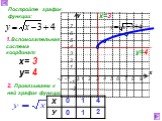
Презентация "Функция арифметического квадратного корня, её свойства" по математике – проект, доклад

Скачать презентацию (0.72 Мб) Смотреть похожие презентации Конспекты для презентации

Слайд 1

Слайд 2

Слайд 3

Слайд 4

Слайд 5

Слайд 6

Слайд 7

Слайд 8

Слайд 9

Слайд 10

Слайд 11

Слайд 12

Слайд 13

Слайд 14

Презентацию на тему "Функция арифметического квадратного корня, её свойства" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 14 слайд(ов).

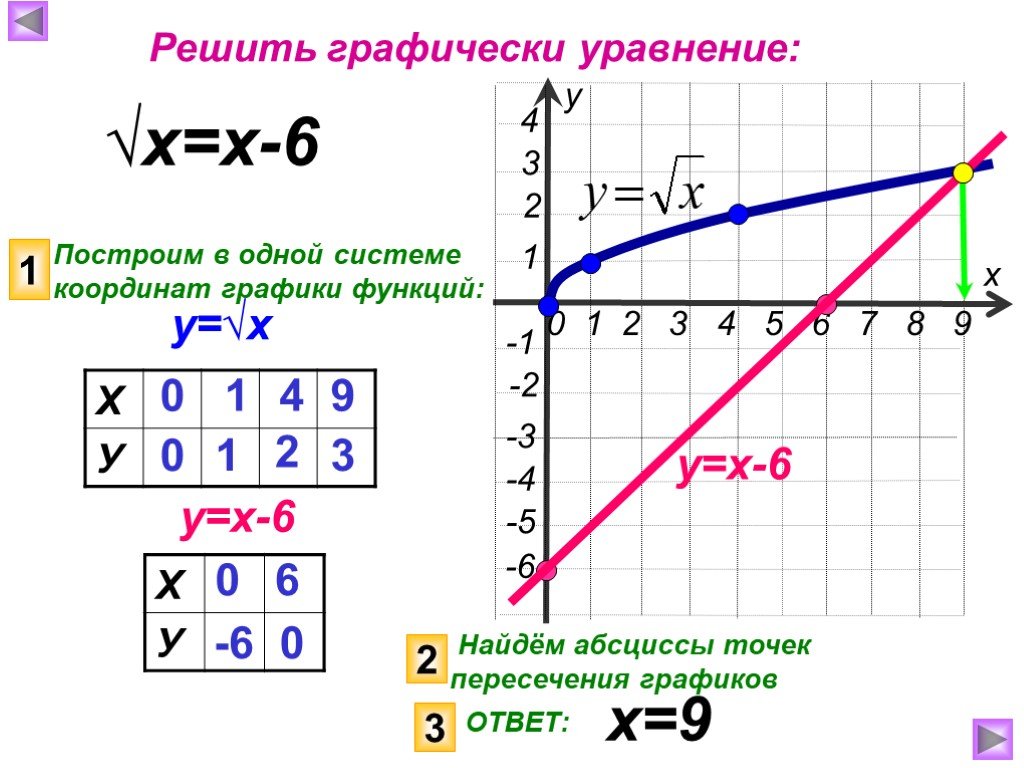
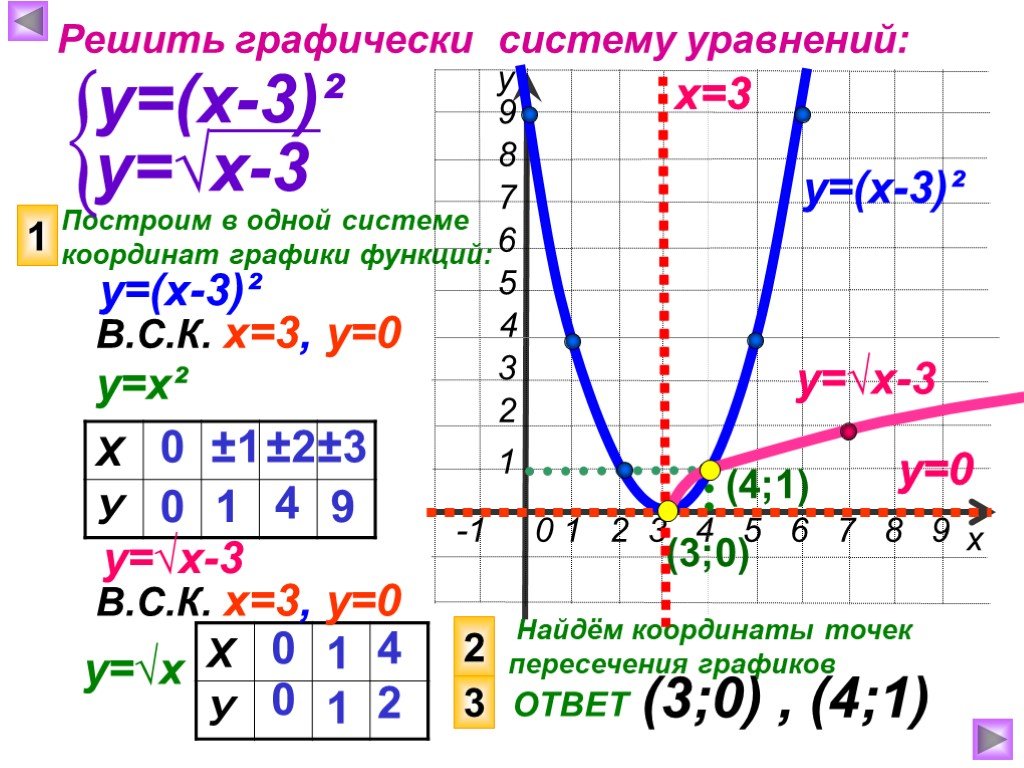
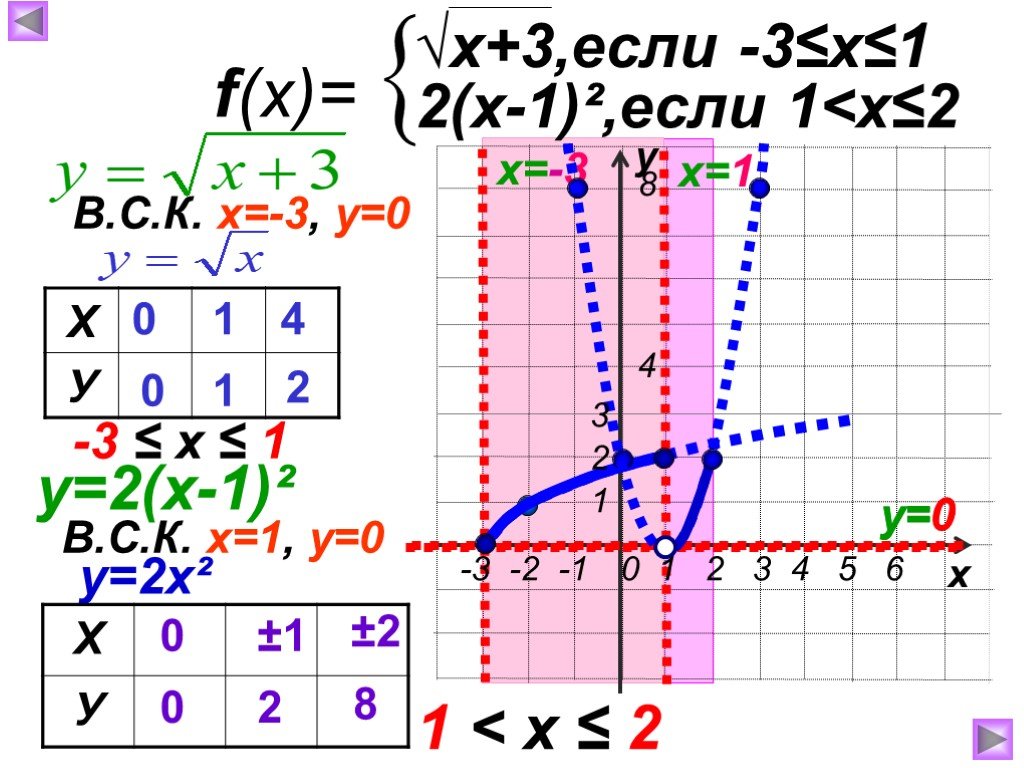
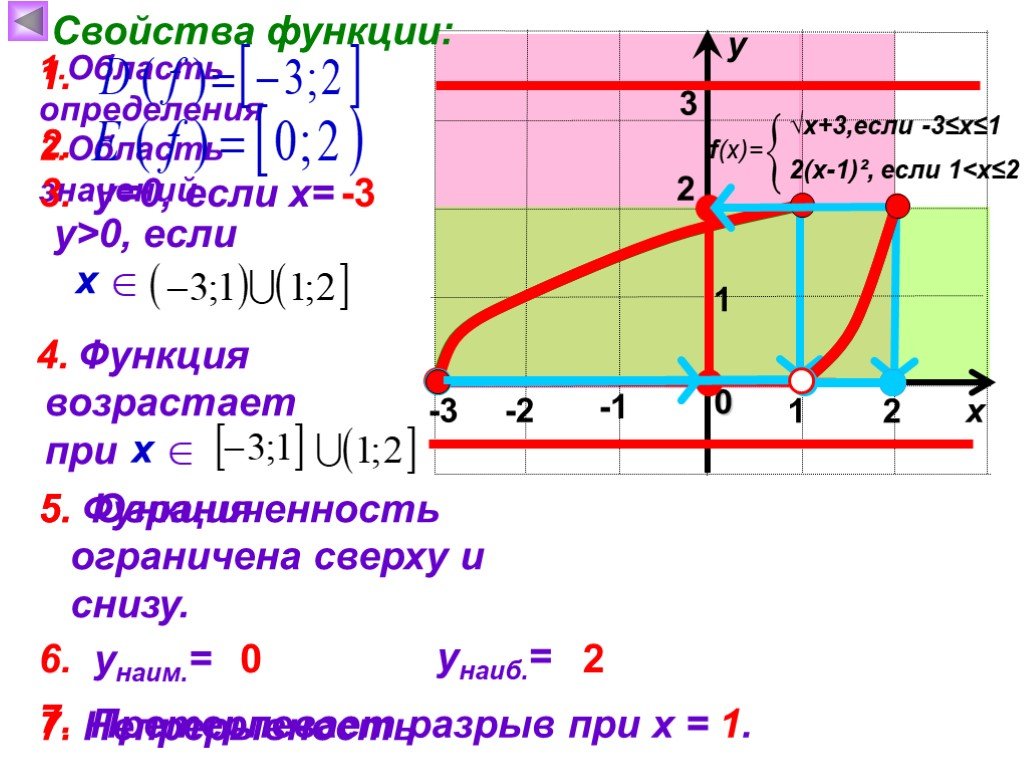
Скачать презентацию (0.72 Мб) Смотреть похожие презентации Конспекты для презентации

Слайды презентации

Слайд 1

Функция ,

её свойства и график.

8 класс учебник Мордковича А. Г.

Ткаченко И. В. гимназия №5 г. Мурманск

Слайд 2

Слайд 3

0 1 4 2 6,25 2,5 9 2,25 1,5 х ≥ 0

Слайд 4

7. Непрерывна.

Функция возрастает при

Функция ограничена снизу, но не ограничена сверху.

Свойства функции у=√х:

1.Область определения

2.Область значений

3. у=0, если х= у>0, если 5. Ограниченность 5. 6. унаим.= унаиб.= НЕТ 7. Непрерывность

Слайд 5

-1 -2 -3

Слайд 6

Функция убывает при

Функция ограничена сверху, и не ограничена снизу.

Свойства функции у=-√х:

у<0, если

Слайд 7

х у

Постройте график функции:

х=3 у=4

1.Вспомогательная система координат:

2. Привязываем к ней график функции

х= 3 у= 4

Слайд 8

Найдите наименьшее и наибольшее значения функции на отрезке от 0 до 4.

Унаиб.=2 Унаим.=0

Слайд 9

Найдите наименьшее и наибольшее значения функции на отрезке от 3 до 11.

х=2 Унаиб.=3 Унаим.=1

Слайд 10

у=√х √х=х-6

Построим в одной системе координат графики функций:

у=х-6 -6 6

Найдём абсциссы точек пересечения графиков

3 ОТВЕТ: х=9

Решить графически уравнение:

Слайд 11

Решить графически систему уравнений:

у=(х-3)² у=√х-3

Найдём координаты точек пересечения графиков

ОТВЕТ (3;0) , (4;1) у=0 (3;0) ±1 ±2 ±3 у=х² В.С.К. х=3, у=0 (4;1)

f(x)=. Постройте график функции и опишите её свойства. √x+3,если -3≤х≤1 2(х-1)²,если 1

Слайд 12

f(x)=

Постройте график функции и опишите её свойства.

√x+3,если -3≤х≤1 2(х-1)²,если 1<х≤2

Слайд 13

х=-3 В.С.К. х=-3, у=0 у=2(х-1)² -3 ≤ х ≤ 1 В.С.К. х=1, у=0 х=1 у=2х² 8 1 < х ≤ 2

Слайд 14

Функция ограничена сверху и снизу.

Свойства функции:

Претерпевает разрыв при х = 1.

1 2

Список похожих презентаций

Свойства арифметического квадратного корня

Куда: г. Стерлитамак, МБОУ «СОШ №8» Кому: 8 классу. Прочитайте выражения:. х+75 (15-8)+у 34-(х+10) (а-12)-(х-86) (х-у)-(7+а) (у+99)+(76-4) (25+у)-х ...

Свойства арифметического квадратного корня

План урока. Организационный момент. Теоретический устный опрос. Расшифруй поговорку. Найди ошибку. Работа в группах. Проблемные ситуации. Итог урока. ...

Квадратичная функция, её свойства и график

Цели:. ввести понятие квадратичной функции; научится строить график функции у=ах2 + ах +с и описывать свойства данной функции по графику; установить ...

Квадратичная функция, её свойства и график

Определение. Квадратичной функцией называется функция, которую можно задать формулой вида y = ax2 + bx + c, где x – независимая переменная, a,b и ...

Квадратичная функция. Её свойства и график

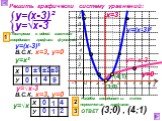
Определение квадратичной функции. Функцию вида y = ax2 + bx + c, где a, b, c - произвольные числа, причём a ≠ 0, называют квадратичной функцией («a» ...

I Функция У=АХ², её график и свойства

А=1 У=Х ². А=2 У=2Х ². У=Х² У=2Х². Растяжение от оси Х в два раза. А=0.5 У=Х² У=0.5Х². Сжатие по оси Х в два раза. Вообще график функции У=АХ² можно ...

Показательная функция и её свойства

Показательная функция. В практике часто используются функции y=2x, y=10x, y=(0,1)x и т. д., т. е. функция вида y=ax где а - заданное число, x -переменная. ...

Показательная функция, её свойства и график

. Рост древесины происходит по закону, где: A- изменение количества древесины во времени; A0- начальное количество древесины; t-время, к, а- некоторые ...

Квадратичная функция, её свойства и график

Вспомнить свойства функций у = kx +b и у = х², их графики. Изучить свойства функции у = kx², у = - kx² и научиться строить график. Научиться по графику ...

"Функция y = kx², ее свойства и график". 8-й класс

Траектория движения комет в межпланетном пространстве. Архитектурные сооружения. . Траектория движения. Тема урока. Функция у=кх2, ее график и свойства ...

Извлечение квадратного корня из четырёх- и трёхзначного числа

План действий: Найти квадрат числа для числа (№1), составленного из цифр тысяч (если такая есть) и сотен данного числа. Записать найденное число за ...

Преобразование выражений, содержащих операцию извлечения квадратного корня

Основные свойства квадратного корня из неотрицательного числа. ? Тема:Преобразование выражений, содержащих операцию извлечения квадратного корня. ...

Определение арифметического корня п-ой степени

Повторение:. 1) Имеет ли смысл выражение:. ? 2) Докажите, что:. Число 5 есть корень третьей степени из 125. т. к. Число 0 есть корень восьмой степени ...

Показательная функция и ее свойства

"Дорогу осилит идущий, а математику - мыслящий". Вопросы: Независимая переменная (х) Наглядный способ задания функции (графический) График четной ...

Показательная функция, ее свойства и график

Определение показательной функции. Показательной функцией называется функция у = а , где а – заданное число, а>0, a ≠ 1. х Примеры:. График показательной ...

Логарифмическая функция, ее свойства и график

Назвать функции, заданные формулами и соответствующие им графики. Свойства функции:. область определения функции область значений функции четность ...

Показательная функция, ее свойства и график

Свойства показательной функции:. Функцию вида y=ax, где а>0, a≠1, х – любое число, называют показательной функцией. Область определения показательной ...

Линейная функция и её график

Цель урока: Сформировать представление о числовой функции на примере линейной функции, с её графиком и алгоритмом его построения по двум точкам. ЗАДАЧИ: ...

Квадратичная функция и ее свойства

Определение. Функция вида у = ах2+bх+с, где а, b, c – заданные числа, а≠0, х – действительная переменная, называется квадратичной функцией. Примеры: ...

Квадратный трехчлен. Квадратичная функция. Квадратные уравнения. Разложение квадратного трехчлена на множители

Разработано учителем математики МОУ «СОШ» п. Аджером Корткеросского района Республики Коми Мишариной Альбиной Геннадьевной. Содержание. Квадратный ...

Конспекты

Советы как сделать хороший доклад презентации или проекта

Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
Старайтесь говорить уверенно, плавно и связно.
Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.