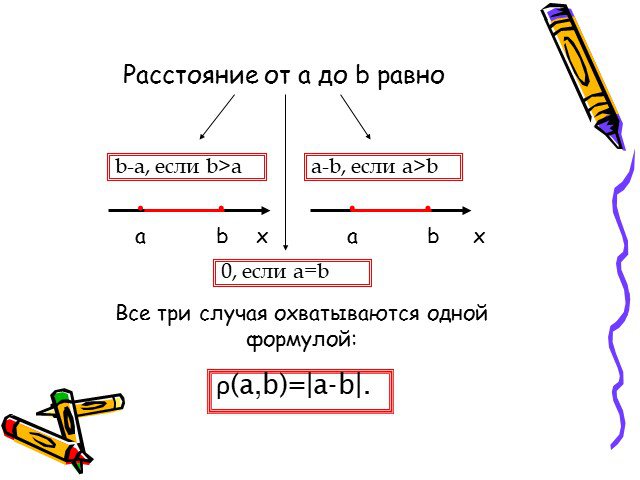
Презентация "Геометрический смысл модуля действительного числа" по математике – проект, доклад

Скачать презентацию (48 Кб) Смотреть похожие презентации Конспекты для презентации

Слайд 1

Слайд 2

Слайд 3

Слайд 4

Слайд 5

Слайд 6

Презентацию на тему "Геометрический смысл модуля действительного числа" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 6 слайд(ов).

Скачать презентацию (48 Кб) Смотреть похожие презентации Конспекты для презентации

Слайды презентации

Слайд 1

Геометрический смысл модуля действительного числа

Выполнила ученица 8 класса Коковихина Анастасия

Слайд 2

Расстояние от a до b равно

х a b b-a, если b>a a-b, если a>b 0, если a=b ρ(a,b)=|a-b|.

Все три случая охватываются одной формулой:

Слайд 3

решим уравнения:

а) |x-2|=3 Найдём на координатной прямой такие точки х, которые удовлетворяют условию ρ(х,2)-3, т. е. удалены от точки 2 на расстояние, равное 3. Это – точки – 1 и 5. Следовательно уравнение имеет два корня: -1 и 5

-1 5 2

Слайд 4

б) |х-√2|=0 Для уравнения |х-√2|=0 можно обойтись без геометрической иллюстрации, ведь если |а|=0, то а=0. поэтому х-√2=0, т. е. x=√2.

Слайд 5

в) |2х-6| = 8 |2х-6| = |2х(х-3)| = |2|∙|х-3| = 2|х-3|. Значит, заданное уравнение можно преобразовать к виду 2|х-3| = 8, откуда получаем |х-3| = 4. Нам нужно найти такие точки, которые отдалены от точки 3 на расстояние, равное 4.Это – точки -1 и 7. Итак, уравнение имеет два корня: -1 и 7.

Слайд 6

Спасибо за внимание!

Список похожих презентаций

Геометрический смысл производной

Геометрическая интерпретация производной, впервые данная в конце XVII в. Лейбницем, который основываясь на результатах Ферма и некоторых других выводах, ...

Геометрический смысл производной функции

Рано или поздно всякая правильная математическая идея находит применение в том или ином деле. А.Н.Крылов. Цель урока. 1) выяснить, в чем состоит геометрический ...

Модуль действительного числа

Цели и задачи урока. Ввести определение модуля действительного числа, рассмотреть свойства и разъяснить геометрический смысл модуля; Ввести функцию ...

Нахождение числа по его дроби

Мы часто находим часть от числа или наоборот, вычисляем число по его части:. Например: Сколько будет 1/2 от 5 км? Понятно, что полпути – это 2,5 км. ...

Нахождение дроби от числа и числа по его дроби

I.Прочитай задачи, запиши краткое условие, реши задачи. II.Cоставь свою стратегию решения задач. 1.Масса вяленой рыбы составляет 55% массы свежей ...

Натуральные числа в жизни людей

НАТУРАЛЬНЫЕ ЧИСЛА. С НАТУРАЛЬНЫМИ ЧИСЛАМИ Я ПОЗНАКОМИЛСЯ ЕЩЕ В РАННЕМ ДЕТСТВЕ. МАМА НАРИСОВАЛА ИХ НА ВАТМАНЕ И ПРИКРЕПИЛА К СТЕНЕ. ЦИФРЫ НА ПЛАКАТЕ ...

Наибольший общий делитель. Взаимно простые числа

Устная работа. 1. Вычислите: а) 0,7∙10 : 2 - 0,3 : 0,4 ? б) 5 :10 ∙0,2 +2 :0,7 ? 2. Опровергните утверждение: «Число 2 является общим делителем всех ...

Колдовские числа

С давних времен люди воспринимали число как божественное начало, сущность мира. В исследованиях числовых отношений видели они средство спасения души, ...

Конкретный смысл деления

Расставьте знаки арифметический действий:. 50 - 42 + 3 = 11 69 + 11 - 57 = 23 11 - 0 + 11 = 22 *. Расшифруйте ребусы:. опять семьсот пистолет трибуна ...

Взаимно обратные числа

Дать определение взаимно обратных чисел; Научить находить числа, обратные данным, представленных в виде смешанных чисел, десятичных дробей. Цели и ...

Взаимно обратные числа

...

Арабские цифры и числа

. ...

Взаимно обратные числа

Цель урока:. дать определение взаимно обратных чисел. научить находить число, обратное данному. развивать логическое мышление. Развитие логического ...

Анализ контрольной работы по математике на тему "Натуральные числа и шкалы"

Натуральные числа и шкалы. 5 к л а с с № 1. Цели деятельности учителя. Главная дидактическая цель : организовать деятельность учащихся, направленную ...

Алгебра модуля

АЛГЕБРА МОДУЛЯ. Решение уравнений с модулем. Решение неравенств с модулем. Построение графиков с модулем. Построение с помощью Преобразования графиков. ...

«Моя математика» 1- класс - числа 0-10

Цели урока: Закрепить: навыки счета в пределах10; состав чисел 2-10; умение записывать числа арабскими и римскими цифрами; умение сравнивать выражения; ...

"Смешанные дроби. Представление смешанного числа в виде неправильной дроби".

Смешанные дроби. Представление смешанного числа в виде неправильной дроби. 02.03. Определите координаты точек А, В, С и М. ...

Взаимно простые числа

В СТРАНЕ СМЕШАРИКОВ. оглавление. ЦЕЛИ И ЗАДАЧИ ПЛАН УРОКА ИТОГИ ДОМАШНЕЕ ЗАДАНИЕ ТЕМА УРОКА ОБОРУДОВАНИЕ. тема урока. взаимно простые числа. план ...

Квадрат и куб числа

Прочитайте выражения. 3 * 3 5 * 5 6 * 6. Эти выражения в буквенной форме имеют вид n * n. Произведение n * n называют квадратом n числа и обозначают ...

Возведение в степень. Куб и квадрат числа

Устно. Упростить выражение: 25х + 15 х; 12у – 3у; 9k + 9k – 4k; 80c-35c-14c; 8d+d-9d; 163 + 37v + 18v. Решить уравнение: 7х+2х = 918; 5а-3а = 222; ...

Конспекты

Советы как сделать хороший доклад презентации или проекта

Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
Старайтесь говорить уверенно, плавно и связно.
Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.