Презентация "Геометрический смысл производной" по математике – проект, доклад
Презентацию на тему "Геометрический смысл производной" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 11 слайд(ов).
Слайды презентации
Список похожих презентаций
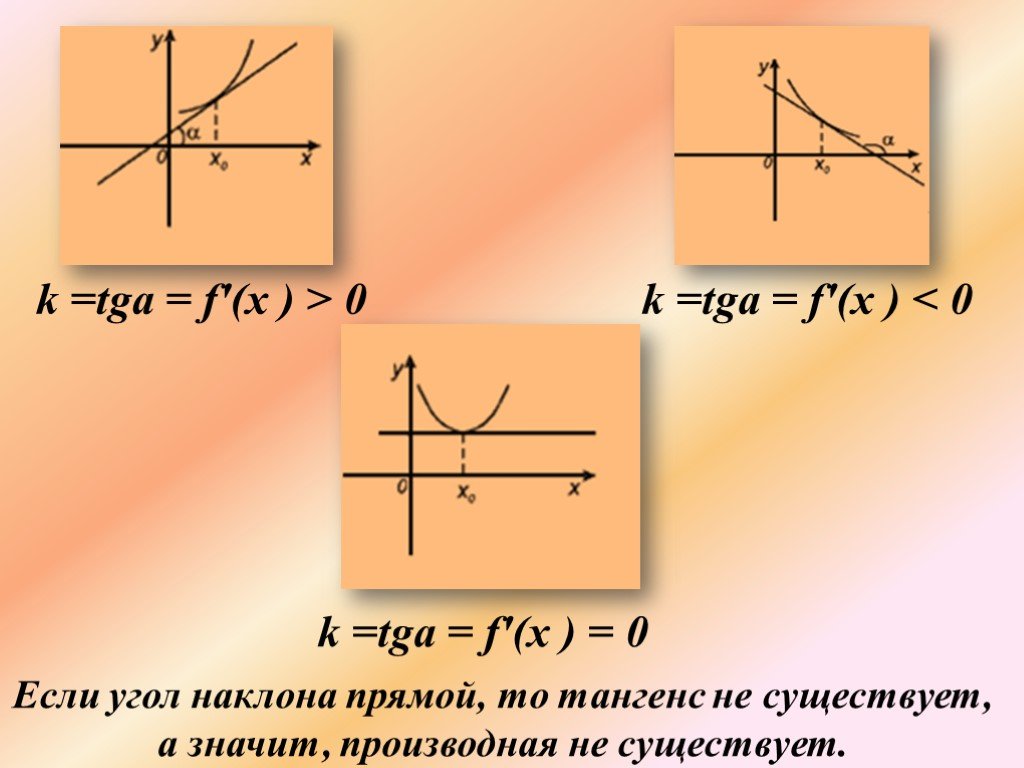
Геометрический смысл производной функции
Рано или поздно всякая правильная математическая идея находит применение в том или ином деле. А.Н.Крылов. Цель урока. 1) выяснить, в чем состоит геометрический ...Производная функции. Геометрический смысл производной
Производная функции — одна из сложных тем в школьной программе. Не каждый выпускник ответит на вопрос, что такое производная. Производная. — это скорость ...Физический и геометрический смысл производной
Производной функции называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю:. Производная ...Экономический смысл производной
ИМЯ УРОКА. «Успех порождает успех!». Девиз дня: «Если мы действительно что-то знаем, то мы знаем это благодаря изучению математики» (Пьер Гассенди). ...Геометрический смысл модуля действительного числа
Расстояние от a до b равно. х a b b-a, если b>a a-b, если a>b 0, если a=b ρ(a,b)=|a-b|. Все три случая охватываются одной формулой:. решим уравнения:. ...Физический смысл производной
f ' (x0) = lim (∆ f / ∆x) ∆x→ 0. Пусть х - произвольная точка, лежащая в некоторой окрестности точки Х0 (окрестность точки Х0 - это интервал (а; b), ...Применение производной к исследованию функции
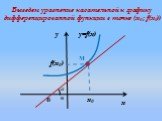
Применение производной к исследованию функции. Критические точки функции. х у у = g (х) у = f (х). Повторение: описание свойств функции по её графику ...Применение производной в физике
В математике следует помнить не формулы, а процессы мышления. В.П. Ермаков. Урок № 1 повторительно-обобщающий. Производная и ее применение при решении ...Применение производной для исследования функций
Монотонность функции. Убывает на (-;x, x) Возрастает на х1; х2. Постоянна на а;в. у х У=f(x) x1 а в. Исследование функции на возрастание. ...Применение производной
Функция НЕ функция. у а б 2 Графики функций. . Возрастание и убывание функции. Иду в гору. Функция возрастает на промежутке[b;a]. Иду под гору. Функция ...Применение производной в естествознании
Из истории создания. Первые задачи на максимум и минимум были поставлены в V веке до н.э. Евклид, Архимед, Кеплер, Герон, Ферма решали эти задачи ...Геометрический сундучок
Фундаментальные понятия. Определения. Свойства геометрических фигур. Теоремы. Фундаментальные (неопределяемые)понятия. Точка Прямая Плоскость. Назад ...Приложения производной
Правильному применению методов можно научиться только применяя их на разнообразных примерах. Цейтен Г.Г. Тема урока: Приложения производной. Чтение ...Исследование функции с помощью производной
Исследование функции с помощью производной. УСТНЫЙ ОПРОС. Достаточный признак возрастания функции. Достаточный признак убывания функции. Какие точки ...Конкретный смысл действия умножения
Цели урока. Углубить знание конкретного смысла действия умножения. Учить проводить исследования, составлять и решать задачи, примеры, тесты. Развивать ...Исследование функции производной
Цели урока: выяснение степени усвоения . правил вычисления производных; дать понятие «промежутка монотонности функции» уметь применять производную ...Исследование функции с помощью производной
Правила дифференцирования. Производная суммы равна сумме производных. Постоянный множитель можно вынести за знак производной. Производная произведения ...Задачи, приводящие к понятию производной
=x0+∆x. Приращение функции и приращение аргумента. y=f(x) x0 f(x)=f(x0+∆x) f(x0) ∆x ∆f. приращение аргумента:. x y ∆х = х - х0 (1). Приращение функции ...Задачи на нахождение производной степенной функции
Повторение опорного материала: а) теоретическая часть. Что называется производной функции у(х) ? Сформулируйте правила дифференцирования Запишите ...Конспекты
Производная. Геометрический смысл производной. Применение производной к исследованию функции. Задачи В-8
Государственное общеобразовательное учреждение. Гимназия №205. Урок по теме. « Производная. Геометрический смысл производной. Применение ...Геометрический смысл производной. Применение производной к исследованию функций
Урок- консультация по теме «Геометрический смысл производной. Применение производной к исследованию функций». Цель урока. :. содействовать созданию ...Геометрический смысл производной
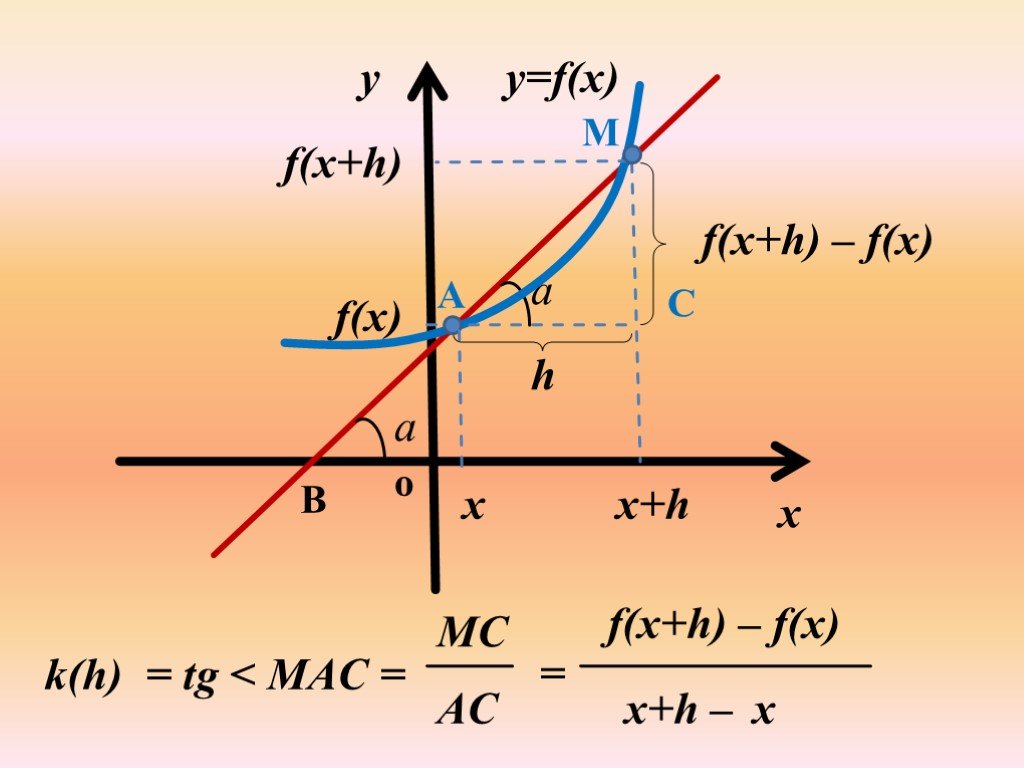
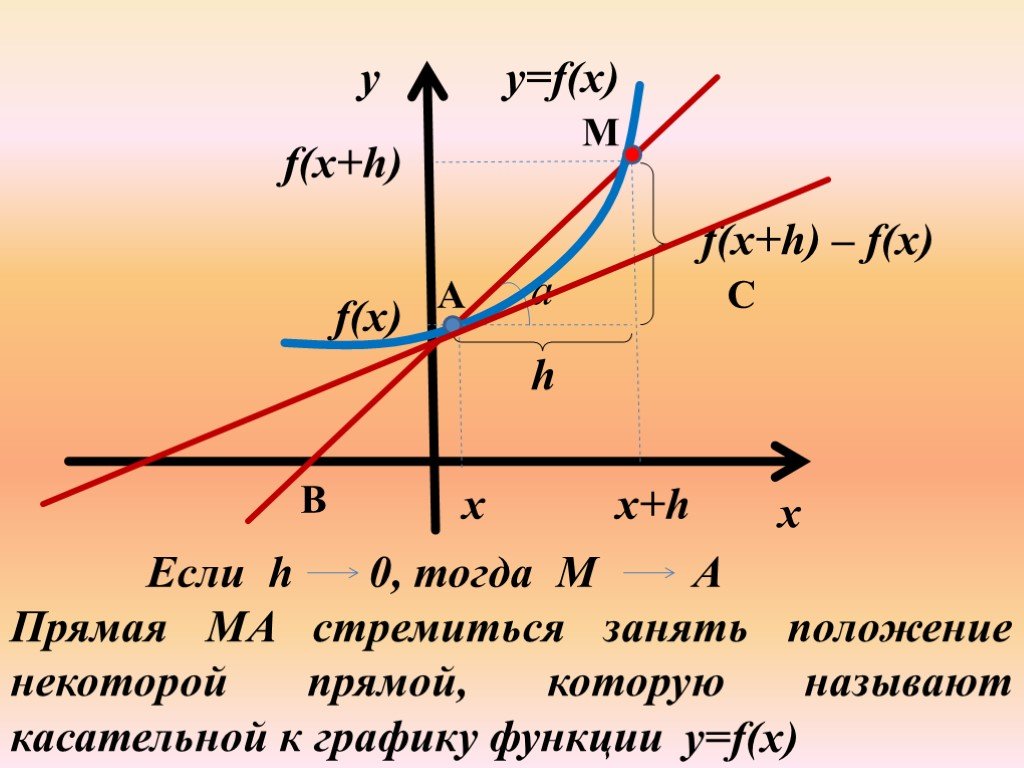
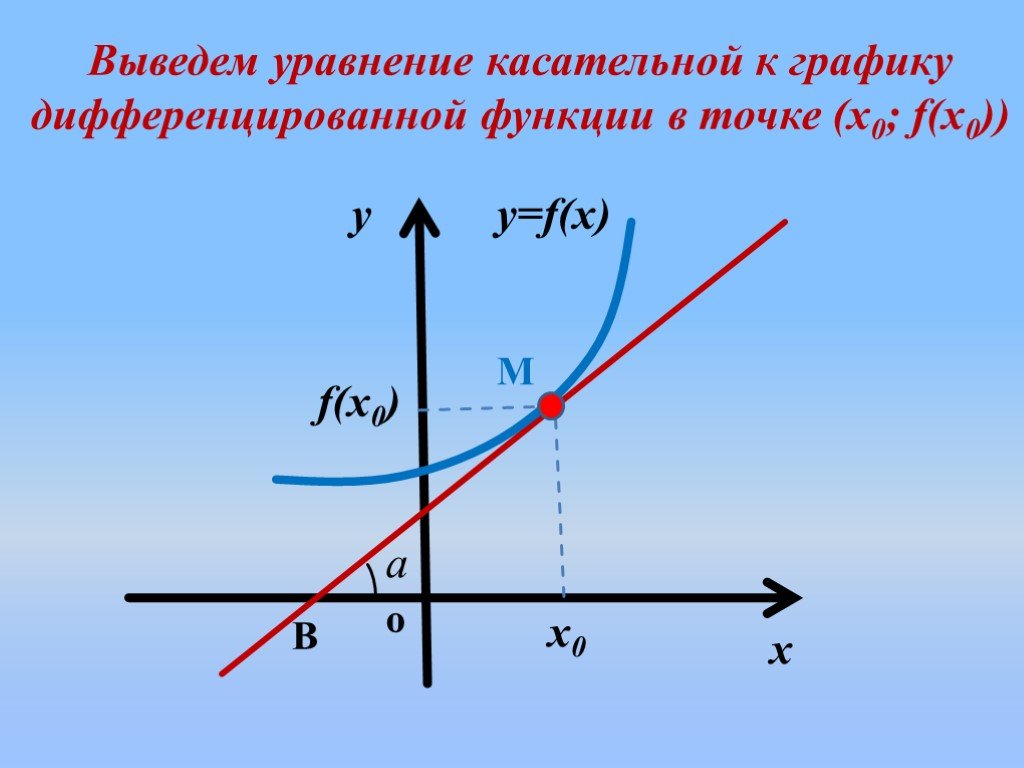
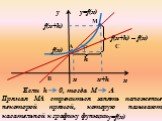
Тема: Геометрический смысл производной (В8 и В14 в ЕГЭ). Цель урока:. . Выяснить, в чем состоит геометрический смысл производной, уравнения касательной ...Геометрический смысл производной
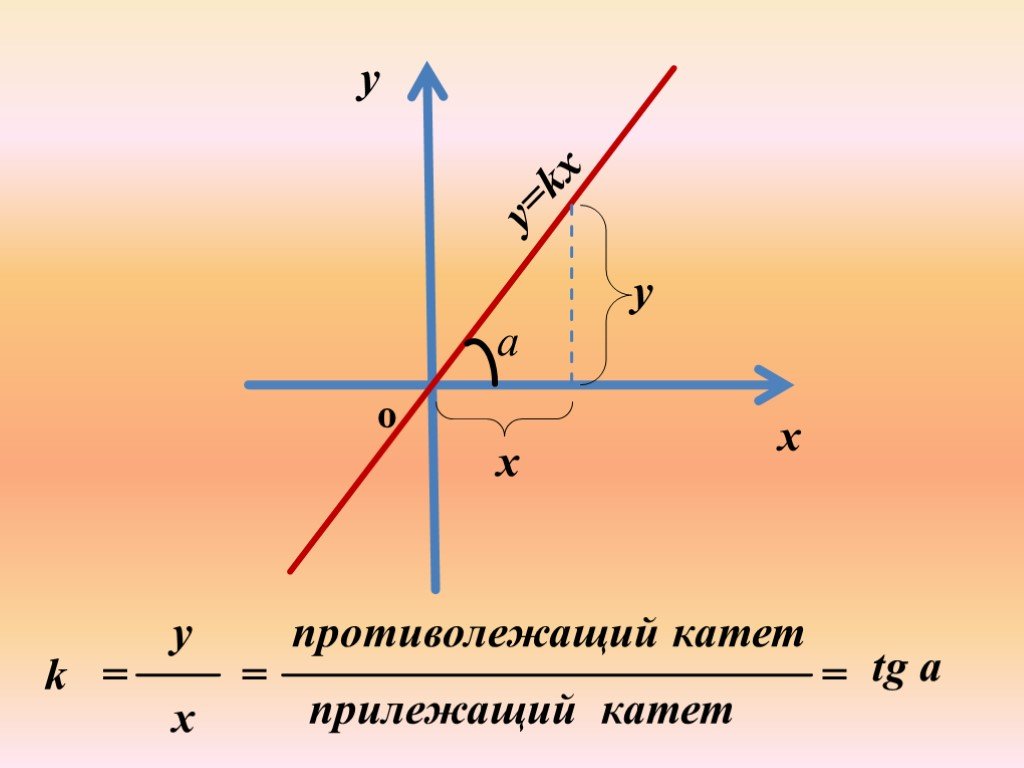
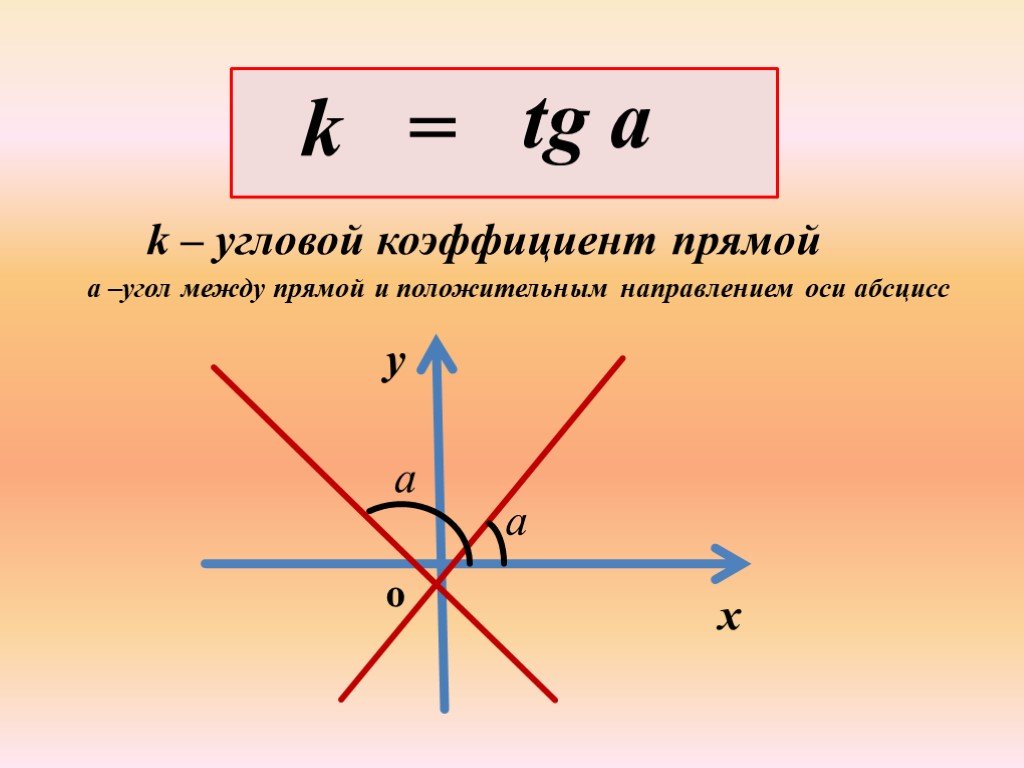
Открытый урок по теме:. «Геометрический смысл производной». Цели урока. : дать понятие углового коэффициента прямой, определение угла между прямой ...Производная.Геометрический и физический смысл производной
Муниципальное бюджетное общеобразовательное учреждение средняя общеобразовательная школа № 17 село Краснопартизанское. Урок разноуровневого ...Геометрический и физический смысл производной. Применение производной
Учитель математики. КГУ «Экономический лицей». Воробьева. Ирина. Юрьевна. Методическая разработка. урока математики в 10 классе. « Геометрический ...Производная Геометрический и физический смысл производной
Муниципальное бюджетное общеобразовательное учреждение средняя общеобразовательная школа № 17 село Краснопартизанское. Урок по алгебре. для ...Производная. Геометрический и механический смысл производной
Тема. . Производная. Геометрический и механический смысл производной. . . Цель. . Повторить, о. бобщить и систематизировать материал по ...Понятие о производной функции. Ее геометрический и физический смысл
Дата. . Класс. . Предмет. . . 14.11.2013. . . 11. . Алгебра и начала анализа. . . . Тема урока:. Понятие о производной ...Производная. Физический и геометрический смыл производной
Лебедева Ирина Анатольевна, учитель математики МБОУ Новобатайская СОШ №9. . Тема «Производная. Физический и геометрический смыл производной». ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:8 декабря 2018
Категория:Математика
Содержит:11 слайд(ов)
Поделись с друзьями:
Скачать презентацию