Презентация "Задачи, приводящие к понятию производной" по математике – проект, доклад

ОПРЕДЕЛЕНИЕ ПРОИЗВОДНОЙ

1. Задачи, приводящие к понятию производной

Составила учитель математики МОУ «Гимназия им. Горького А.М.»: Фабер Г.Н.

=x0+∆x

Приращение функции и приращение аргумента

y=f(x) x0 f(x)=f(x0+∆x) f(x0) ∆x ∆f

приращение аргумента:

x y ∆х = х - х0 (1)

Приращение функции :

∆f = f(x0 +∆x)-f(x0) (2) ∆f = f(x)-f(x0) (3)

В окрестности точки х0 возьмём точку х

Пусть х0- фиксированная точка, f(х0)- значение функци в точке х0

Расстояние между точками х и х0 обозначим ∆х.Оно называется приращением аргумента и равно разности между х и х0:

Первоначальное значение аргумента получило приращение ∆х, и новое значение х равно х0+∆х

Функция f(х) тоже примет новое значение: f(x0+∆x)

Т.е., значение функции изменилось на величину f(x)-f(x0)= f(x0 +∆x)-f(x0),КОТОРАЯ НАЗЫВАЕТСЯ ПРИРАЩЕНИЕМ ФУНКЦИИ И ОБОЗНАЧАЕТСЯ ∆f

Дана функция f(x)

Задача 1 (о скорости движения).

По прямой, на которой заданы начало отсчета, единица измерения (метр) и направление, движется некоторое тело (материальная точка). Закон движения задан формулой s=s (t), где t — время (в секундах), s (t) — положение тела на прямой (координата движущейся материальной точки) в момент времени t по отношению к началу отсчета (в метрах). Найти скорость движения тела в момент времени t (в м/с).

Предположим, что в момент времени t тело находилось в точке М пройдя путь от начала движения ОМ = s{t). Дадим аргументу t приращение ∆t и рассмотрим момент времени t+∆t Координата материальной точки стала другой, тело в этот момент будет находиться в точке P : OP=s(t+∆t) Значит, за ∆t секунд тело переместилось из точки М в точку Р, т.е. прошло путь МР. Имеем: MP=OP-OM=s(t+∆t)-s(t)=∆s Полученную разность мы назвали в § 26 приращением функции Путь ∆s тело прошло за ∆t секунд. Нетрудно найти среднюю скорость движения тела за промежуток времени [t;t+∆t] : = А что такое скорость v (t) в момент времени t (ее называют иногда мгновенной скоростью)? Можно сказать так: это средняя скорость движения за промежуток времени [t;t+∆t] при условии , что ∆t выбирается все меньше и меньше; точнее: иными словами, при условии, что ∆t→0.Это значит , что Подводя итог решению задачи 1, получаем:

Задача 2

Поднимем камешек и затем из состояния покоя отпустим его. Движение свободно падающего тела явно неравномерное. Скорость v постепенно возрастает. Но как именно выглядит зависимость v(t) ?

Фиксируем момент t, в который мы хотим знать значение скорости v(t). Пусть h – небольшой промежуток времени, прошедший от момента t. За это время падающее тело пройдёт путь, равный s(t+h)-s(t). Если промежуток времени h очень мал, то приближённо s(t+h)-s(t)≈v(t)∙h, или , причём последнее приближённое равенство тем точнее, чем меньше h. Значит величину v(t) скорости в момент t можно рассматривать как предел, к которому стремится отношение, выражающее среднюю скорость на интервале времени от момента t до момента t+h. Сказанное записывают в виде

Прямая, проходящая через точку М0 (х0; f(х0)), с отрезком которой почти сливается график функции f(х),называют касательной к графику в точке х0

M0 X

Тема: Задача, приводимая к понятию “производная”

0

Задача: Определить положение касательной (tgφ)

х у М0 х0 М f(x) =f(x0+∆x)  φ

Секущая, поворачиваясь вокруг точки М0, приближается к положению касательной

Предельным положением секущей МоМ, когда М неограниченно приближается к Мо, является касательная

Пусть дан график функции f(х) и касательная, проходящая через точку М0 ,которая образует с положительным направлением оси ОХ угол φ

Отметим точку М, координаты которой рассмотрим как приращение координат точки М0

Через точки М и М0 проведём секущую, которая образует с осью ОХ угол 

Будем перемещать точку М вдоль графика, приближая её к точке М0.Соответственно будет меняться положение секущей ММ0

При этом координата х точки М будет стремиться к х0

К чему будет стремиться приращение аргумента?

А к какому углу будет стремиться угол  ?

Задача о касательной к графику функции

С ∆х=х-х0 ∆f(x) = f(x) - f(x0)

Задача о мгновенной величине тока

Обозначим через q = q(t) количество электричества, протекающее через поперечное сечение проводника за время t. Пусть Δt – некоторый промежуток времени, Δq = q(t+Δt) – q(t) – количество электричества, протекающее через указанное сечение за промежуток времени от момента t до момента t + Δt. Тогда отношение называют средней силой тока. Мгновенной силой тока в момент времени t называется предел отношения приращения количества электричества Δq ко времени Δt, при условии, что Δt→0.

Выводы

Различные задачи привели в процессе решения к одной и той же математической модели – пределу отношения приращения функции к приращению аргумента при условии, что приращение аргумента стремится к нулю. Значит, эту математическую модель надо специально изучить, т.е.: Присвоить ей новый термин. Ввести для неё обозначение. Исследовать свойства новой модели. Определить возможности применения нового понятия - производная

Задача о скорости химической реакции

Средняя скорость растворения соли в воде за промежуток времени [t0;t1] (масса соли, растворившейся в воде изменяется по закону х = f(t)) определяется по формуле . Скорость растворения в данный момент времени

Определение производной

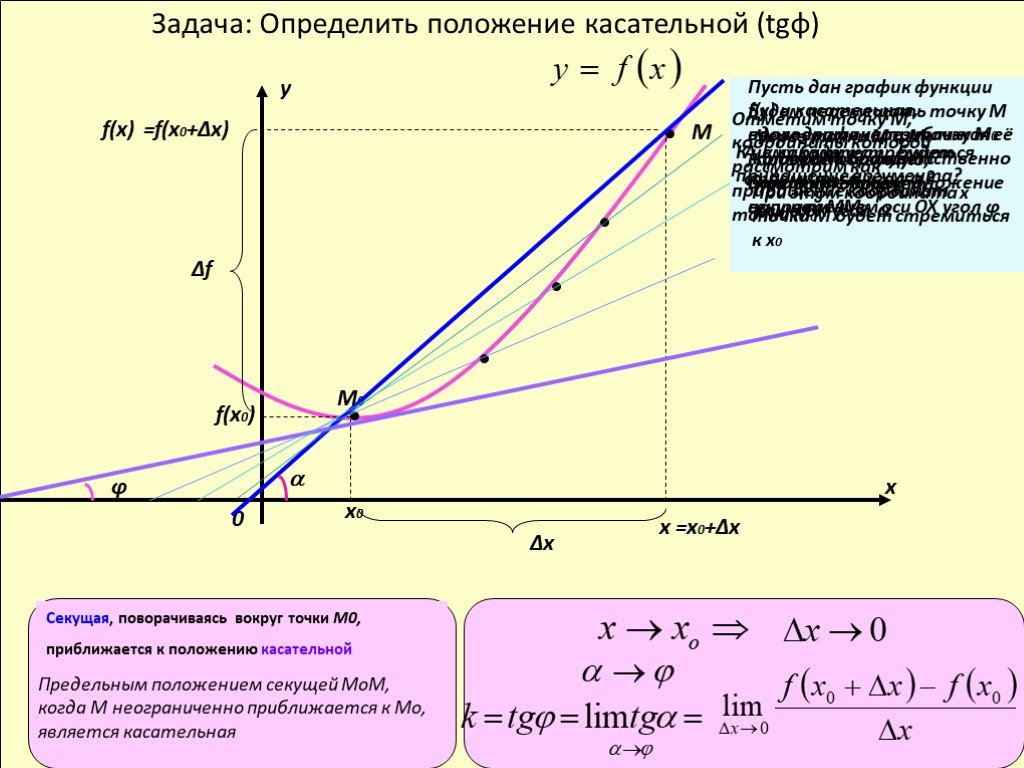
Производной функции f в точке х0 называется предел отношения приращения функции к приращению аргумента при последнем стремящимся к нулю:

Возвращаясь к рассмотренным задачам, важно подчеркнуть следующее: а) мгновенная скорость неравномерного движения есть производная от пути по времени; б) угловой коэффициент касательной к графику функции в точке (x0; f(x)) есть производная функции f(x) в точке х = х0; в) мгновенная сила тока I(t) в момент t есть производная от количества электричества q(t) по времени; Г) скорость химической реакции в данный момент времени t есть производная от количества вещества у(t), участвующего в реакции, по времени t.

А л г о р и т м

1) ∆x = x – x0 2) ∆f = f(x+x0) – f(x0) 3) 4)

А это значит:

Аппарат производной можно использовать при решении геометрических задач, задач из естественных и гуманитарных наук, экономических задач оптимизационного характера. И, конечно, не обойтись без производной при исследовании функции и построении графиков, решении уравнений и неравенств

«…нет ни одной области в математике, которая когда-либо не окажется применимой к явлениям действительного мира…» Н.И. Лобачевский

Основные формулы

Средняя скорость = Мгновенная скорость или Скорость изменения функции Значение производной в точке =