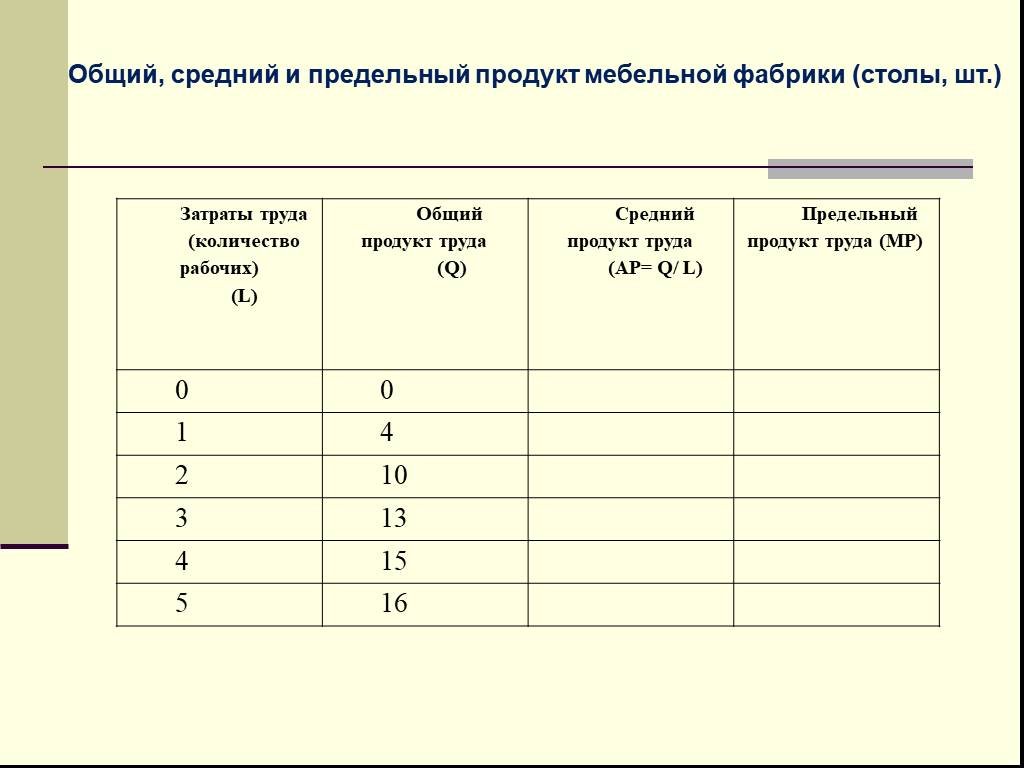
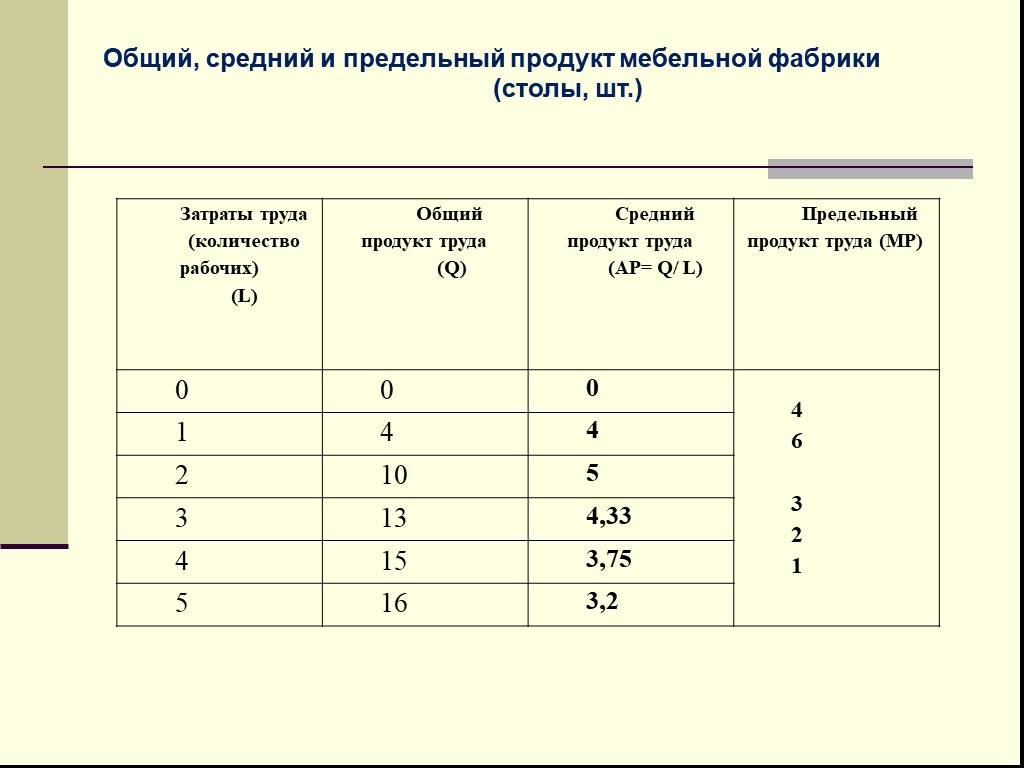
Презентация "Экономический смысл производной" по математике – проект, доклад

Интегрированный урок математики и экономики по теме :

«Экономический смысл производной»

ИМЯ УРОКА

«Успех порождает успех!»

Девиз дня: «Если мы действительно что-то знаем, то мы знаем это благодаря изучению математики» (Пьер Гассенди). «Рано или поздно всякая правильная математическая идея находит применение в том или ином деле» (А. Н. Крылов).

Тип урока: урок обобщения, повторения и систематизации знаний Цели: обобщить, систематизировать, углубить полученные знания по теме « Производная» и показать практическое применение в экономике.

Задачи: Образовательные: Расширить представления по изученной теме. Показать связь между математикой и экономикой. Раскрыть роль производной в исследовании процессов производства. Закрепить знания, умения и навыки в применении правил вычисления производной к решению практических задач с экономическим содержанием. Развивающие: Раскрыть практическую и теоретическую значимость темы «Производная ». Развивать логическое мышление при установлении связи экономических величин с понятием производной. Развивать навыки групповой работы. Воспитательные: Формировать понятие о научной организации производства.

Этапы урока: Повторение темы «Правила вычисления производных». Повторение темы «Производительность труда». Разработка алгоритма решения задач на конкретном примере. Решение задач в группах по карточкам. Практическая работа по применению производной в заданиях при подготовке к ЕГЭ (ФИПИ) Подведение итогов урока.

Экономика – это наука об ограниченности и выборе, а также можно определить как общественную науку, которая описывает и анализирует выбор общества при ограниченных ресурсах для удовлетворения потребностей. Экономику сегодня нужно представлять, как совокупность методов, создающих условия для выживания и прогресса человечества. Многие экономические понятия, такие как депозит, акция, стоимость, инфляция, прибыль, банковский процент, банкротство, дивиденды, производительность труда составляют тот фон, на котором проходит жизнь нашего общества. Поэтому, сегодня встает вопрос об экономической грамотности общества, его культуре.

В процессе обучения, вы убедились в том, что различные науки не могут существовать изолировано, например, для успешного изучения физики, необходимо хорошо владеть вычислительными навыками. Нельзя заниматься биологией не зная химии. Но есть одна наука, без которой невозможна никакая другая. Это математика. Ее понятия, представления и символы служат тем языком, на котором говорят, пишут и думают другие науки. При помощи математического аппарата возможно моделирование практической деятельности в реальной жизни, ее отдельных сторон, качеств и областей. На сегодняшнем уроке мы и попытаемся установить связь между экономикой и математикой. Поэтому урок мы будем вести вдвоем.

1.Устная работа. Рассмотрим основные характеристики дифференциального исчисления. А)Какая математическая величина обозначается данной буквой?: Δх; Δу; f(g(x)); у’ ; с’ ; f(g(x))’. Б) Самостоятельная работа на знание формул и правил дифференцирования. В) Презентация устного счёта по нахождению производной и её практического применения.

2. Блицопрос (теоретический): Что называется дифференцированием функции? Геометрический смысл производной? Физический смысл производной? Что называется производной функции в т. Х0?

Что изучает экономика? Что называется экономией? Производительность труда? Что такое объем продукции?

Общий продукт (Q) – это объем продукции, произведенный фирмой за определенный период времени (например, за год).

Поскольку объем производства зависит от объема использованных ресурсов, то зависимость между ними может быть выражена в виде следующей функциональной записи: Q = f(L,K), где Q - максимальный объем продукции, произведенной при данной технологии и определенных факторах производства; L - труд; К - капитал; f - функция.

Средний продукт (производительность, эффективность труда) – выпуск продукции в расчете на единицу труда (одного работника; один человеко-час труда). АП=Q/L Предельный продукт труда (МР) – это прирост общего продукта в результате применения дополнительной единицы труда (дополнительной рабочей силы).

Общий, средний и предельный продукт мебельной фабрики (столы, шт.)

Производительность труда — мера (измеритель) эффективности труда. Производительность труда измеряется количеством продукции, выпущенной работником за какое-то время. Из определения следует, что производительность труда определяется объемом выпущенной продукции в течение определенного времени. В экономике очень часто объем произведенной продукции задается формулой. Например, пусть объем продукции выпущенной в течение дня задан формулой у = -2t³ +10t² +50t – 16, где t – время, выраженное в часах. Для нахождения производительности труда в определенный промежуток времени t0, необходимо найти предельное среднее значение средней производительности за период времени от t0 до t0 + Δt, т.е. у´(х).

ВЫВОД: производительность труда есть производная объема выпускаемой продукции.

Задача: Вычислить производительность труда во время каждого часа работы, при условии, что объем продукции у в течение рабочего дня представлен функцией у = -2t³ +10t² +50t – 16, t– время (ч).

Решение: 1. Найдем производную у´(t) = -6t² +20t + 50 2. Найдем значение производной в течение каждого часа, t=1 y’(1) = -6*1² +20*1 + 50= 64 t=2 y’(2) = -6*2² +20*2 + 50= 66 t=3 y’(3) = -6*3² +20*3 + 50= 56 t=4 y’(4) = -6*4² +20*4 + 50= 34 t=5 y’(5) = -6*5² +20*5 + 50= 0

После второго часа работы производительность работы начинает падать. Такой результат является следствием усталости, ухудшением условий в помещении и много других факторов, влияющих на производительность труда. Обратите ваше внимание, на то, что недостаточно просто найти результат, главное правильно сделать выводы.

Задания для групп: Вычислить производительность труда во время первых 4 часов работы, если объем продукции у в течение рабочего дня представлен функцией и сделать выводы. 1 группа: у = -t³ +10t² +40t – 16, t– время, ч. 2 группа: у = -2t² +10t+50, t– время, ч. 3 группа: у = -3t³ +20t² +100t – 6, t– время, ч. 4 группа: y = -0,5t³ + 20t² + 30t -4? t-время,ч..

Подведение итогов. Оценивание. Как вы видите, важно не только получить ответ, но и соотнести его с реальностью. Зная теорию, теперь вы готовы к тому, чтобы решать и другие проблемы, возникающие на предприятии.

Домашнее задание: Повторить алгоритм исследования функции с помощью производной. Повторить тему издержки производства. Прототип задания B8 (№ 119975),с. 26, ФИПИ.(решить 3 задачи)