Презентация "Задания с производной при подготовке к ЕГЭ Задания В8 и В14" по математике – проект, доклад
Презентацию на тему "Задания с производной при подготовке к ЕГЭ Задания В8 и В14" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 28 слайд(ов).
Слайды презентации
Список похожих презентаций
«Решение задания С1 ЕГЭ по информатике и ИКТ»
2 балла. Решение задания С1 ЕГЭ по информатике и ИКТ. Кунина В.В. область I область II. 0 x y y = x+2 y2 + x2 = 25 y2 + x2 25 y 0 x 0 область ...«Применение производной для исследования функции»
Справимся легко! №1. По графику функции y=f(x) ответьте на вопросы: Сколько точек максимума имеет эта функция? Назовите точки минимума функции. Сколько ...Автоматизация труда учителя на примере решения систем алгебраических уравнений с использованием программного пакета MATHCAD
Ознакомить учителей математики с возможностями продукта MathCAD Обеспечить автоматизацию работы учителей с использованием MathCAD Рассмотреть решение ..."Комбинаторика и вероятность"
Диктант ******- это раздел математики, посвященный задачам выбора и расположения предметов из различных множеств. Произведение натуральных чисел от ..."Турнир веселых и смекалистых знатоков истории, физики, химии, математики"
Цели мероприятия: 1.Развитие у учащихся интереса к изучаемым предметам. 2.Показать необходимость знаний по математике в других науках. 3.Формирование ...«Закрепление изученого» (Сложение и вычитание с переходом через десяток в пределах 20)
Цели урока:. 1. Закрепить знания о сложении и вычитании с переходом через десяток в приделах 20. 2. Упражняться в решении задач изученных видов. План ...Авторские задачи по математике и физике, составленные по повести Н.В. Гоголя «Ночь перед Рождеством
Методологическая основа: Класс арифметических задач огромен. Учащиеся старших классов обычно пытаются решать такие задачи алгебраически, так как владеют ..."Целые числа и действия с ними". 6-й класс
«Сумма двух долгов есть долг». «Сумма имущества и долга равна их разности». (– 3) + (– 5) = – 8 4 + (– 7) = 4 – 7 = – 3. – 8 · (– 2) = 4; – 9 : (– ..."Функция y = kx², ее свойства и график". 8-й класс
Траектория движения комет в межпланетном пространстве. Архитектурные сооружения. . Траектория движения. Тема урока. Функция у=кх2, ее график и свойства ...Cинус, косинус, тангенс и котангенс угла
Тест. Синус угла А равен: а) 4/5; б) 3/5; в) 4/3 2.Тангенс угла В равен: а) 4/3; б) 3/5; в)¾ 3.Косинус. равен : а) б) ½; в). 4. Упростить выражение:. ..."Все действия с обыкновенными дробями"
Великие открытия ученых математиков ХХ века. «Математика является значительно большим, чем наука, поскольку она является языком науки». Нильс Бор, ...«Математический бой. Через тернии к звездам»
. Разминка. Сколько разных букв в названии нашей страны? 5 букв. ДВЕНАДЦАТЬ. К семи прибавить пять. Как правильно записать: одиннадцать или адиннадцать? ...«Параллельность прямых и плоскостей»
ABCD – трапеция, AD , E и F – середины AB и CD соответственно. Докажите, что EF ǁ α. α. α. α. α. A B C D α. Через вершины А и С параллелограмма ABCD ...I Функция У=АХ², её график и свойства
А=1 У=Х ². А=2 У=2Х ². У=Х² У=2Х². Растяжение от оси Х в два раза. А=0.5 У=Х² У=0.5Х². Сжатие по оси Х в два раза. Вообще график функции У=АХ² можно ...«Действия с обыкновенными дробями (2)»
Урок по теме «Действия с обыкновенными дробями». На острове Дробей. 1. Сократите дроби. 2. Исключите целую часть из числа. 3. Переведите число в неправильную ...«Табличное умножение и деление» Устный счёт
Решите задачу: Во раз б 9 шт. 3 шт.. 9:3=3 (раза)- во столько раз апельсинов больше, чем яблок. 7∙5=35 (яб.). У резной избушки На лесной опушке Бельчата ...«Сложение положительных и отрицательных чисел».
. Кемеровская область. Если в картину Сибири всмотреться, На ней обозначены контуры сердца. И бьется оно. И отчизна внимает Рабочему ритму Кузнецкого ...«Сложение и вычитание десятичных дробей»
Чтобы сложить (вычесть) десятичные дроби, нужно: 1) уравнять в этих дробях количество знаков после запятой; 2) записать их друг под другом так, чтобы ...«Решение задач с помощью пропорций»
Найти значение Х: Х:3=4:6 5:Х=2:6 7:3=Х:18 Устная работа. Указать вид пропорциональной зависимости:. Какова зависимость пути от времени? Какова зависимость ..."Сложение и вычитание рациональных чисел"
I. II. III. IV. Тема: "Сложение и вычитание положительных и отрицательных чисел". Станции: Историческая Биологическая Географическая Математическая. ...Конспекты
Алгебра и начала анализа 10 класс
Алгебра и начала анализа 10 класс(поурочные планы). . 1-е полугодие. . Глава 1. Числовые функции. . Уроки 1-2. Определение числовой функции ...Арифметические действия с целыми числами
Ваш выбор: «Курить или долго жить.». Урок по математике в 6 кл коррекционной школы. Тип урока. . Обобщение и закрепление знаний по теме : ...Веселая и полезная математика
. Тюрина Валентина Викторовна. 1 квалификационная категория – учитель математики. Город Прокопьевск Кемеровская область. МКОУ «Школа – интернат ...Вероятность и математическая статистика
Открытый урок. . по учебной дисциплине Теория вероятностей и математическая статистика. Тема: «Вероятность и математическая статистика». Группа ...Арифметический квадратный корень и его свойства
Урок - повторение по теме: «Арифметический квадратный корень и его свойства». . . Учитель Переверзева М.В. МБОУСОШ «11. . Цель: подвести итоги ...Арифметические действия с положительными и отрицательными числами
. Муниципальное бюджетное общеобразовательное учреждение«Лицей №2». Методическая разработка урокаматематики. «Арифметические действия ...Арифметические действия с числами
Методическая разработка урокаматематики. «Арифметические действия с. числами. ». для учащихся 6-го класса. Аннотация. Повторение изученного ...Арифметические действия с дробями
. Муниципальное бюджетное общеобразовательное учреждение«Лицей №2». Урокматематики для 5 класса. «Арифметические действия с дробями». ...Арифметические действия с дробями
. Муниципальное бюджетное общеобразовательное учреждение«Лицей №2». Методическая разработка урокаматематики. «Арифметические действия ...Арифметическая и геометрическая прогрессии
ПЛАН-КОНСПЕКТ УРОКА Арифметическая и геометрическая прогрессии. . ФИО (полностью). . Науменкова Олеся Анатольевна. . . . Место ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:25 апреля 2015
Категория:Математика
Содержит:28 слайд(ов)
Поделись с друзьями:
Скачать презентацию









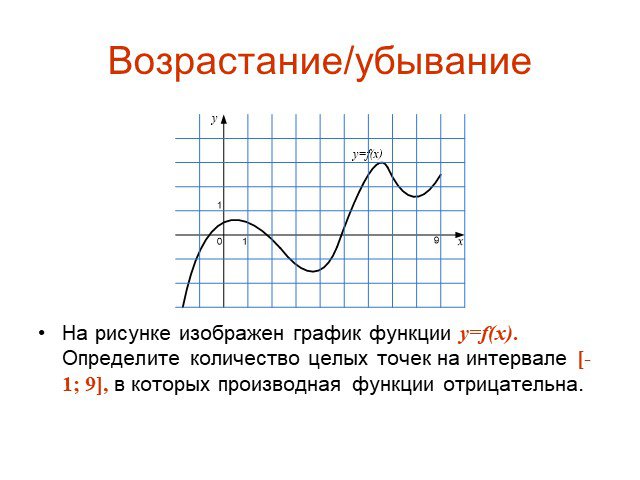

















![Возрастание/убывание. На рисунке изображен график функции y=f(x). Определите количество целых точек на интервале [-1; 9], в которых производная функции отрицательна. Возрастание/убывание. На рисунке изображен график функции y=f(x). Определите количество целых точек на интервале [-1; 9], в которых производная функции отрицательна.](https://prezentacii.org/upload/cloud/15/04/41018/images/thumbs/screen14.jpg)
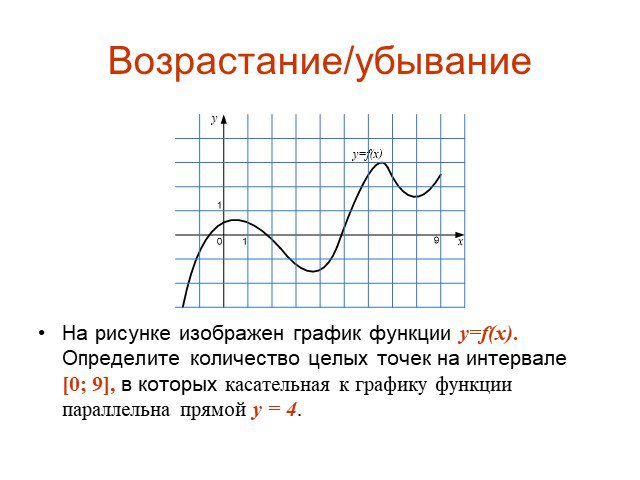
![На рисунке изображен график функции y=f(x). Определите количество целых точек на интервале [0; 9], в которых касательная к графику функции параллельна прямой y = 4. На рисунке изображен график функции y=f(x). Определите количество целых точек на интервале [0; 9], в которых касательная к графику функции параллельна прямой y = 4.](https://prezentacii.org/upload/cloud/15/04/41018/images/thumbs/screen15.jpg)
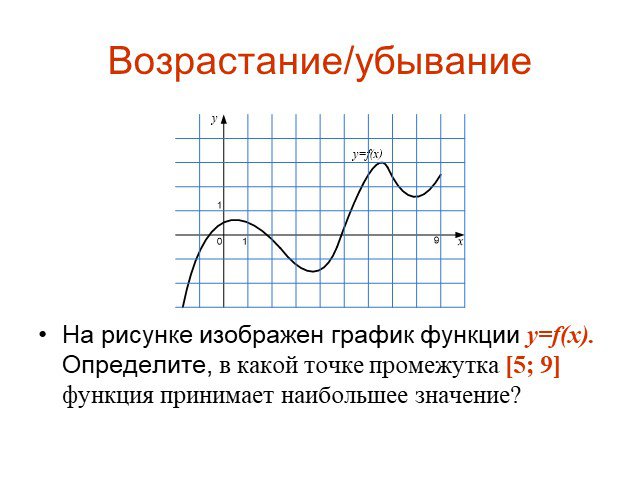
![На рисунке изображен график функции y=f(x). Определите, в какой точке промежутка [5; 9] функция принимает наибольшее значение? На рисунке изображен график функции y=f(x). Определите, в какой точке промежутка [5; 9] функция принимает наибольшее значение?](https://prezentacii.org/upload/cloud/15/04/41018/images/thumbs/screen16.jpg)
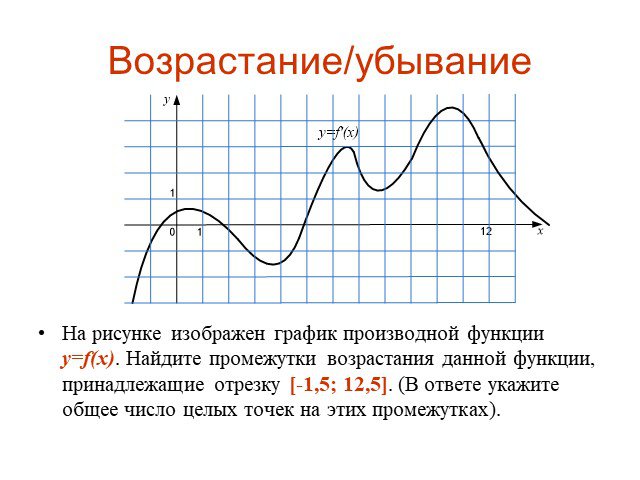
![На рисунке изображен график производной функции y=f(x). Найдите промежутки возрастания данной функции, принадлежащие отрезку [-1,5; 12,5]. (В ответе укажите общее число целых точек на этих промежутках). На рисунке изображен график производной функции y=f(x). Найдите промежутки возрастания данной функции, принадлежащие отрезку [-1,5; 12,5]. (В ответе укажите общее число целых точек на этих промежутках).](https://prezentacii.org/upload/cloud/15/04/41018/images/thumbs/screen17.jpg)
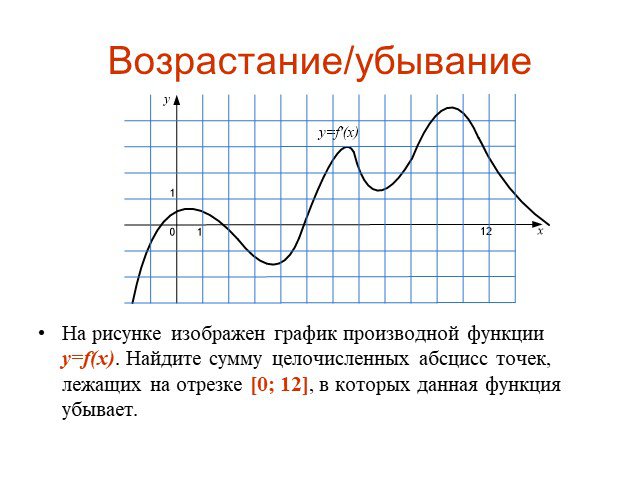
![На рисунке изображен график производной функции y=f(x). Найдите сумму целочисленных абсцисс точек, лежащих на отрезке [0; 12], в которых данная функция убывает. На рисунке изображен график производной функции y=f(x). Найдите сумму целочисленных абсцисс точек, лежащих на отрезке [0; 12], в которых данная функция убывает.](https://prezentacii.org/upload/cloud/15/04/41018/images/thumbs/screen18.jpg)


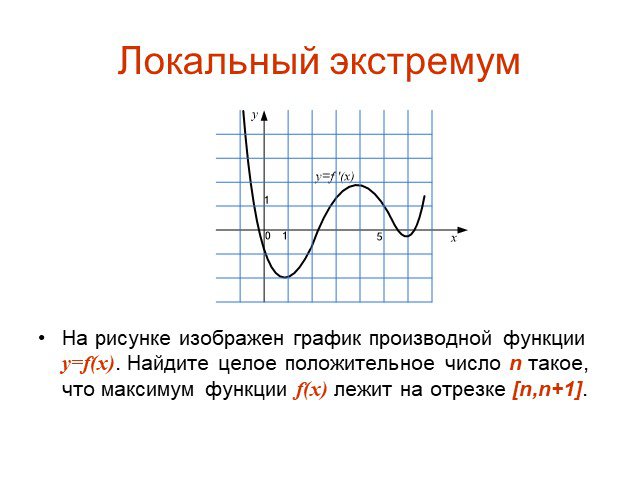
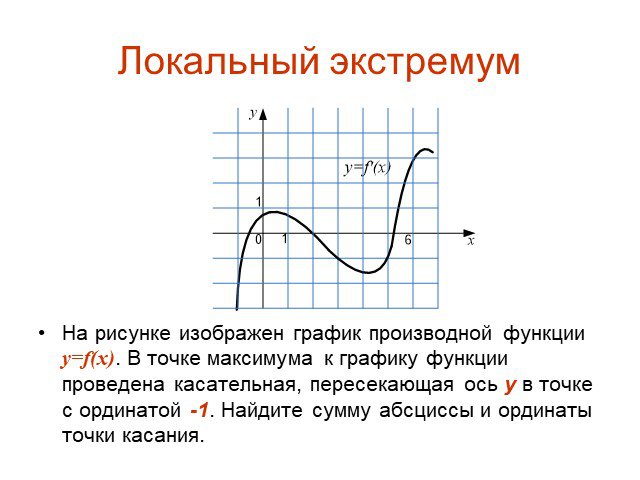
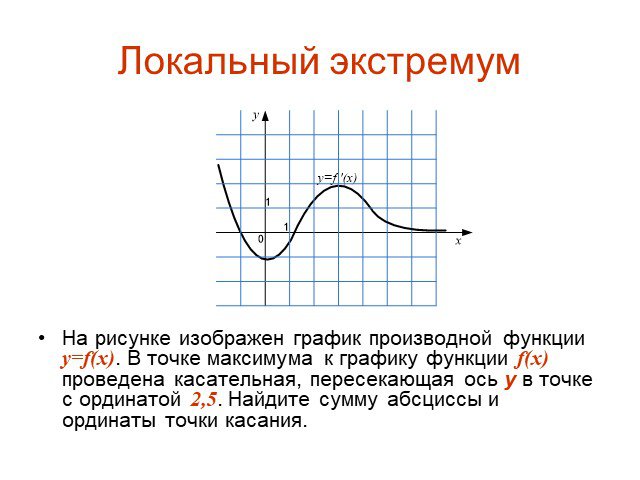
![Локальный экстремум. На рисунке изображен график производной функции y=f(x). Найдите целое положительное число n такое, что максимум функции f(x) лежит на отрезке [n,n+1]. Локальный экстремум. На рисунке изображен график производной функции y=f(x). Найдите целое положительное число n такое, что максимум функции f(x) лежит на отрезке [n,n+1].](https://prezentacii.org/upload/cloud/15/04/41018/images/thumbs/screen21.jpg)


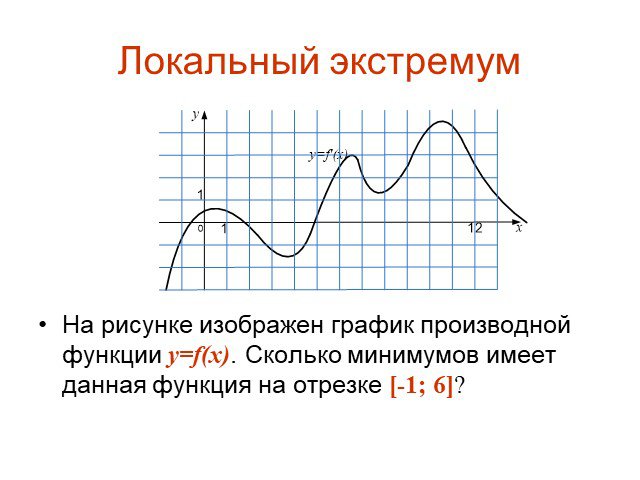
![На рисунке изображен график производной функции y=f(x). Сколько минимумов имеет данная функция на отрезке [-1; 6]? На рисунке изображен график производной функции y=f(x). Сколько минимумов имеет данная функция на отрезке [-1; 6]?](https://prezentacii.org/upload/cloud/15/04/41018/images/thumbs/screen24.jpg)


![Найдите точку, в которой функция y=2x3 + 9x2 – 60x +1 принимает наибольшее значение на промежутке [-6; 6]. Найдите значение функции y=1/4x4 - 2x2 +5 в точке максимума Найдите наименьшее значение функции y=π/√3 - √3 x – 2 cosx + 11 на отрезке [0; π/2] Найдите точку, в которой функция y=2x3 + 9x2 – 60x +1 принимает наибольшее значение на промежутке [-6; 6]. Найдите значение функции y=1/4x4 - 2x2 +5 в точке максимума Найдите наименьшее значение функции y=π/√3 - √3 x – 2 cosx + 11 на отрезке [0; π/2]](https://prezentacii.org/upload/cloud/15/04/41018/images/thumbs/screen27.jpg)
![Найдите количество целых значений а, при которых функция y= -x3/3 + (a+2)x2 – 4x +10 не имеет точек экстремума. Найдите количество целых значений функции y= х + 16/(х-1) на отрезке [-4; 0] Найдите наименьшее значение функции y=22x + 2x+1 – xln16 + 3 на отрезке [-1;2] Найдите наименьшее значение функ Найдите количество целых значений а, при которых функция y= -x3/3 + (a+2)x2 – 4x +10 не имеет точек экстремума. Найдите количество целых значений функции y= х + 16/(х-1) на отрезке [-4; 0] Найдите наименьшее значение функции y=22x + 2x+1 – xln16 + 3 на отрезке [-1;2] Найдите наименьшее значение функ](https://prezentacii.org/upload/cloud/15/04/41018/images/thumbs/screen28.jpg)