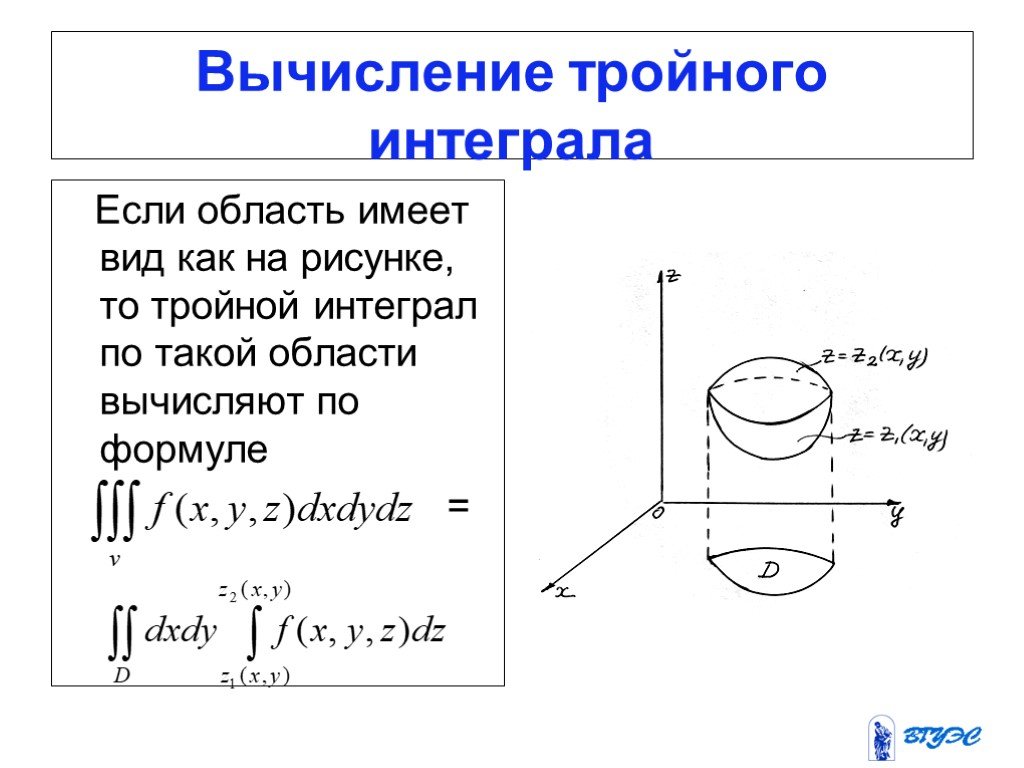
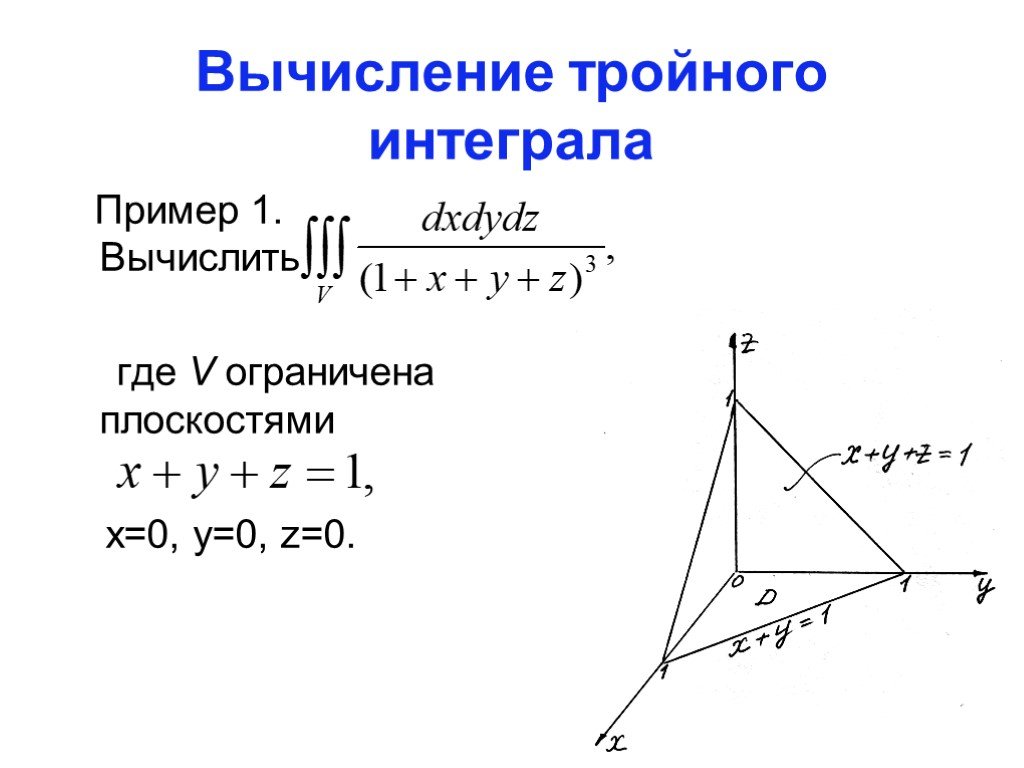
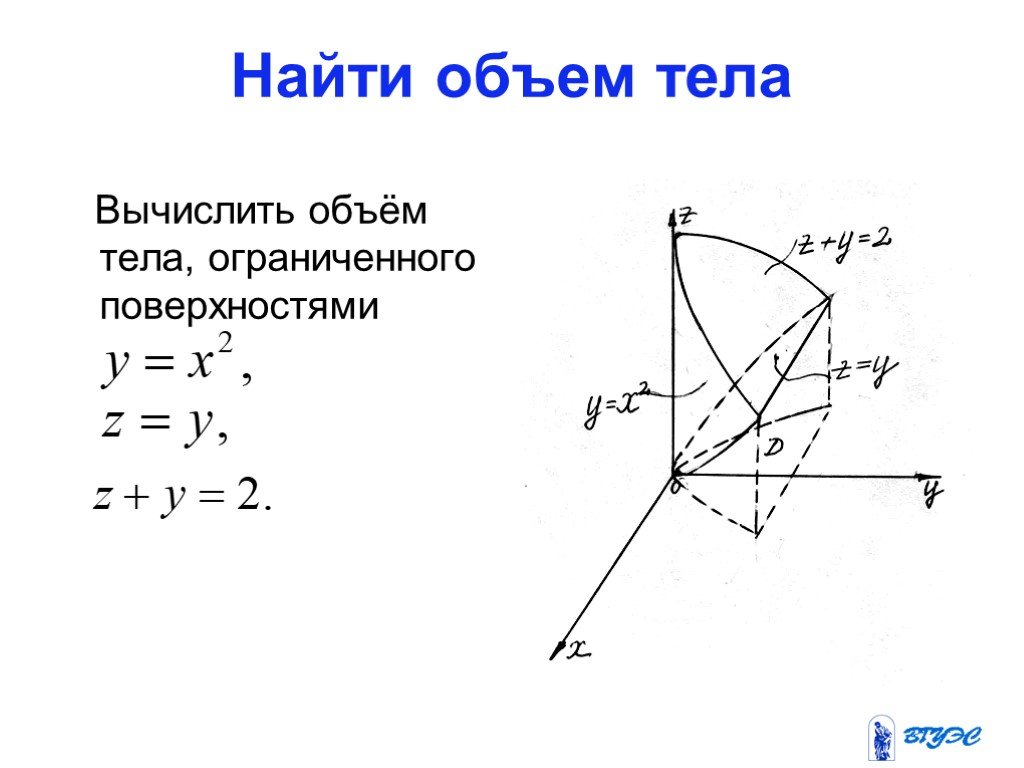
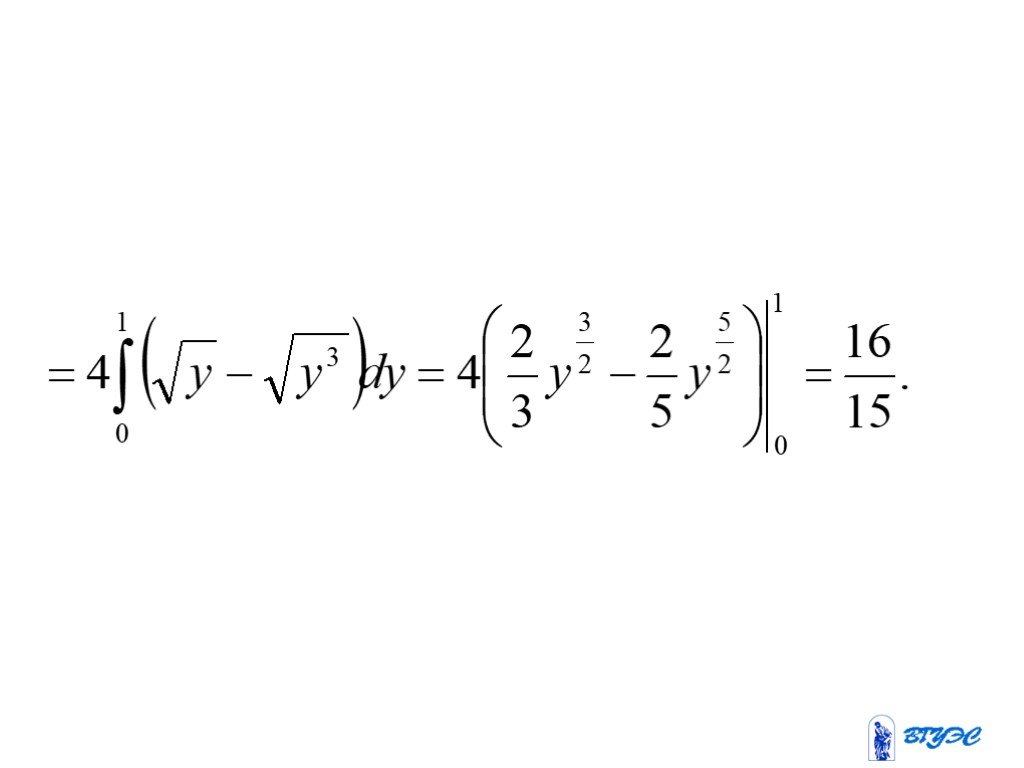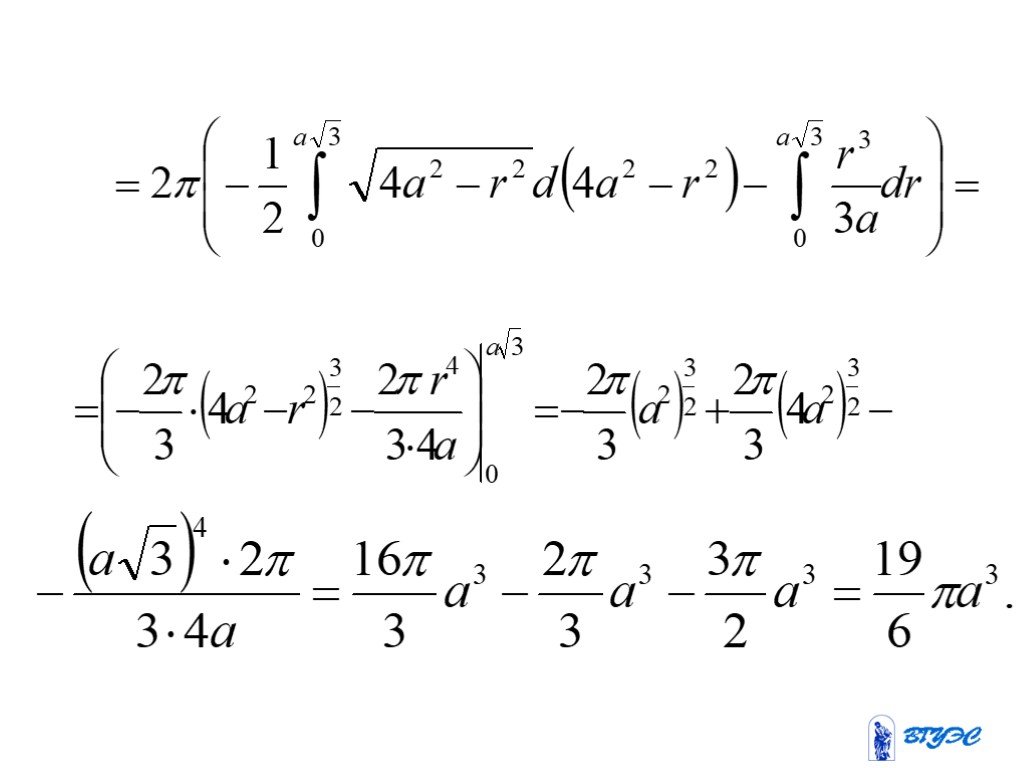Презентация "Тройной интеграл" по математике – проект, доклад
Презентацию на тему "Тройной интеграл" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 21 слайд(ов).
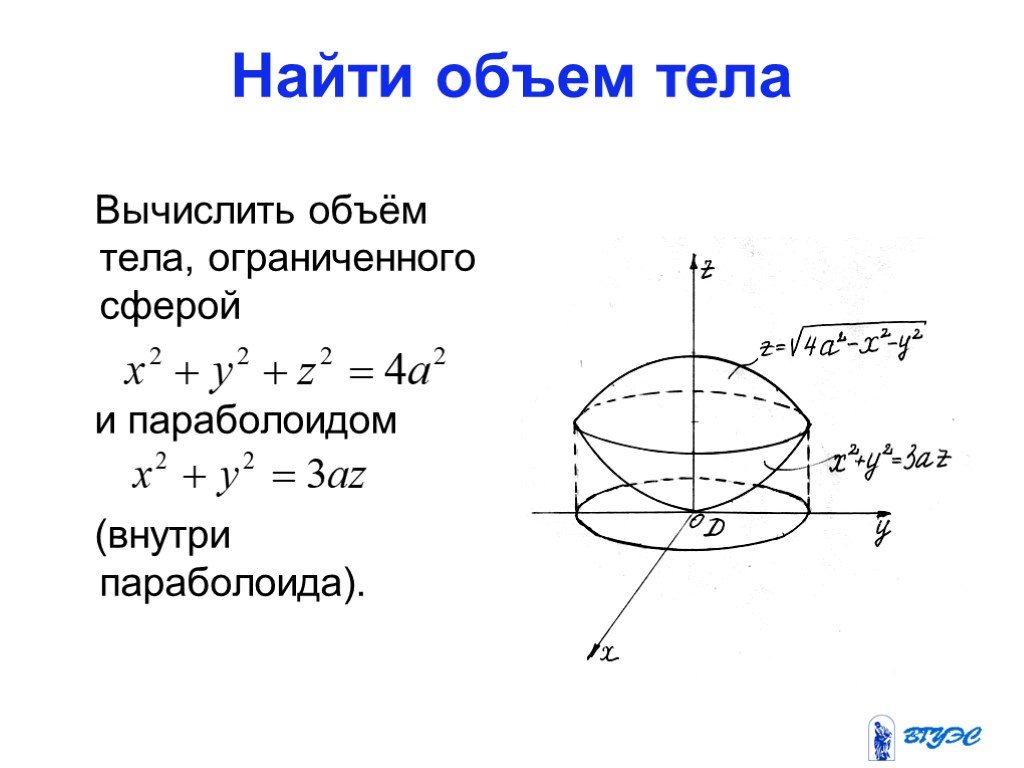
Слайды презентации
Список похожих презентаций
Площадь криволинейной трапеции и интеграл
Криволинейная трапеция. Отрезок [a;b] называют основанием этой криволинейной трапеции. Криволинейной трапецией называется фигура, ограниченная графиком ...Неопределенный интеграл
Элементы интегрального исчисления. 1.Первообразная и неопределенный интеграл 2.Основные приемы вычисления неопределенных интегралов 3.Интегрирование ...Первообразная и интеграл
Исторические сведения. Интегральное исчисление возникло из потребности создать общий метод Разыскания площадей , объемов и центров тяжести. В зародышевой ...Первообразная и неопределенный интеграл
По заданным производным найдите исходные функции. дифференцирование. интегрирование. Обозначения: ПЕРВООБРАЗНАЯ. Функция F называется первообразной ...Определенный интеграл и его применение
План. 1. Понятие определённого интеграла 2. Пример 3. Свойства определённого интеграла 4. Определённый интеграл с переменным верхним пределом 5. Применение ...Определенный интеграл
y=f(x) a b y x. Формула Ньютона-Лейбница. «Разобъем» трапецию таким образом, что…. В пределе имеем …. Как найти площадь трапеции …? A, B, N S: = 0 ...Неопределённый интеграл и его свойства
План. Неопределённый интегра́л; Подведение под знак дифференциала; Основные методы интегрирования; Таблица основных неопределённых интегралов; Примеры ...Дифференциал и интеграл
Функция. Предел функции. Функцией называется соответствие при котором каждому значению x из некоторого множества D (DR) сопоставляется по некоторому ...Задания по впр математика
№1. Найди значение примера: 43 − 27 Найди значение выражения: 7 + 3⋅(8 +12) ОТВЕТЫ 16 67. № 2. Рассмотри рисунок и ответь на вопрос: сколько рублей ...ЕГЭ математика готовимся к С4
Прямая, перпендикулярная гипотенузе, отсекает от него четырёхугольник, в который можно вписать окружность. Найдите радиус окружности, если отрезок ...Конкурс "Ох, уж эта математика"
Зал красочно оформлен: на стенах математические газеты. Рисунки, кроссворды, высказывания ученых. Их портреты. В жюри трое родителей. Ведущая Счетный ...Занимательная математика для детей (устный счёт + учимся писать цифры)
По дороге мальчик и девочка шли, Оба по два рубля нашли. За ними ещё трое идут. Сколько они денег найдут? Повезло опять Егорке, У реки сидит не зря. ...Занимательная математика
Профессор ложится спать в 8 часов вечера и заводит будильник на 9 часов утра. Сколько часов будет спать профессор? Профессор. Рядом с берегом со спущенной ...Занимательная математика
РАЗМИНКА Миша тратит на дорогу в школу 5 минут. Сколько минут он потратит на эту дорогу вдвоём с мамой? Какие сто букв могут остановить движение транспорта? ...Занимательная математика
Интеллектуальная игра. Играем. Во сколько раз должны некие объекты превосходить остальные, чтобы по праву называться гигантскими? В миллиард раз (гига). ...Занимательная математика
Проблема проекта:. многим ученикам не интересно заниматься математикой. Они считают её сухой и незанимательной наукой, поэтому у них плохие отметки ..."Электрики и математика"
Воспитательные Воспитание умения работать в команде, уважения к сопернику, воспитание чувства ответственности; Воспитание чувства ответственности, ...Занимательная математика
Подводная арифметика. Детёныш голубого кита выпивает за день 600 л молока. Сколько молока выпьет такой малыш за месяц (30 дней)? Ответ: 18 000 л. ...«Координатная плоскость» математика
Цели и задачи урока:. 1. Ввести понятие координатной плоскости, уметь определять координаты точек, строить точки по их координатам. 2. Развивать мышление, ...Занимательная математика в младших классах
Круглый, румяный. В печке печён, На окошке стужён. Кто я? Колобок. Проверка 5, 8, 4, 6, 7, 0, 1, 2 Молодцы! Задача. Семь снегирей на ветке сидели. ...Конспекты
Первообразная и интеграл
Автор: Макарова Татьяна Павловна, учитель математики ГБОУ СОШ №618 г. Москвы. . Тест. Первообразная и интеграл. Автор:. . . Макарова Татьяна ...Первообразная и интеграл
Муниципальное общеобразовательное учреждение. . «Средняя общеобразовательная школа №3 г. Козьмодемьянска». . Республики Марий Эл. . ...Определенный интеграл
Автор:. Лушина Татьяна Владимировна. Полное название образовательного учреждения. : Муниципальное общеобразовательное учреждение лицей (г.Орехово-Зуево ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:28 мая 2019
Категория:Математика
Содержит:21 слайд(ов)
Поделись с друзьями:
Скачать презентацию