Презентация "Применение свойств тригонометрических функций" по математике – проект, доклад
Презентацию на тему "Применение свойств тригонометрических функций" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 15 слайд(ов).
Слайды презентации
Список похожих презентаций
Общие свойства функций
Вариант 1 Вариант 2 Задача 1. Найти область определения функции. Задача 2. Функция f(x) возрастающая. Сравните f(3) и f(5). Функция f(x) убывающая. ...Основные свойства функций
Определение. Числовой функцией с областью определения D называется соответствие, при котором каждому числу х из множества D сопоставляется по некоторому ...Преобразование графиков тригонометрических функций
Цели урока:. Обобщить и систематизировать знания учащихся по теме. Показать актуальность темы в связи с введением ЕГЭ в штатный режим. Показать возможности ...Нахождение значений тригонометрических функций с помощью таблиц Брадиса
Четырёхзначные таблицы В.М. Брадиса. Владимир Модестович Брадис - математик, педагог. Родился 23 декабря 1890 года в семье учителей начальной школы ...Преобразование графиков тригонометрических функций
Параллельный перенос на вектор (0; b) вдоль оси ординат: График функции f(x)+b получается параллельным переносом графика f(x) в положительном направлении ...Преобразование графиков тригонометрических функций
y = cos(x+2) y=cos2x y=sinx +2 y=-3cosx y=sin1/2x y=sin(x-5) y=tg2x y=2ctgx y=ctg1/3x y=1/3sinx y=4-cosx y=ctgx+1. Сгруппируйте функции по какому-нибудь ...Построение графиков тригонометрических функций
формирование знаний и умений преобразовать графики тригонометрических функций. Цель:. Закрепить применение программы MS Excel для построения графиков ...Преобразование графиков тригонометрических функций
Цель урока:. Повторить свойства тригонометрических функций Изучить графическую программу Advanced Grapher, облегчающую построение графиков Изучить ...Исследование тригонометрических функций
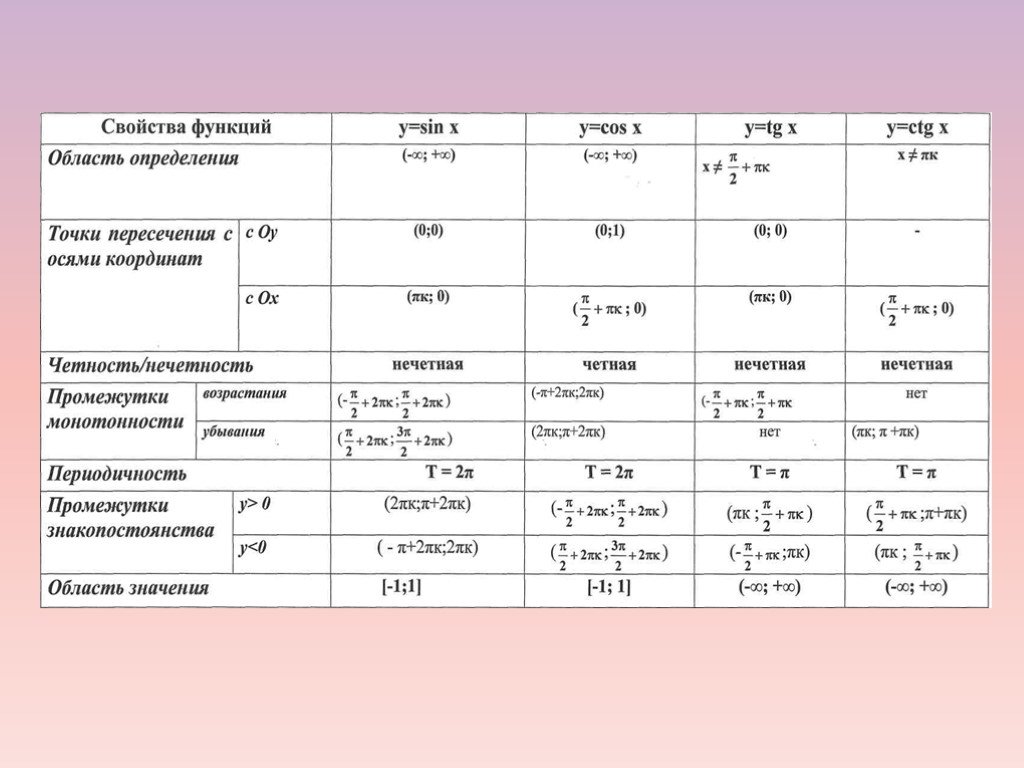
Содержание. Область определения функции Область значения функции Периодичность Промежутки знакопостоянства Четность и нечетность функций Возрастание ...Применение неравенств и их свойств
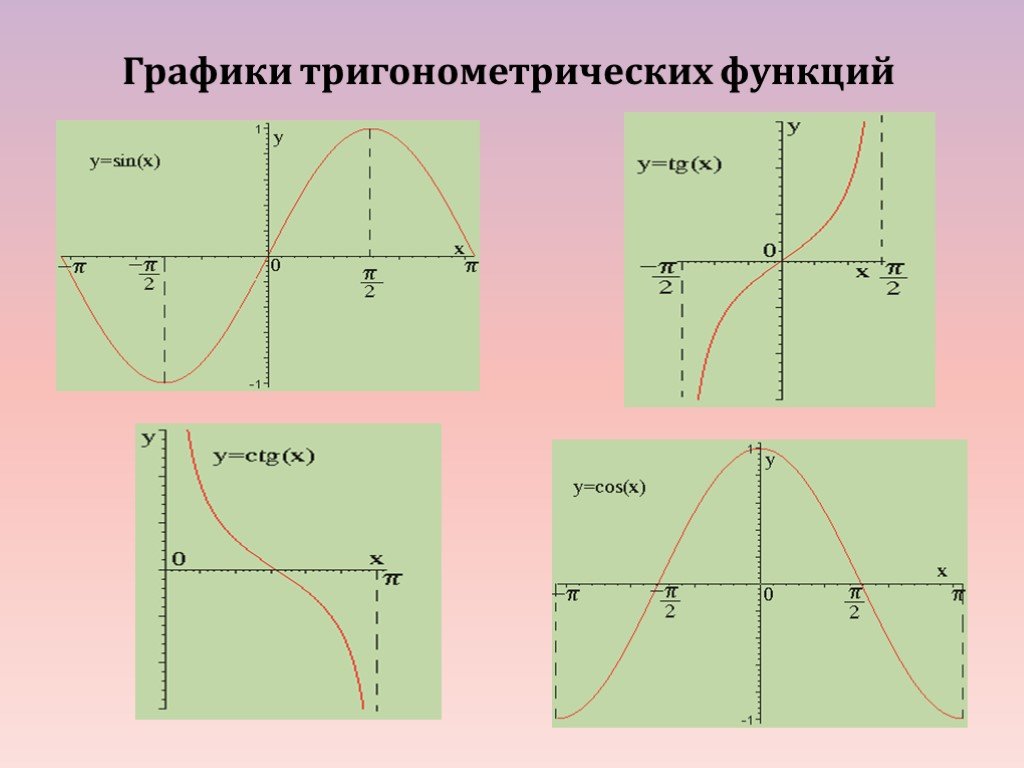
научиться применять теорию о числовых неравенствах при решении смешанных задач. развивать умение применять свойства числовых неравенств в нестандартной ...Графики тригонометрических функций
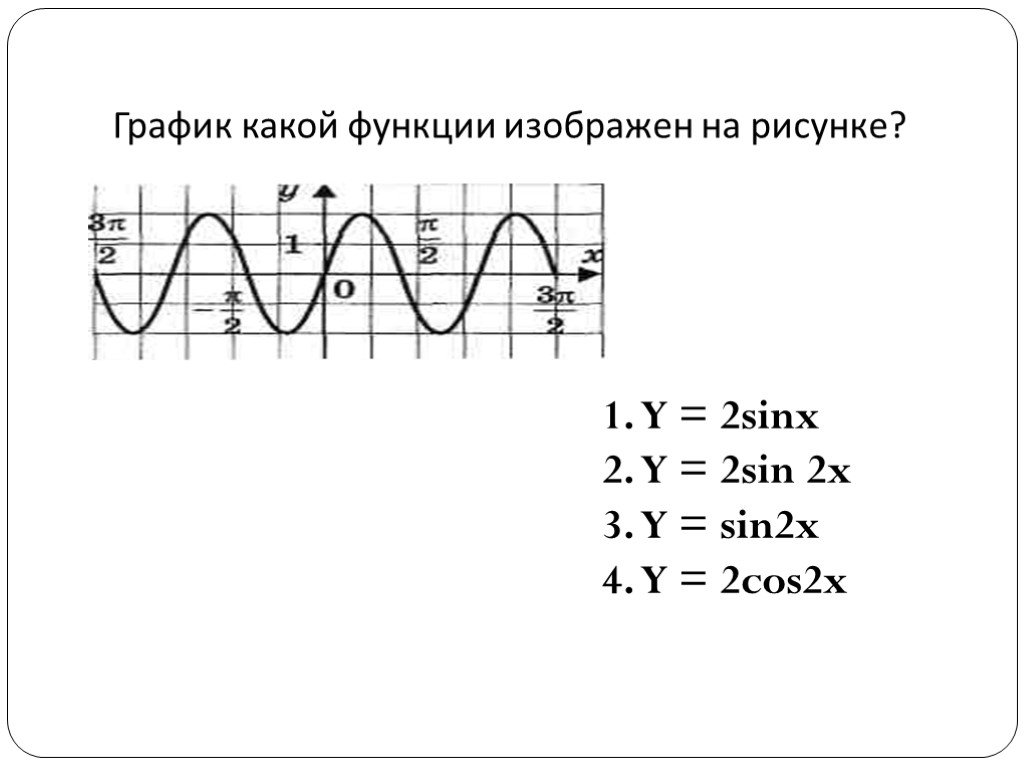
тригонометрические функции. Графиком функции у = sin x является синусоида. Свойства функции: D(y) =R Периодическая (Т=2p) Нечетная (sin(-x)=-sin x) ...Преобразование графиков тригонометрических функций
Оборудование урока: компьютер, проектор, экран. Цели: Обобщить знания и умения. Развить умение наблюдать, сравнить, обобщать. Воспитать познавательную ...Дополнения к значениям тригонометрических функций
Цели и задачи работы:. Нахождение способов вычисления значений тригонометрических функций нестандартных углов; Изучение литературы о тригонометрии ...Применение векторов к решению задач
Цели: Показать применение векторов при решении геометрических задач на конкретных примерах; Совершенствовать навыки выполнения действий над векторами. ...Преобразование функций
Задачи урока. Повторить правила преобразований:. Построить преобразования тригонометрических функций:. Изучить гармоническую функцию:. Преобразование: ...Преобразование графиков функций на координатной плоскости
Эпиграф к уроку. Красота в единстве теории и практики. Цели обучения, воспитания и развития. Рациональные способы построения графиков функций. Развитие ...Построение диаграмм и графиков функций
Диаграмма (график) — это наглядное графическое представление числовых данных. Основные типы диаграмм. Линейчатая Круговая Линии (график). показывает ...Построение графиков функций, содержащих выражения под знаком модуля
Цель работы:.построение графиков графики функций, содержащие выражения под знаком модуля. Частный случай (под знаком модуля одно выражение и нет ...
Алгебра функций
Конспект занятия. Учитель Винник Надежда Анатольевна Предмет: Элективный курс по математике «Алгебра функций» Тип занятия: занятие-практикум Тема ...Графики функций с модулями
Цель работы:. Научится строить графики функций с модулями. Хорошая подготовка к ЕГЭ. 1 ФУНКЦИЯ С МОДУЛЕМ. Y=lXl Строим график функции у = x Из-за ...Конспекты
Применение свойства монотонности функций при решении уравнений и неравенств
Тамбовское областное государственное автономное образовательное учреждение – общеобразовательная школа – интернат. . «Мичуринский лицей». ...Применение свойств рациональных чисел для рационализации вычислений
Тема: Применение свойств рациональных чисел для рационализации вычислений. Тип урока:. Формирование умений и навыков. Цели урока:. Обучающие:. ...Производные функций и применение производной
Государственное бюджетное общеобразовательное учреждение. . средняя общеобразовательная школа с. Чёрный Ключ. . муниципального района Клявлинский ...Применение свойств квадратного корня
План- конспект урока. Применение свойств квадратного корня. (Тема урока). . ФИО (полностью):. . Старикова Валентина Валерьевна. . ...Применение тригонометрических формул к преобразованию выражений
МБОУ гимназия №4. г.Озёры Московская область. Урок по теме:. 10 класс. Учитель математики Хлыстова Т.В. Конспект урока по алгебре ...Применение свойств квадратных корней
Урок по алгебре в 8 классе. Учитель:. Патрина Татьяна Николаевна, МОУ СОШ №120 с углубленным изучением отдельных предметов Московского района города ...Применение свойств арифметического квадратного корня
Урок математики по теме: "Применение свойств арифметического квадратного корня" (8-й класс). . Аксютченко. . Жанна Владимировна,. учитель математики. ...Применение свойств арифметического квадратного корня
ПЛАН-КОНСПЕКТ УРОКА «Применение свойств арифметического квадратного корня». . ФИО (полностью). . . Рыжова Наталья Михайловна. . ...Применение распределительного свойства умножения
Муниципальное бюджетное общеобразовательное учреждение. «Средняя общеобразовательная школа пос. Молодёжный». Альметьевский муниципальный район. ...Применение распределительного свойства умножения
«Применение распределительного свойства умножения». Цели. : закрепить умения в использовании распределительного свойства умножения при решении примеров, ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:3 апреля 2019
Категория:Математика
Содержит:15 слайд(ов)
Поделись с друзьями:
Скачать презентацию









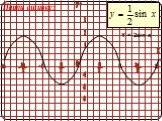
![Укажите множество значений функции. Y = sin 3x + 2 1. [-2; 2] 2. [-1; 5] 3. [1; 3] 4. [-3; 3] Укажите множество значений функции. Y = sin 3x + 2 1. [-2; 2] 2. [-1; 5] 3. [1; 3] 4. [-3; 3]](https://prezentacii.org/upload/cloud/19/04/138994/images/thumbs/screen9.jpg)
![Y = COS2 4x – 4 1. [-4; 4] 2.[-5; -3] 3. [1; 4] 4. [-4 ; -3] Y = COS2 4x – 4 1. [-4; 4] 2.[-5; -3] 3. [1; 4] 4. [-4 ; -3]](https://prezentacii.org/upload/cloud/19/04/138994/images/thumbs/screen10.jpg)
![Y = tg x + 2 1. [0; +∞] 2. (-∞; +∞) 3. [2; +∞] 4. (2; +∞) Y = tg x + 2 1. [0; +∞] 2. (-∞; +∞) 3. [2; +∞] 4. (2; +∞)](https://prezentacii.org/upload/cloud/19/04/138994/images/thumbs/screen11.jpg)
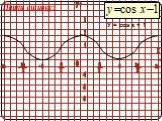
![Укажите функцию, множеством значений которой является промежуток. [-3; 1] 1. Y = COS X – 1 2. Y = 2 SIN X - 1 3. Y = -2SIN X – 1 4. Y = 3 COS X Укажите функцию, множеством значений которой является промежуток. [-3; 1] 1. Y = COS X – 1 2. Y = 2 SIN X - 1 3. Y = -2SIN X – 1 4. Y = 3 COS X](https://prezentacii.org/upload/cloud/19/04/138994/images/thumbs/screen12.jpg)

![ПРОВЕРЬ СЕБЯ! 1. [-4; 4] 2. [1; 3] 3. 5 4. Y = - SIN X + 1 ПРОВЕРЬ СЕБЯ! 1. [-4; 4] 2. [1; 3] 3. 5 4. Y = - SIN X + 1](https://prezentacii.org/upload/cloud/19/04/138994/images/thumbs/screen15.jpg)






























