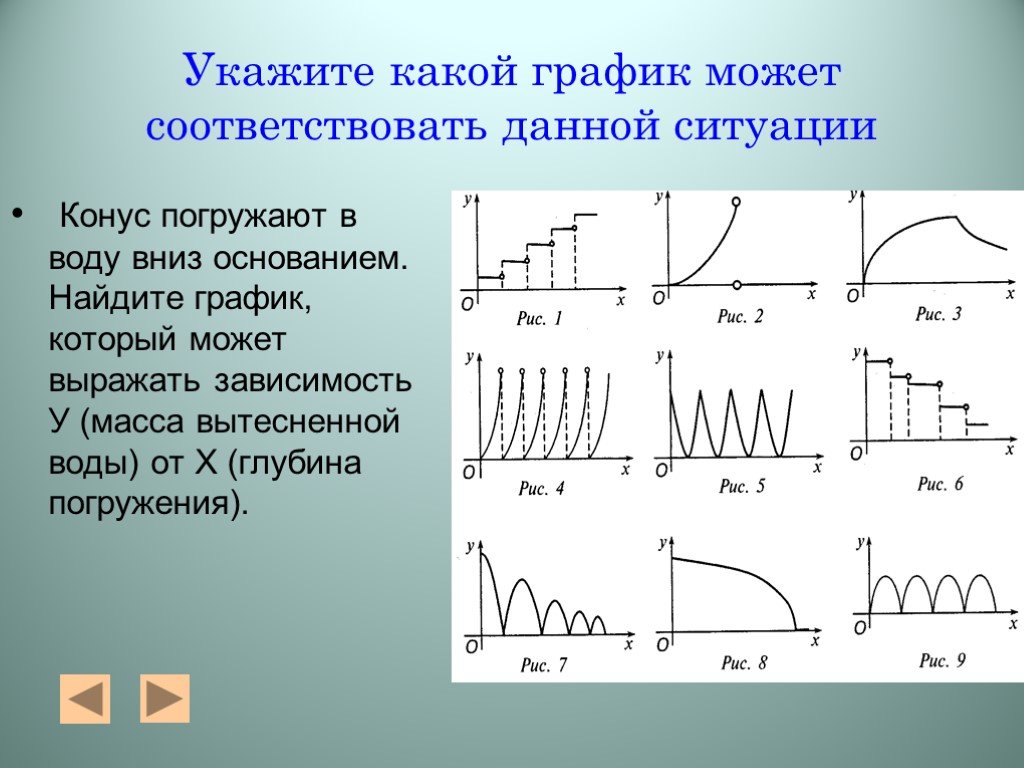
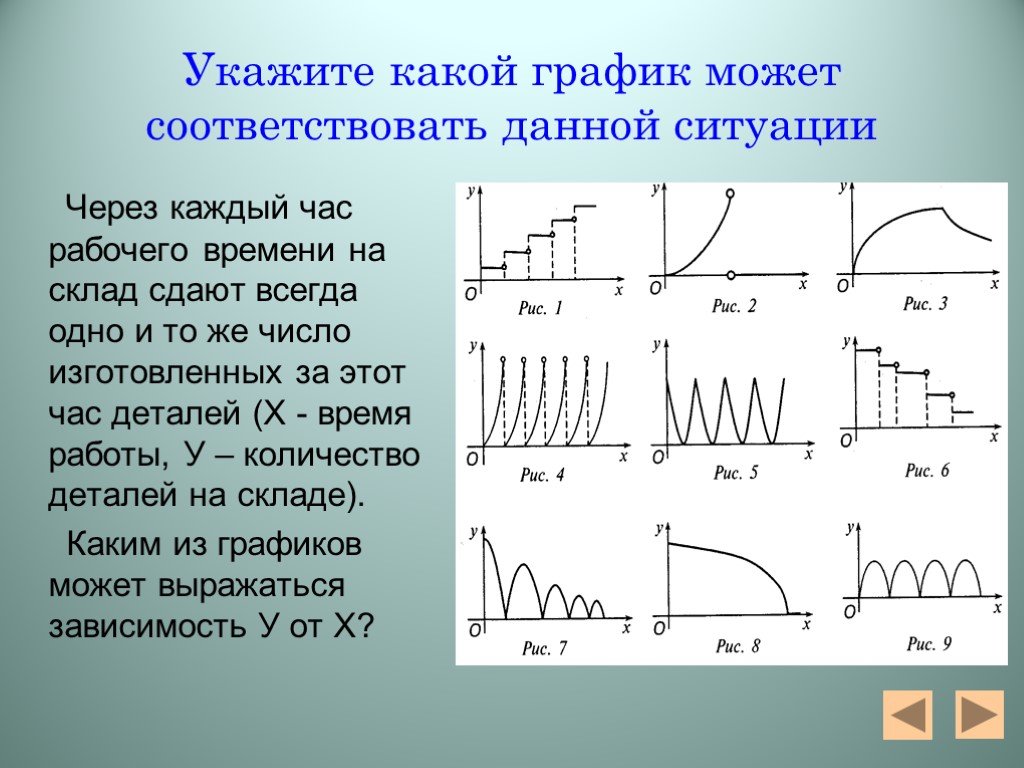
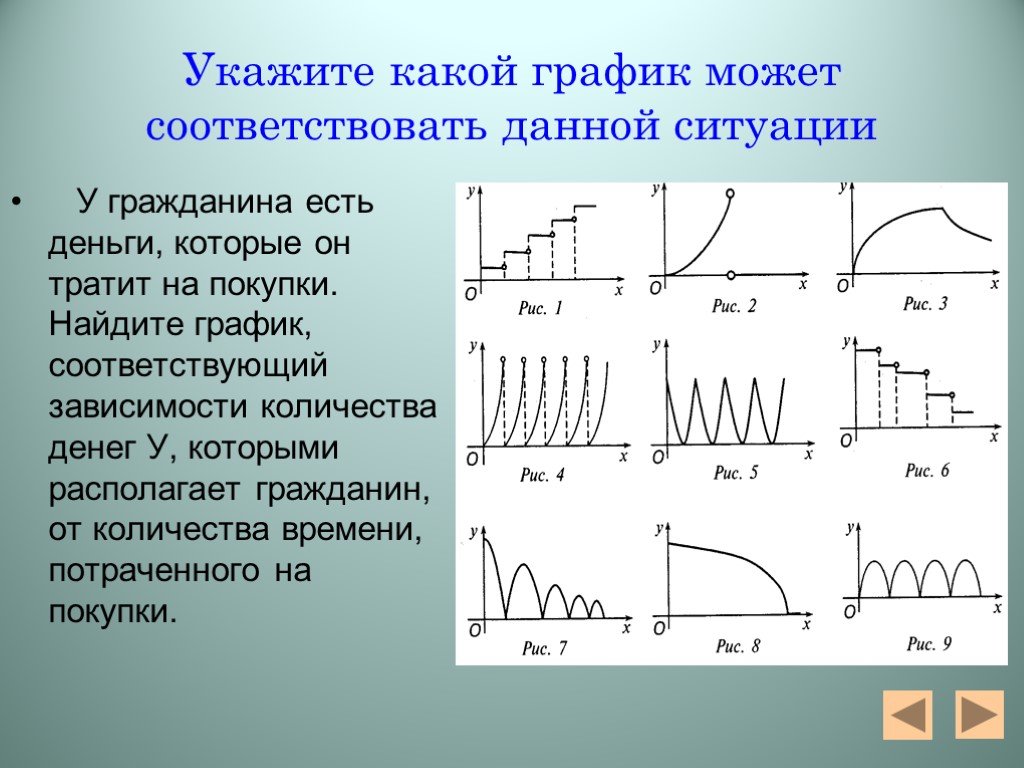
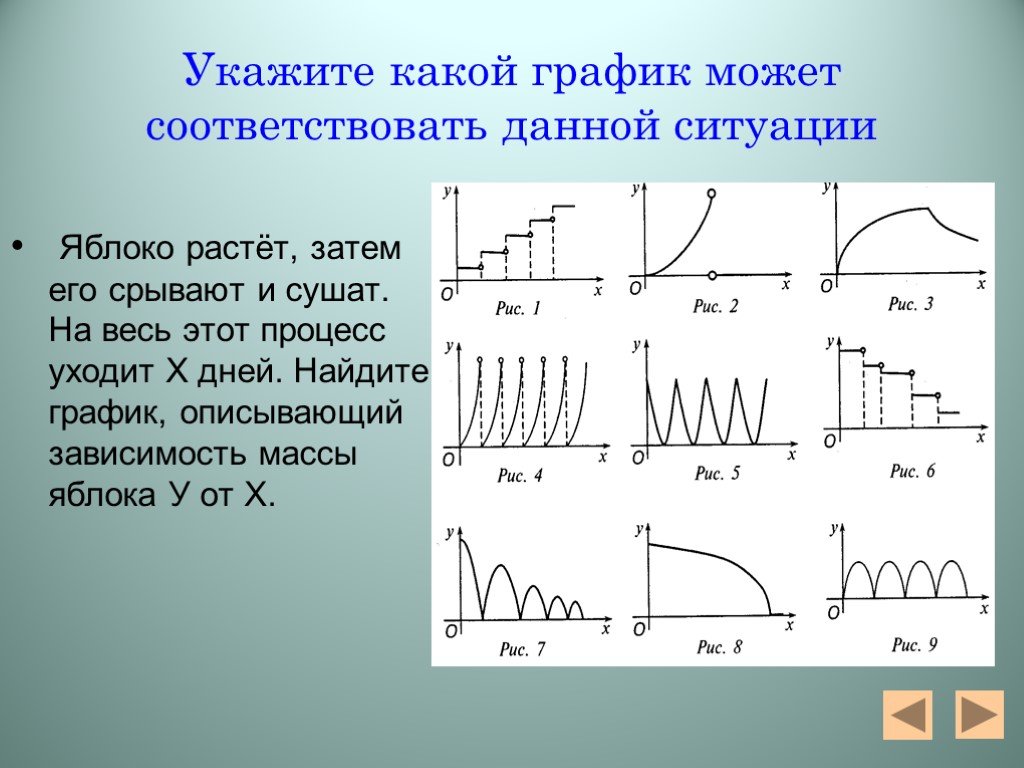
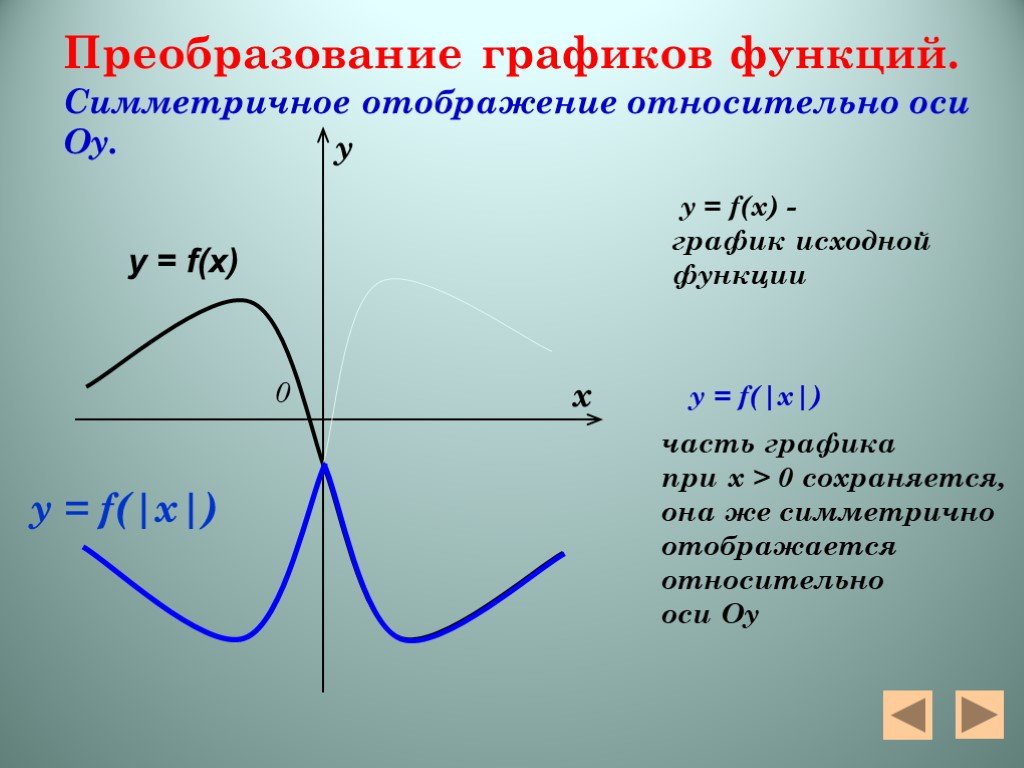
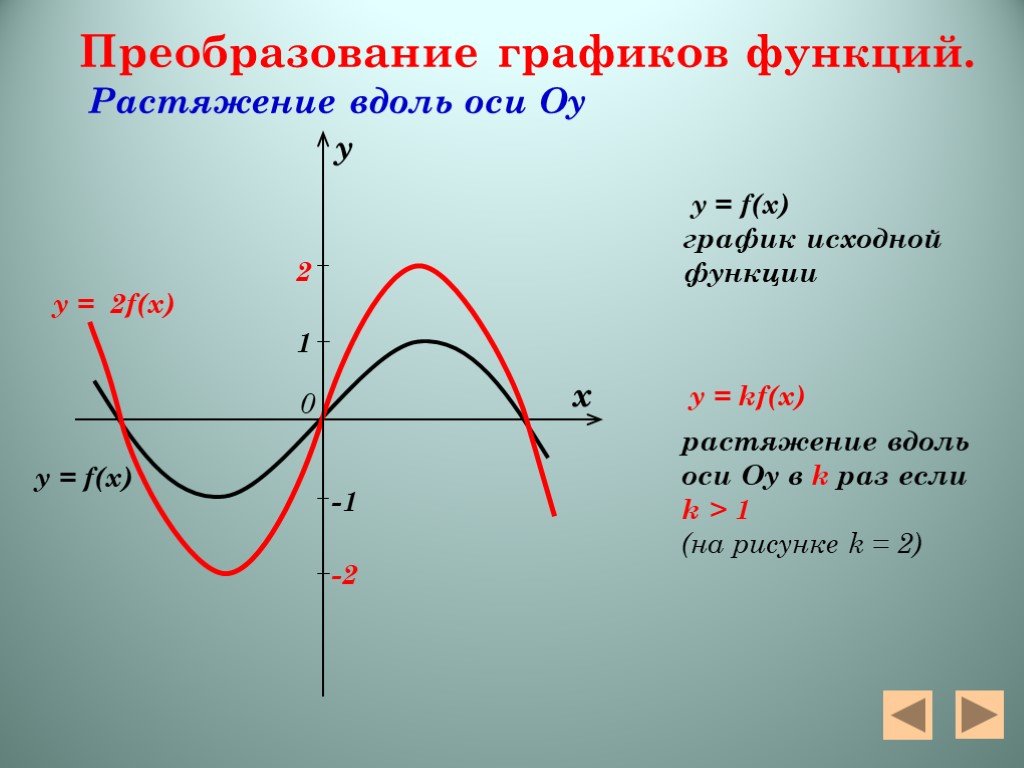
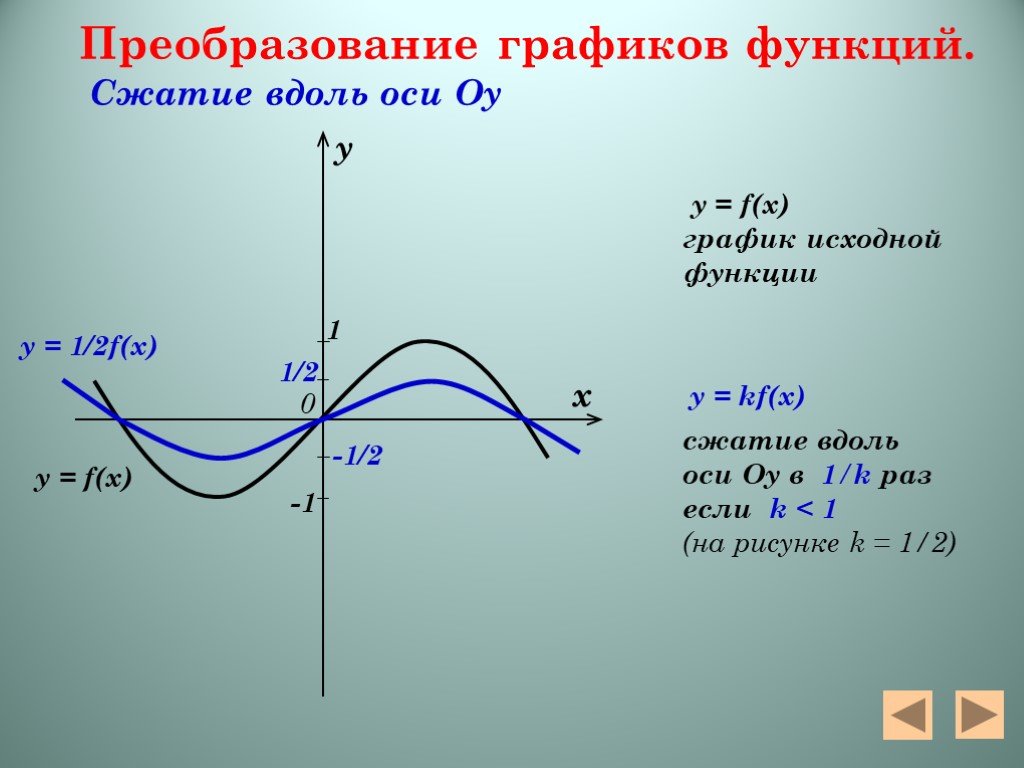
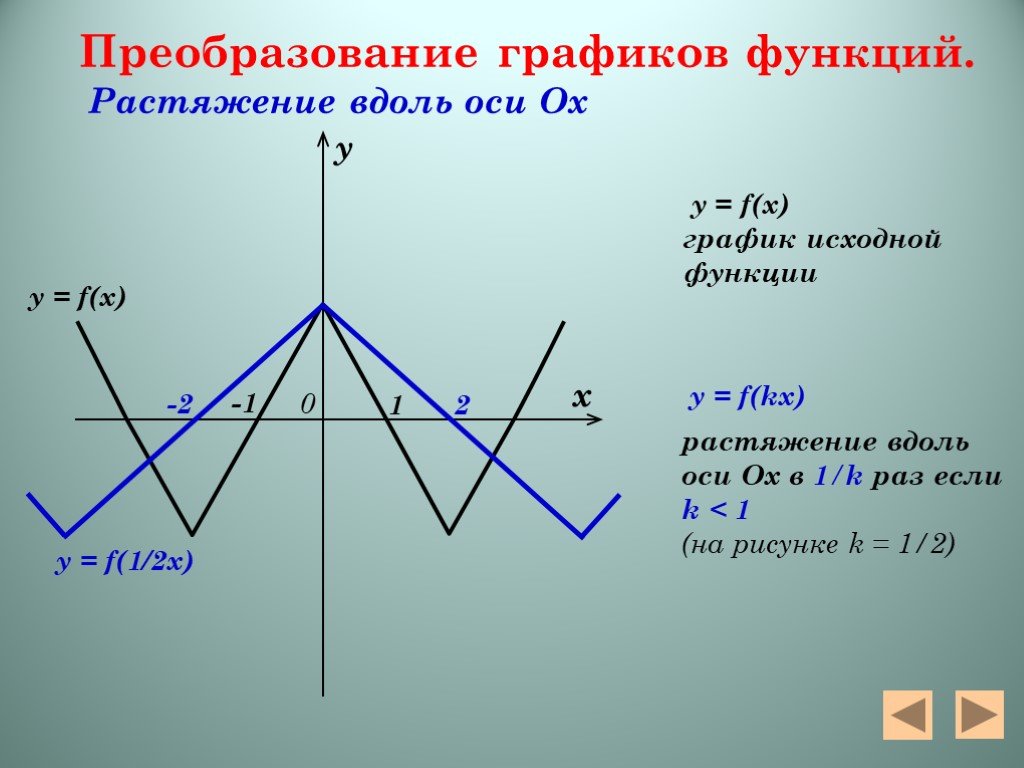
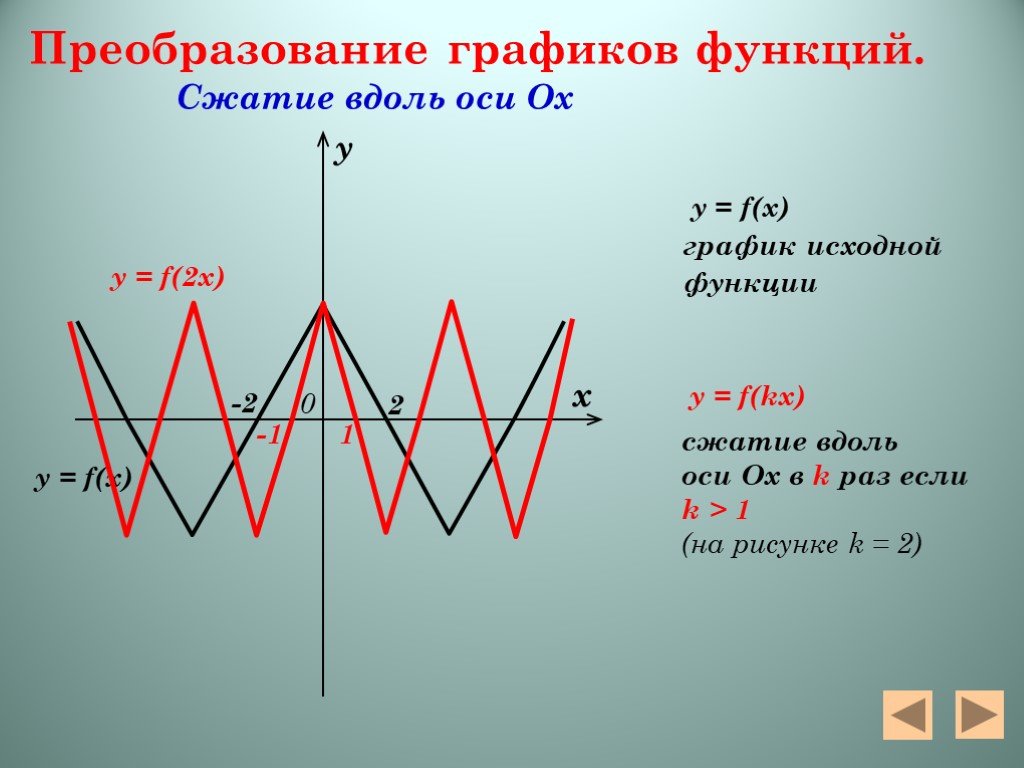
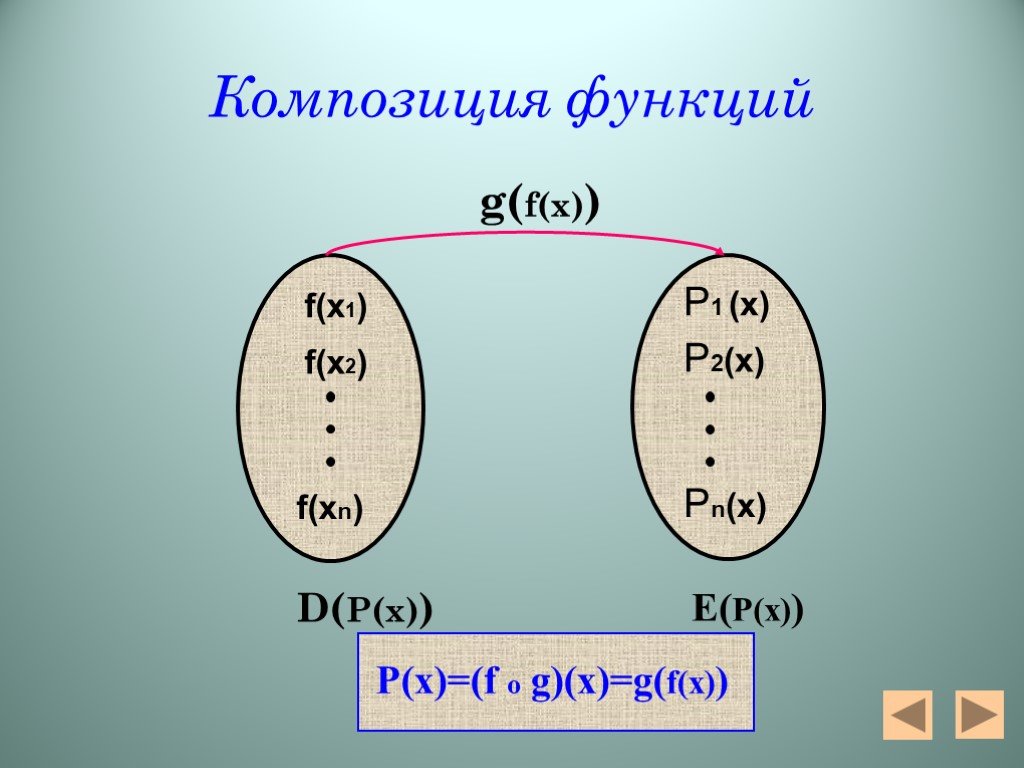
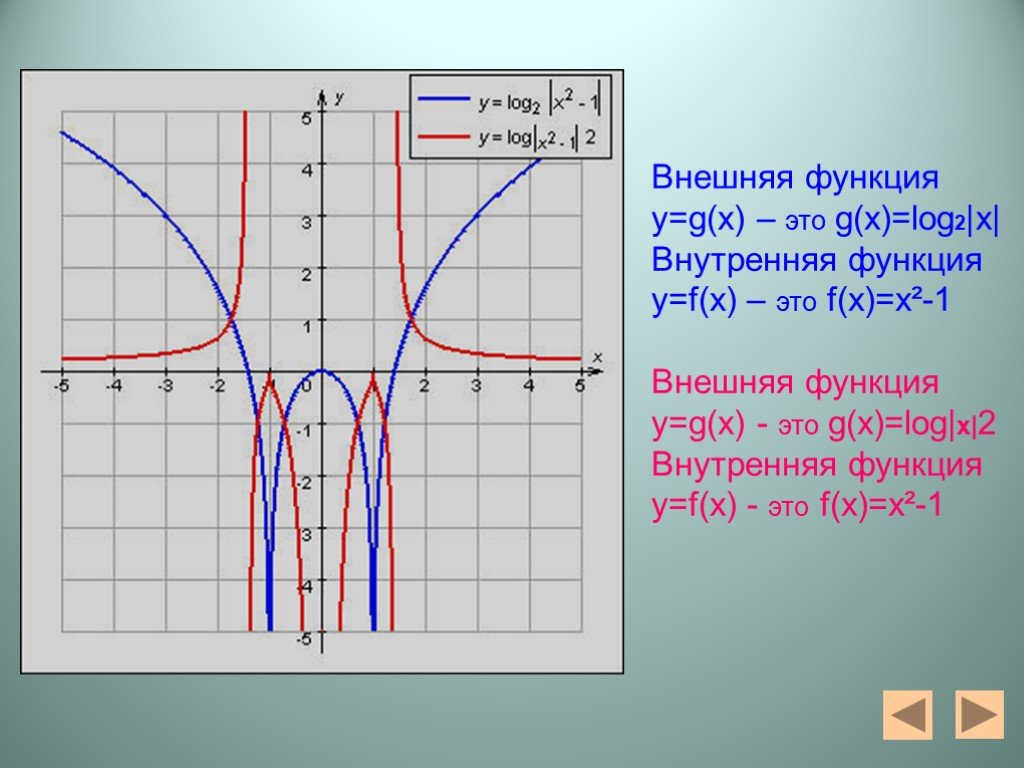
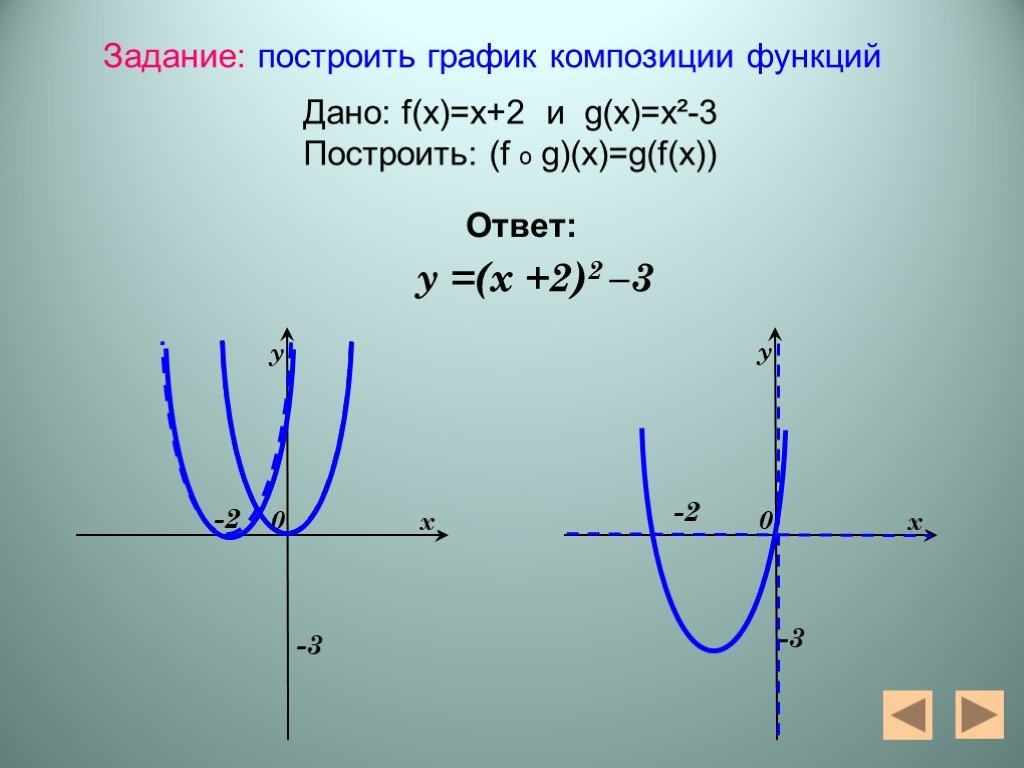
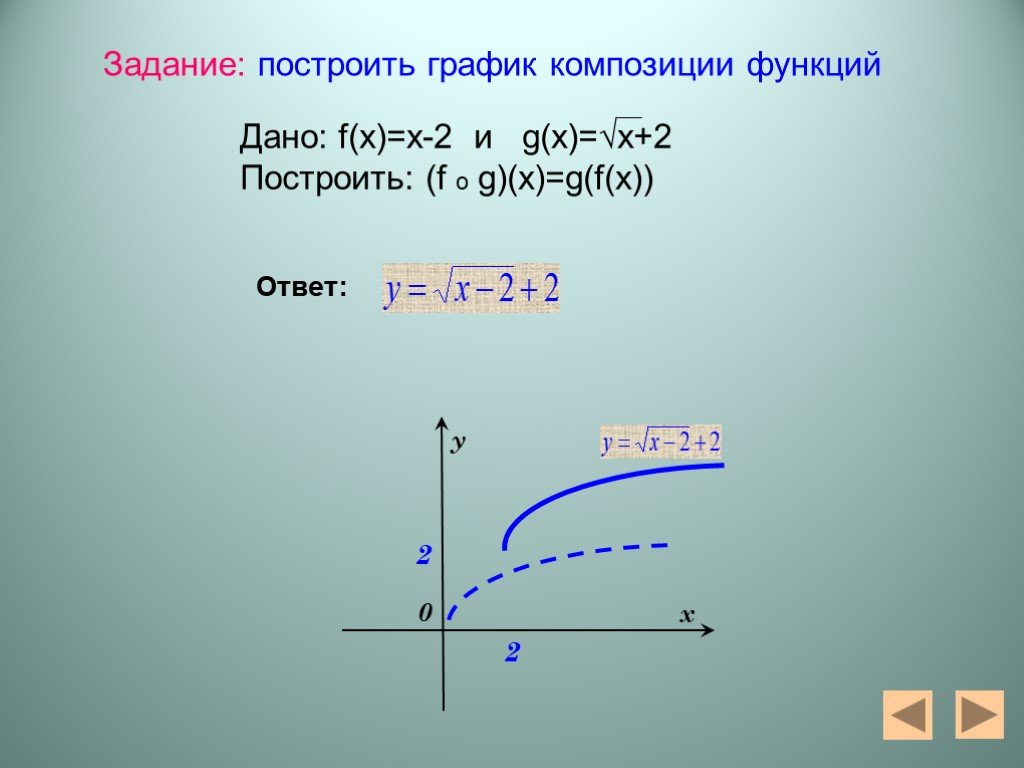
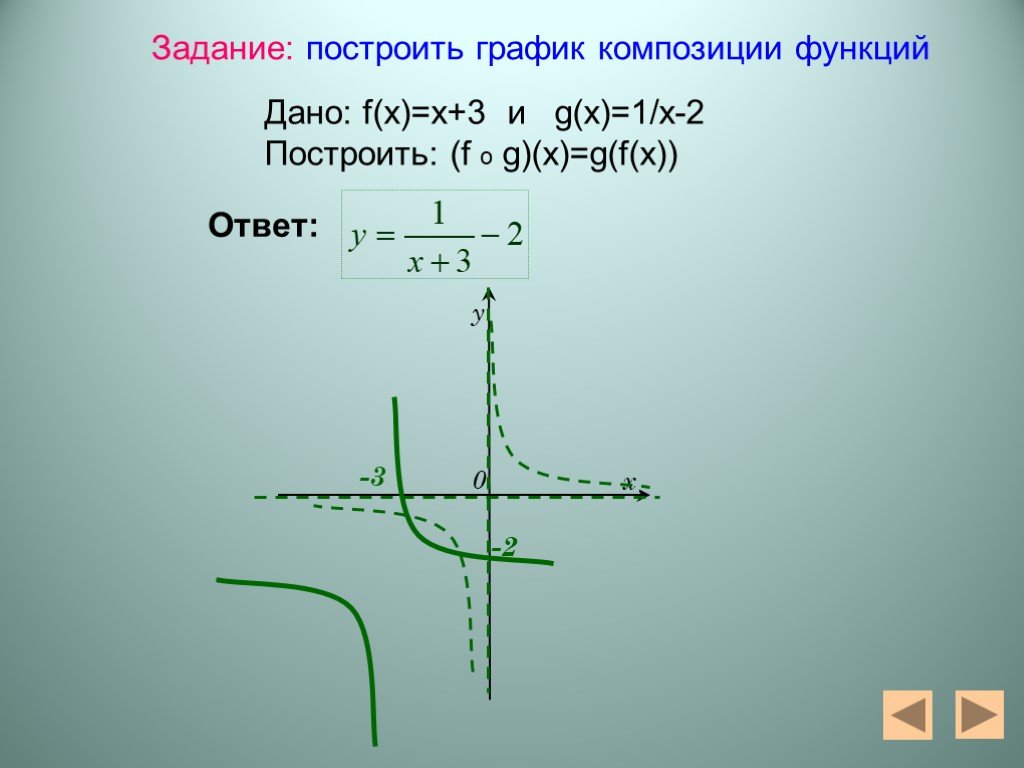
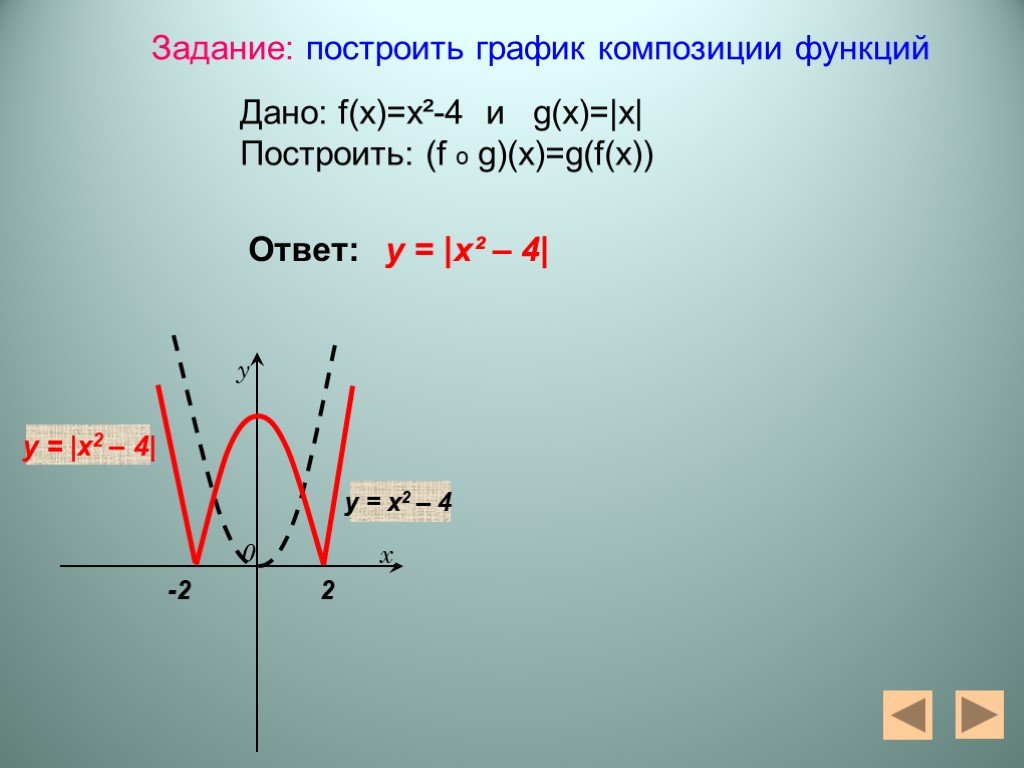
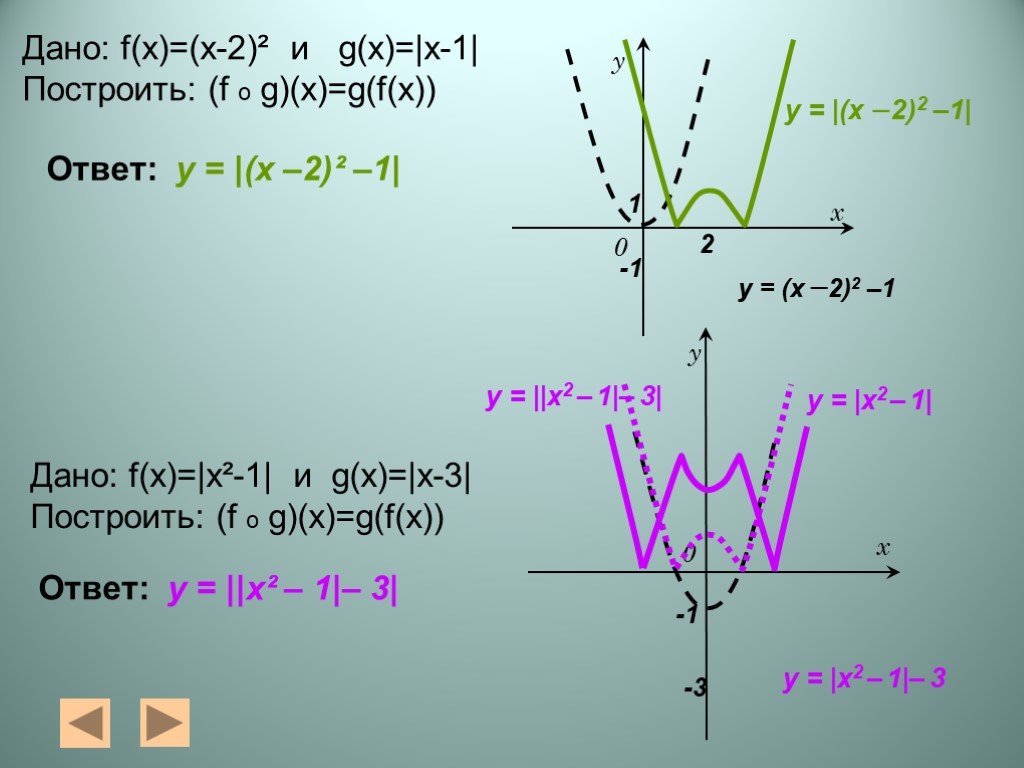
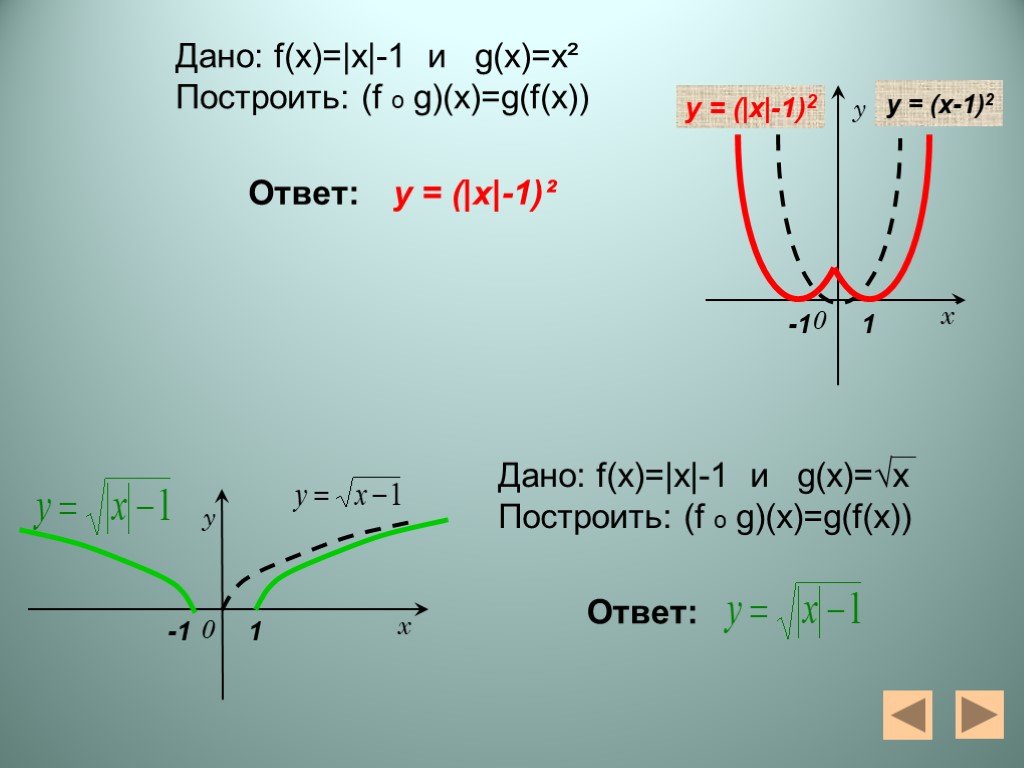
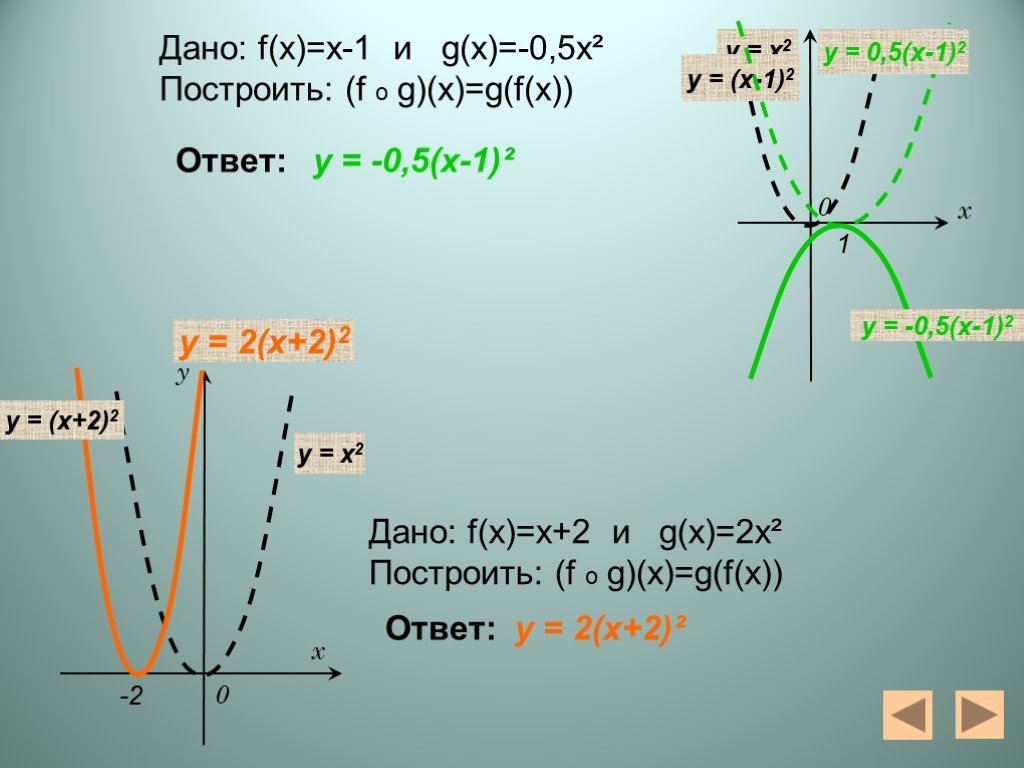
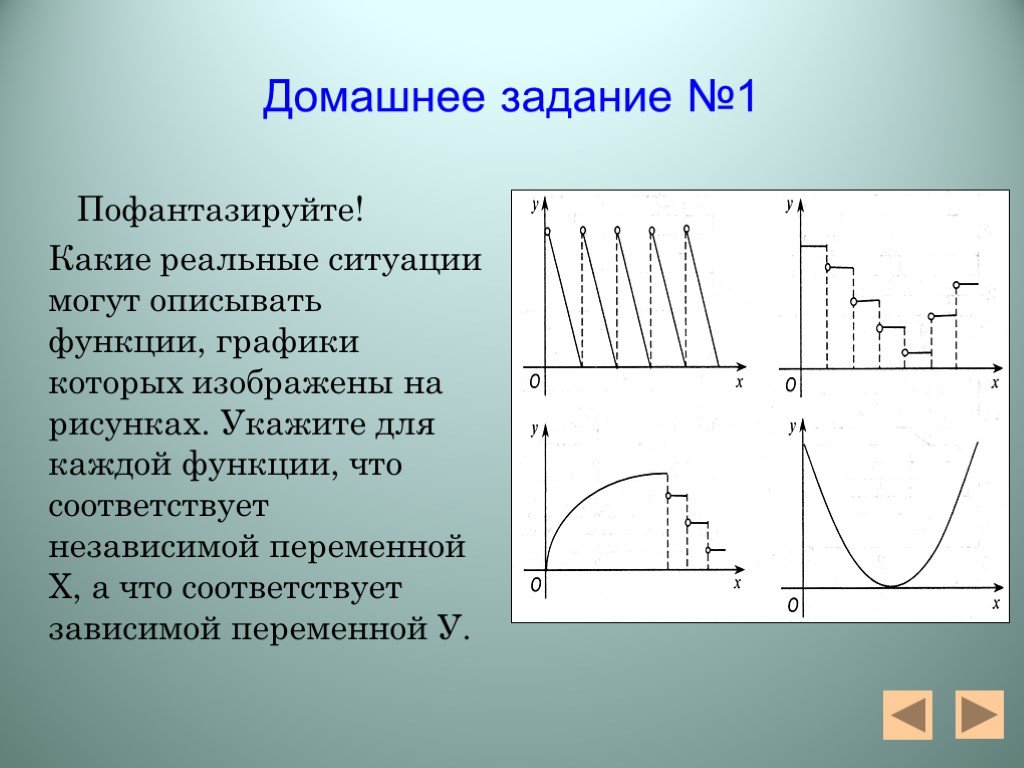
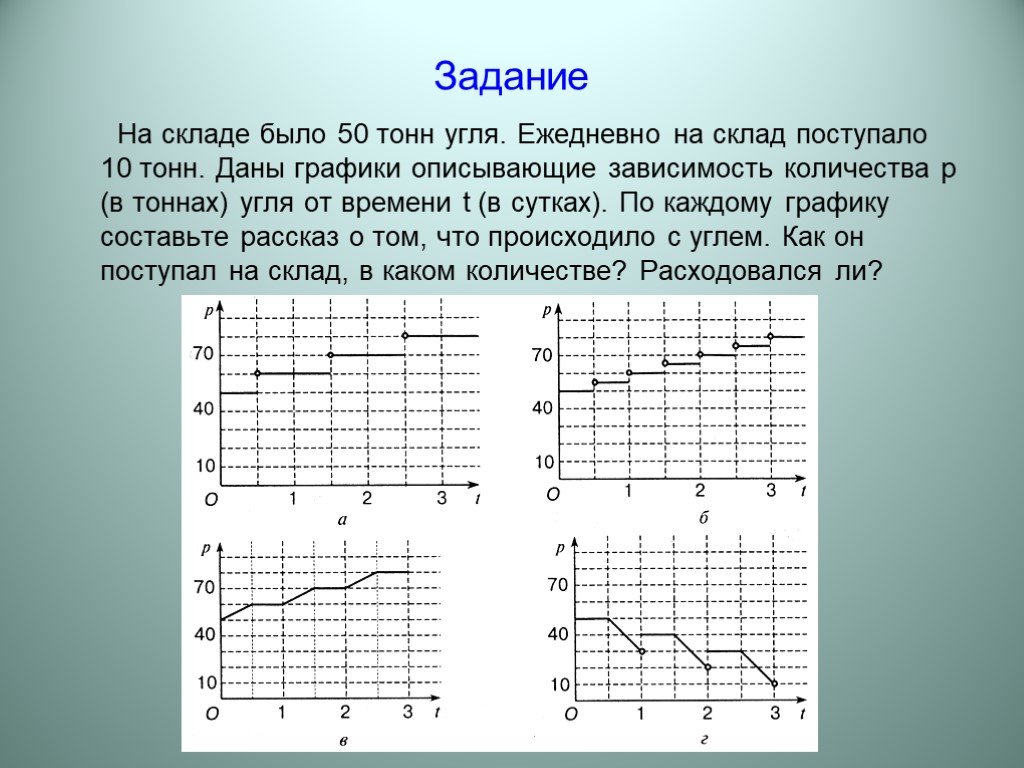
Презентация "Алгебра функций" – проект, доклад
Презентацию на тему "Алгебра функций" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 33 слайд(ов).
Слайды презентации
Список похожих презентаций
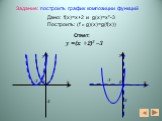
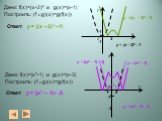
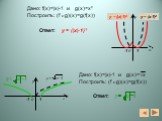
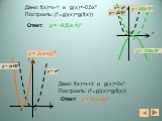
Решение задач на построение графиков алгебраических функций
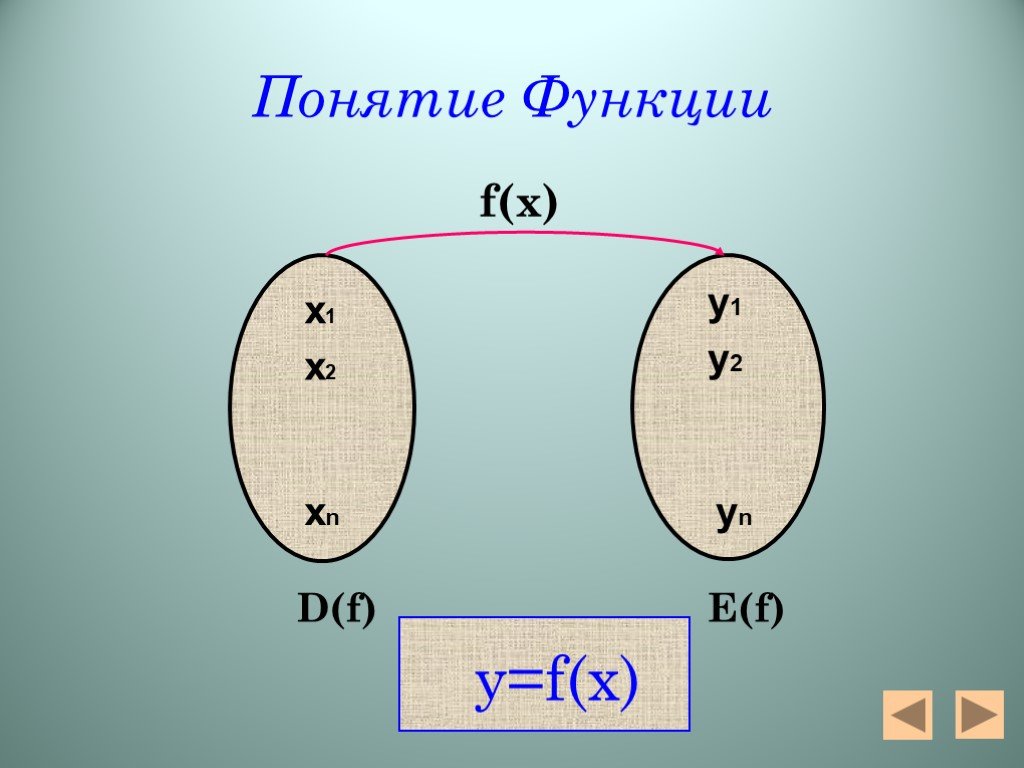
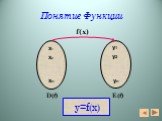
Анализ содержания материала. Кто не знает в какую гавань он плывет, для того нет попутного ветра. Сенека. Главной целью данной темы является: научить ...Функции. Графики функций
1. Задайте формулой функцию, сопоставляющую каждому числу третью степень этого числа. 2. Функция задана формулой Найдите её значение при х = 2. 3. ...Свойства функций
ОБЛАСТЬ ОПРЕДЕЛЕНИЯ ФУНКЦИИ НУЛИ ФУНКЦИИ МОНОТОННОСТЬ (ВОЗРАСТАНИЕ, УБЫВАНИЕ) НАИБОЛЬШЕЕ И НАИМЕНЬШЕЕ ЗНАЧЕНИЯ ОБЛАСТЬ ЗНАЧЕНИЙ ФУНКЦИИ. НУЛИ ФУНКЦИИ ...Свойства тригонометрических функций
I. Свойства функции y=sinx. x 1 0 Масштаб :3 −1 y. 1) Область определения функции – любые числа (x);. 2) Область значений функции – отрезок от ...Производные функций
·. По основному логарифмическому тождеству х =. при всех положительных х, т.е. в этом равенстве справа и слева стоит одна и та же функция, определенная ...Применение свойств тригонометрических функций
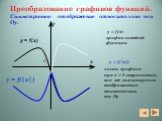
Графики тригонометрических функций. График какой функции изображен на рисунке? Y = cos 0.5 x Y = 2cos x Y = 2cos 0.5x Y = 2 sin x. 1.Y = sin0.5x 2. ...Преобразованиеграфиков функций
Тип урока: обобщение и систематизации знаний, практикум. Цель урока: научить строить графики функций, формулы которых содержит знак модуля. Задачи: ...Преобразование графиков тригонометрических функций
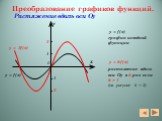
Параллельный перенос на вектор (0; b) вдоль оси ординат: График функции f(x)+b получается параллельным переносом графика f(x) в положительном направлении ...Алгебра Геометрическая прогрессия
Девиз урока: «Нельзя быть любознательным с ленцой…». Личностные цели. Самостоятельно добывать знания Уверенно и грамотно выражать свои мысли на математическом ...Алгебра высказываний. Решение логических задач
Задача 1: Составьте сложное высказывание в словесной форме из простых, заданных математическим формулировкам:. Высказывание А: «Учащийся Иванов хорошо ...Алгебра высказываний
ВОПРОСЫ. 1. Что такое логика? Формальная логика. Математическая логика. 2. Этапы развития логики. 3. Применение математической логики. 4. Алгебра ...Алгебра в 9 классе.
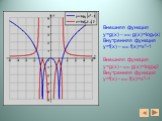
Функция их свойства и графики. Сформулируйте определение чётной функции, определение нечётной функции. Не является ни чётной, ни нечётной. чётная ...Алгебра «Производные»
Структура изучения темы. Приращение аргумента, приращение функции Определение производной Нахождение производной по определению Формулы дифференцирования ...Алгебра «Многочлены»
Цель урока. Систематизировать и обобщить знания учащихся по теме, развивать навыки самопроверки, внимание , усидчивость, терпение, воспитывать аккуратность ...Алгебра
Цель:. - создание условий для ранней психологической адаптации учащихся к переходу на профильное обучение. Гипотеза:. Если скорректировать программу ...Построение диаграмм и графиков функций
Диаграмма (график) — это наглядное графическое представление числовых данных. Основные типы диаграмм. Линейчатая Круговая Линии (график). показывает ...Преобразование графиков тригонометрических функций
Оборудование урока: компьютер, проектор, экран. Цели: Обобщить знания и умения. Развить умение наблюдать, сравнить, обобщать. Воспитать познавательную ...Алгебра и геометрия
История. Женщина обучает детей геометрии. Иллюстрация из парижской рукописи Евклидовых «Начал», начало XIV века. Средние века немного дали геометрии, ...Преобразование графиков функций на координатной плоскости
Эпиграф к уроку. Красота в единстве теории и практики. Цели обучения, воспитания и развития. Рациональные способы построения графиков функций. Развитие ...Алгебра и геометрия
Комплексные числа. ׳. Содержание. § 1. Основные понятия § 2. Геометрическое изображение комплексных чисел § 3. Формы записи комплексных чисел § 4. ...Конспекты
Преобразование графиков тригонометрических функций
Математику уже затем следует учить, что она ум в порядок приводит. М. В. Ломоносов. Урок математики (продолжительность 1ч 20мин). Тема. ...Преобразование графиков тригонометрических функций
Конспект урока по алгебре в 10 классе. Васильева Екатерина Сергеевна. ,. . учитель математики. ОГБОУ «Смоленская специальная (коррекционная). ...Экскурс в мир тригонометрических функций
Славенко Н. В. МОУ СОШ № 32 г. . г Братск. . . Урок обобщающего повторения в 11 классе. . «Экскурс в мир тригонометрических функций». . ...Пpeoбpaзoвaниe гpaфикoв тpигoнoмeтpичecкиx функций
Открытый урок по математике нa тeму «Пpeoбpaзoвaниe гpaфикoв тpигoнoмeтpичecкиx функций». 10 класс. учитель Лукманова Тамара Раисовна. . Пpи ...Решение уравнений нестандартными методами, используя свойства функций
Подготовил и провел учитель математики. . МКОУ «СОШ №1» г. Поворино. . Воронежской области. . Карташова С. А. 2014г. Тема урока:. ...Свойства функций
МОУ «Никифоровская СОШ №2». . Интегрированный урок алгебра – ИВТ с использованием слайдов. ...Взаимное расположение графиков линейных функций
Тема урока: « Взаимное расположение графиков линейных функций». Цель урока:. закрепить умения и навыки нахождения углового коэффициента, познакомить ...Применение свойства монотонности функций при решении уравнений и неравенств
Тамбовское областное государственное автономное образовательное учреждение – общеобразовательная школа – интернат. . «Мичуринский лицей». ...Взаимное расположение графиков линейных функций
Взаимное расположение графиков линейных функций. Учитель: Мисник И.Ю., г Уссурийск. Тип урока: изучение нового материала. Цели урока:. Образовательная. ...Взаимное расположение графиков линейных функций
Муниципальное образовательное учреждение средняя общеобразовательная школа № 33 с углубленным изучением отдельных предметов. Дзержинского района ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:9 июля 2019
Категория:Математика
Содержит:33 слайд(ов)
Поделись с друзьями:
Скачать презентацию