Презентация "Динамическое описание информационных систем" по математике – проект, доклад
Презентацию на тему "Динамическое описание информационных систем" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 23 слайд(ов).
Слайды презентации
Список похожих презентаций
Описание линейных дискретных систем во временной области
Дискретным называется сигнал, дискретный во времени и непрерывный по состоянию. Он описывается решетчатой функцией (последовательностью) x(nT), где ...Сравнение систем быстрого счета при умножении по Трахтенбергу и Берману
Содержание разделов. умножение на девять правила умножения разных чисел по Берману и Трахтенбергу возведение в квадрат двузначных чисел умножение ...Решение систем уравнений
Устно. Что называется решением системы уравнений? Что значит решить систему уравнений? Являются ли пары (1;1) и (-1;3) чисел решением системы {. Х+2у ...Решение систем неравенств с двумя переменными
ПРАВИЛЬНО. НЕПРАВИЛЬНО НАЗАД. 10-5x 0 Ответы: А) x 2 Б) x>2 В) x. . . |x|-3 Б) -33. . . |y| 8 Ответы: А) y -8 Б) -8>у 8 В) у 8 у -8. . . |x-7|. . ...Решение систем линейных уравнений с двумя неизвестными
1. Запишите систему уравнений 5 х – 3 у + 7, х + 2 у = 15. Напишите уравнение, которое получится, если сложить почленно уравнения данной системы. ...Решение систем линейных алгебраических уравнений с помощью определителей
Цель:. изучить свойства определителей и применить их в решении систем линейных алгебраических уравнений. Задачи исследования:. рассмотрение схем вычисления ...Решение неравенств и систем неравенств с одной переменной
Повторение. 1. Какие неравенства соответствуют промежуткам:. 2. Изобразите геометрическую модель промежутков:. 3. Какие неравенства соответствуют ...Представление числовой информации с помощью систем счисления
Система счисления. - это знаковая система, в которой числа записываются по определенным правилам с помощью символов некоторого алфавита, называемых ...Графический способ решения систем уравнений
Построение графика линейной функции. Прямая линия. y = ах + b. х – любое действительное число. 1. Повторение. Построение графика функции обратной ...Графический способ решения систем уравнений
Организационный момент; Подготовка к усвоению новых знаний; Изучение нового материала; Первичная проверка изученного материала; Первичное закрепление ...Графический способ решения систем уравнений
Что является геометрической иллюстрацией уравнения с двумя неизвестными? y-x=2 y+x=2. y=x+2 *A(0;2) *B(-2;0). Уравнение можно рассматривать как формулу, ...Графический способ решения линейных систем уравнений
Линейная функция – это функция вида y=kx+b , в котором k и b - действительные числа. Графиком линейной функции y=kx+b является прямая. Алгоритм ...Графический метод решения систем уравнений с двумя переменными
Обобщить графический способ решения систем уравнений; Сформировать умения графи-чески решать системы уравне-ний второй степени, привлекая известные ...Графический метод решения систем
Что называют системой уравнений? Рассмотрим два линейных уравнения: Y=-x+3 и Y=2x-3 Найдём такую пару значений (x;y), которая одновременно является ...Модели в виде систем одновременных уравнений
Проблемы построения моделей из одновременных уравнений. Авторегрессия Рассмотрим элементарную макроэкономическую модель. В приведенной форме модель ...Графическое решение систем уравнений
Лаборатория «ТРУД». Твори, Решай, Учись, Добивайся с интересом и удовольствием! Руководители лаборатории. Начальник лаборатории: Ноумэн Ноу Мэнович ...Графическое решение систем уравнений
Правило решения системы уравнений графическим способом. Построить графики каждого из уравнений системы. Найти координаты точки пересечения построенных ...Решение неравенств и их систем
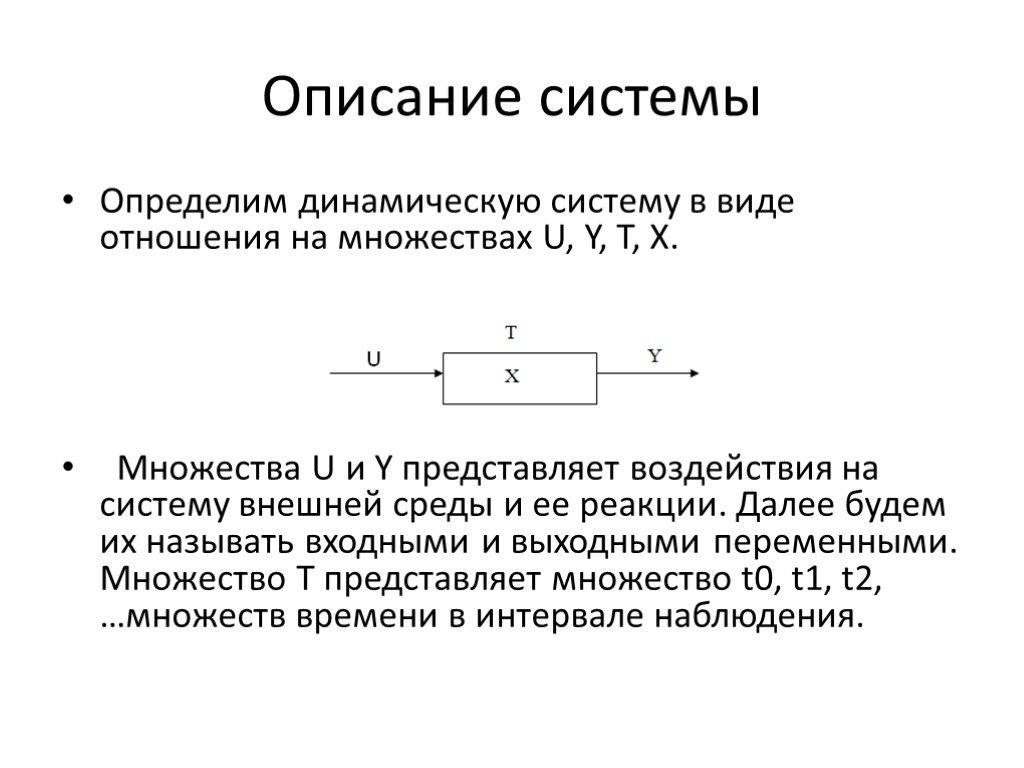
Задание 1. Установите соответствие между неравенствами и промежутками, которые являются их решением. Задание 2. Установите соответствие между промежутками ...Динамические характеристики измерительных систем
Динамические характеристики измерительных систем. Импульсная характеристика системы Частотная характеристика и импульсная характеристика линейной ...Решение систем двух линейных уравнений с двумя переменными различными способами
Цель урока:. Продолжить формирование навыков сознательного выбора способа решения системы Развивать потребность в нахождении рациональных способов ...Конспекты
Решение систем линейных уравнений способом сложения
Муниципальное общеобразовательное учреждение. Пестравская средняя образовательная школа. Пестравского района Самарской области. ...Решение систем неравенств с одной переменной
Муниципальное общеобразовательное учреждение. «Лицей №38» г. Белгород. Урок по теме:. «Решение систем неравенств ...Решение систем линейных уравнений
Разработка урока алгебры. с использованием. интерактивной доски. по теме:. «Решение систем линейных уравнений с двумя переменными». (7 класс). ...Решение систем линейных уравнений
Тема урока: Решение систем линейных уравнений. Цель:. . образовательная: закрепление, систематизация и обобщение знаний о методах решения и исследования ...Решение систем уравнений с одной переменной
Муниципальное автономное общеобразовательное учреждение. «Средняя общеобразовательная школа №16». Города Губкина Белгородской области. ...Решение уравнений, неравенств и систем уравнений
Муниципальное бюджетное общеобразовательное учреждение. основная общеобразовательная школа№8. поселка Садового Муниципального образования Славянский ...Методы решения систем двух линейных уравнений с двумя переменными
План- конспект урока алгебры в 7 классе по теме: «Методы решения систем двух линейных уравнений с двумя переменными». Орг. момент, сообщение ...Решение систем уравнений второй степени
МОУ ООШ c. .Смышляевка. Сергейчева Людмила Алексеевна, учитель математики. Алгебра 9 класс. . . Тема урока "Решение систем уравнений второй ...Графический способ решения систем уравнений
Тема урока:. . Графический способ решения систем уравнений. Тип урока. : Урок изучения нового материала. Цели урока. :. Образовательные. ...Использование метода подстановки для решения систем уравнений
Муниципальное бюджетное общеобразовательное учреждение. «Тимковская основная общеобразовательная школа». Использование . метода . подстановки ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:28 апреля 2019
Категория:Математика
Содержит:23 слайд(ов)
Поделись с друзьями:
Скачать презентацию