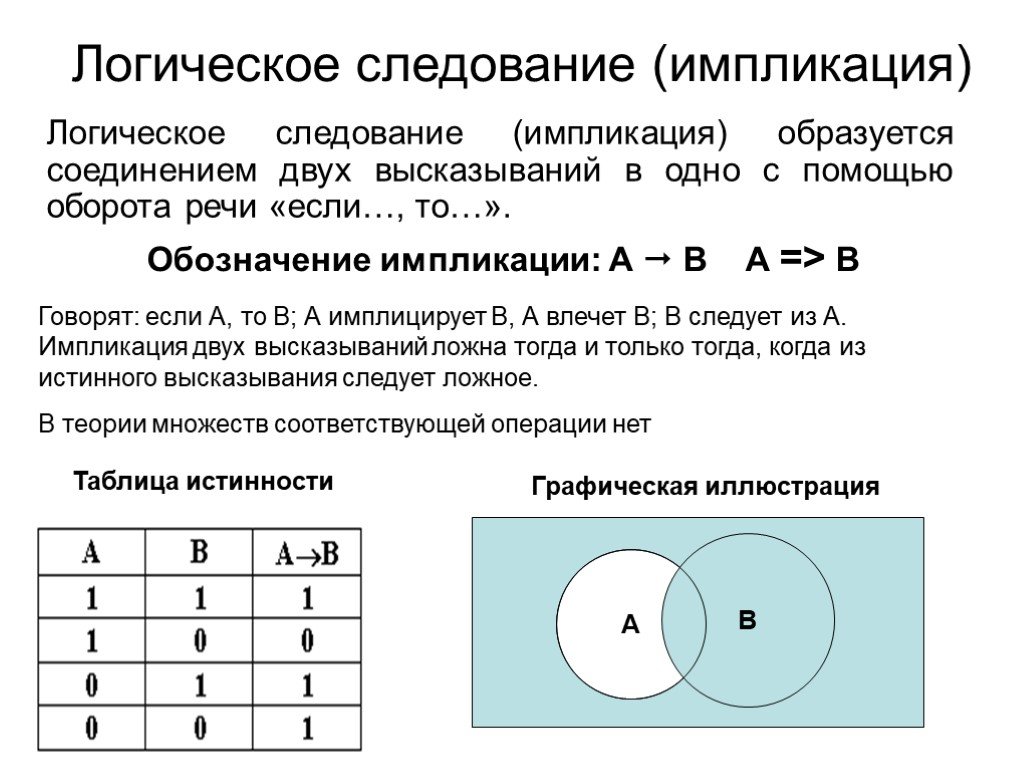
Презентация "Логика как наука" по математике – проект, доклад
Презентацию на тему "Логика как наука" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 18 слайд(ов).
Слайды презентации
Список похожих презентаций
Геометрия как наука
План. Геометрия Разделы геометрии История геометрии Геометрия в космосе Геометрия Лобачевского. Геометрия. Слово геометрия было составлено из двух ...Цилиндр как геометрическая фигура
Цилиндром называется тело, кото-рое состоит из двух кругов, не ле-жащих в одной плоскости и сов-мещаемых параллельным пере-носом, и всех отрезков, ...Уроки обобщения, как средство контроля и закрепления знаний на примере урока "Понятие и основные свойства функций"
Если каждому значению x из некоторого множества чисел ставится в соответствие единственное число y, то говорят, что на этом множестве задана функция ...Симметрия как явление
Цель исследования: Изучить понятие симметрии, виды симметрии Познакомиться с понятием симметрии из литературных источников. Рассмотреть виды симметрии. ...Развитие математики как науки
Удивительно , но. История математики показывает, что в математике существует «странная» традиция, касающаяся выдающихся математических открытий. Революционные ...Поэзия, наука и ученые-математики
Цели проекта. пополнение запаса литературных и историко-научных знаний учащихся; формирование представлений о математике как части общечеловеческой ...Олимпиада как вид внеклассной работы по математике
Олимпиада – соревнование учащихся на лучшее выполнение определенных заданий в какой-либо области знаний. Цели олимпиады:. всестороннее развитие личности ...Муниципальное образовательное учреждение средняя общеобразовательная школа № 78 Краснооктябрьского района г. Волгограда как муниципальный ресурсный центр
20 лет школа № 78 работала в режиме углубленного изучения математики, информатики, биологии. Результаты участия в олимпиадах:. Результаты сдачи ЕГЭ ...Зачем нужна наука геометрия?
Что означает термин геометрия??? Из истории возникновения геометрии. Где изучают геометрию? Виды углов. Виды треугольников. Зачем нужна геометрия??? ...Дробь как одна или несколько равных долей
Частное от деления натуральных чисел можно записать в виде дроби.Числитель дроби – это делимое, а знаменатель - делитель.
пример. знаменатель числитель ...
Дифференцированное обучение как средство повышения уровня учебной мотивации обучающихся на уроках математики
Создание условий дифференцированного обучения:. 1.Разработка индивидуальных стратегий обучения разных детей; 2.Учебно-педагогическая диагностика; ...вычислительная наука
Цель экспресс проекта Данная презентация представляет собой наш глобальный взгляд на эволюцию вычислительной науки и технологии: от Леонардо да Винчи ...Взаимодействие начальной школы и детского сада как условие творческого развития личности
Стартовая работа по математике в 1 классе. Сколько светлых полосок помещается в темной полоске? 2. Какая из фигур больше? Реши те примеры, которые ...Ассоциация, как помощник, при изучении математики
Ассоциация- это мысленная связь между двумя образами. Чем многообразнее и многочисленнее ассоциации, тем прочнее они закрепляются в памяти. Странные, ...Земля как планета
Планета Земля, третья планета по удаленности от Солнца, она является самой крупной по массе среди других землеподобных планет в Солнечной системе. ...Математика-это наука или практика?
Почему в качестве примера логарифмической зависимости в природе я выбрал именно логарифмическую спираль? Известно, что живые существа в природе растут, ...Игра как средство активизации и интенсификации деятельности учащихся
Игра – один из основных видов человеческой деятельности. Основные функции. - развлекательная коммуникативная диагностическая коррекционная социализирующая. ...Неделя математики как способ активизации познавательной деятельности учащихся
развитие личностных качеств обучающихся и активизация их мыслительной деятельности; поддержка и развитие творческих способностей и интереса к предмету; ...Игра как эффективная форма развития познавательного интереса учащихся к математике
Игра как эффективная форма развития познавательного интереса учащихся к математике. Работу выполнила: учитель МОУ СОШ №10 г.Бора Кормич Татьяна Васильевна. ...Подготовлю справочник по геометрии (или как повторить геометрию к экзамену)
1. Остроугольный, тупоугольный и прямоугольный треугольник. Катеты и гипотенуза. Равнобедренный и равносторонний треугольник. 2.Основные свойства ...Конспекты
Синтез искусств как способ обогащения эмоционального мира школьника на уроке музыки
Российская Федерация Тюменская область. Отдел по культуре администрации Сургутского района. Муниципальное образовательное учреждение дополнительного ...Рациональные числа как бесконечные десятичные дроби.
МБОУ гимназия №2 г. Гурьевска. Калининградской области. Конспект урока алгебры в 8-м классе. "Рациональные числа как бесконечные десятичные ...Роль скобок как математического знака
План-конспект урока по теме « Роль скобок как математического знака». . . . . Автор УМК. . . Математика. Арифметика. Геометрия. ...Отрезок. Луч, как часть прямой, построение луча с помощью линейки
Конспект урока математики для 1 класса «. Отрезок. Луч, как часть прямой, построение луча с помощью линейки». Цель:. познакомить с прямой, отрезком, ...Рациональные уравнения как математические модели реальных ситуаций
ПЛАН-КОНСПЕКТ УРОКА Рациональные уравнения как математические модели реальных ситуаций. . ФИО (полностью). . Науменкова Олеся Анатольевна. ...Умножение как действие, заменяющее сложение равных чисел. Знак умножения (.)
Технологическая карта урока математики во 2 классе. . Дата проведения. :13 января, 2015 г. Тема. : «Умножение как действие, заменяющее сложение ...Деление как арифметическое действие. Деление на однозначное число
Автор: Дровосекова Ольга Афанасьевна. Тема разработки: Интегрированный урок математики и английского языка с использованием ИКТ «Деление как арифметическое ...Куб, как частный случай прямоугольного параллелепипеда
Конспект урока математики. 9 класс. Тема: «Куб, как частный случай прямоугольного параллелепипеда». Автор: Старикова Галина Владимировна, учитель ...Медиана как статистическая характеристика
Урок 20. Тема урока:. «Медиана как статистическая характеристика». Предмет:. Алгебра. . Тип занятия:. закрепление изученного материала. . ...Компетентностно-ориентированные задания на уроках математики, как фактор развития предметной грамотности учащихся
Ульянич Елена Васильевна. КГУ «Средняя школа № 17 акимата города Рудного». Мастер – класс. Тема:. «Компетентностно-ориентированные задания на ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:3 апреля 2019
Категория:Математика
Содержит:18 слайд(ов)
Поделись с друзьями:
Скачать презентацию