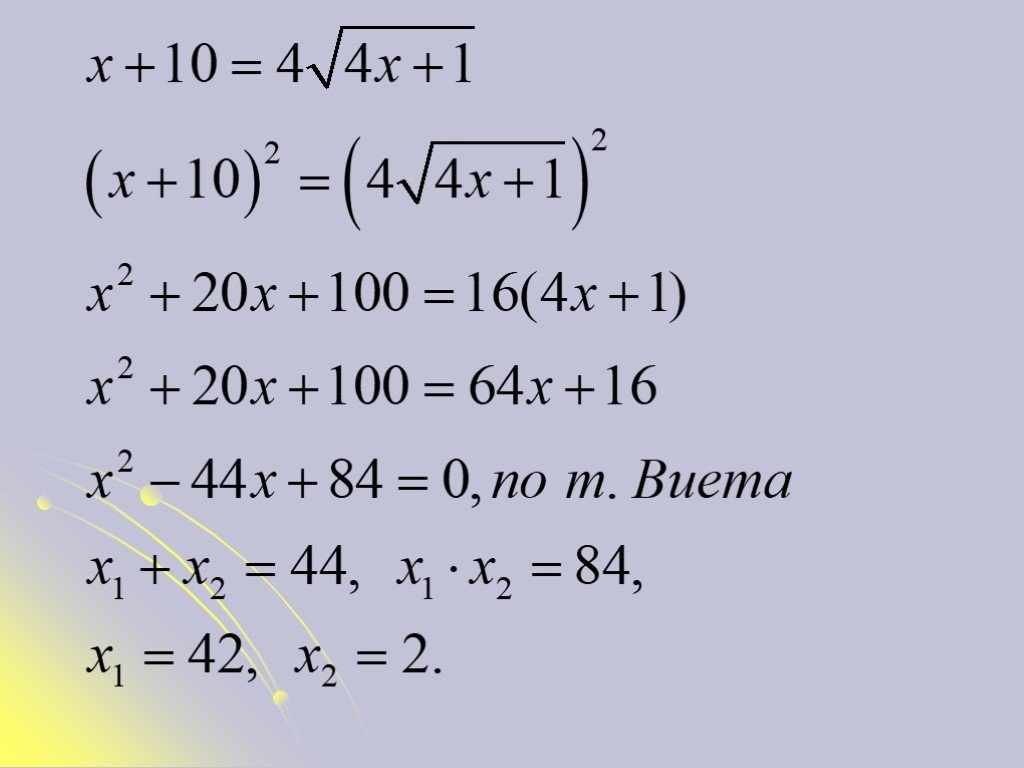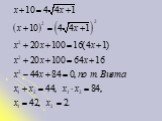Презентация "Примеры иррациональных уравнений" по математике – проект, доклад
Презентацию на тему "Примеры иррациональных уравнений" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 26 слайд(ов).
Слайды презентации
Список похожих презентаций
Решение некоторых иррациональных уравнений
26.12.2017. Необходимые умения и навыки:. 3) умение решать квадратные уравнения;. 4) вычислительные умения и навыки. 1) умение решать линейные уравнения;. ...Примеры решения тригонометрических уравнений
Примеры решения тригонометрических уравнений. Проверочная работа В заданиях 1-6 найдите значения аркфункций в заданиях 7-15 запишите решения простейших ...Решение иррациональных уравнений
ЦЕЛИ. для 1-й группы — развить умения решать иррациональные уравнения на базовом уровне; для 2-й группы — закрепить и развить умения решать иррациональные ...Решение иррациональных уравнений
В данной работе рассматриваются иррациональные уравнения, а также приёмы их решения, которые будут полезны любым ученикам, особенно для подготовки ...Решение иррациональных уравнений
Какие из этих уравнений являются иррациональными? Какие уравнения называются равносильными? Как решать уравнения? Решение:. . Решить устно уравнения. ...Решение иррациональных уравнений
оглавление. Определение Основной метод решения иррациональных уравнений Посторонний корень иррационального уравнения Способы обнаружения постороннего ...Методы решения иррациональных уравнений
Из последнего промежутка найти наименьшее положительное целое число. I Y= II Y= III Y= IV Y= X ≥ 6 X > 0 X > -2 X ≥ 0. Найти область определения. ...Решение иррациональных уравнений
Урок 1 Тема: Решение иррациональных уравнений. Цели: Познакомить учащихся с решениями некоторых видов иррациональных уравнений. Развитие навыка самоконтроля, ...Методы решения иррациональных уравнений
Метод возведения в степень.Пример 1. Ответ: 2. Пример 2. Ответ: 3. Пример 3. Метод составления смешанной системы.
Ответ: 7.
Решение уравнений ...
Решение показательных уравнений
степени n-множителей где n N. n≠1 свойство. . . 2; 8; 16; 27; 32; 64; 81; 100; 125; 128; 216; 243;256; 343; 512; 625; 729, 1024. 1.Представить в виде ...Решение логарифмических уравнений и неравенств.
Логарифмические уравнения. Уравнения, содержащие неизвестное под знаком логарифма или в основании логарифма называются логарифмическими. Решение уравнений, ...Решение линейных уравнений с параметрами
Пусть дано уравнение 2х+3=х+а. Здесь х и а – переменные (неизвестные) величины. Переменная а при решении уравнения считается постоянной (т.е. это ...Решение квадратных уравнений и неравенств
Свойства решений квадратных уравнений. Рассмотрим квадратное уравнение. (1) Дискриминант корни (в случае ). Уравнение. получено из (1) делением на. ...Решение задач с помощью уравнений
Сегодня на уроке. Разминка. Организационный момент. Найди ошибку и реши правильно. Творческая работа. Самостоятельная работа. Физминутка. Как решать? ...Решение уравнений
Меркурий. Решите уравнение. . . . . . . У Я Н Ы Т С П Проверьте себя. Марс. Решите уравнения. 1) 133 + х + 57 = 218, 2) 248 – (у + 128) = 24, 3) (24 ...Решение тригонометрических уравнений
Устная работа. Решите уравнения А) 3 х – 5 = 7 Б) х2 – 8 х + 15 = 0 В) 4 х2 – 4 х + 1= 0 Г) х4 – 5 х2 + 4 = 0 Д) 3 х2 – 12 = 0. Ответы 4 3; 5 0,5 ...Графический способ решения уравнений
1. Если k = -2, b = -4, то функция y = - 2 x - 4. 2. Если k = 2, b = 0, то функция y = 2 x. 3. Если k = 0, b = 3, то функция y = 3. через точку (0 ...Графический способ решения систем уравнений
Построение графика линейной функции. Прямая линия. y = ах + b. х – любое действительное число. 1. Повторение. Построение графика функции обратной ...Графический способ решения систем уравнений
Организационный момент; Подготовка к усвоению новых знаний; Изучение нового материала; Первичная проверка изученного материала; Первичное закрепление ...Графический способ решения систем уравнений
Что является геометрической иллюстрацией уравнения с двумя неизвестными? y-x=2 y+x=2. y=x+2 *A(0;2) *B(-2;0). Уравнение можно рассматривать как формулу, ...Конспекты
Решение иррациональных уравнений и их систем
Тема урока: « Решение иррациональных уравнений и их систем». Цель:. . Знать :. . определение иррациональных уравнений и их систем, методы решения ...Примеры решения тригонометрических уравнений
Урок алгебры в 10-м классе. Тема: «Примеры решения тригонометрических уравнений». Олей Вера Ивановна. учитель математики. Разделы:. . Преподавание ...Применение иррациональных уравнений при решении задач
Полуянова Н.Н. учитель математики. . СОШ № 21 г. Уральск. (алгебра и начала анализа 11 класс, профильный уровень). Конспект открытого ...Решение иррациональных уравнений
Решение иррациональных уравнений. 11 класс. Обобщение темы «Решение иррациональных уравнений»:. Учитель Бакута Е.П. Цели урока. . . Образовательные:. ...Решение иррациональных уравнений
Муниципальное общеобразовательное учреждение. средняя общеобразовательная школа № 31. города Мурманска. Конспект урока. «Решение ...Мир иррациональных уравнений
Методическая разработка занятия. в 11 классе «Мир иррациональных уравнений». Раздел программы:. алгебра и начала математического анализа «Мир ...Методы решения иррациональных уравнений
Урок семинар - практикум в 11-м классе по алгебре и началам анализа. Тема: «Методы решения иррациональных уравнений». Цели и задачи урока:. . ...Методы решения иррациональных уравнений
Урок по теме «Методы решения иррациональных уравнений» в 11 классе. . Бекиш И.И. учитель математики, 1 категории,Успенская средняя школа, район ...Методы решений иррациональных уравнений
Сивак Светлана Олеговна. Урок – игра. «Методы решений иррациональных уравнений». Открытый урок по алгебре и ...Методы решения иррациональных уравнений
Конспект урока – практикума с презентацией по теме. «Методы решения иррациональных уравнений». . Аннотация:. . . Урок алгебры и начала анализа ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:12 сентября 2019
Категория:Математика
Содержит:26 слайд(ов)
Поделись с друзьями:
Скачать презентацию