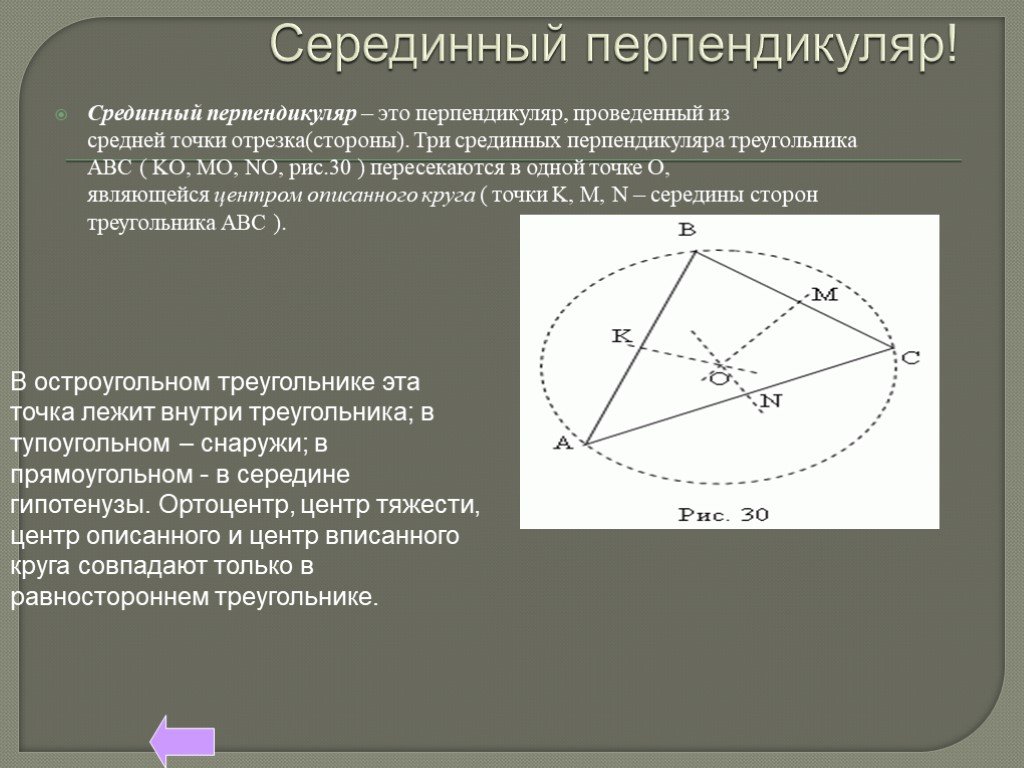
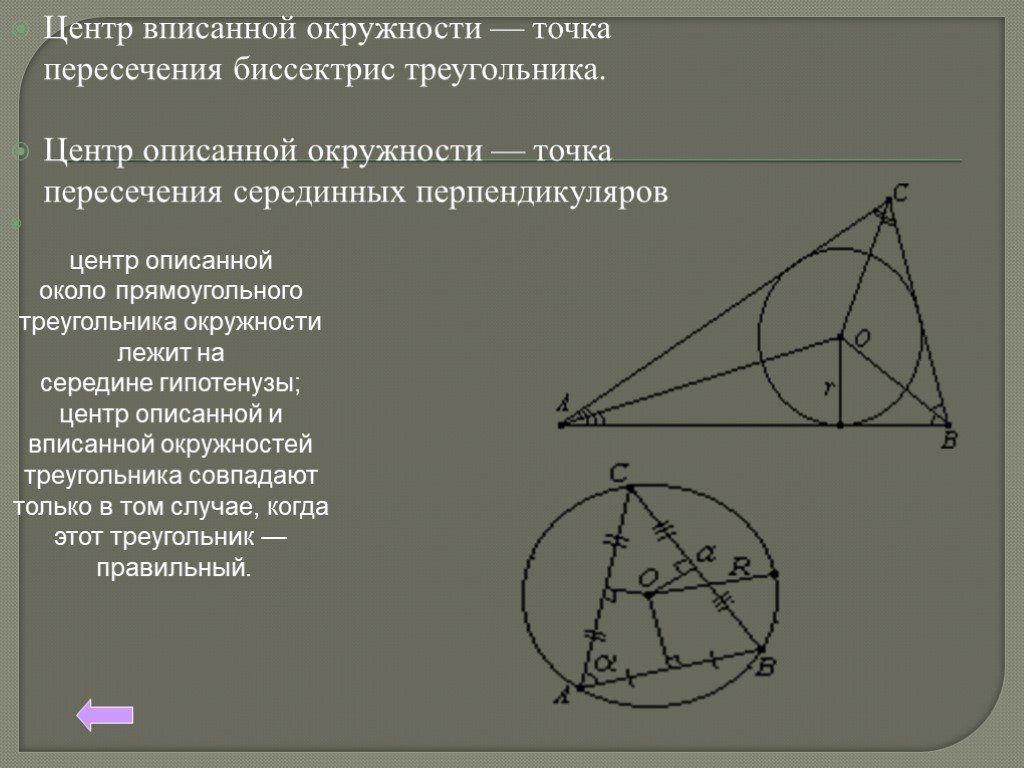
Презентация "Подготовлю справочник по геометрии (или как повторить геометрию к экзамену)" – проект, доклад
Презентацию на тему "Подготовлю справочник по геометрии (или как повторить геометрию к экзамену)" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 11 слайд(ов).
Слайды презентации
Список похожих презентаций
Анализ учебников по геометрии
Хорошо известно, что успехи в обучении школьников во многом зависят от содержания и структуры учебника, по которому они занимаются. По одним учебникам ...А Какую геометрию знаешь ты?
План презентации: Краткие биографические данные Основные виды геометрии Геометрия Евклида Геометрия Лобачевского Геометрия Римана Применение Всех ...Анализ контрольной работы по математике на тему "Натуральные числа и шкалы"
Натуральные числа и шкалы. 5 к л а с с № 1. Цели деятельности учителя. Главная дидактическая цель : организовать деятельность учащихся, направленную ...альбом по математике
Формирование базовых знаний, умений и навыков должно быть связано с творческой деятельностью, с развитием индивидуальных задатков учащихся, их познавательной ...Аксиомы геометрии
Евклид и его труды III в до н.э. Такой подход, когда сначала формируются исходные положения-аксиомы, а затем на их основе путем логических рассуждений ...«Задачи по математике»
Успех каждого – это шаг к успеху всего класса. Реши примеры 5 ·8 5·5 4·6 8·8 25-5 36-6. 48-8 99-9 6·10 50·10 4·10 7·100. =40 =25 =24 =64 =20 =90 =60 ...Авторалли по городам математики
Цель: Закрепить навык выполнения действий, возведения чисел в квадрат и куб, закрепить формулы пути и площади. Расширение кругозора учащихся, развитие ...2 класс Тренажер по математике
Выбери героя, нажав на него, с кем хочешь проверить свои знания! 7 + 7 18 12 14. 7 + 9 16 15. 7 + 4 11. 7 + 8 17. 7 + 6 13. 10 + 6. 10 + 8 10. 10 ...«Уравнения по математике»
17.10.12. Классная работа. Тема: «Уравнения». Решение уравнений. Математические фокусы. Составление равенств. «Секретная» сказка. «Математику нельзя ...«Решение задач по математике»
10 февраля. В классе. Задача условие вопрос решение ответ. Быстро и правильно считать. Правильно записывать решение задачи. Кричать и сердиться, когда ...«Решение задания С1 ЕГЭ по информатике и ИКТ»
2 балла. Решение задания С1 ЕГЭ по информатике и ИКТ. Кунина В.В. область I область II. 0 x y y = x+2 y2 + x2 = 25 y2 + x2 25 y 0 x 0 область ...«Олимпийский» задачник по математике
Если вы хотите научиться плавать, то смело входите в воду, а если хотите научиться решать задачи — решайте их Д. Пойа. Если мы действительно что-то ...«Моя математика» - задачи на нахождение целого или части
МАТЕМАТИКА 1 3 4 5 7 6 8 9 0. Работа с числовым рядом. http://www.bajena.com/ru/kids/mathematics/sum-mathematics.php. 1. Прочитайте текст справа и ...«Лабораторные работы по геометрии»
Вписанная и описанная окружности. Цель работы: Проверить при построении в любой ли треугольник можно вписать окружность и вокруг любого ли треугольника ...Анализ обучающих программ по математике 1-4 класс
Интерактивная математика для 1-4 классов. Программа фирмы Marco Polo Group. Описание продукта: Интерактивный тренажер по математике для начальной ...Авторские задачи по математике и физике, составленные по повести Н.В. Гоголя «Ночь перед Рождеством
Методологическая основа: Класс арифметических задач огромен. Учащиеся старших классов обычно пытаются решать такие задачи алгебраически, так как владеют ..."Магические квадраты – магия или наука
Милостивый государь, я составил магический квадрат 21-го порядка! - А я рамочный 23-го! (из переписи Баше де Мезириака и Рене Декарта). Составление ...Апробация инструментария диагностических исследований профессиональной компетентности учителей начальных классов по математике
Проводится в соответствии приказом управления образования и науки области от 18.03.2010 №841 «О проведении апробации инструментария диагностического ...«Скалярное произведение векторов» геометрия
Таблица значений для углов, равных 300, 450, 600. Заполните таблицу. Формулы приведения. sin( )= cos( )= -. Проверка д.з. № 1039 Диагонали квадрата ...«Конус» геометрия
История изучения геометрического тела конус. С именем Евклида связывают становление александрийской математики (геометрической алгебры) как науки. ...Конспекты
Видеть и слышать, или как не потеряться в мире информации
Конспект – сценарий урока, разработанного учителями МОУ Брызгаловская СОШ Ивановой Е.Б. и Колпаковой Л.В. Тема: «Видеть и слышать, или как не потеряться ...Во сколько раз одно число больше или меньше другого
Тема :. Во сколько раз одно число больше или меньше другого. Цель:. Формировать умения и навыки решать задачи на нахождение, во сколько раз одно ...Виртуальное путешествие по Америке при помощи математических вычислений
Негосударственное частное образовательное учреждение для детей дошкольного и младшего школьного возраста «Прогимназия № 63 ОАО «РЖД». ...Алгебраические выражения. Подготовка к экзаменам
Государственное бюджетное специальное (коррекционное) образовательное учреждение для обучающихся, воспитанников с ограниченными возможностями здоровья ...Больше или меньше
. Подробный конспект урока. Организационная информация. Тема урока. . Больше или меньше. . . Предмет. . Математика. . . ...Больше или меньше
Тема урока: Больше или меньше. I. Образовательные цели:. закрепить умения и навыки. сравнения натуральных чисел. . записи результата ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:7 июня 2019
Категория:Математика
Содержит:11 слайд(ов)
Поделись с друзьями:
Скачать презентацию