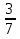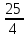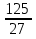Конспект урока «Степень с рациональным показателем» по алгебре для 11 класса
Учитель математики: Нашкенова А.Н. Майбалыкской средней школы
План-конспект урока по теме «Степень с рациональным показателем»
(алгебра, 11 класс)
Цели урока:
-
Расширить и углубить знания учащихся о степени числа; ознакомление учащихся с понятием степени с рациональным показателем и их свойствами;
-
Выработать знания, умения и навыки вычислять значения выражений путем использования свойств;
-
Продолжить работу по развитию умений анализировать, сравнивать, выделять главное, определять и объяснять понятия;
-
Формировать коммуникативные компетентности, умения аргументировать свои действия, воспитывать самостоятельность, трудолюбие.
Оборудование: учебник, раздаточные карточки, ноутбук, презентационный материал Power Point;
Тип урока: урок изучения и первичного закрепления новых знаний.
План урока:
1.Орг. момент. - 1 мин.
2.Мотивация урока.- 2мин
3.Актуализация опорных знаний. - 5 мин.
4.Изучение нового материала. - 15 мин.
5.Физкультминутка - 1 мин.
6.Первичное закрепление изученного материала - 10 мин
7.Самостоятельная работа. - 7 мин.
8.Домашнее задание. - 2 мин.
9.Рефлексия – 1 мин.
10.Итог урока. – 1 мин.
Ход урока
1. Организационный момент
Эмоциональный настрой на урок.
Желаю работать, желаю
трудиться,
Желаю успехов сегодня добиться.
Ведь в будущем всё это вам
пригодится.
И легче в дальнейшем вам будет
учиться (Слайд №1)
2.Мотивация урока
Действия возведения в степень и извлечения корня, как и четыре арифметических действий, появились в результате практической потребности. Так, наряду с задачей вычисления площади квадрата, сторона а которого известна, встречалась обратная задача: «Какую длину должна иметь сторона квадрата, чтобы его площадь равнялась в. В 14-15 веках в Западной Европе появляются банки, которые давали деньги в рост князьям и купцам, финансировали за большие проценты дальние путешествия и завоевательные походы. Чтобы облегчить расчеты сложных процентов составили таблицы, по которым сразу можно было узнать, какую сумму надо уплатить через п лет, если была взята взаймы сумма а по р % годовых. Уплачиваемая сумма выражается формулой: s= а(1 +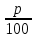 )п .Иногда деньги брались в долг ни на целое число лет, а например, на 2 года 6 месяцев. Если через 2.5 года сумма а обратиться в aq, то через следующие 2.5 лет она увеличиться еще в q раз и станет равной aq2. Через 5 лет: а=(1 +
)п .Иногда деньги брались в долг ни на целое число лет, а например, на 2 года 6 месяцев. Если через 2.5 года сумма а обратиться в aq, то через следующие 2.5 лет она увеличиться еще в q раз и станет равной aq2. Через 5 лет: а=(1 +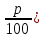 5 , поэтому q2= (1 +
5 , поэтому q2= (1 +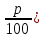 5 и значит q=
5 и значит q= 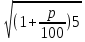
( Слайд 2).
Так возникла идея степени с дробным показателем.
3.Актуализация опорных знаний.
Вопросы:
1.Что означает запись; ап
2. Что такое а?
3. Что такое п?
4. а -п =?
5.Запишите в тетради свойства степени с целым показателем.
6.Какие числа относятся к натуральным , целым, рациональным? Изобразить их с помощью кругов Эйлера. (Слайд 3)
Ответы: 1. Степень с целым показателем
2. а- основание
3. п- показатель степени
4. а -п =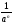
5.Свойства степени с целым показателем:
am *an = a(m+n);
am : an = a(m-n) ( при a не равном нулю);
(am)n = a(m*n);
(a*b)n = an *bn;
(a/b)n = (an)/(bn) (при b не равном нулю);
a1 = a;
a0 = 1 ( при a не равном нулю);
Эти свойства будут справедливы для любых чисел a, b и любых целых чисел m и n.
6.1,2,3, …- положительные числа – множество натуральные числа –N
0,-1,-2,-3,.. число О и отрицательные числа –множество целые числа - Z
Q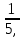 ,
,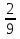 – дробные числа (отрицательные и положительные) – множество рациональные числа - Q
– дробные числа (отрицательные и положительные) – множество рациональные числа - Q
Z
N
Круги Эйлера (слайд 4)
4. Изучение нового материала.
Пусть . а- неотрицательное число и требуется возвести его в дробную степень 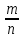 . Вам известно равенство ( аm )n = аm n (слайд 4) , т.е. правило возведения степени с степень. В приведенном равенстве предположим, что m =
. Вам известно равенство ( аm )n = аm n (слайд 4) , т.е. правило возведения степени с степень. В приведенном равенстве предположим, что m = 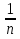 , тогда получим: (а
, тогда получим: (а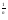 )п= а
)п= а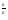 =а (слайд 4)
=а (слайд 4)
Отсюда можно заключить, что является а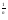 корнем п- й степени от числа а, т.е. а
корнем п- й степени от числа а, т.е. а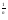 =
=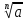 . из этого следует , что (ап)
. из этого следует , что (ап) 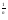 =
= 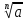 п=а(слайд 4).
п=а(слайд 4).
Следовательно а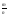 =( а
=( а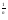 ) m=( а m)
) m=( а m) 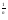 =
= 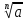 m. (слайд 4).
m. (слайд 4).
Таким образом, имеет место следующее равенство: а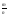 =
=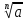 m(слайд 4)
m(слайд 4)
Определение: степенью неотрицательного числа а с рациональным показателем 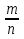 , где
, где 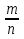 - несократимая дробь, называется значение корня п –й степени из числа ат.
- несократимая дробь, называется значение корня п –й степени из числа ат.
Следовательно, по определению а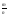 =
=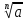 m (слайд 5)
m (слайд 5)
Разберем пример 1: Напишите степень с рациональным показателем в виде корня п-й степени :
1)5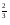 2)3,7-0,7 3) (
2)3,7-0,7 3) (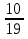 )
)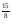 (слайд 6)
(слайд 6)
Решение: 1) 5 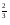 =
=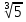 2 =
2 = 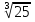
2) 3,7-0,7 =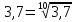 -7
-7
3) (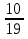 )
) 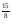 =
=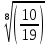 (слайд 7)
(слайд 7)
Над степенями с рациональным показателем можно производить действия умножения, деления, возведения в степень и извлечения корня по тем же правилам, как степенями с целым показателями и степенями с одинаковыми основаниями:
а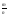
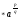 = а
= а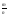 +
+ 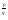
а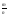
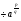 = а
= а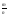 -
- 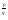
(а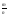 )
) 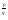 = а
= а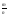 *
* 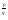
(а*в)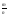 = а
= а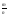 * в
* в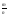
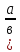 )
)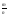 =а
=а /в
/в
где п,q – натуральные , т, р- целые числа. (слайд 8)
5.Физкультминутка
Отвели свой взгляд направо,
Отвели свой взгляд налево,
Оглядели потолок,
Посмотрели все вперёд.
Раз – согнуться – разогнуться,
Два ─ согнуться – потянутся,
Три – в ладоши три хлопка,
Головою три кивка.
Пять и шесть тихо сесть.
И снова в путь! (слайд 9)
6.Первичное закрепление изученного материала:
Страница 51, № 90, № 91 – выполнить в тетради самостоятельно,
с проверкой у доски
7.Самостоятельная работа
| Вариант 2 | |
| Запишите следующие степени с дробными показателями в виде корней | |
| 15 | 23 |
| (-14) | (-71) |
| а | а |
| (а +в) | (а-6) |
| (9-3а) | (в+2) |
| (х- у) | (3+2а) |
(Слайд 10)
| Вариант 2 | |
| Вычислите: | |
| 27 | 81 |
| 0,64 | 0,49 |
| 125 | 64 |
| 81 | 16 |
| ( | ( |
(Слайд 11)
Выполнить самостоятельную работу с взаимопроверкой.
Ответы:
| Вариант 2 | |
| Запишите следующие степени с дробными показателями в виде корней | |
| 15 | 23 |
| (-14) | (-71) |
| а | а |
| (а +в) | (а-6) |
| (9-3а) | (в+2) |
| (х- у) | (3+2а) |
(Слайд 11)
| Вариант 2 | |
| Вычислите: | |
| 27 | 81 |
| 0,64 | 0,49 |
| 125 | 64 |
| 81 | 16 |
| ( | ( |
(Слайд 12)
Итак, сегодня на уроке мы познакомились с понятием степени с рациональным показателем и научились записывать в виде корней , применять основные свойства степеней при нахождении значений числовых выражений.
8.Домашнее задание: №92,№ 93 Информация о домашнем задании
9.Рефлексия
(Слайд 13)
10.Итог урока:
- в чем сходство и различие степени с целым показателем и степени с дробным показателем? (сходство: все свойства степени с целым показателем имеют место и для степени с рациональным показателем;
различие: степени )
- перечислите свойства степени с рациональным показателем
Урок сегодня завершён,
Дружней вас не сыскать.
Но каждый должен знать:
Познание, упорство, труд
К прогрессу в жизни приведут.
Спасибо за урок! (слайд 14)
Раздаточный материал для самостоятельной работы
| Вариант 2 | |
| Запишите следующие степени с дробными показателями в виде корней | |
| 15 | 23 |
| (-14) | (-71) |
| а | а |
| (а +в) | (а-6) |
| (9-3а) | (в+2) |
| (х- у) | (3+2а) |
| Вариант 2 | |
| Вычислите: | |
| 27 | 81 |
| 0,64 | 0,49 |
| 125 | 64 |
| 81 | 16 |
| ( | ( |
Замечание. Презентационный материал снабжен системой гиперссылок, которые рекомендуется использовать учителю во время урока для обеспечения необходимой последовательности представления материала. Кроме того, на слайдах предусмотрено последовательное появление материала, управляемое учителем, что позволит организовать проблемную беседу.
Здесь представлен конспект к уроку на тему «Степень с рациональным показателем», который Вы можете бесплатно скачать на нашем сайте. Предмет конспекта: Алгебра (11 класс). Также здесь Вы можете найти дополнительные учебные материалы и презентации по данной теме, используя которые, Вы сможете еще больше заинтересовать аудиторию и преподнести еще больше полезной информации.

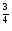
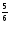
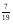
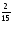
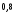
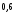
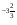
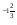
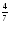

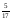
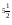
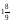
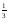
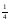
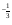
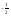
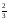
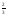
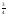
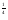
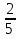 )
)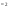
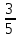 )
)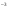
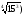
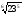 )
)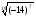 )
)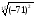 )
)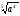 )
)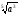 )
)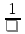 )
)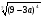 )
)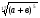 )
)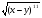
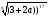
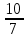 =1
=1