Конспект урока «Решение показательных уравнений с параметрами» по алгебре для 11 класса

Скачать конспект (0.19 Мб) Смотреть похожие конспекты

Решение показательных уравнений с параметрами

Развитие и образование ни одному человеку не могут быть даны или сообщены. Всякий кто желает к ним приобщиться должен достигнуть этого собственной деятельностью, собственными силами, собственным напряжением.

Адольф Дистервег

Цели:

Обобщить знания и умения по применению методов решения показательных уравнений.
Развивать умение наблюдать, обобщать, анализировать математические ситуации.
Воспитывать такие качества личности, как познавательная активность, самостоятельность, упорство в достижении цели.

Задачи:

Образовательные задачи:

- изучить методы решения показательных уравнений с параметрами;

- применить обобщенные знания, умения и навыки в новых условиях.

Развивающие задачи:

- создать содержательные и организационные условия для развития умений решать нестандартные показательные уравнения и находить различные способы их решения,

- побуждать учащихся к самоконтролю, взаимоконтролю, самоанализу своей деятельности.

Воспитательные задачи:

- формирование у учащихся познавательного интереса к математике, элементов культуры общения;

- побуждать учащихся к преодолению трудностей в процессе умственной деятельности.

Оборудование: компьютер, проектор, на столах учащихся оценочные листы, карточки с заданиями для самостоятельной работы, карточки с заданиями для работы в группах.

Тип урока: урок комплексного применения знаний и навыков.

Работа учащихся состоит из трех этапов. Итоги своей деятельности ребята фиксируют в оценочных листах.

План урока:

Устный опрос.
Самостоятельная работа.
Изучение нового.
Работа в группах.
Домашнее задание.

Оценочный лист учащегося

Фамилия ____________________________________________________

Имя _________________________________________________________

№ П/п

Этапы работы	Достижения	Количество баллов
1	Устный опрос.	Воспроизведение опорных знаний
2	Самостоятельная работа	Умения учащихся применять разные методы при решении показательных уравнений. (ЕГЭ В₇ и С₂)
3	Работа в группах.	Работа поискового характера. Умение решать нестандартные уравнения. (ЕГЭ С₃)

Итоговое количество баллов ____________

Оценка ____________

Самооценка за урок зависит от суммы набранных баллов на всех этапах.

Критерии оценок:

“5” 14 – 15 баллов
“4” 12 – 13 баллов
“3” 9 – 11 баллов.

Ход урока

1. Организационный момент

Учитель ориентирует учеников в работе с оценочными листами.

- Перед вами на партах лежат оценочные листы, в которых вы будете выставлять себе баллы за проделанную работу. Самооценка за урок зависит от суммы набранных баллов на всех этапах.

- На предыдущих уроках мы изучили свойства показательной функции, рассмотрели методы решения показательных уравнений. Как вы думаете, в чем будет заключаться наша задача на сегодняшнем уроке? (Применять полученные знания при решении показательных уравнений.)

- Вспомним свойства показательной функции.

2. Устный опрос (10мин.)

Слайд № 1.

а) Укажите множество значений данных функций: у = 3•2^х- 5; у = 5^х+1; у = 5^¦х¦+1; у = 0,5^{sin x}; у = ; у = .

Слайд № 2.

б) Определите, каким методом будем решать каждое уравнение:

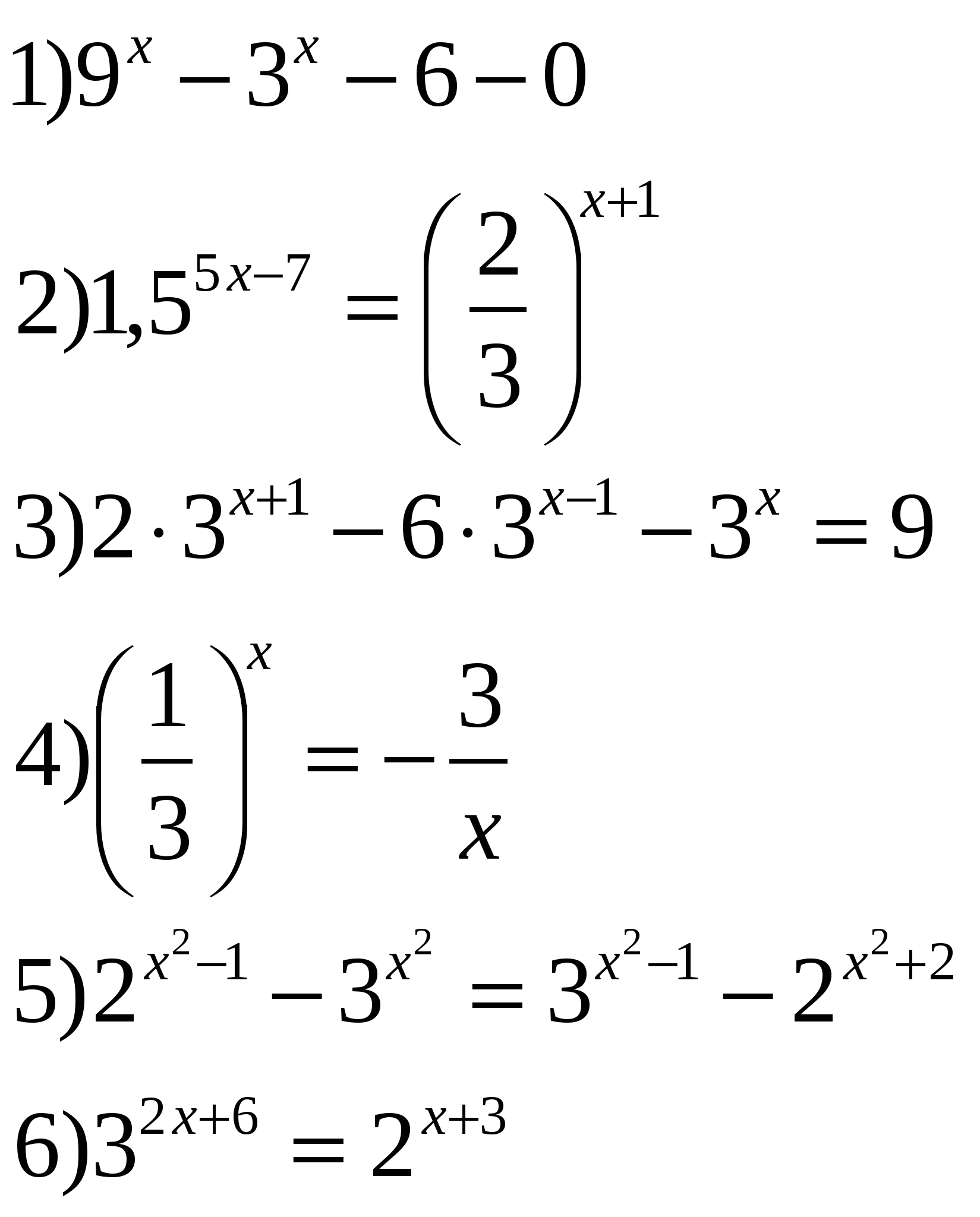
Слайд № 3.

в) При каком условии уравнение

- имеет один корень;

- два корня;

- не имеет корней?

-Какие основные методы мы используем для решения показательных уравнений?

Слайд № 4. Методы решения показательных уравнений.

Метод приведения степеней к одному основанию.
Вынесение общего множителя.
Метод замены переменной.
Метод почленного деления.
Метод группировки функций.
Функционально-графический метод.

3. Самостоятельная работа (10 мин.)

- Используйте ваши знания при решении самостоятельной работы.

- У вас на столах лежат карточки с заданиями для самостоятельной работы. Решите данные уравнения в течение 10 минут.

Карточка для сам. работы.

Вариант № 1.

Вариант № 2.

3) Укажите абсциссы точек пересечения графиков функций

Слайд № 5.

Проверка самостоятельной работы

Вариант№1. Вариант №2.

3,11 1) 1
0 2) – 2,0
-1 3) 2

Критерии оценки самостоятельной работы

1 уравнение – 3 балла

2 уравнения – 4 балла

3 уравнение – 5 баллов

(Вернуться к слайду № 4)

4. Изучение нового материала (10 мин.)

Показательные уравнения с параметрами

- Мы изучили основные методы решения показательных уравнений. Однако, понятно, что на этом изучение темы не закончено. И поскольку мы готовимся к ЕГЭ, то логично предположить, чем же мы будем заниматься далее в рамках этой темы.

(Уравнениями с параметрами, нестандартными уравнениями из части С
и т.д.)

- Да, интересно рассмотреть блок уравнений, требующих исследования, нестандартных подходов – это уравнения из части С, такие как уравнения с параметрами, уравнения содержащие знак модуля и так далее.

- И я предлагаю вам рассмотреть уравнение вида , где f(х) – показательная функция.

- При каких значениях параметра а уравнение имеет один корень?

Решение.

- Каким методом будем решать это уравнение?

(Так как 4^х = (2^х)² , то это уравнение можно переписать в виде

и введением новой переменной t = 2^х , t >0 свести к квадратному уравнению)

- Учитывая, что t >0, сформулируйте задачу, которую нам предстоит решить.

(При каких значениях параметра а уравнение имеет один положительный корень.)

1) При а = 3 имеем линейное уравнение ,

которое имеет единственный корень . Так как t >0, то а = 3 является решением.

2) Если , D = 0, t > 0

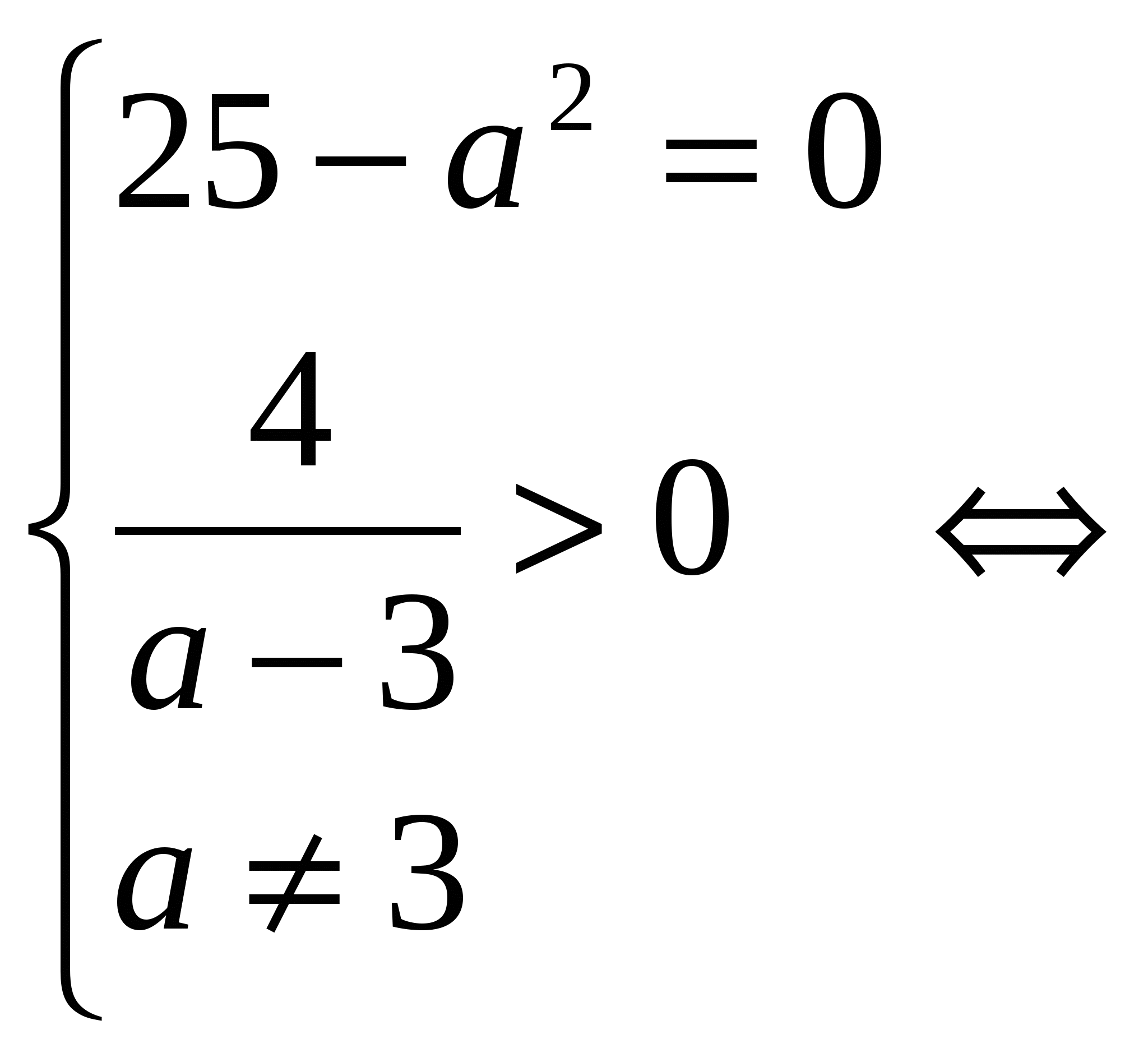
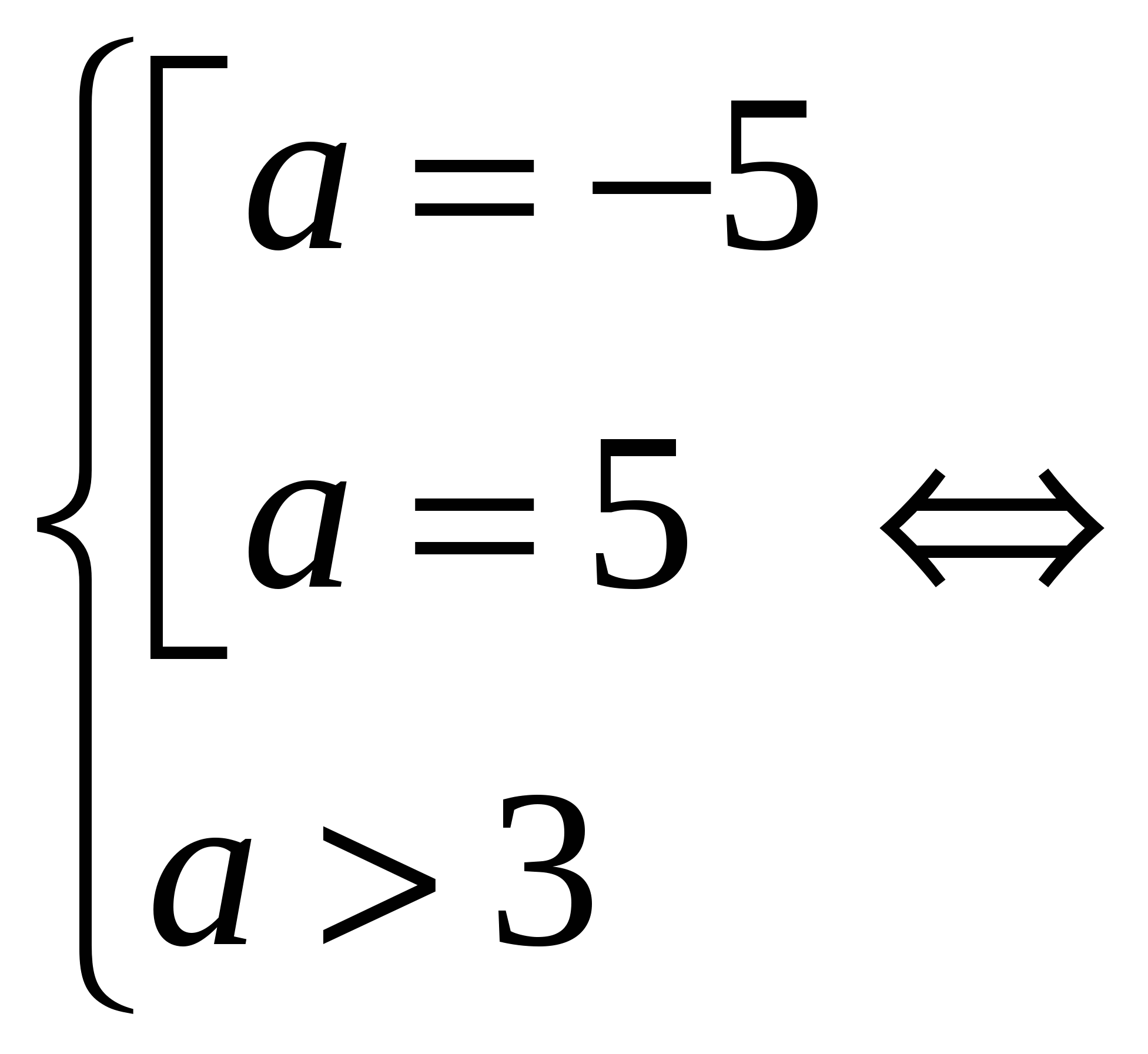
3) Если , D > 0, t₁ t₂ > 0

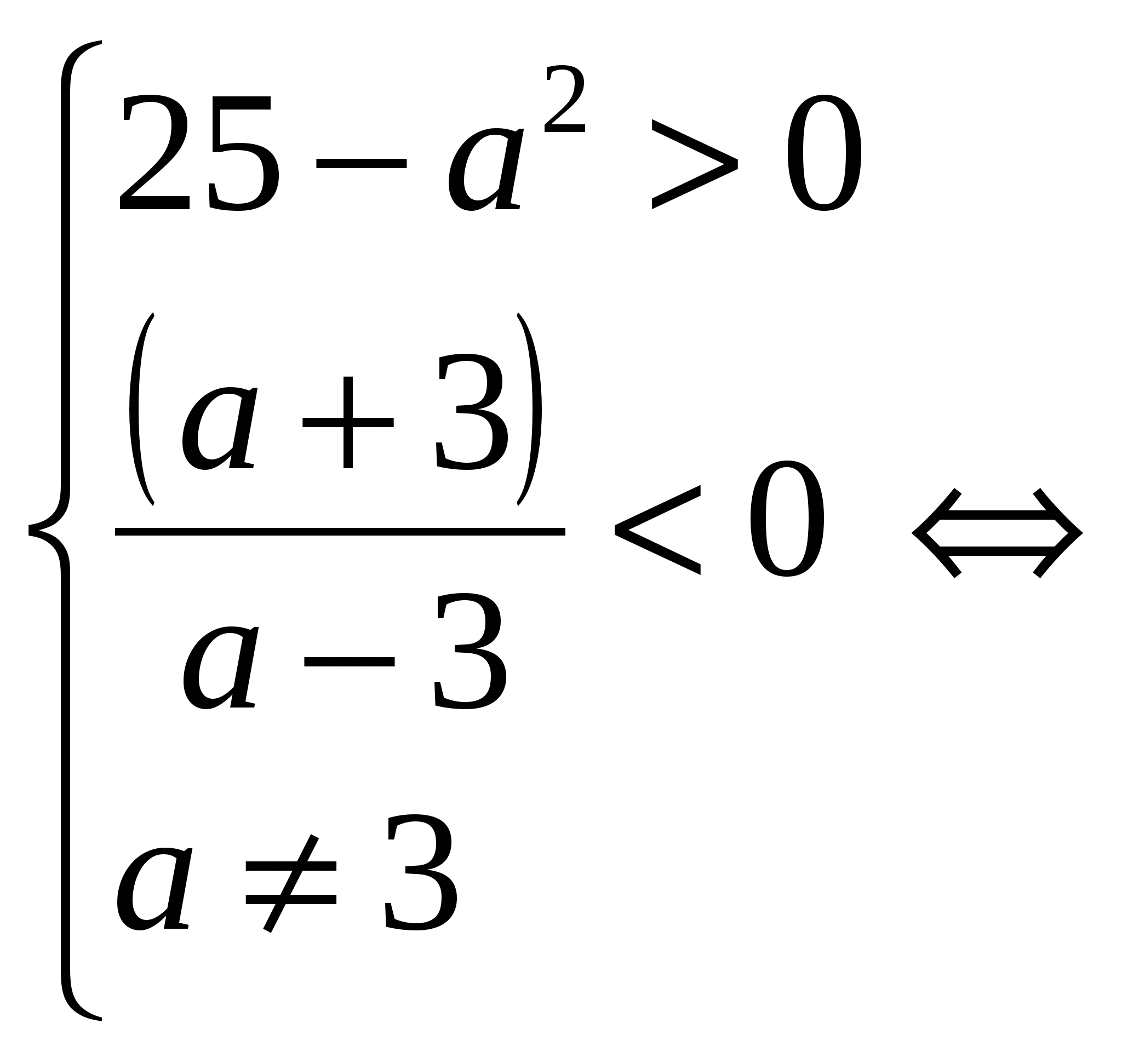
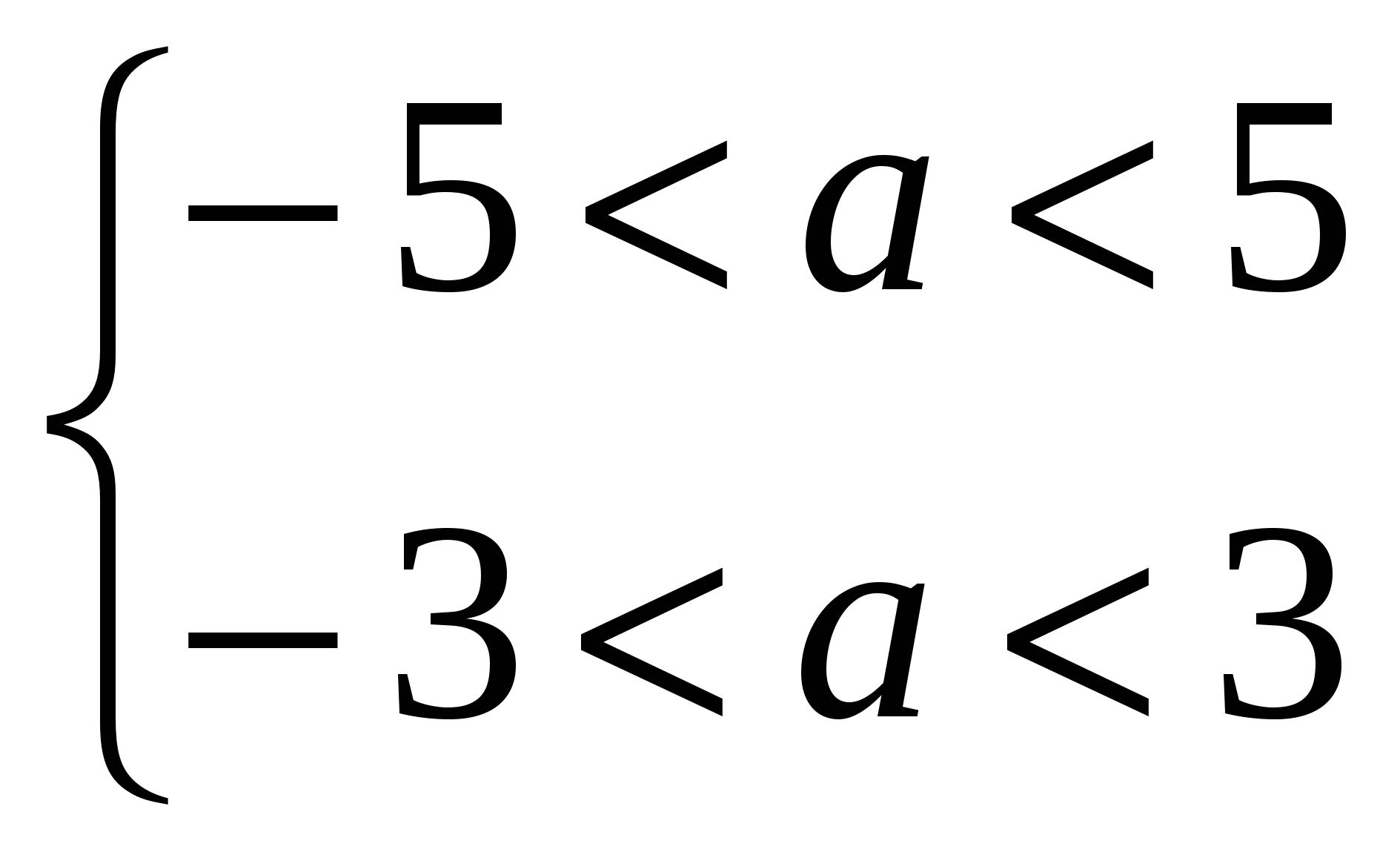
4) При , D > 0, t₁ = 0, t₂>0

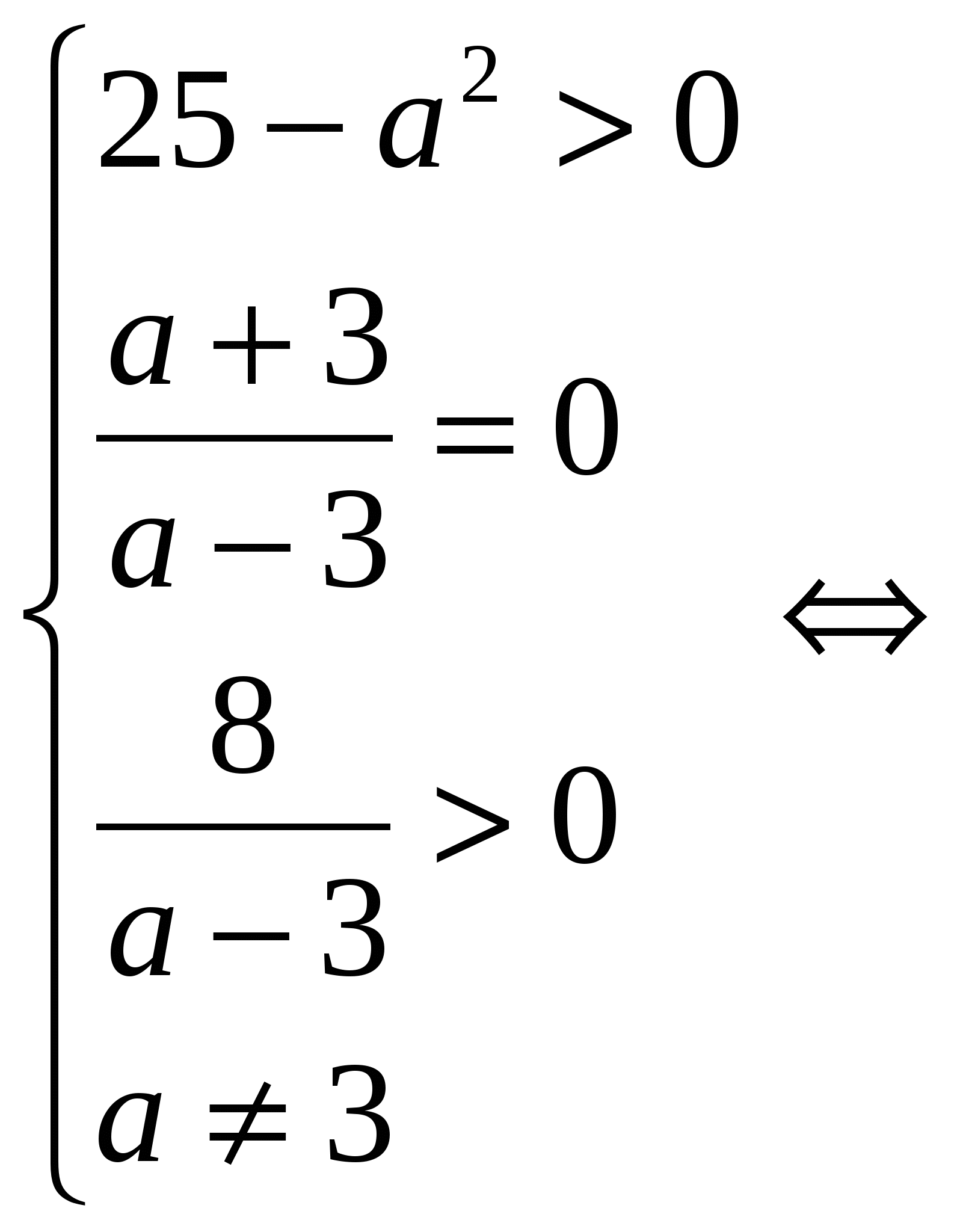
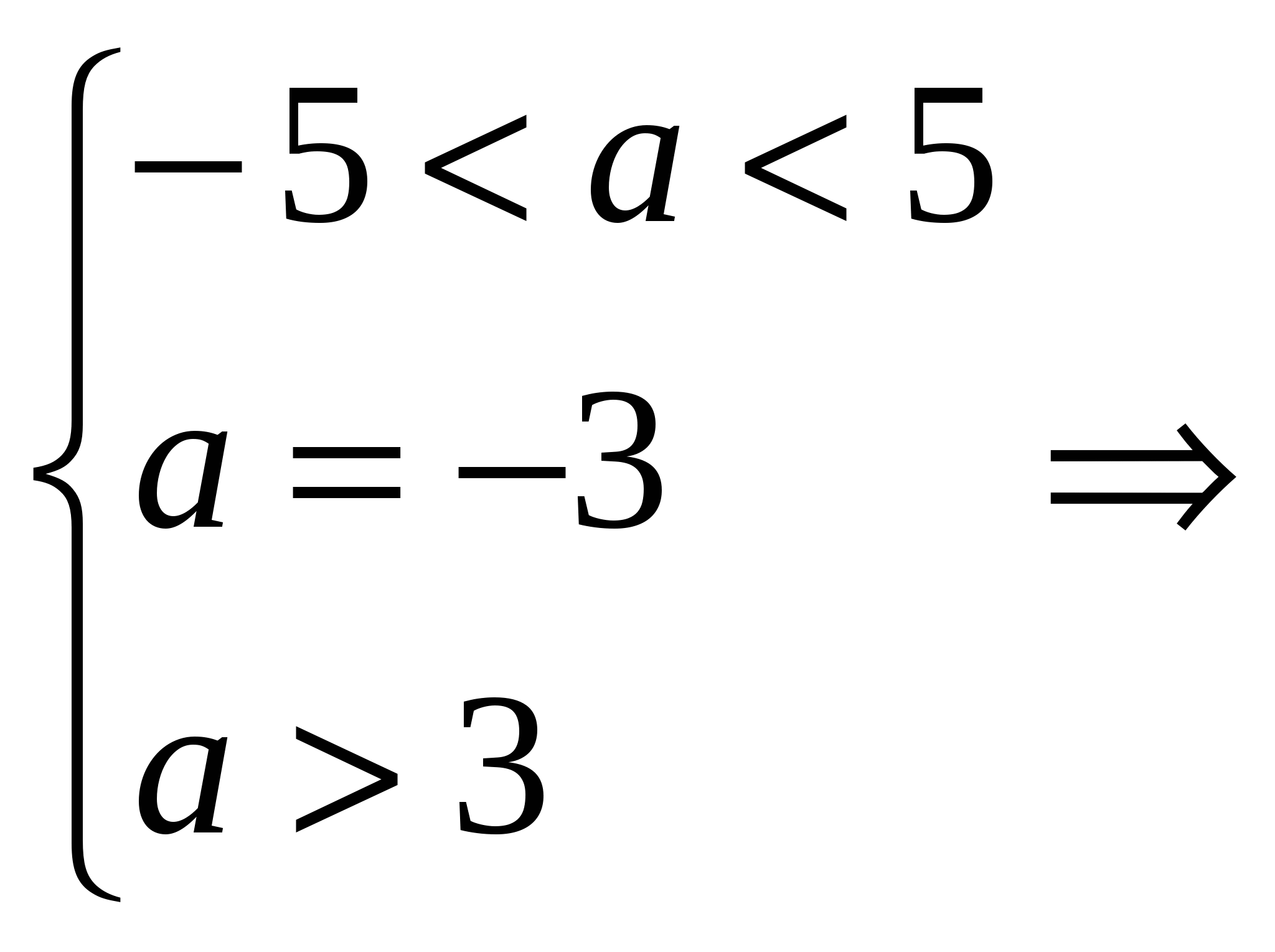решений нет

Объединяя множества значений параметра а, получаем, что исходное уравнение будет иметь один корень при .

Ответ: .

Слайд № 6.

Основные этапы решения:

1) а = 3

2) , D = 0, t > 0

3) , D > 0, t₁ t₂ > 0

4) , D > 0, t₁ = 0, t₂>0

5. Работа в группах (10 мин.)

- А сейчас вы решите уравнение с параметром, разбившись на группы.

Задание на карточке.

При каких значениях уравнение имеет единственное решение.

(1)

Область допустимых значений параметра :

Замена. (2)

Уравнение (1) имеет единственное решение при условии, что уравнение (2) имеет единственный положительный корень.

Проверим: одно решение.

Уравнение (1) имеет единственное решение, если уравнение (2) имеет два корня, но один из них нуль, а второй положителен.

Проверим эти значения, подставив их в исходное уравнение.

- нет решений, или - нет решений.

- одно решение.

Уравнение (1) имеет единственное решение, если уравнение (2) имеет два корня различных знаков. Для этого достаточно выполнение неравенства

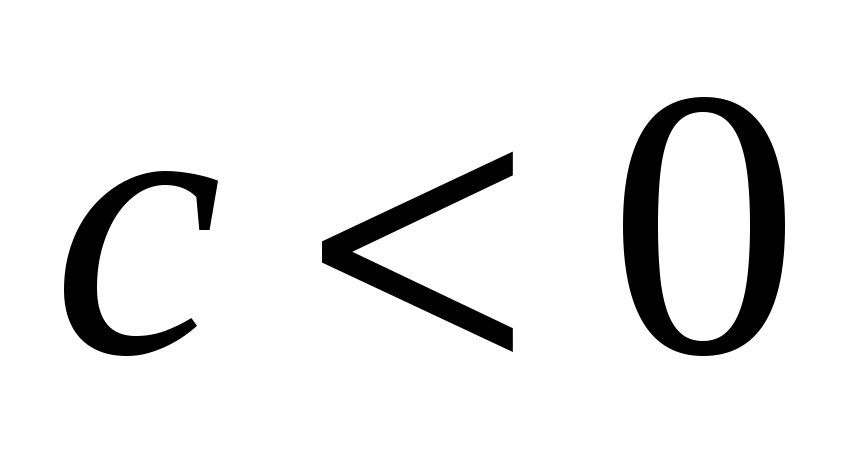
Ответ: При уравнение имеет единственное решение.

- Результаты работы каждого члена группы оцениваются консультантом.

Консультанты сдают оценочные листы учителю, который выставляет оценки в журнал.

6. Итог урока

- Полезен ли вам был сегодняшний урок?

- Как вы оцениваете свою работу на уроке?

7. Домашнее задание (на карточках)

1) При каких значениях параметра а уравнение имеет единственное решение?

2) При каких значениях параметра а уравнение имеет два различных корня?

3) Указать число решений уравнения в зависимости от параметра р.

Литература

Алгебра и математический анализ. 11 кл.: Учеб. для углубл. изуч. математики в общеобразоват. учреждениях/ Н.Я. Виленкин, О.С. Ивашев-Мусатов, С.И. Шварцбурд. – 12-е изд., испр., – М.:Мнемозина, 2009. – 72-74 с.
Задачник по математике для учащихся средней школы и поступающих в вузы: Учеб. пособие. – М.: Московский лицей, 2002. – 72 с.
Математика. Подготовка к ЕГЭ-2010/ Под редакцией Ф.Ф. Лысенко, С.Ю. Кулабахова. – Ростов-на-Дону: Легион-М, 2009. – 235 с.
Математика: Пособие для поступающих в вузы. Пермь: Изд-во Перм. Ун-та, 2000. – 124с.
Нестандартные задачи по математике. Алгебра: Учеб. Пособие для учащихся 7 – 11 кл. Челябинск: «Взгляд», 2004. – 145с.

Здесь представлен конспект к уроку на тему «Решение показательных уравнений с параметрами», который Вы можете бесплатно скачать на нашем сайте. Предмет конспекта: Алгебра (11 класс). Также здесь Вы можете найти дополнительные учебные материалы и презентации по данной теме, используя которые, Вы сможете еще больше заинтересовать аудиторию и преподнести еще больше полезной информации.

Скачать конспект (0.19 Мб) Смотреть похожие конспекты

Список похожих конспектов

Информация о конспекте

Ваша оценка: Оцените конспект по шкале от 1 до 5 баллов

Дата добавления:26 июля 2016

Категория:Алгебра

Классы:

11 класс

Поделись с друзьями:

Скачать конспект

Навигация по сайту

Мы в социальных сетях

Конспект урока «Решение показательных уравнений с параметрами» по алгебре для 11 класса

Список похожих конспектов

Решение показательных уравнений

Решение показательных уравнений

Решение показательных уравнений

Решение показательных уравнений

Решение показательных уравнений

Решение показательных уравнений

Решение показательных уравнений и неравенств в 11 профильном классе

Решение показательных уравнений различными способами

Свойства показательной функции. Решение показательных уравнений и неравенств

Методы решение показательных уравнений

Логарифмы и решение логарифмических уравнений

Логарифмы и решение логарифмических уравнений

Квадратные уравнения. Основные понятия. Решение неполных квадратных уравнений

Графическое решение квадратных уравнений

Решение квадратных уравнений

Решение квадратных уравнений в среде программирования QBasic 8 класс

Решение логарифмических уравнений

Решение логарифмических уравнений

Методы решения показательных уравнений

Методы решения показательных и логарифмических уравнений и неравенств

Информация о конспекте

Конспекты из категории

ПРОГРЕССИИ

Теорема Виета

Решение систем уравнений второй степени с параметром графическим способом

Нестандартные методы решения уравнений и неравенств. Использование области определения функций

Квадратный трехчлен

Решение неравенств с одной переменной

СИСТЕМЫ УРАВНЕНИЙ

Итоговое повторение. Решение заданий по теме « Уравнения

Формулы куба суммы и куба разности двух выражений

Решение квадратных уравнений