Конспект урока «Решение показательных уравнений» по алгебре для 11 класса
Методическая разработка урока алгебры в 11 классе
Тема урока: Решение показательных уравнений.
Аудитория: 11 класс
Место урока в теме: урок знакомства с методами решения показательных уравнений, на предыдущем уроке введено определение показательного уравнения, представлен способ решения простейших показательных уравнений (приведение к одному основанию), ранее закончена тема «Показательная функция».
Цели урока: обучающие: на конец урока учащиеся:
-
формулируют определение показательного уравнения;
-
умеют распознавать показательные уравнения среди различных уравнений;
-
выбирают способы решения показательных уравнений;
-
решают показательные уравнения изученными ранее способами (с помощью учителя, по образцу);
развивающие:
-
развитие логического мышления, умения анализировать, сопоставлять;
-
формирование грамотной математической речи.
Формы, методы и приемы: фронтальная работа, работа в группах, поисковый метод.
Ход урока:
-
Мотивация учащихся. Постановка целей урока.
Учитель: Вы знаете, что предстоящий экзамен по математике проверяет в том числе умение решать уравнения. Вам известны многие виды уравнений и на прошлом уроке мы познакомились еще с одним - с простейшими показательными уравнениями. Исходя из своего опыта решения уравнений вы, конечно, понимаете, что класс показательных уравнений не ограничивается простейшими уравнениями. А это значит, что...
Учащиеся пробуют сформулировать тему и содержание урока.
Учитель: Да, сегодня нам предстоит познакомится с другими “представителями класса показательных уравнений” и, конечно, попытаться найти способы их решения.
Сначала давайте вспомним, какие уравнения нам известны и какими способами мы их решаем. Перед вами уравнения, ваша задача – определить вид каждого уравнения и назвать способ его решения.
-
х 2 + 7х + 6 = 0 8) 3х + 1 = 2 – х
-
3six 2 x – 5sin x – 2 = 0 9)
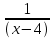 +
+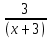 = 2
= 2 -
2х 4 - 27х2 + 81 = 0 10) 2х3 – 18х – 3х2 + 27 = 0
-
3х 2 - 8x = 0 11) 73х – 15 =
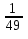
-
2 2 – х = 8 12)
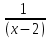 = х + 2
= х + 2 -
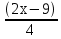 =
=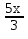 13) sin 2x + cos 2x = 0
13) sin 2x + cos 2x = 0 -
sin2 x + 2sin x cos x – 3cos 2 х = 0 14) 2sin x cos x + sin x = 0
Учащиеся: уравнение 1) - квадратное, решается по формулам (через дискриминант); 4) – неполное квадратное уравнение, решается вынесением за скобку общего множителя (разложение на множители) и применением правила о равенстве нулю произведения нескольких множителей; уравнение 2) – тригонометрическое, с помощью замены сводится к квадратному; Уравнение 3) – биквадратное, также решается сведением к квадратному с помощью замены; уравнение 6) – линейное; уравнения 5), 8) и 11) – это показательные уравнения, т.к. переменная находится в показателе степени. 5) и 11) можно отнести к простейшим показательным уравнениям и решить их сведением обеих частей к одному основанию. Однако к 8-му уравнению этот способ решения применить нельзя. Уравнение 7) – тригонометрическое, однородное , для его решения применяется почленное деление на sin2 x или на cos2 x, таким образом получается тригонометрическое уравнение, сводящееся к квадратному. Уравнение 12) – дробно-рациональное, можно решить по свойству пропорции. Но его можно еще решить графическим способом, который, надо заметить, не всегда может дать точный ответ. Уравнение 9) тоже дробно-рациональное, для решения используется приведение к общему знаменателю и свойство пропорции. Уравнение 13) – однородное тригонометрическое, способ решения – почленно разделить на cos2x. Уравнение 10) – уравнение третьей степени, можно попробовать разложить на множители и применить правило равенства нулю произведения нескольких множителей. Уравнение 14) – тригонометрическое, также решается разложением на множители.
Учитель: Молодцы! Верно названы все виды уравнений, способы их решения. Вы, наверное, заметили, что одни и те же способы решения предлагались для разных видов уравнений. Так может быть эти способы могут помочь и при решении показательных уравнений? Я предлагаю сейчас обсудить этот вопрос.
2. Работа в группах. (класс заранее поделен на группы по 3-4 человека)
Каждой группе предлагается набор уравнений. Группе необходимо найти универсальный способ решения всех предложенных уравнений. Время работы в группах оговаривается заранее (не более 15 минут). После завершения работы представители групп должны познакомить класс с найденными способами решения уравнений (на примере решения одного уравнения).
Наборы уравнений для групповой работы:
1 группа: 2х – 1 = √ х
3х+2 = - х + 3
![]() = 2х + 5
= 2х + 5
2 группа: 4х-3 + 4х = 260
5х+1 + 5х + 5х-1 = 31
7 х - ![]() = 6
= 6
3 группа: 2 2х – 3*2х + 2 = 0
9 х + 2 * 3 х - 8 = 0
2 2х+1 – 5 * 2х - 88 = 0
4 группа: 3х = 5х
25х = 72х
3 * 22х + 6х - 2 * 32х = 0
В завершении этой части урока названы следующие способы решения показательных уравнений:
-
графический способ ( построение в одной системе координат графика показательной или логарифмической функции и графика функции, задающей правую часть уравнения; ответ – абсцисса точки пересечения графиков);
-
замена переменной и сведение к алгебраическому уравнению;
-
способ разложения на множители (вынесение общего множителя за скобку);
-
для однородных уравнений – почленное деление на выражение, не равное нулю;
-
р
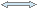 ешение простейших уравнений с использованием утверждения: а f (x) = a g (x) f(x) = g(x) (решение простейшего уравнения встечается почти во всех видах уравнений на заключительном этапе решения).
ешение простейших уравнений с использованием утверждения: а f (x) = a g (x) f(x) = g(x) (решение простейшего уравнения встечается почти во всех видах уравнений на заключительном этапе решения).
Решения уравнений сохраняются в течение урока на доске, учитель по необходимости корректирует образцы записи решения уравнений.
3. Формирование умений и навыков решения уравнений.
Самостоятельная работа учащихся по решению уравнений представленными выше способами.
Уравнения для самостоятельного решения:
-
22x – 6 * 2x + 8 = 0
-
9х + 8 * 3х = 9
-
52x + 1 – 26 * 5 x + 5 = 0
-
3x =
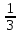 х2
х2 -
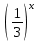 = x + 11
= x + 11 -
2х – 2х-2 = 3
-
3х+2 + 3х = 810
-
5х -
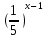 = 4
= 4 -
64 * 82х + х * 82х = 0
-
7 * 5х = 5 * 7х
-
3 * 22х + 6х – 2 * 32х = 0
-
3 * 4х – 5 * 6х + 2 * 9х = 0
4. Рефлексия. Самооценка.
Учитель: Вот и подходит к концу сегодняшний урок. Что нового вы на этом уроке узнали?
Учащиеся: Узнали больше о показательных уравнениях. Убедились в том, что новые уравнения можно решать «старыми» способами.
Учитель: И в заключении каждому предлагается оценить результат своей работы на уроке. Заполните, пожалуйста, итоговую таблицу.
| Знаю | Решаю по образцу | Решаю без образца | |
| Определение показательного уравнения | | ||
| Простейшие показат. уравнения | | ||
| Графический способ | |||
| Разложение на множители | |||
| Замена переменной | |||
| Почленное деление для однородных показат. урав. |
-
Домашнее задание.
Учитель: Предлагаемое сегодня домашнее задание будет у каждого из вас свое. Каждый определит его сам: параграф 46 задачника содержит множество показательных уравнений, решаемых различными способами, в том числе и такими, о которых (применительно к показательным уравнениям) не было сказано на уроке. Очень бы хотелось в домашней работе увидеть уравнения, решаемые различными способами.
Урок окончен, всем спасибо за работу.
Используемая литература:
-
А.Г. Мордкович. Алгебра и начала анализа (в 2-х частях)
-
Открытый банк задач ЕГЭ по математике
-
М.А. Попов. Контрольные и самостоятельные работы по алгебре и началам анализа: 11 класс: к учебнику А.Г. Мордковича
-
А.Г. Мордкович, Е.Е. Тульчинская. Алгебра и начала анализа. 10 – 11 классы. Контрольные работы для общеобразовательных учреждений.
-
В.С. Крамор Повторяем и систематизируем школьный курс алгебры и начал анализа. М., Просвещение, 1990.
Здесь представлен конспект к уроку на тему «Решение показательных уравнений», который Вы можете бесплатно скачать на нашем сайте. Предмет конспекта: Алгебра (11 класс). Также здесь Вы можете найти дополнительные учебные материалы и презентации по данной теме, используя которые, Вы сможете еще больше заинтересовать аудиторию и преподнести еще больше полезной информации.

