Организация повторения по алгебре в 11 профильном классе для подготовки к решению заданий С3 в ЕГЭ
Муниципальное бюджетное общеобразовательное учреждение лицей № 6
городского округа Тольятти
Методическая разработка
«Организация повторения по алгебре
в 11 профильном классе
для подготовки к решению заданий С3 в ЕГЭ»
Подготовила
Овчинникова Наталья Александровна,
учитель математики высшей категории
МБУ лицея №6 г. о. Тольятти
Тольятти
2014
Тема «Организация повторения по алгебре в 11 профильном классе
для подготовки к решению заданий С3 в ЕГЭ»
Система уроков повторения по теме «Решение неравенств функционально – графическим методом» содержит: примерное планирование учебного времени; краткий анализ знаний и умений учащихся, полученных на уроках повторения по выбранной теме; план-конспект одного из уроков; проверочную работу (в одном варианте).
-
Примерное планирование учебного времени
-
Использование области определения функций.(1 час)
-
Использование монотонности функций.(1 час)
-
Использование ограниченности функций. (2 часа)
-
Метод интервалов для непрерывных функций. (2 часа)
-
Использование графиков функций. (1 час)
-
Проверочная работа. (1 час)
-
Краткий анализ и умений знаний учащихся, полученных на уроках повторения по выбранной теме.
В результате повторения данной темы учащиеся должны иметь четкое представление о возможностях функционально-графического подхода к решению неравенств.
Уметь:
-
решать неравенства с использованием области определения входящих в них функций, свойства монотонности функций;
-
использовать при решении неравенств свойство ограниченности функции на некотором множестве, уметь находить наибольшее и наименьшее значение функций или их композиций на заданном множестве;
-
применять метод интервалов при решении неравенств, содержащих различные функции, а также при решении трансцендентных неравенств, используя идею рационализации неравенств;
-
уметь при решении неравенств рассмотреть эскиз графиков их правой и левой частей в одной и той же системе координат. Тогда этот эскиз графиков поможет выяснить, на какие множества надо разбить числовую ось, чтобы на каждом из них решение неравенства было очевидно;
-
использовать приобретённые знания и умения в практической деятельности при подготовке к ЕГЭ.
-
План – конспект урока по теме:
«Метод интервалов для непрерывных функций» (2 часа)
Цели урока:
Обучающие:
-
обобщить ранее изученный материал о решении неравенств методом
интервалов; возможность применения метода интервалов для
решения неравенств различного типа; -
выработка умений и навыков в решении неравенств различного типа
методом интервалов; -
решение трансцендентных неравенств, с использованием метода рационализации.
Развивающие:
-
повысить интерес учащихся к нестандартным задачам, сформировать у них
положительный мотив учения; -
развитие у учащихся логического мышления в процессе поиска рациональных методов и алгоритмов решения;
Воспитательные:
-
формирование нравственных качеств, аккуратности, дисциплинированности, чувства собственного достоинства, ответственного отношения к достижению цели;
-
развитие культуры научных и учебных взаимоотношений между учениками и между учениками и учителем; воспитание навыков совместного решения задач.
Тип урока: урок обобщения и систематизации знаний.
План урока:
-
Организационный момент.
-
Повторение и актуализация опорных знаний.
-
Решение неравенств методом интервалов.
-
Подведение итогов. Задание на дом.
Ход урока:
1. Организационный момент.
2. Повторение и актуализация опорных знаний.
Обобщенный метод интервалов.
-
Применимость метода интервалов не ограничивается решением рациональных неравенств.
-
Применяя метод интервалов к решению иррациональных, трансцендентных, комбинированных неравенств, говорим об обобщенном методе интервалов.
Алгоритм обобщенного метода интервалов:
-
Привести неравенство к виду
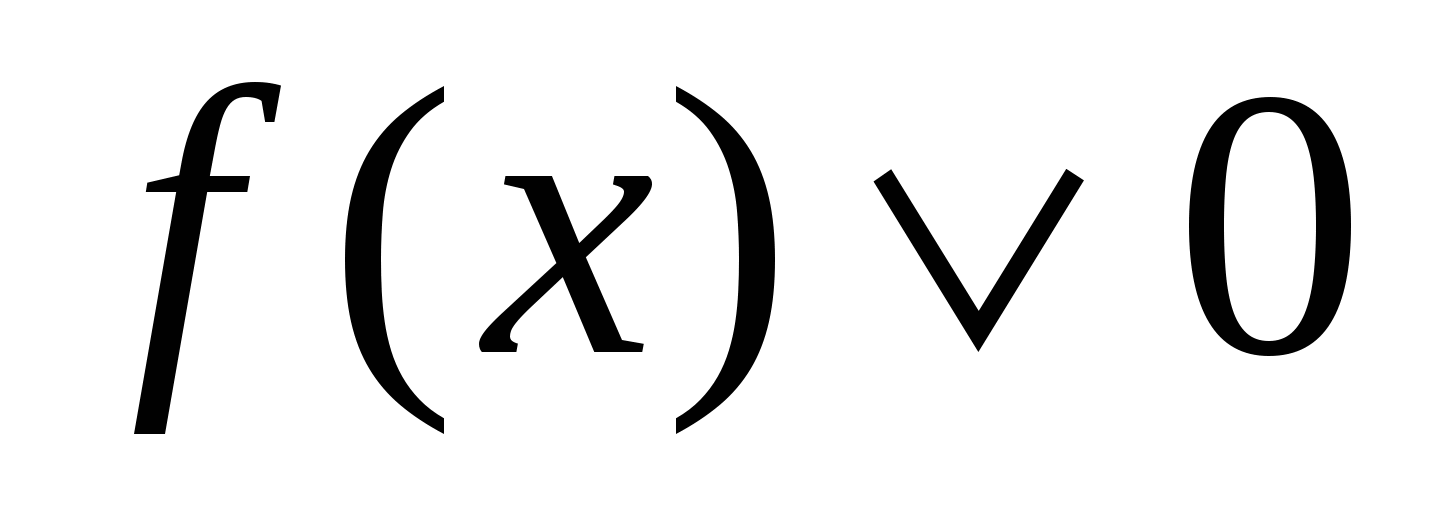 . Рассмотреть функцию
. Рассмотреть функцию 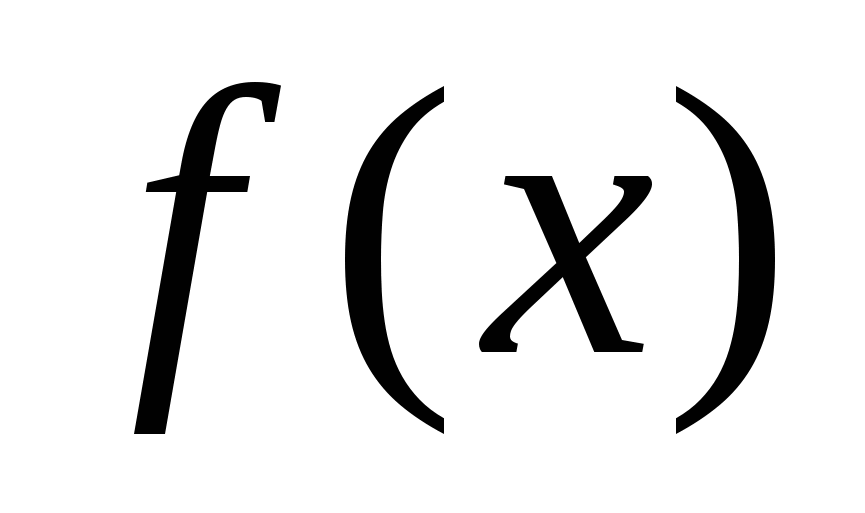 .
. -
Найти область определения функции
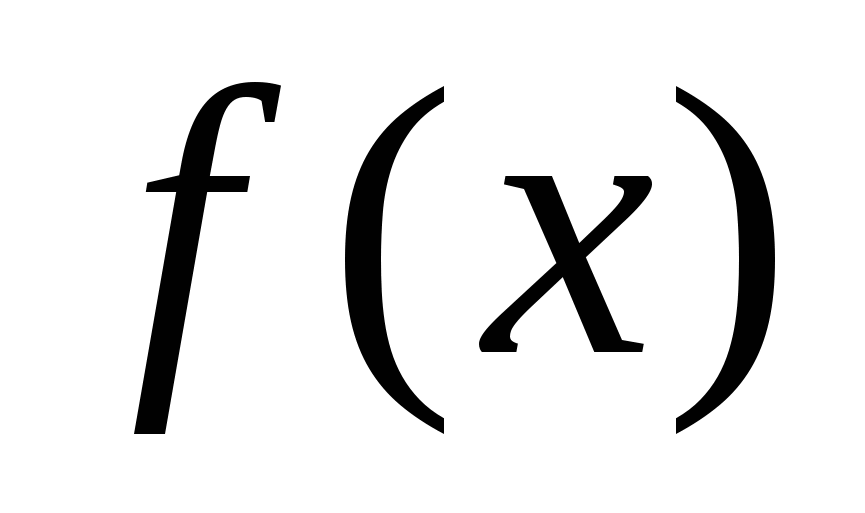 .
. -
Найти нули функции
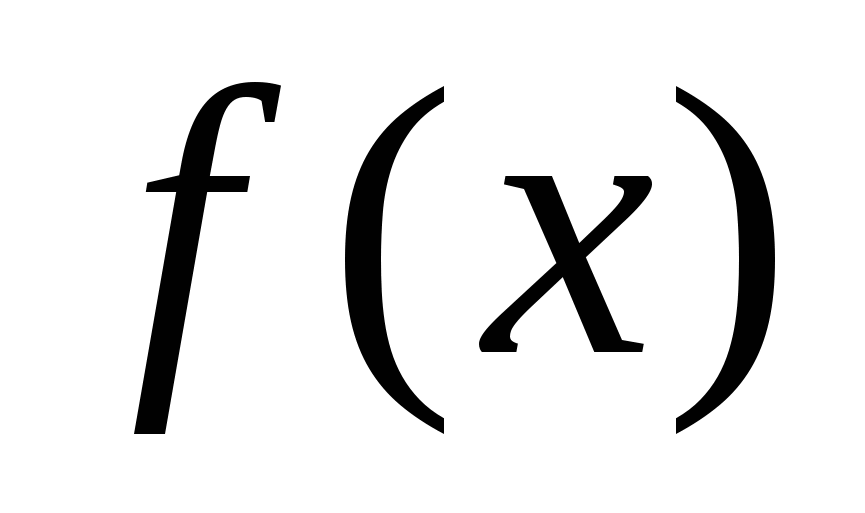 , решив уравнение
, решив уравнение 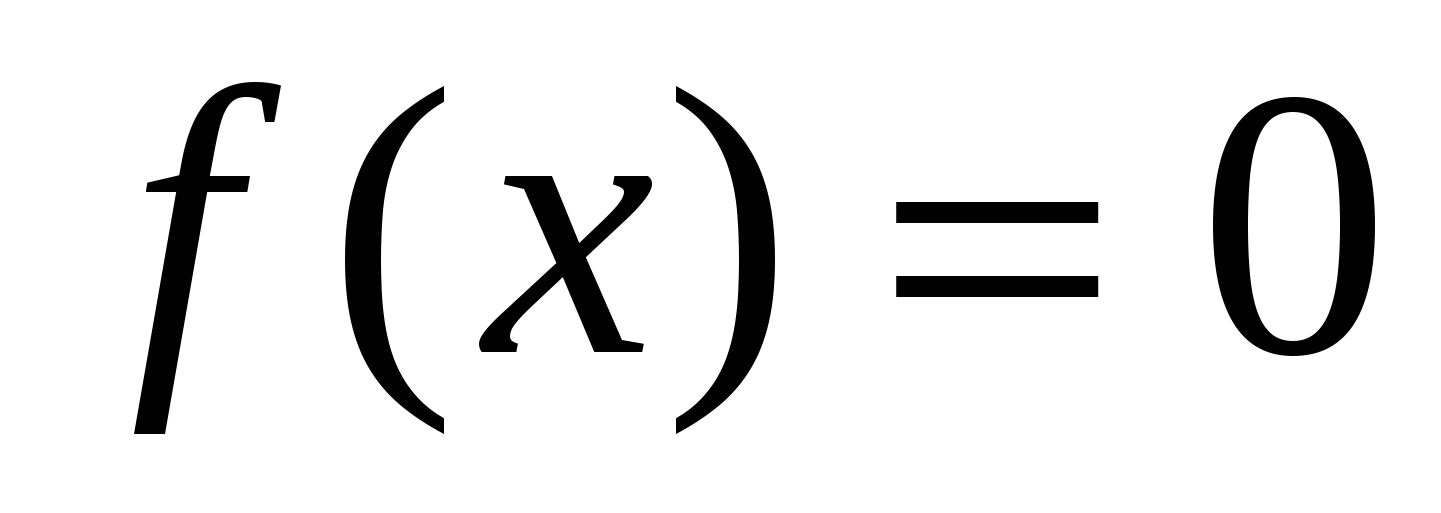
-
Изобразить на числовой прямой область определения и нули функции.
-
Определить знаки функции на промежутках, входящих в область определения функции.
-
Записать ответ, включив в него промежутки в соответствии со знаком неравенства (не забыть включить в ответ изолированные точки).
Метод рационализации.
-
Метод рационализации заключается в замене сложного выражения F(x) на более простое выражение G(x) (в конечном счете, рациональное), при которой неравенство
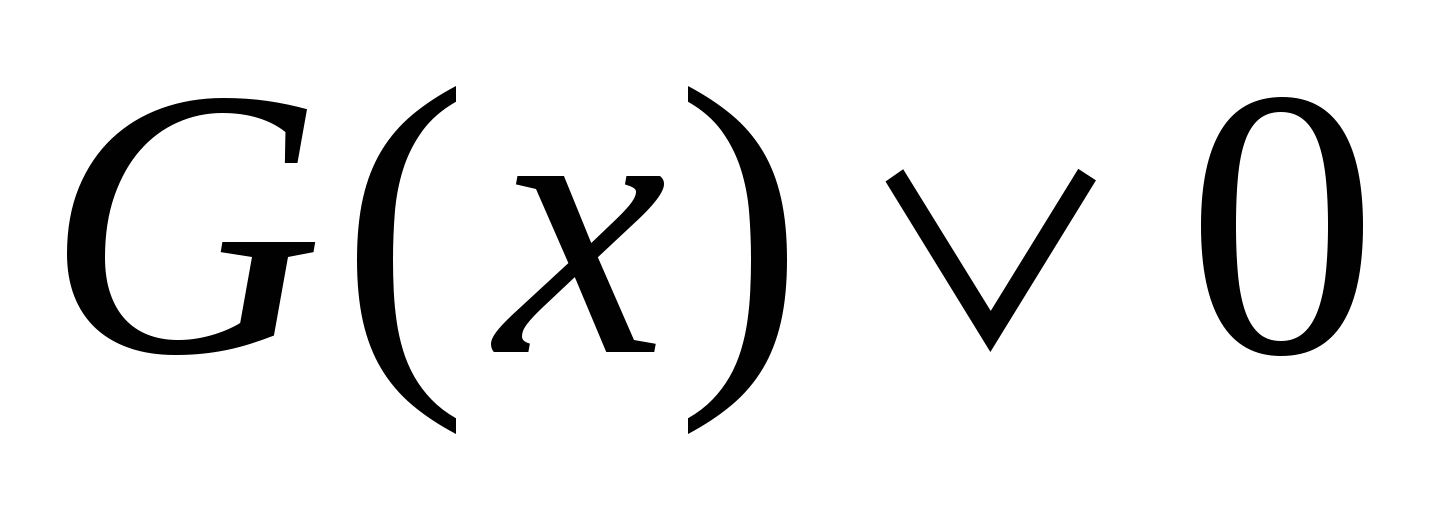 равносильно неравенству
равносильно неравенству 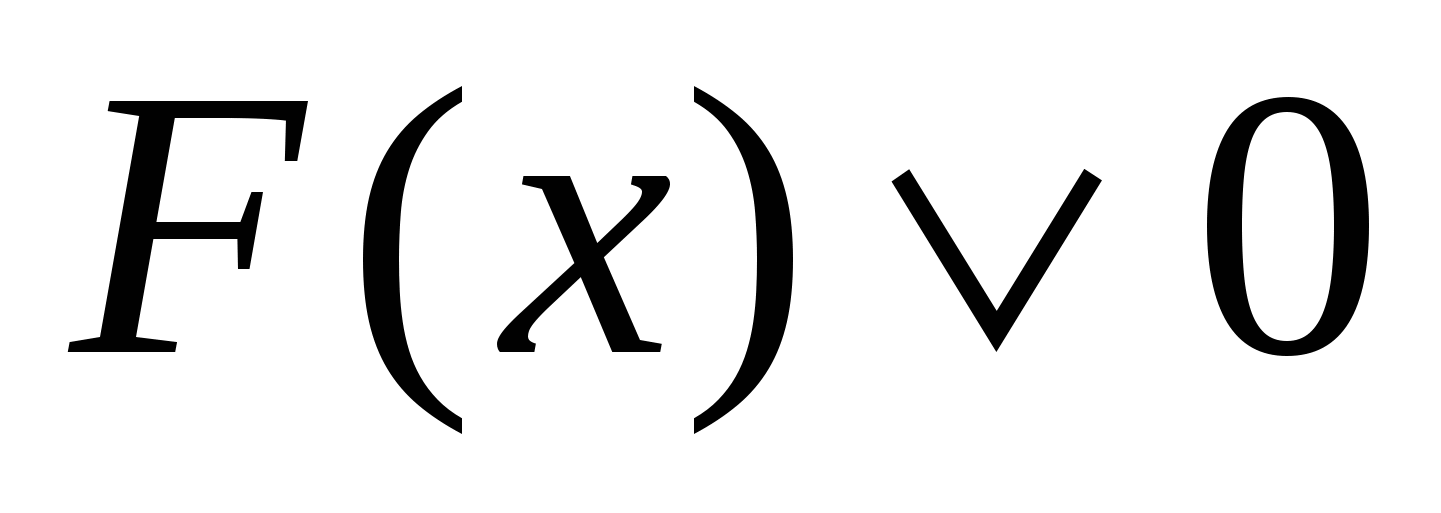 в области определения выражения F(x) (символ
в области определения выражения F(x) (символ заменяет один из знаков неравенств: >, ).
заменяет один из знаков неравенств: >, ). -
Выделим некоторые выражения F и соответствующие им рационализирующие выражения G.
-
Выражение F(x)
Выражение G(x)
loghf - loghg
(h – 1)(f – g)
logfh - loggh
(f – 1)(g – 1)(h – 1)(g – f)
hf - hg
(h – 1)(f – g)
fh - gh
(f – g)h
| f | - | g |
(f – g)(f + g)
loghf · logpg
(f – 1)(g – 1)(h – 1)(p – 1)
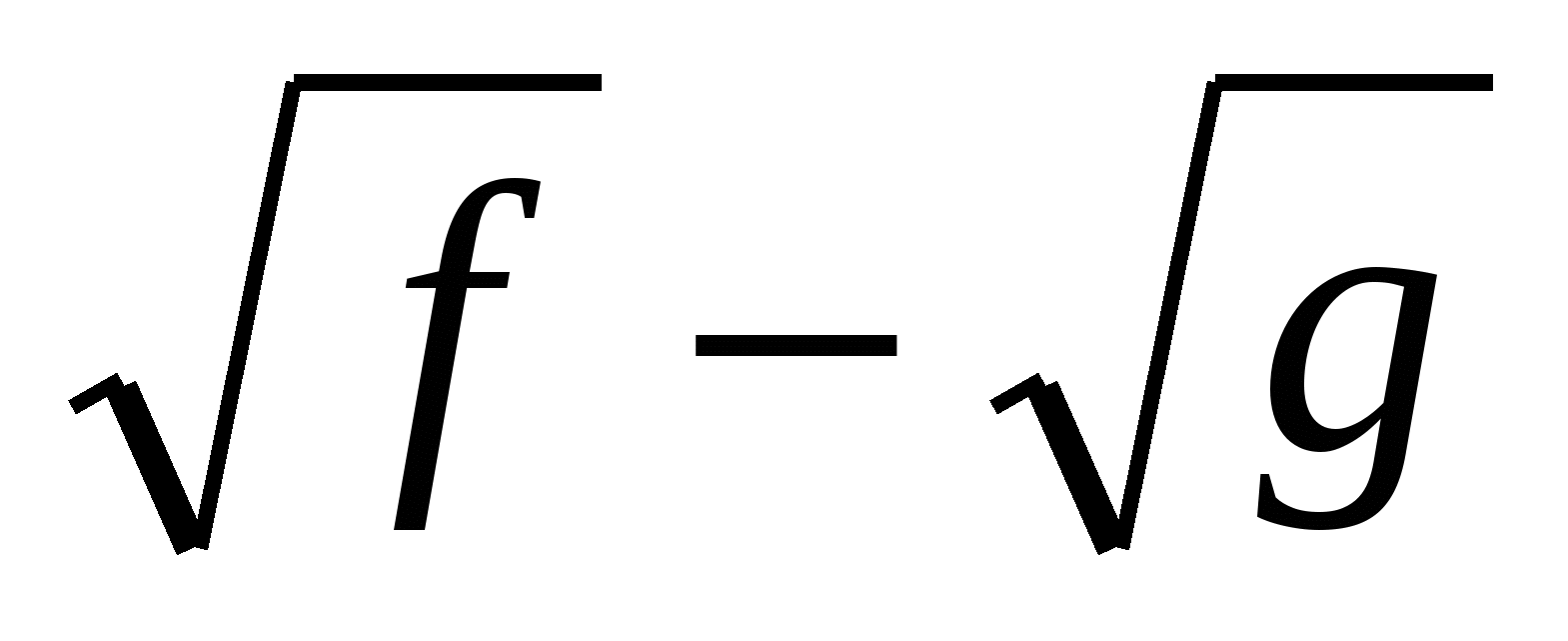
f- g
3. Решение неравенств методом интервалов
Каждое задание решает группа учащихся. Затем один из группы записывает решение на доске и поясняет его.
1). Решить неравенство ![]()
Используем метод интервалов для решения данного неравенства
-
Рассмотрим функцию
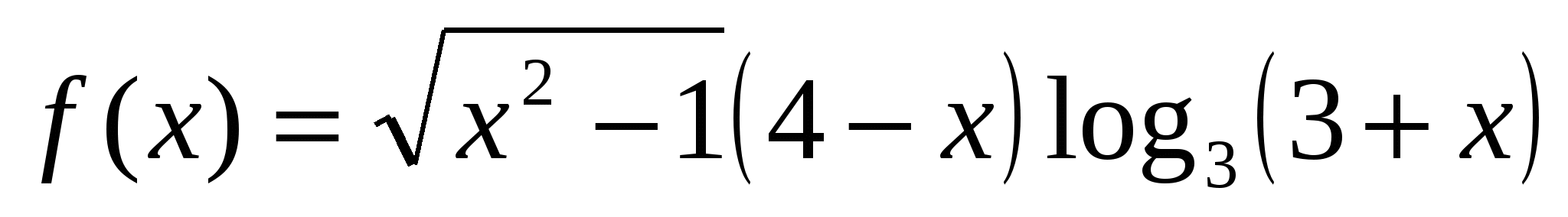
-
Найдем область определения функции
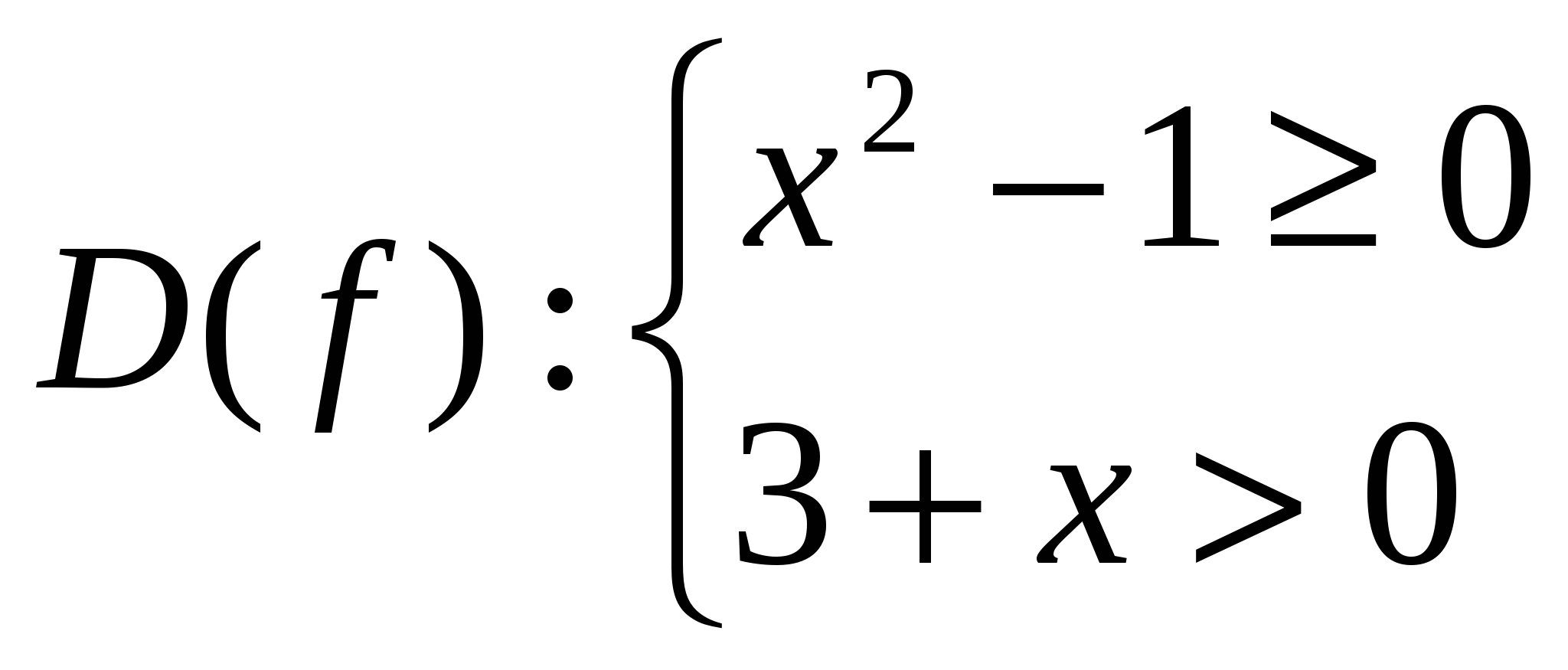
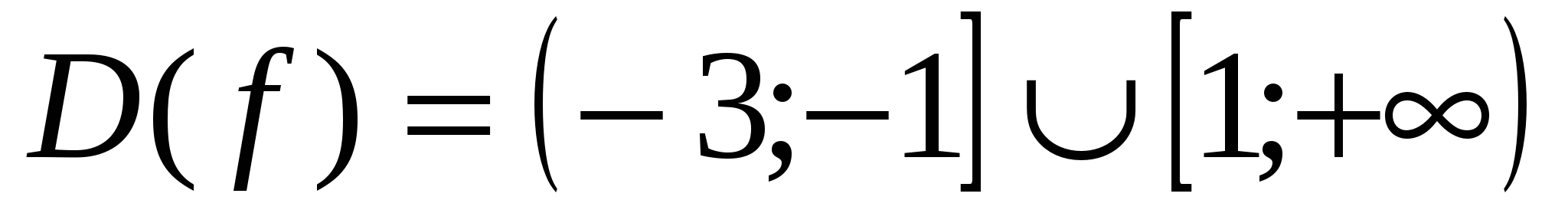
-
Найдем нули функции:
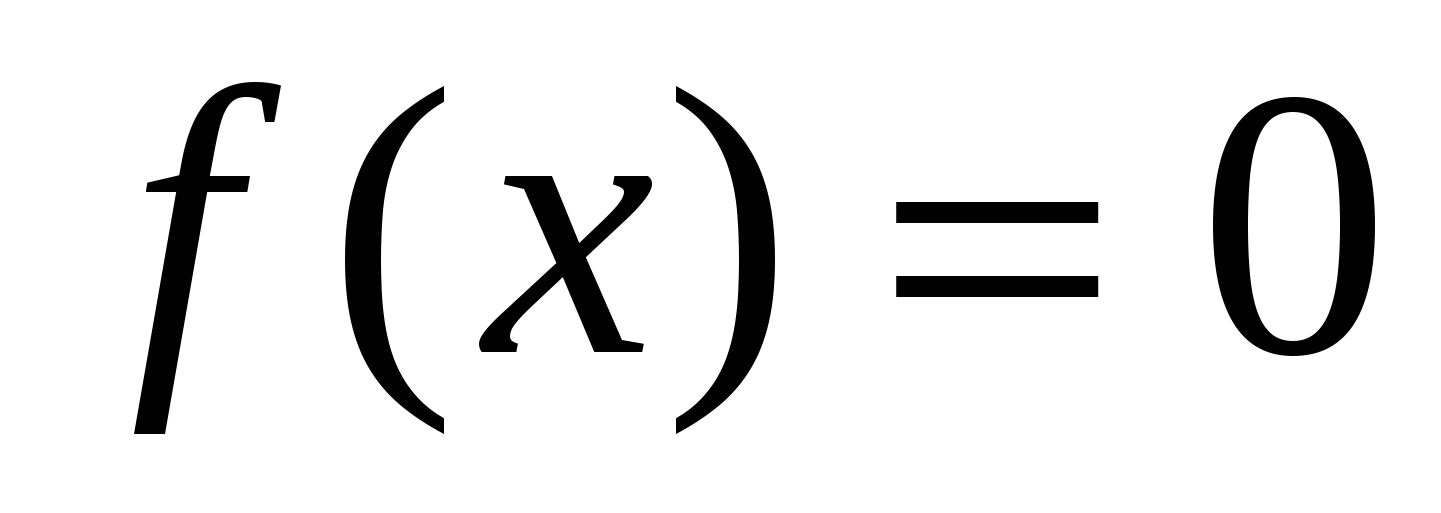
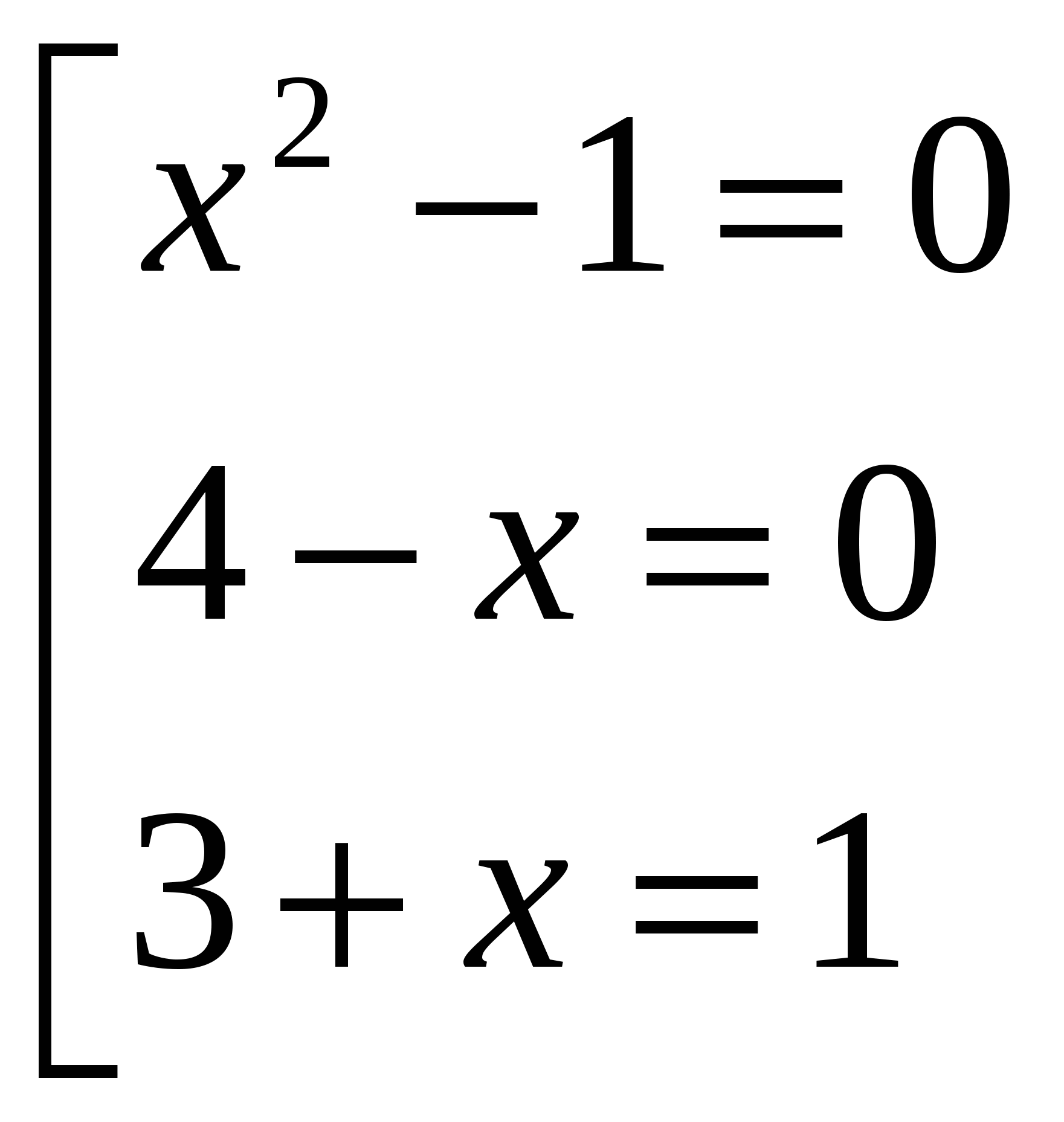
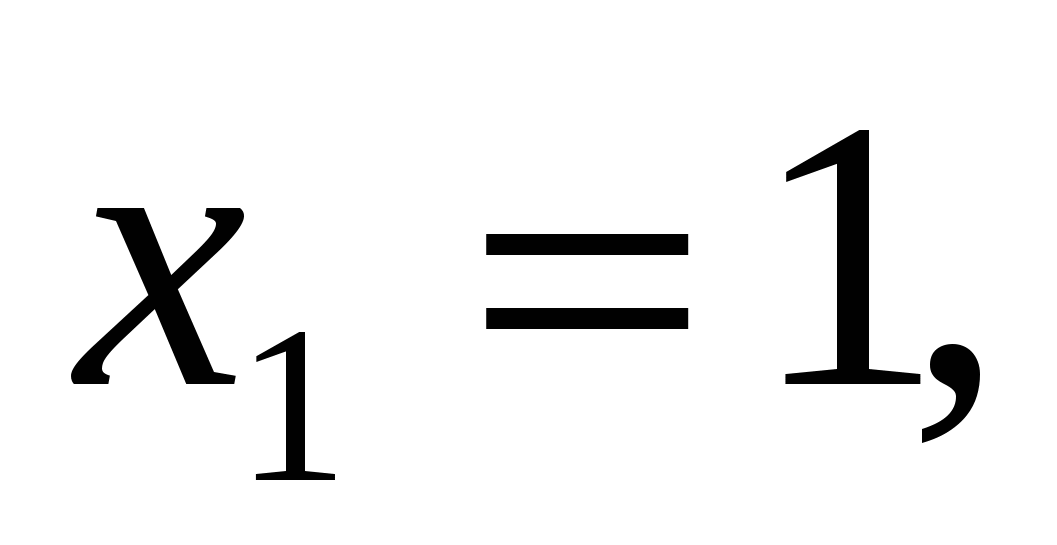
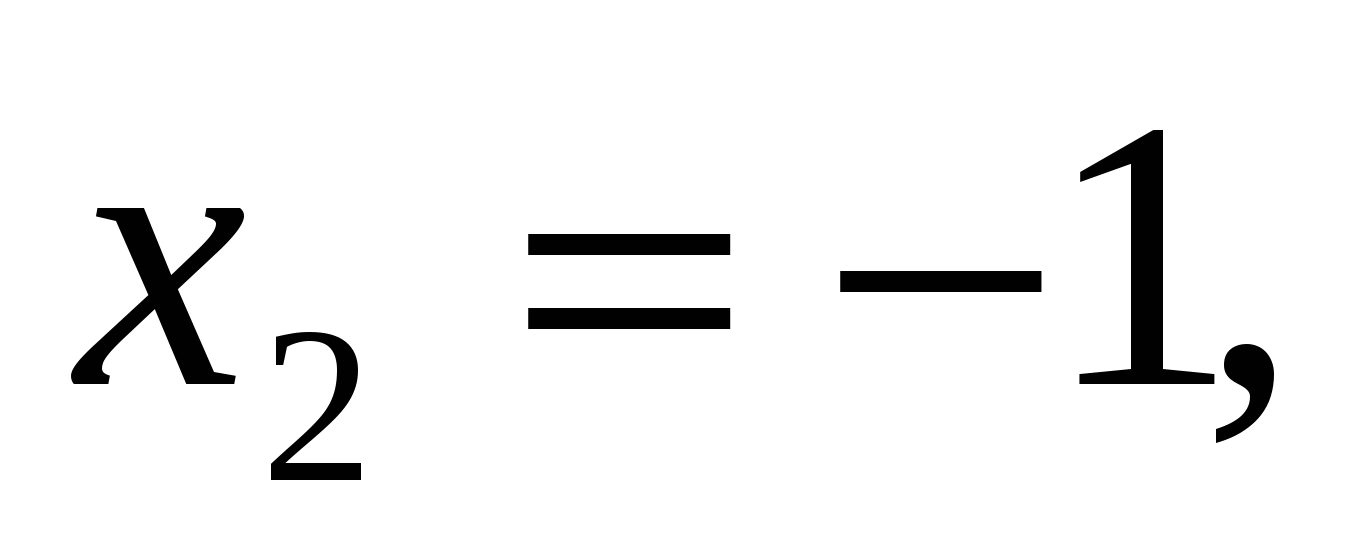
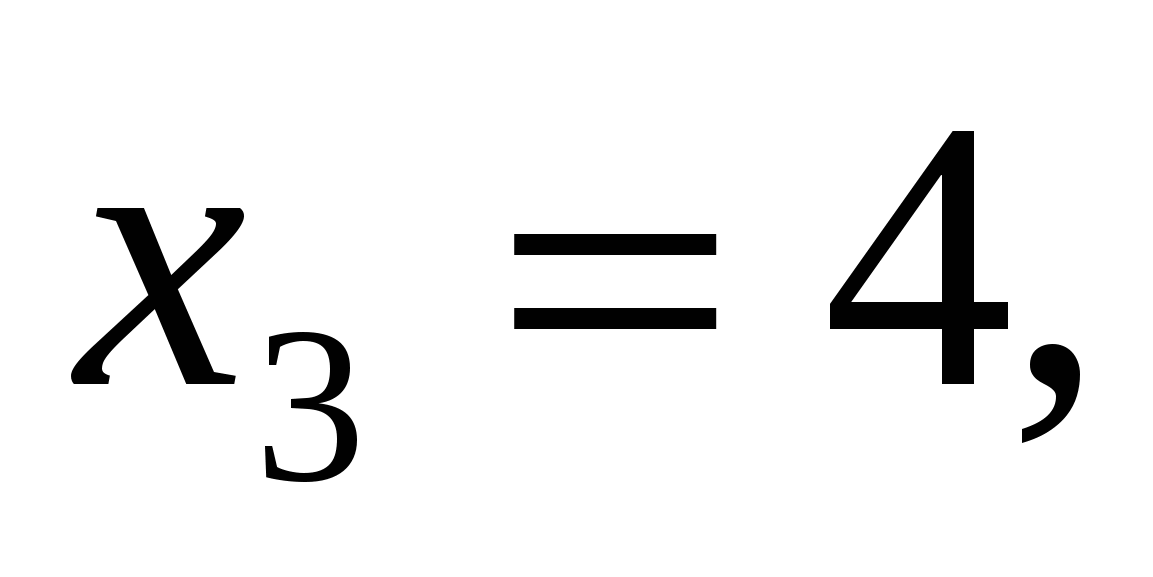
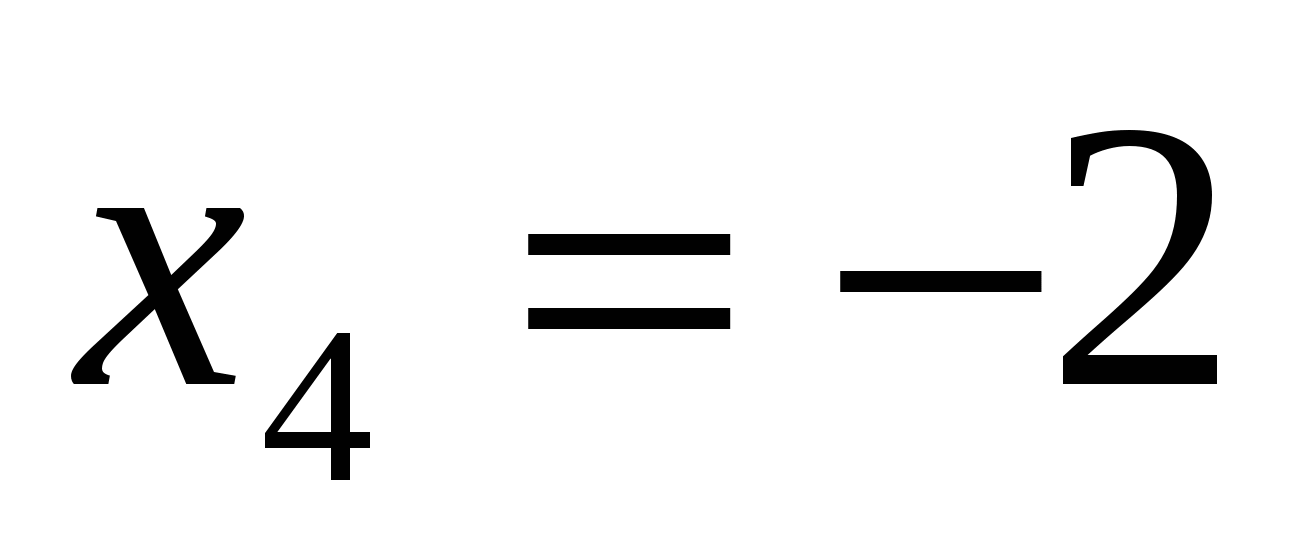
-
Определим знаки функции на каждом из промежутков
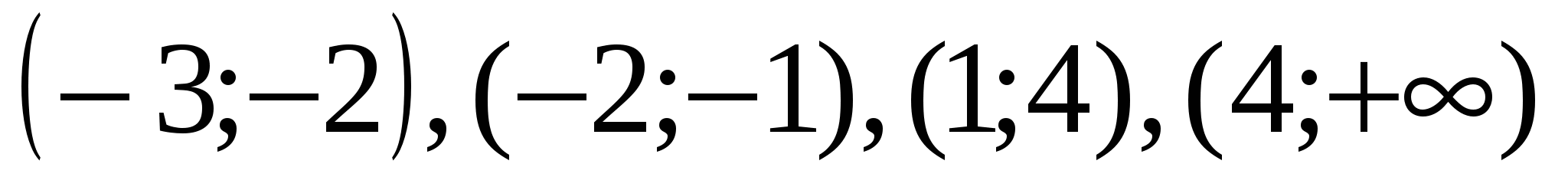

![]()
Следовательно, множеством решений исходного неравенства является объединение промежутков ![]()
Ответ: ![]()
2). Решить неравенство ![]()
Используем метод интервалов для решения данного неравенства
-
Рассмотрим функцию
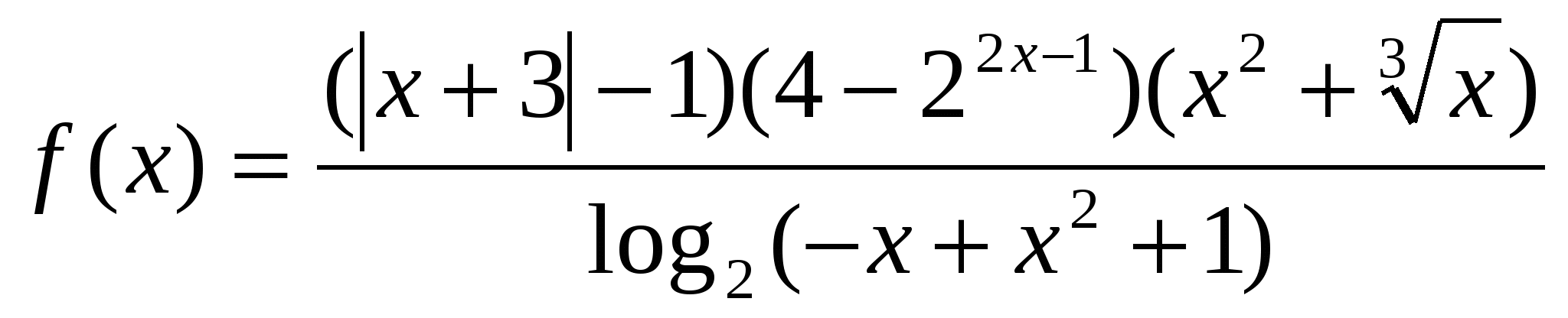
-
Найдем область определения функции
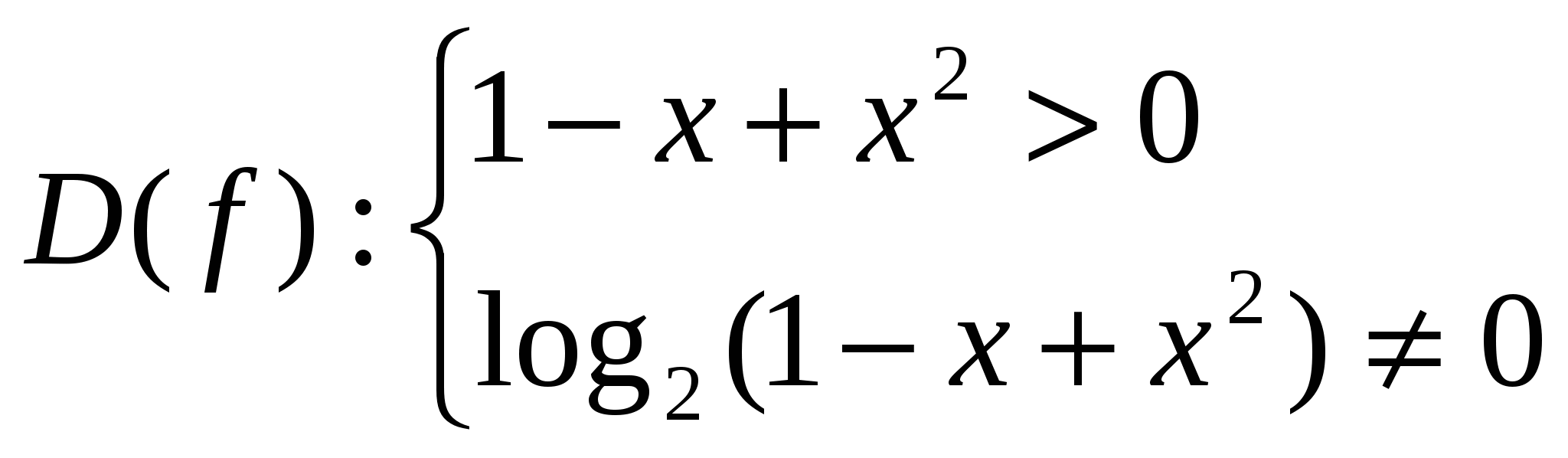
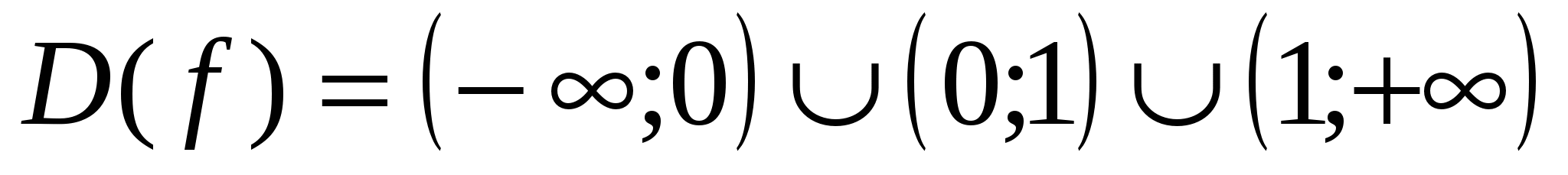
-
Найдем нули функции:
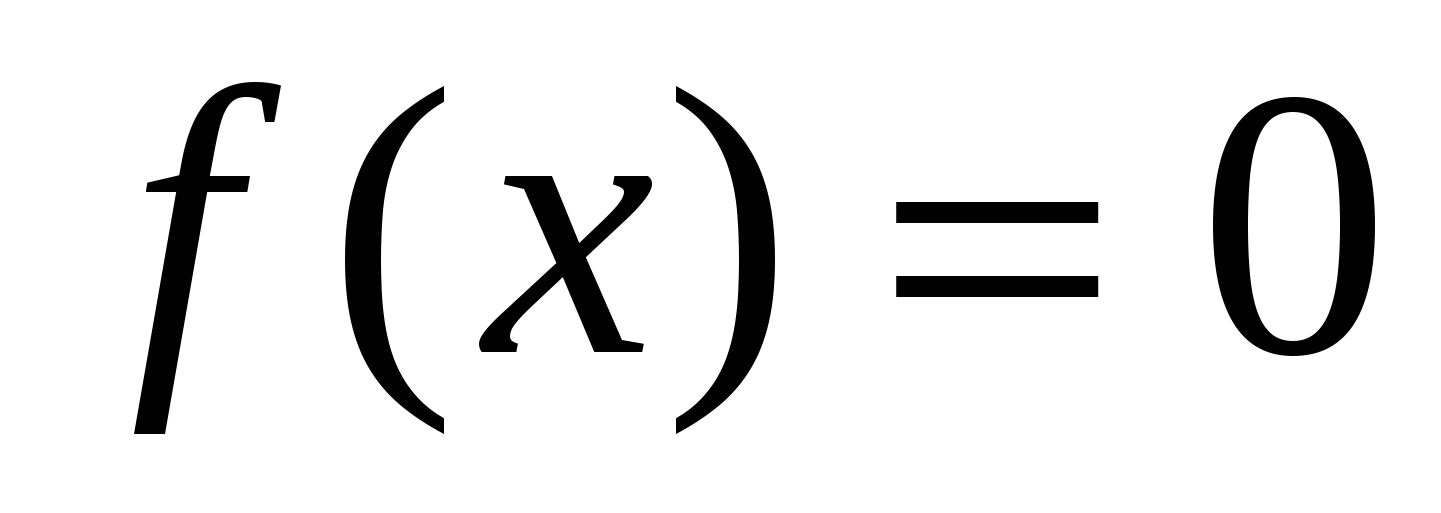
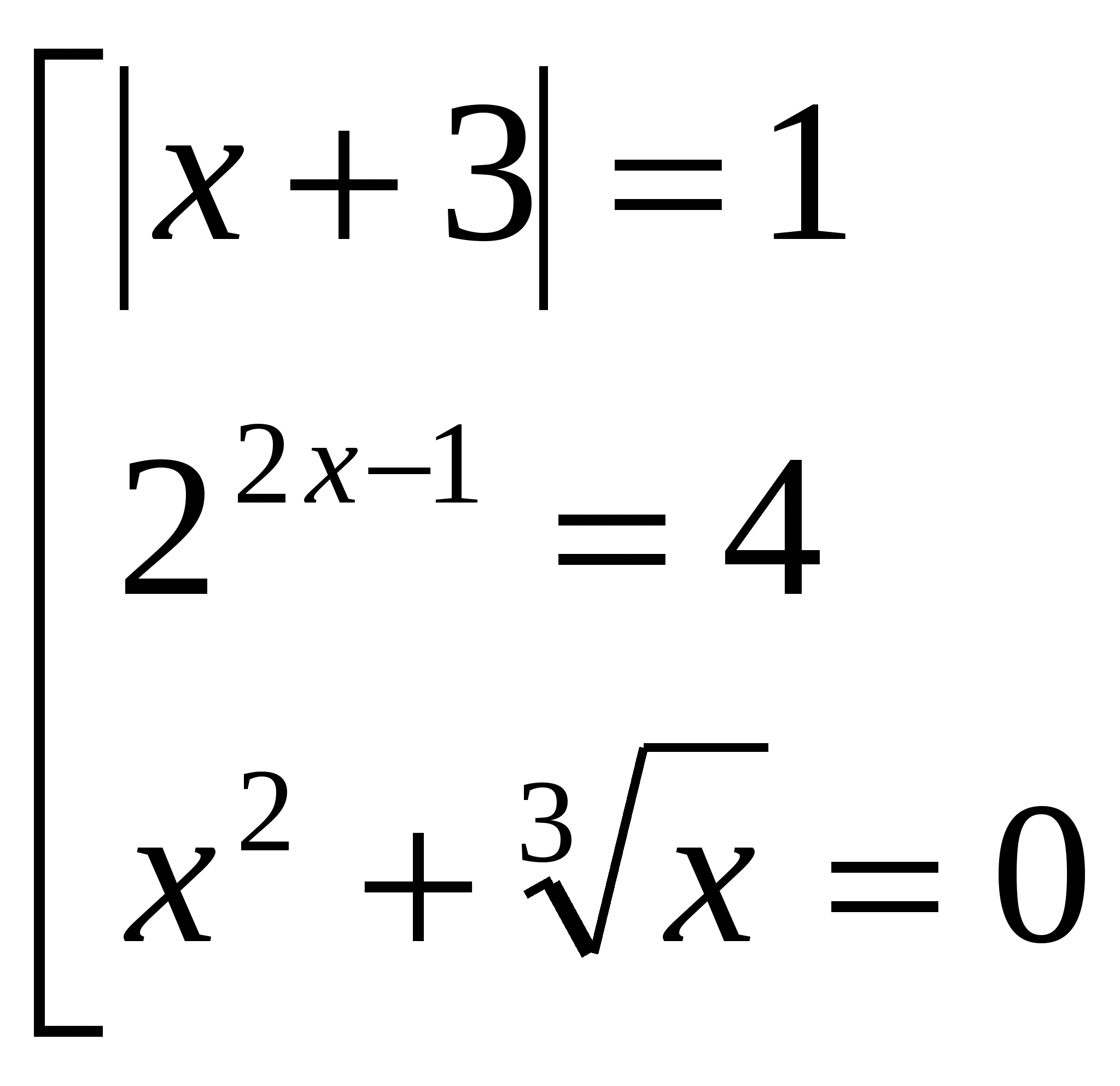 ,
, 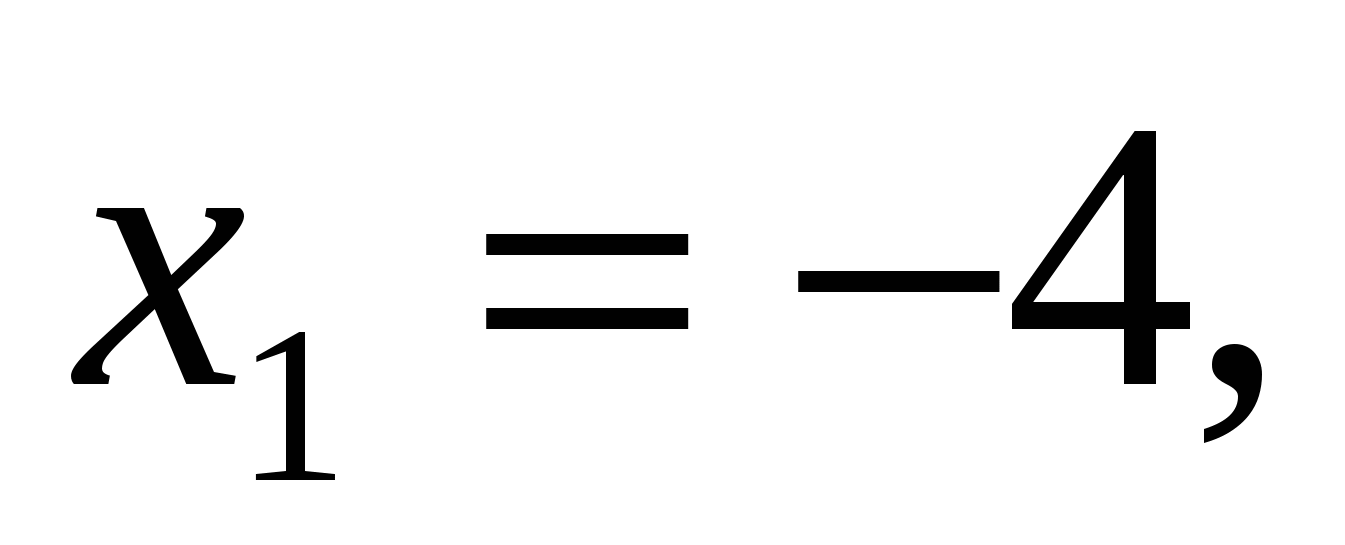
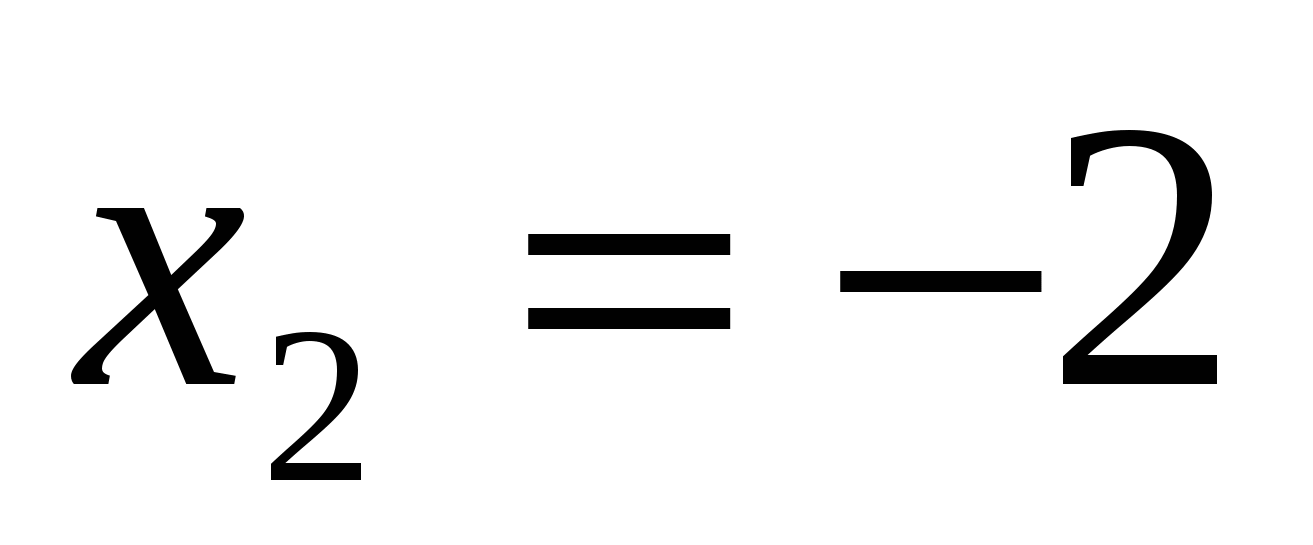
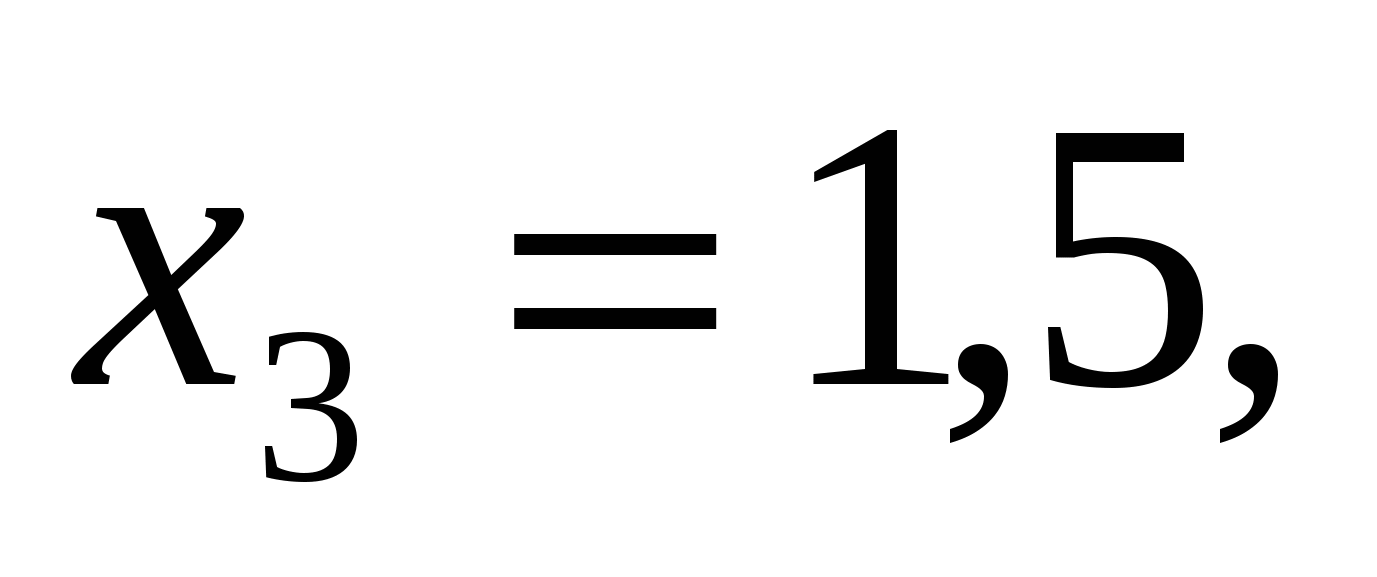
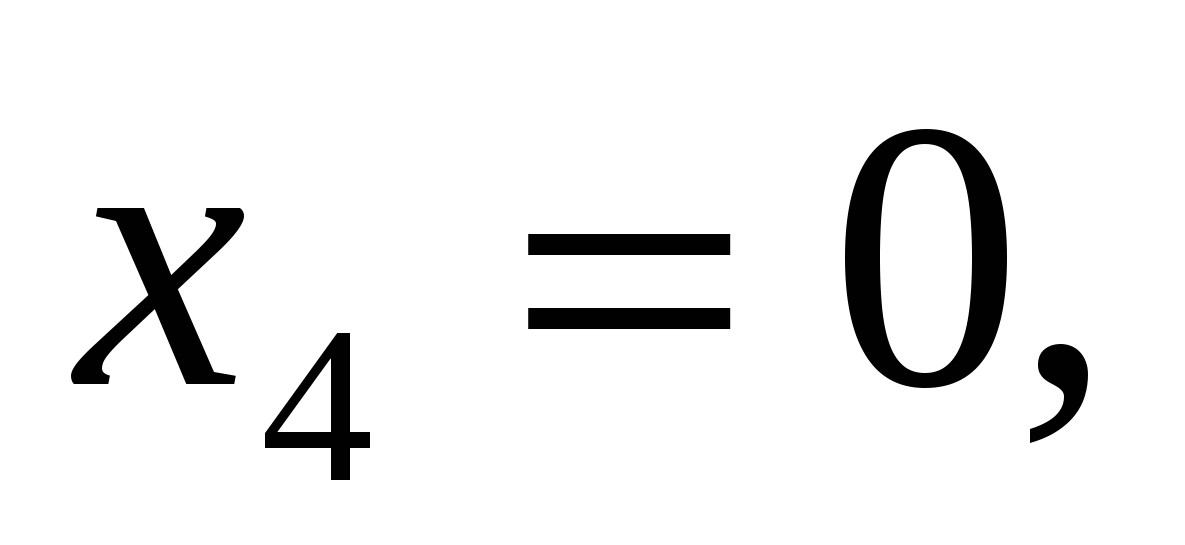
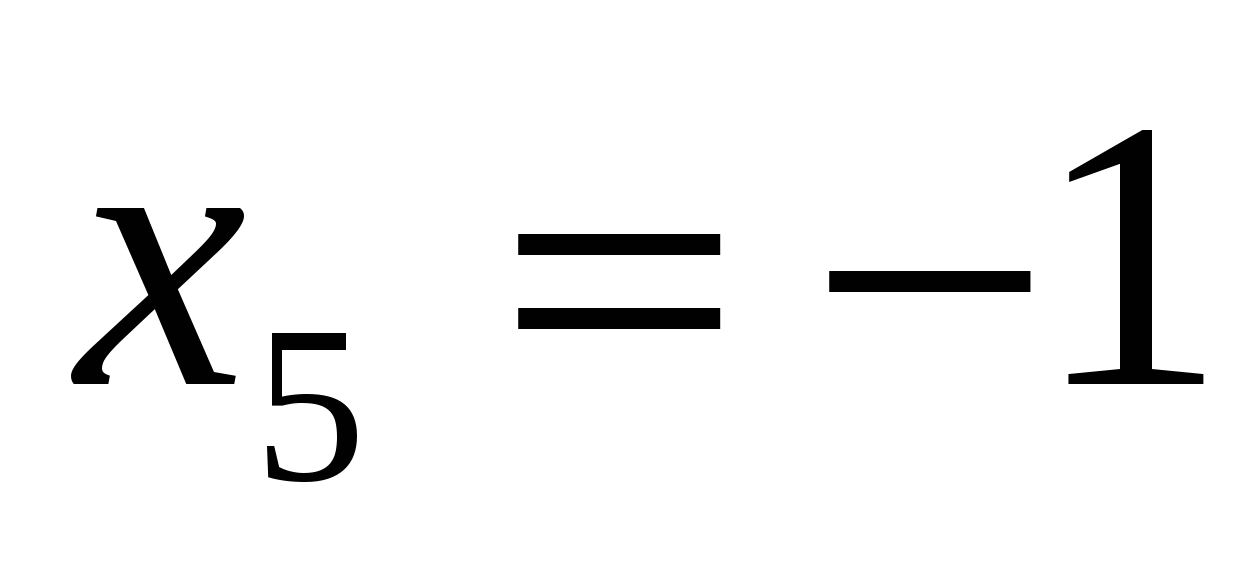
-
Определим знаки функции на каждом из промежутков
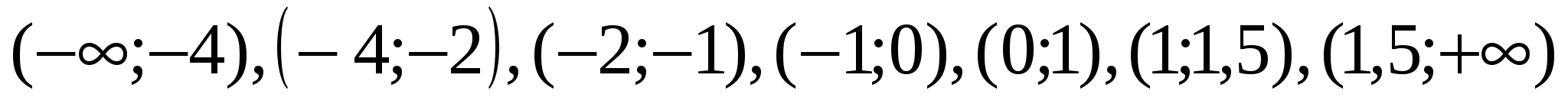

![]()
Следовательно, множеством решений исходного неравенства является объединение промежутков ![]()
Ответ: ![]()
3). Решить неравенство ![]()
Заменим данное неравенство равносильной системой, используя метод рационализации:
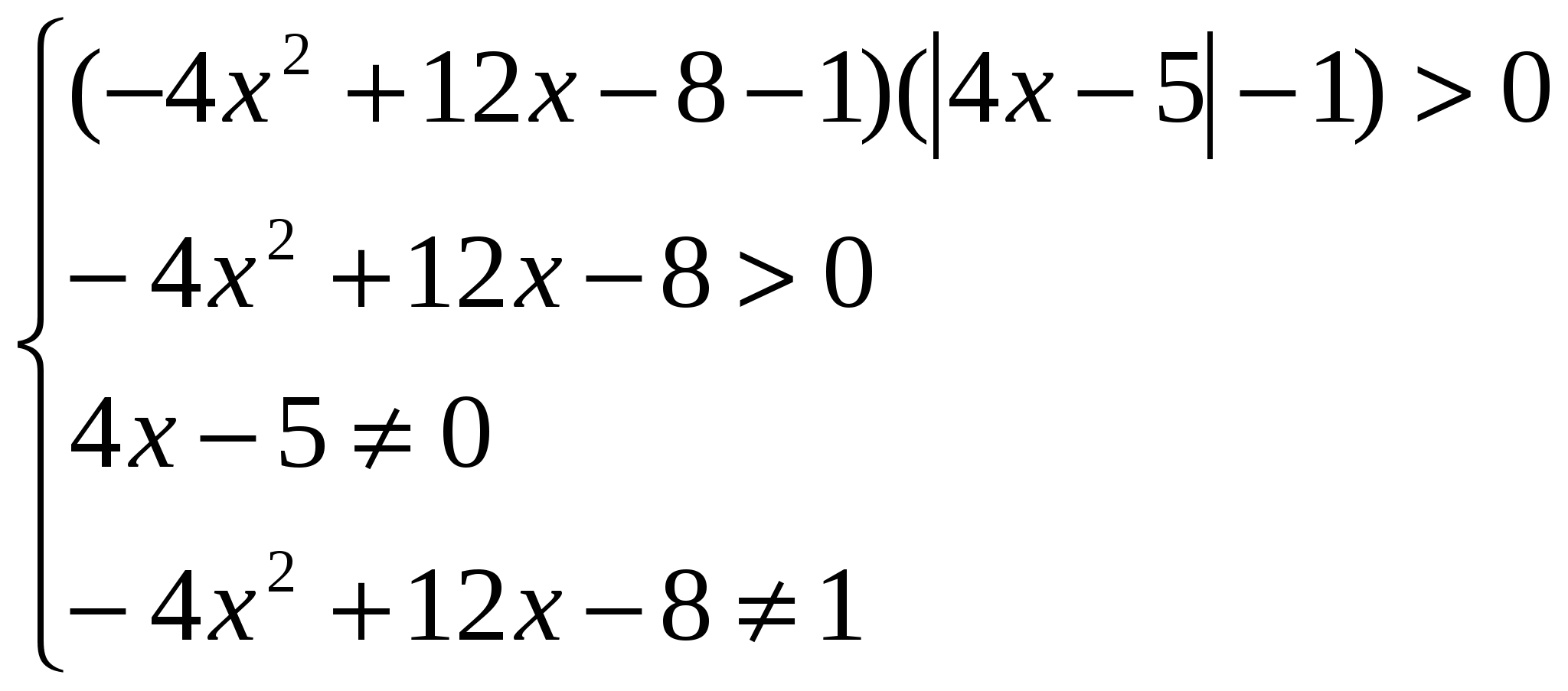
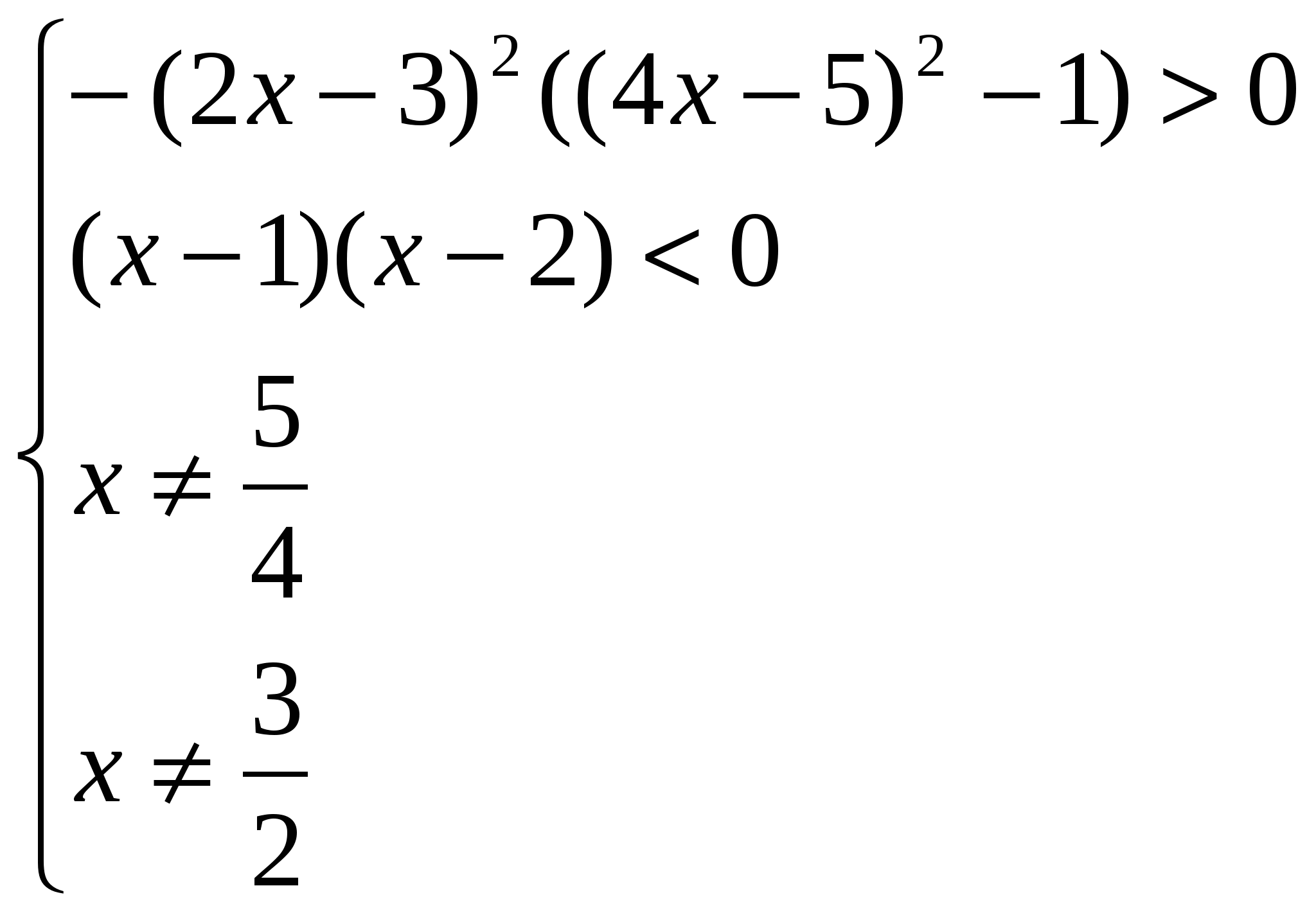
Окончательно получаем,что решением являются все х такие, что
![]()
![]() Ответ:
Ответ: ![]()
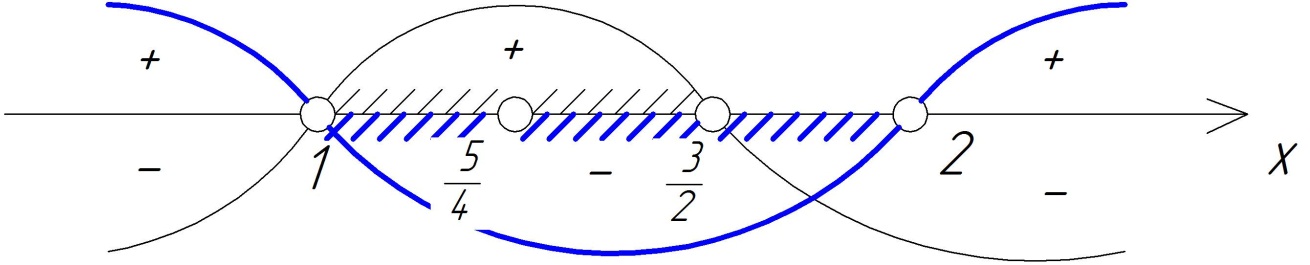
4). Решить неравенство 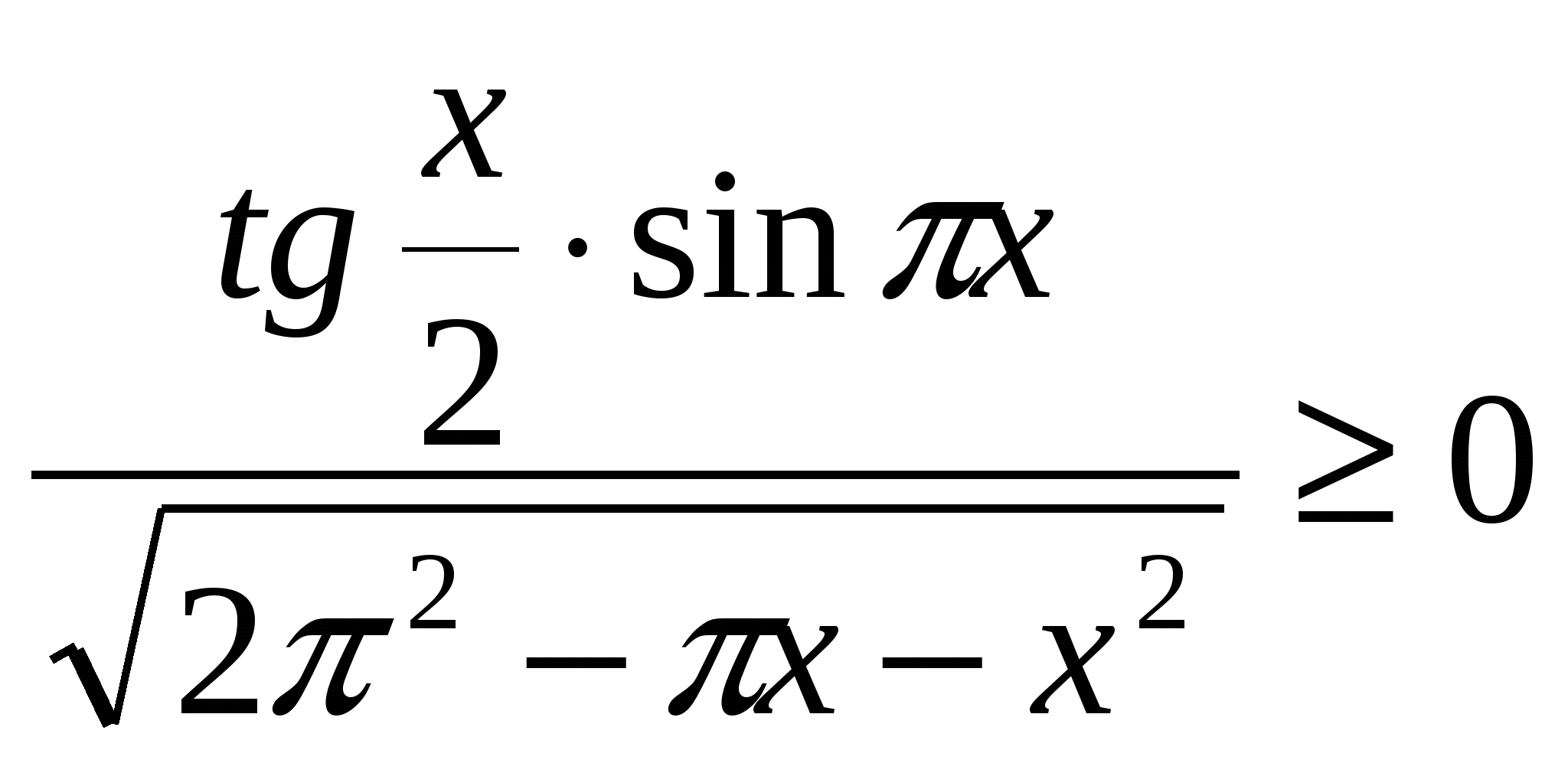
Воспользуемся методом интервалов:
-
Рассмотрим функцию
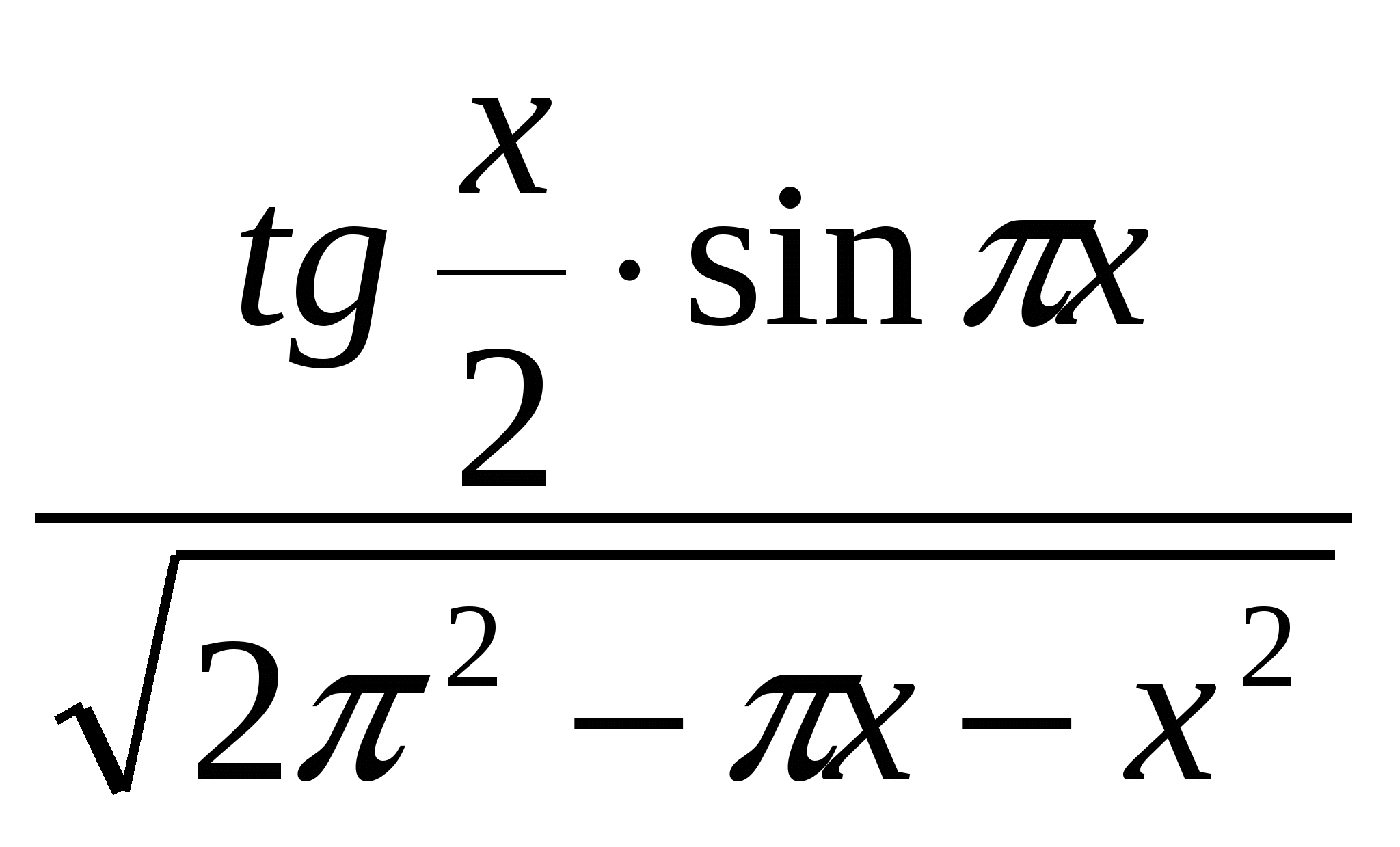
-
Найдем область определения функции
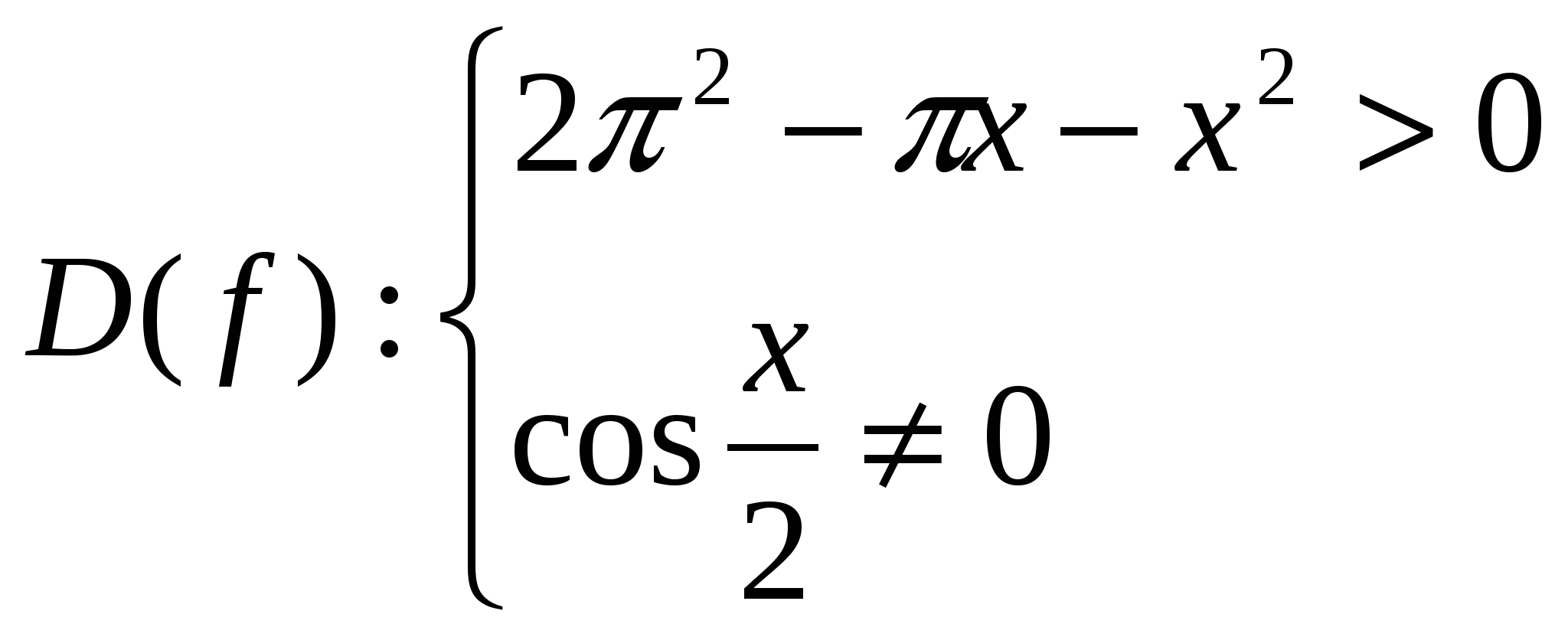
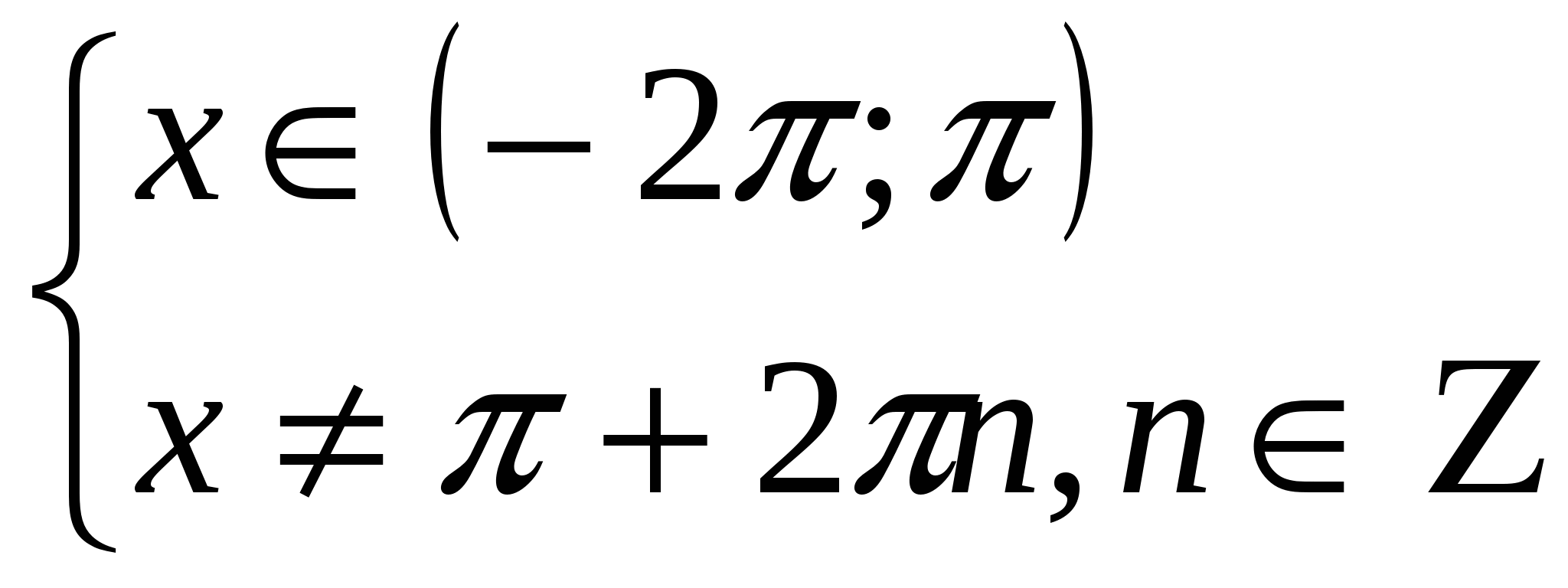
![]()
-
Найдем нули функции:
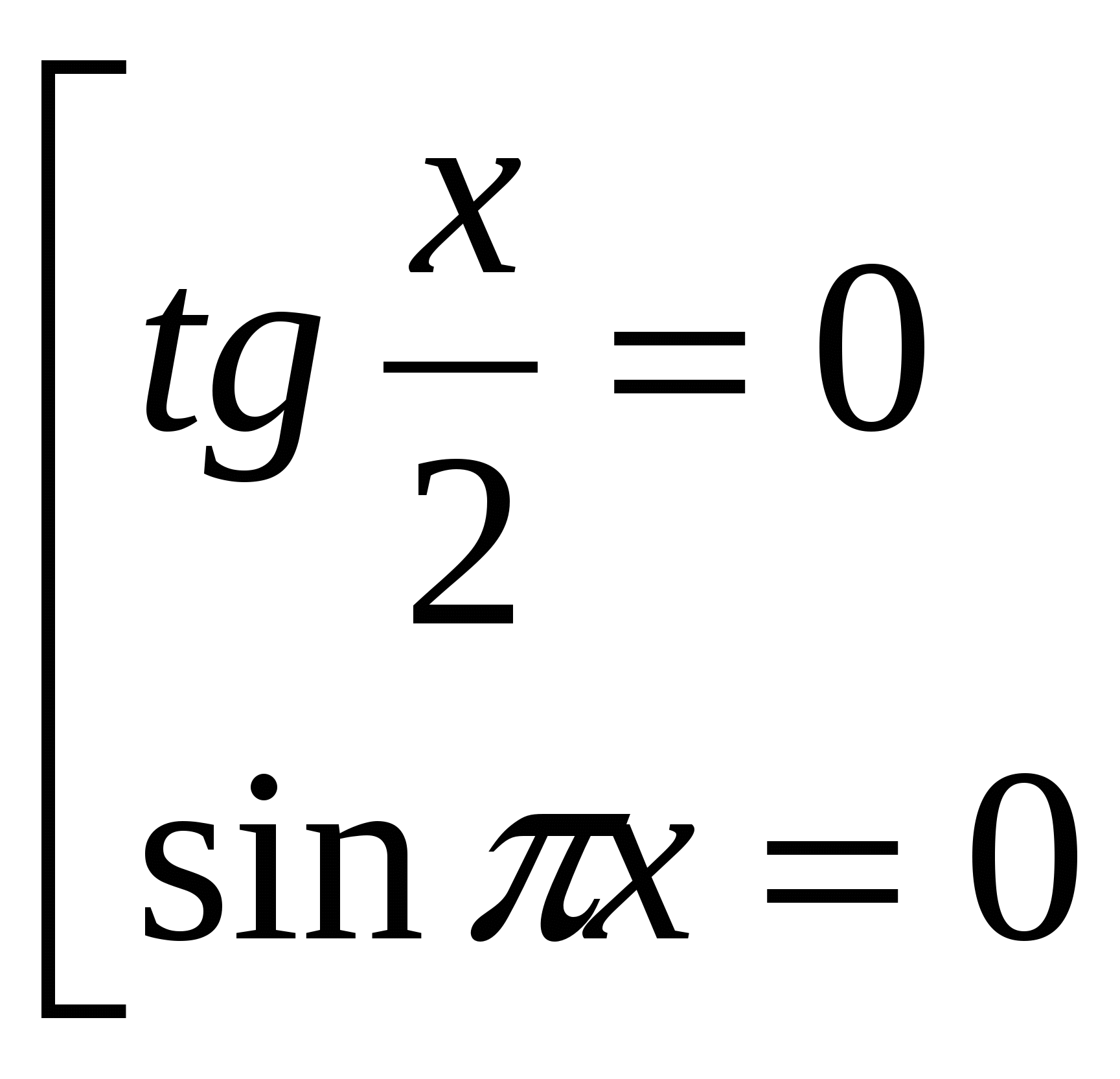
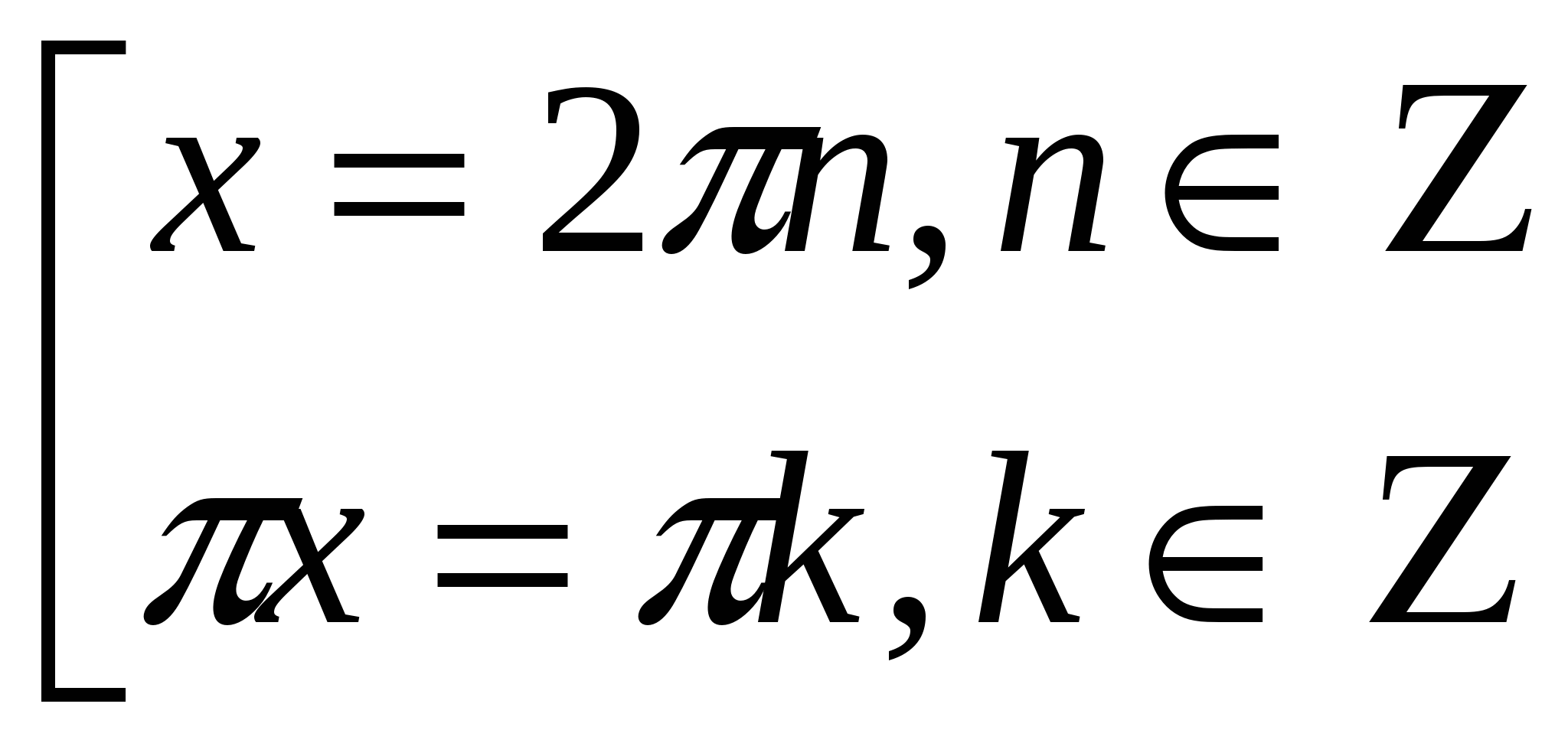
На промежутке ![]() лежат числа:
лежат числа:
![]()
-
Определим знаки функции на каждом из промежутков
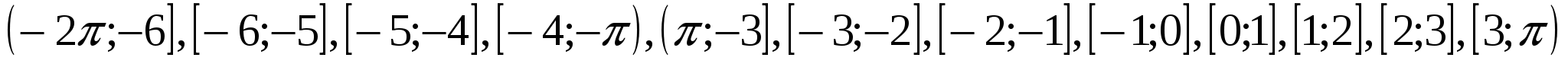

![]()
![]()
Множеством решений исходного неравенства является объединение промежутков
![]()
Ответ: ![]()
![]()
5). Решить неравенство![]()
![]()
Используем метод интервалов для решения данного неравенства
-
Рассмотрим функцию
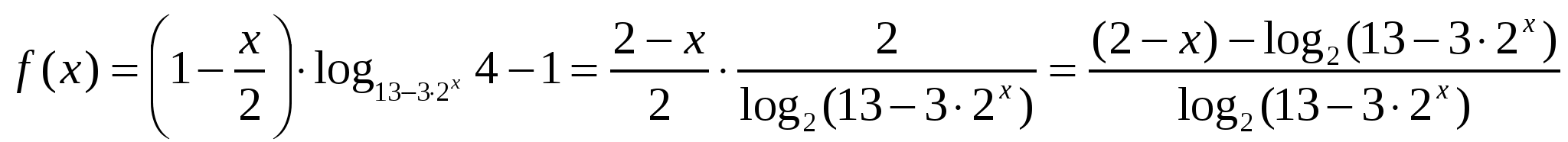
-
Найдем область определения функции
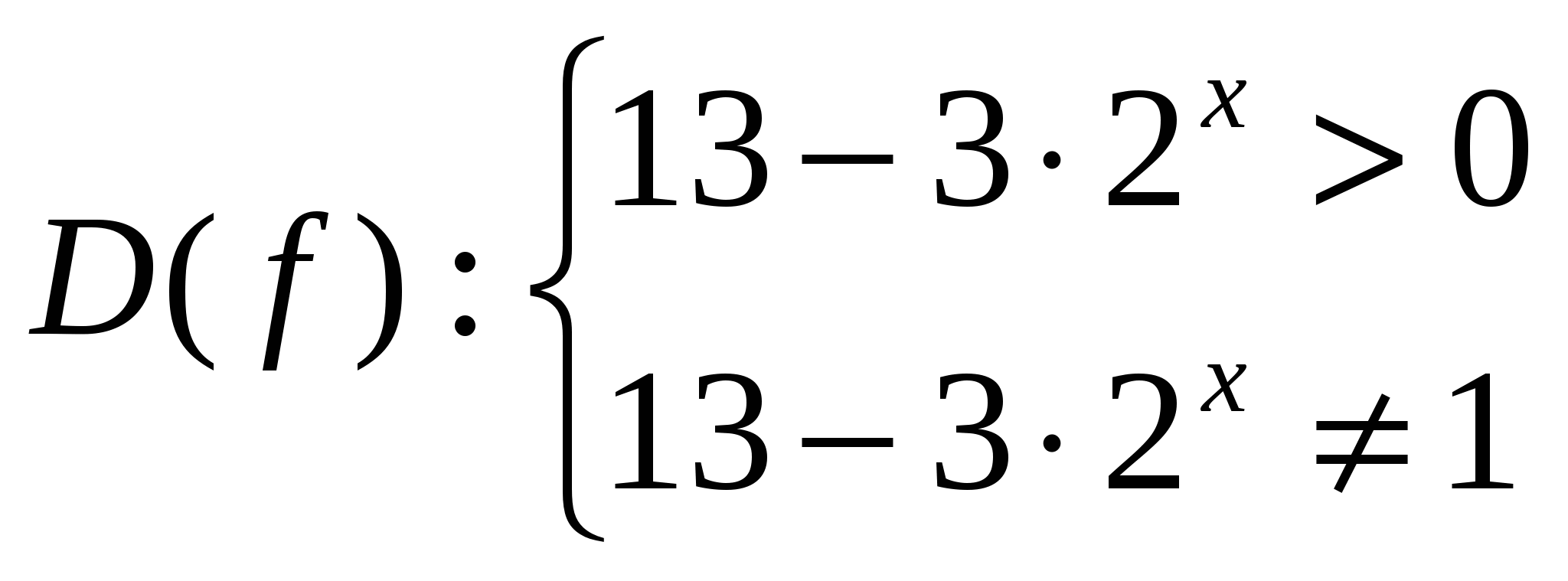
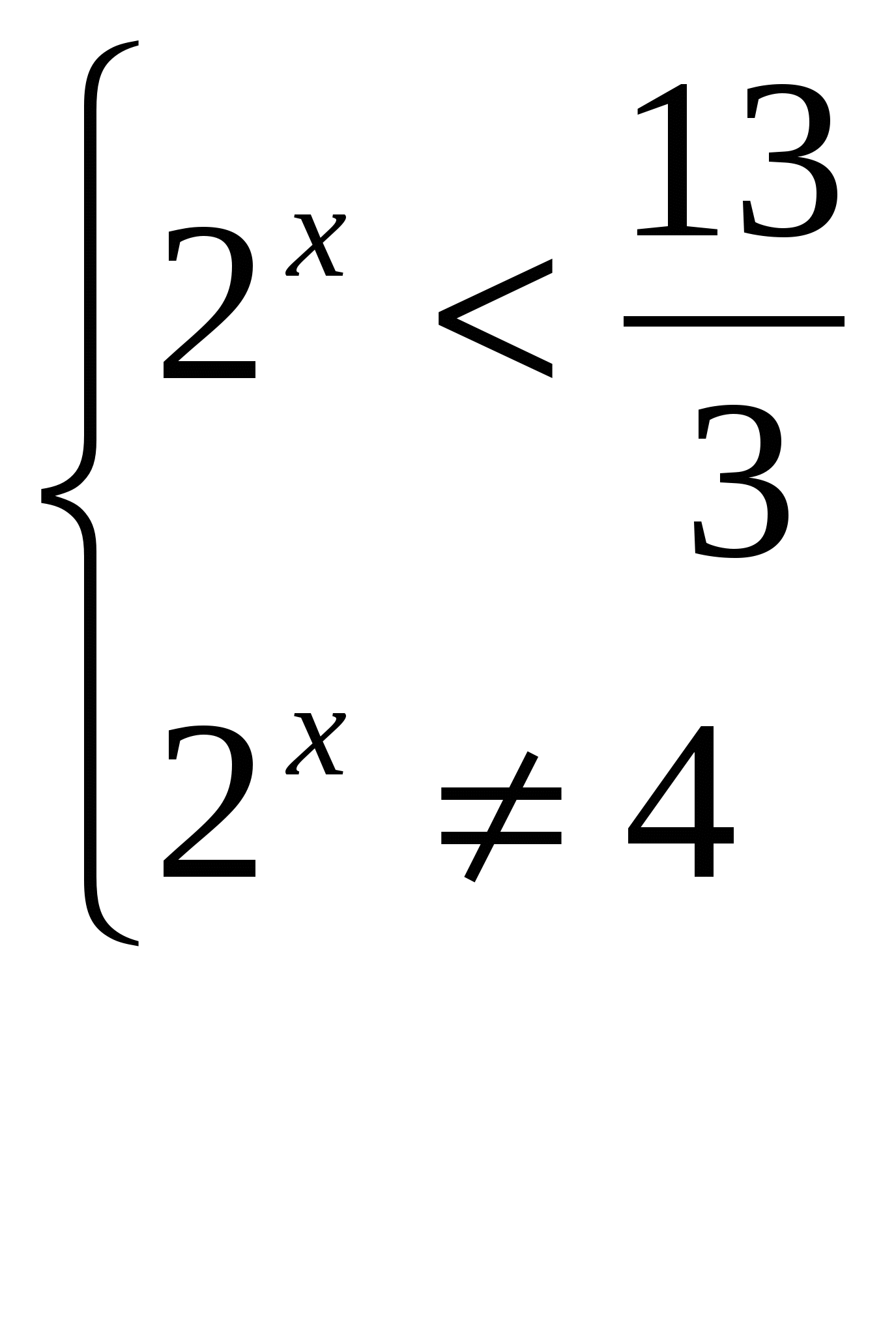
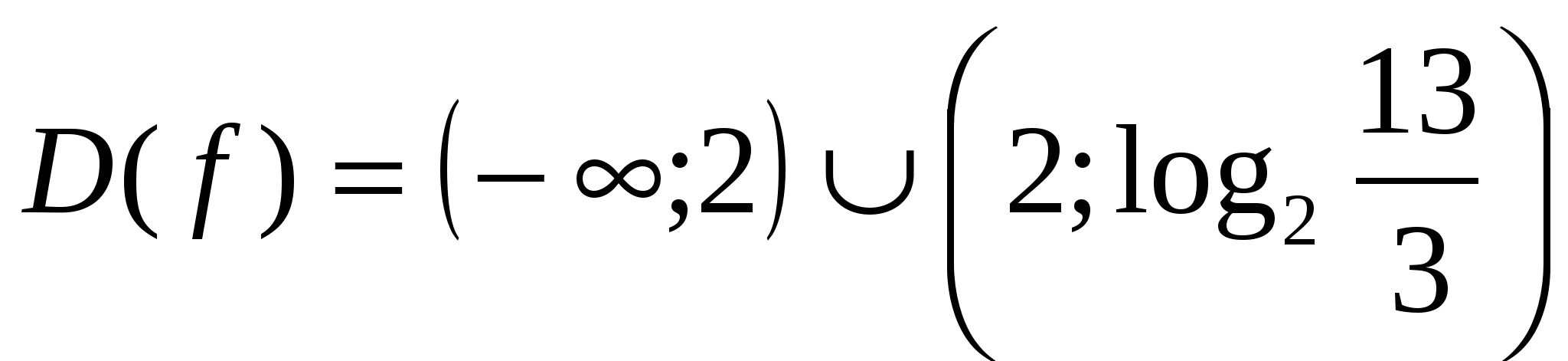
-
Найдем нули функции:
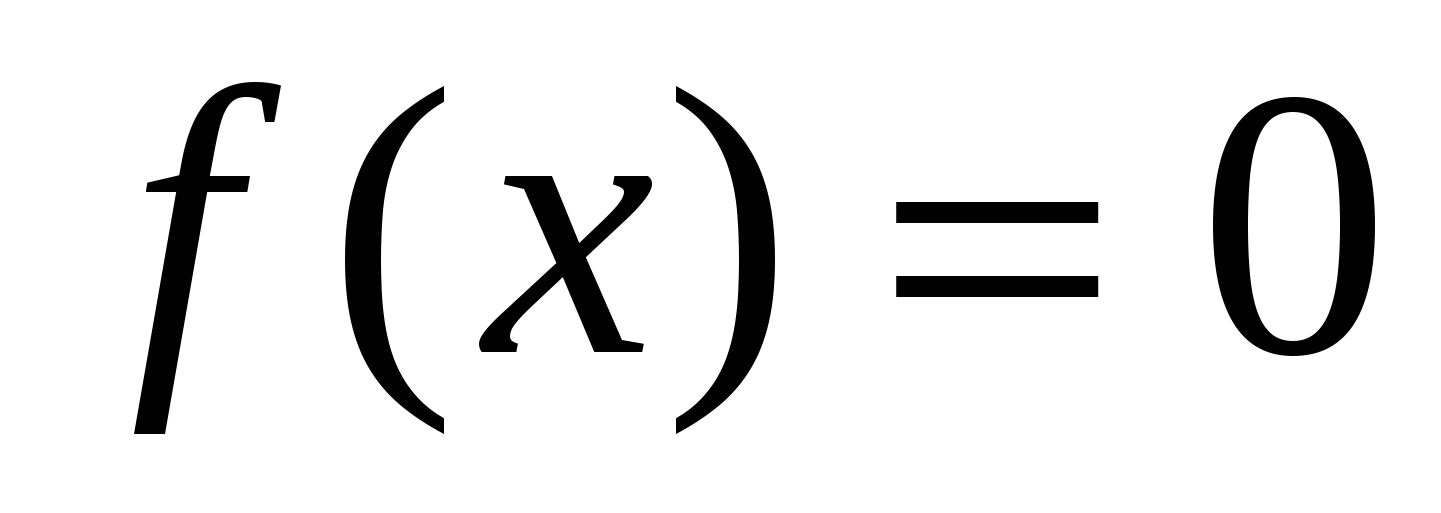
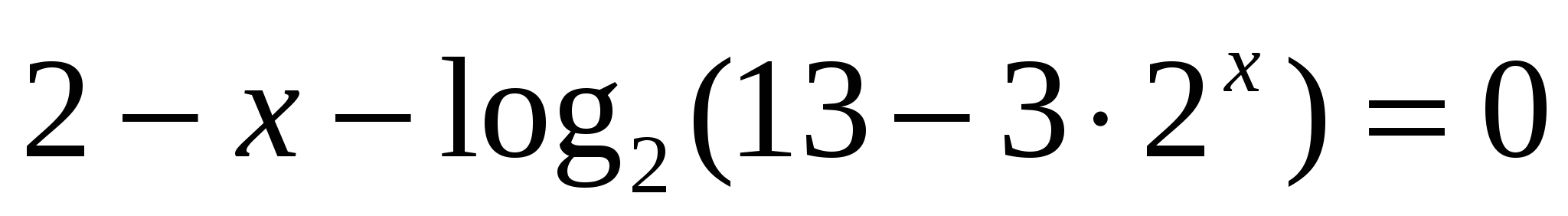
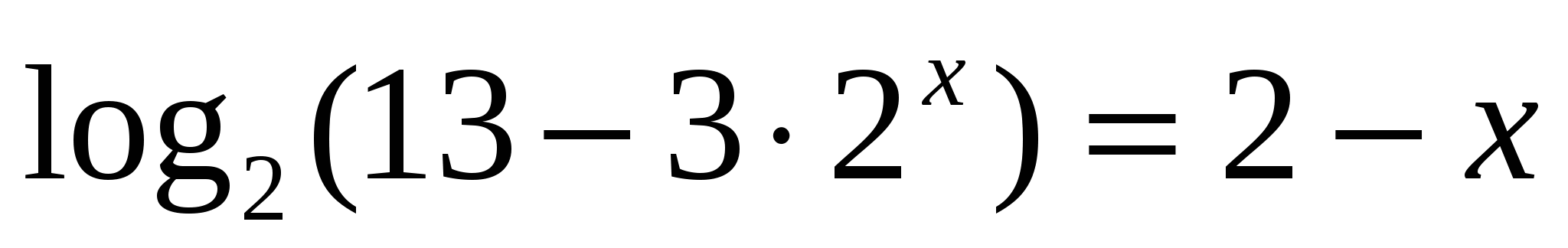
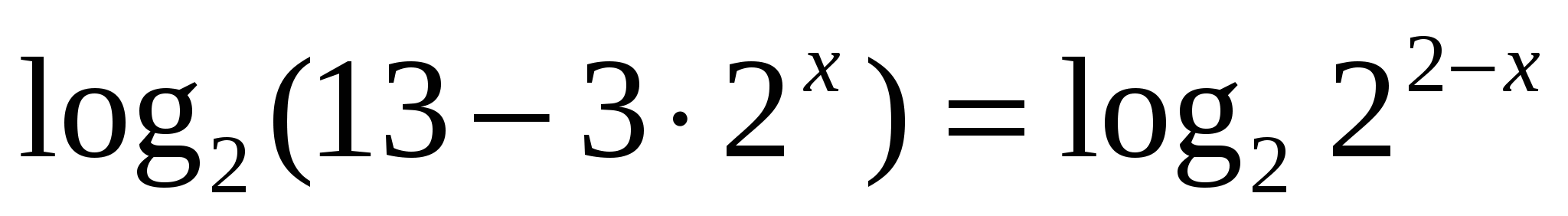
![]()
![]()
![]()
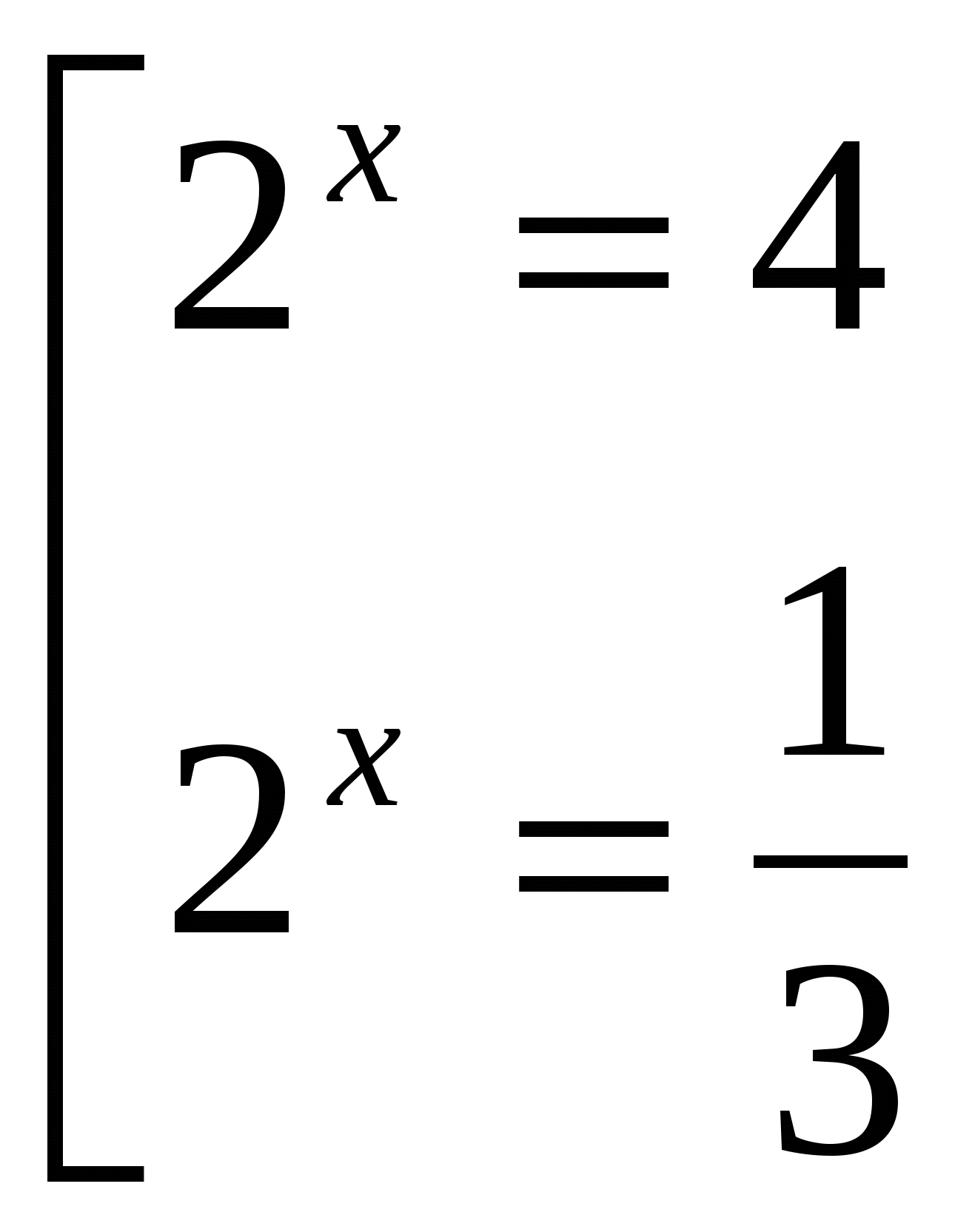
![]()
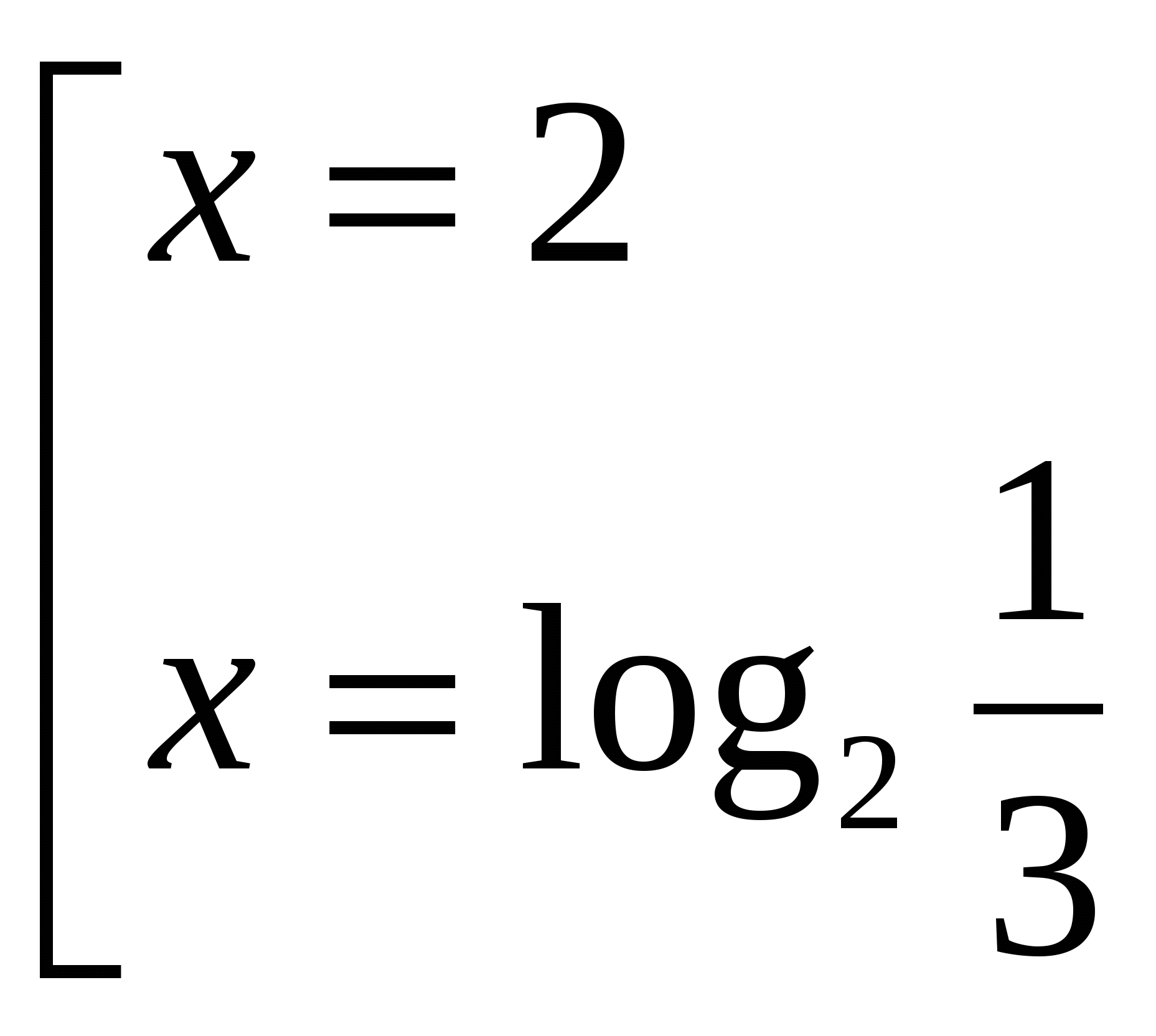
![]()
![]()
-
Определим знаки функции на каждом из промежутков
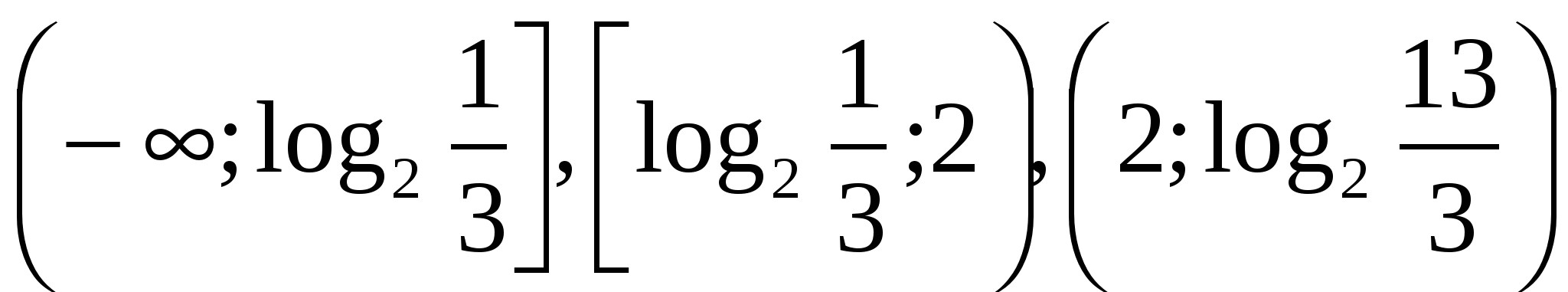
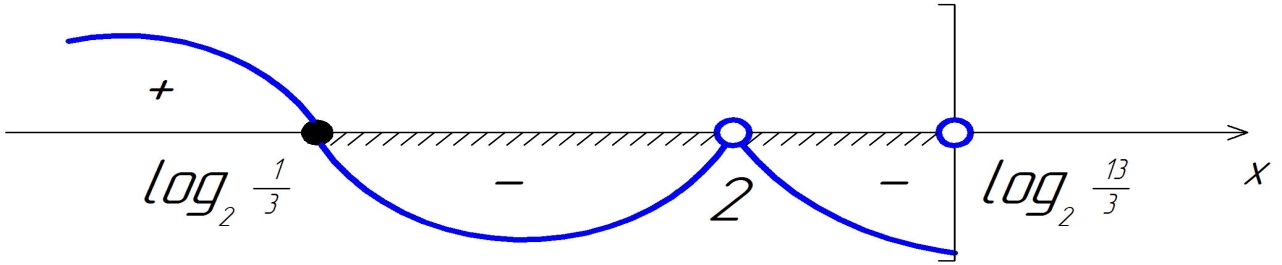
Множеством решений исходного неравенства является объединение промежутков ![]()
Ответ: ![]()
6). Решить неравенство ![]()
Используем метод интервалов для решения данного неравенства
![]()
![]()
![]()
-
Рассмотрим функцию
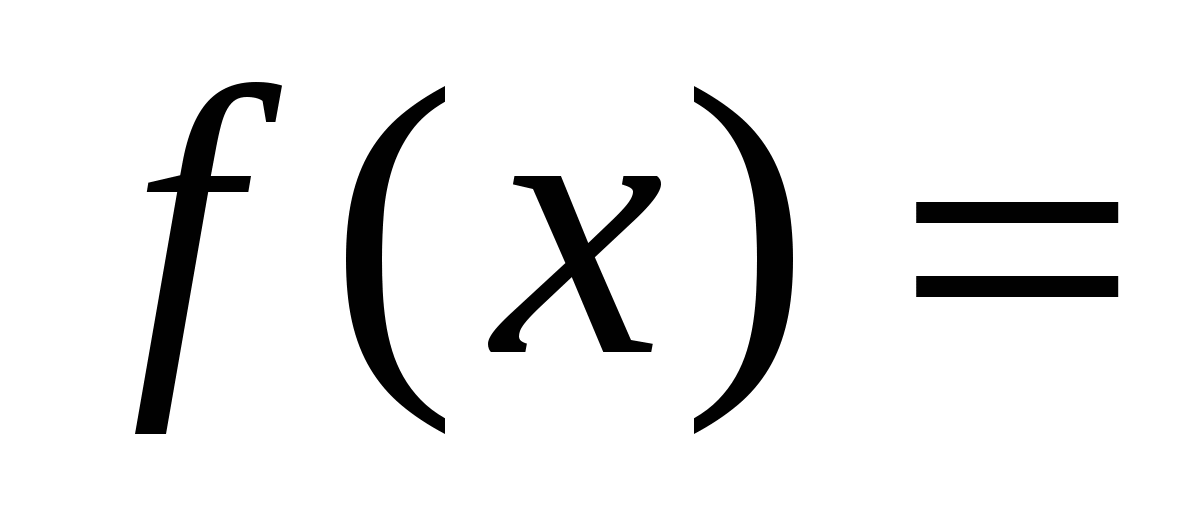
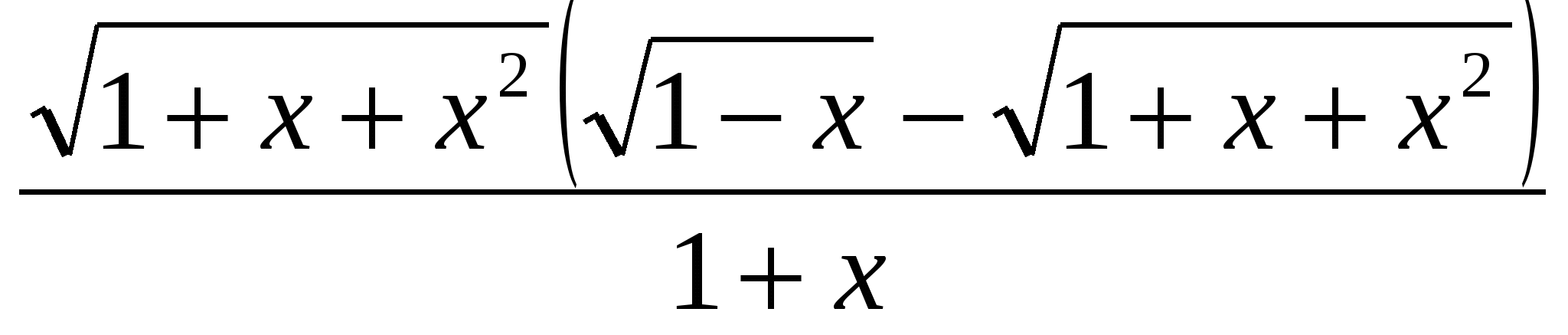
-
Найдем область определения функции
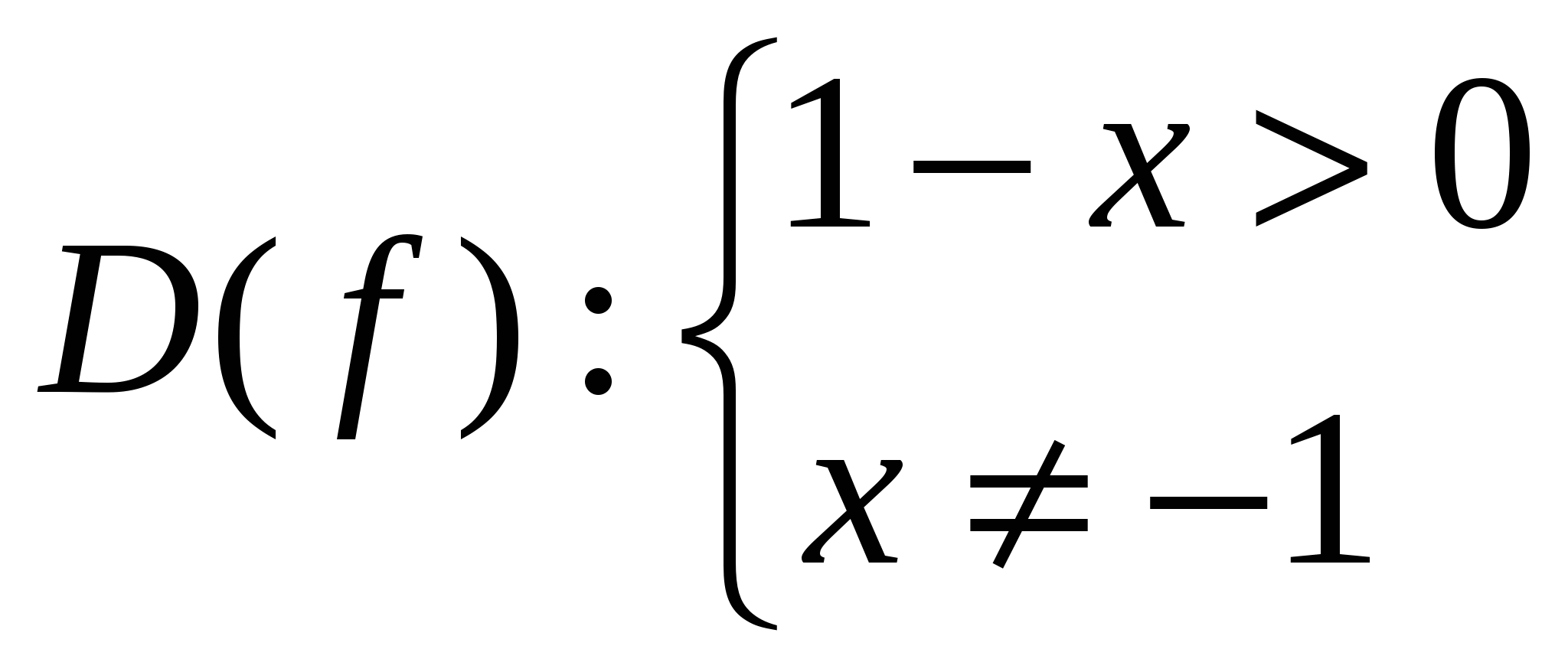
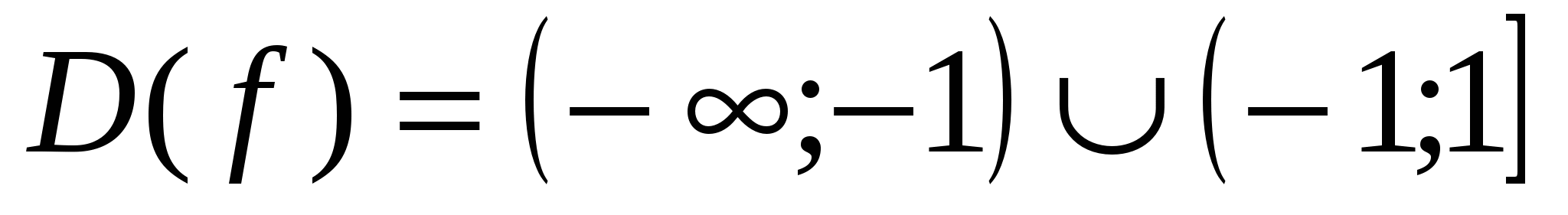
-
Найдем нули функции:
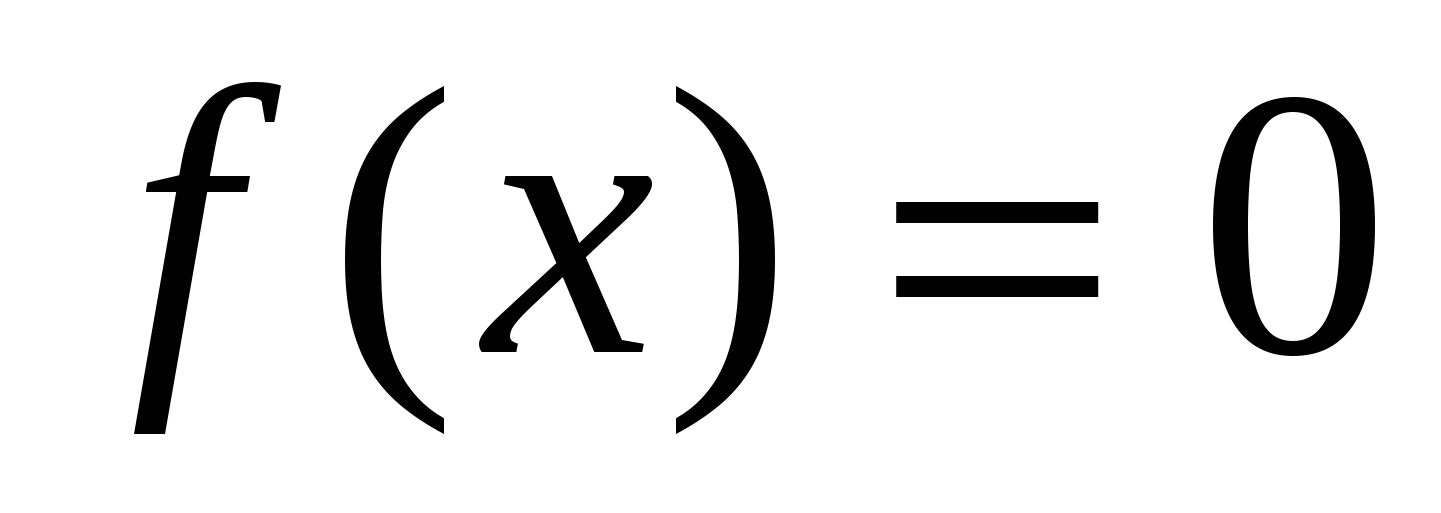
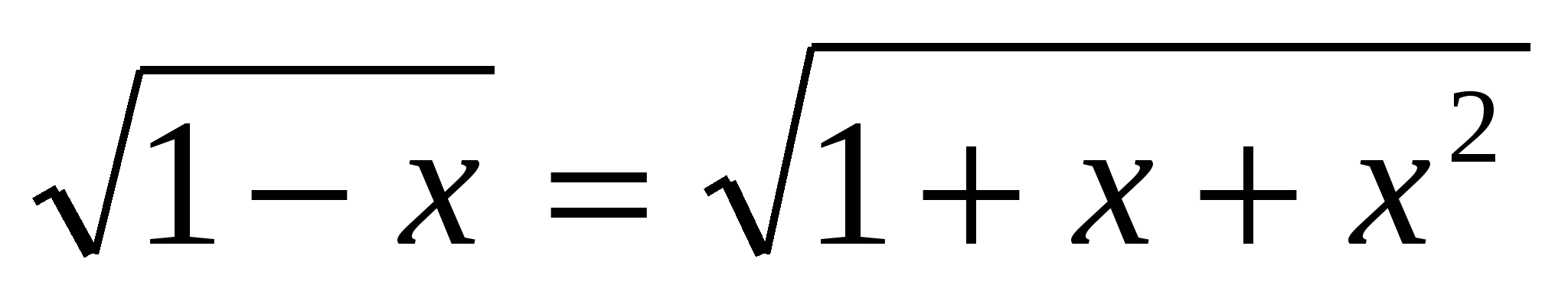
![]()
![]()
![]()
![]()
-
Определим знаки функции на промежутках:
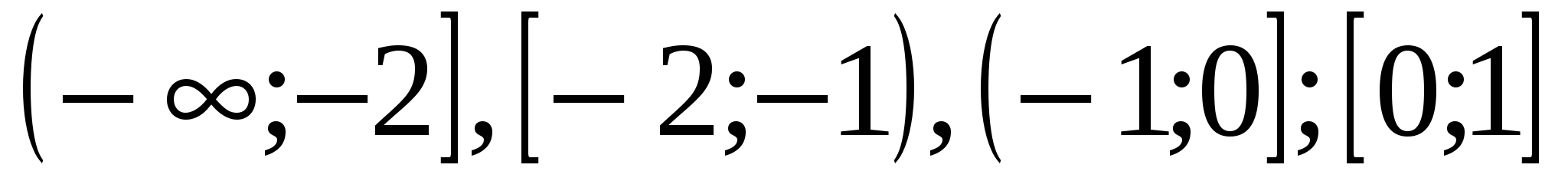

![]()
Следовательно, множеством решений исходного неравенства является объединение промежутков ![]()
Ответ: ![]()
7). Решить неравенство ![]()
![]()
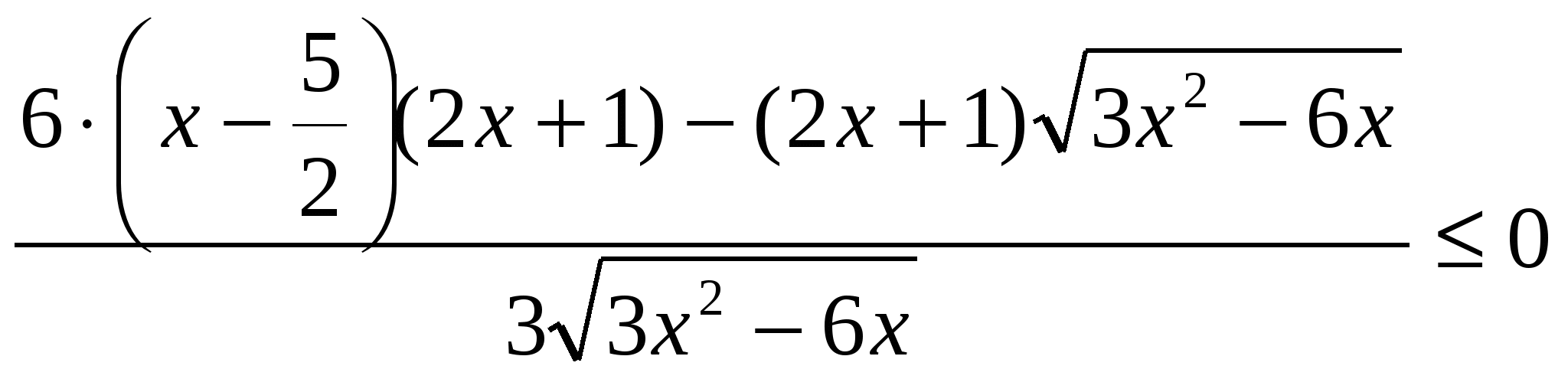
![]()
Используем метод интервалов для решения данного неравенства
-
Рассмотрим функцию
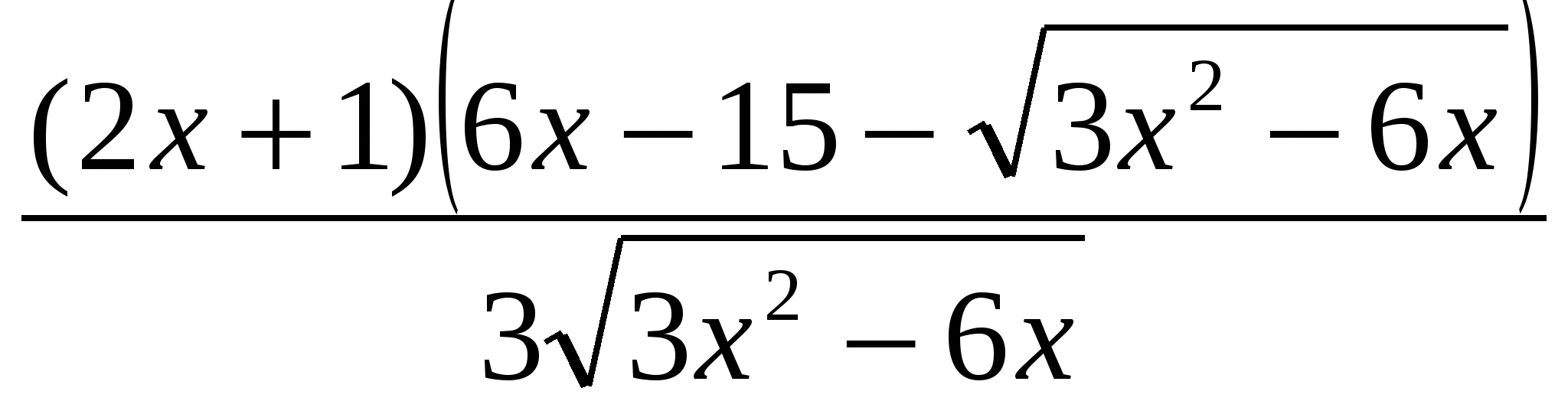
-
Найдем область определения функции
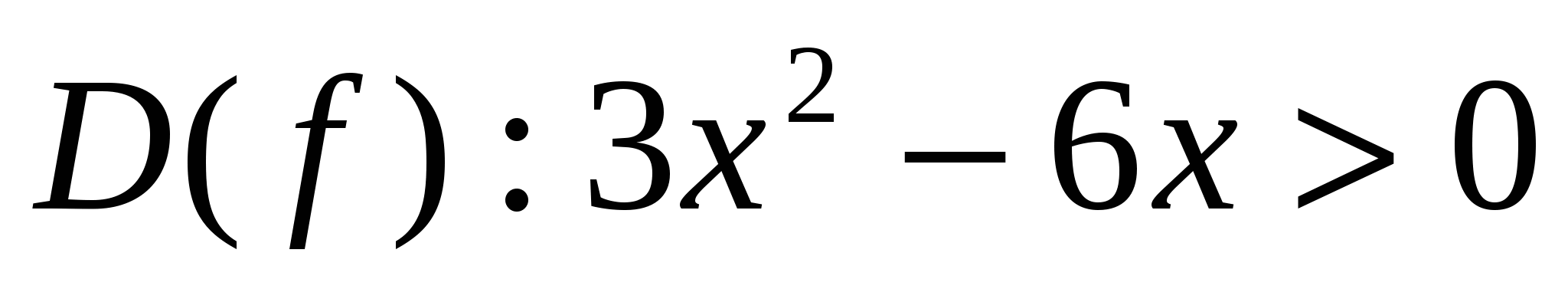
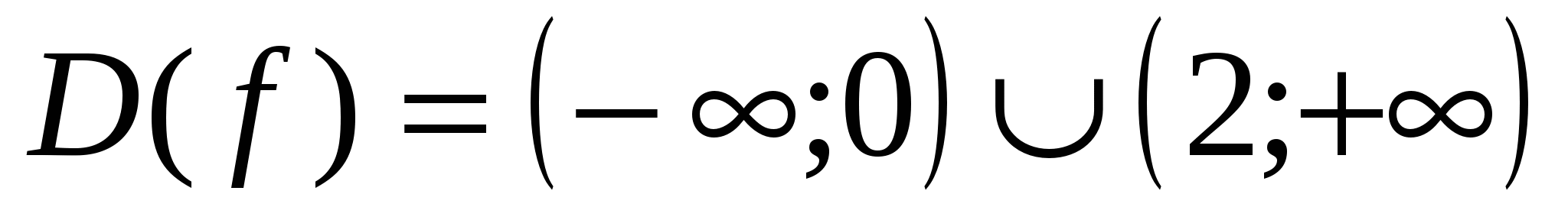
-
Найдем нули функции:
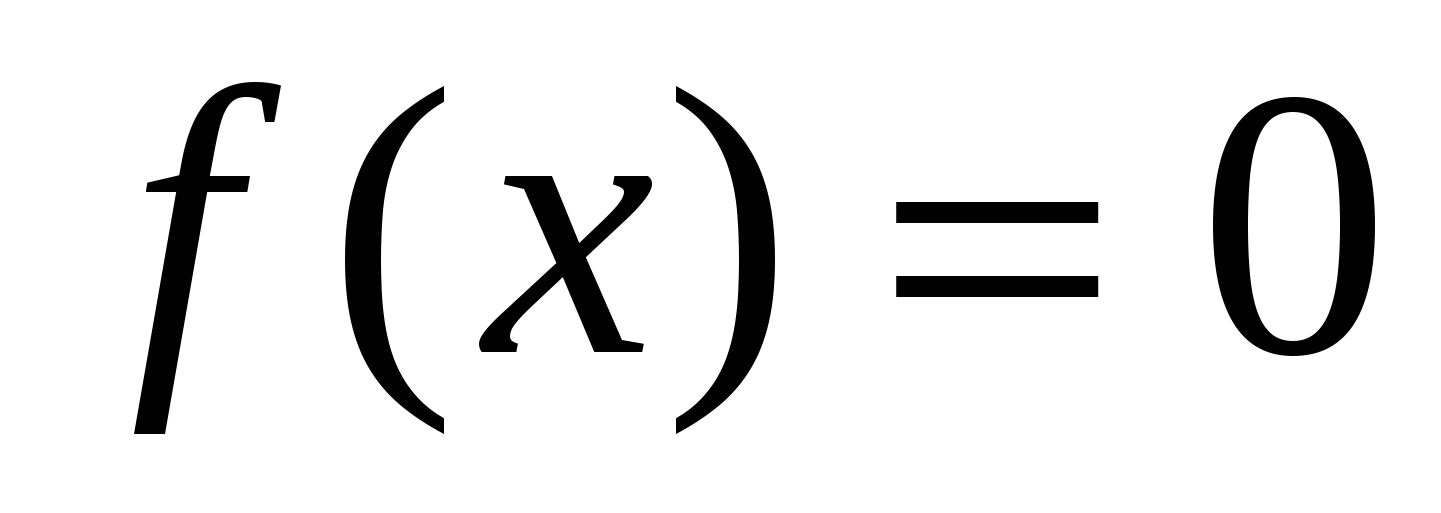
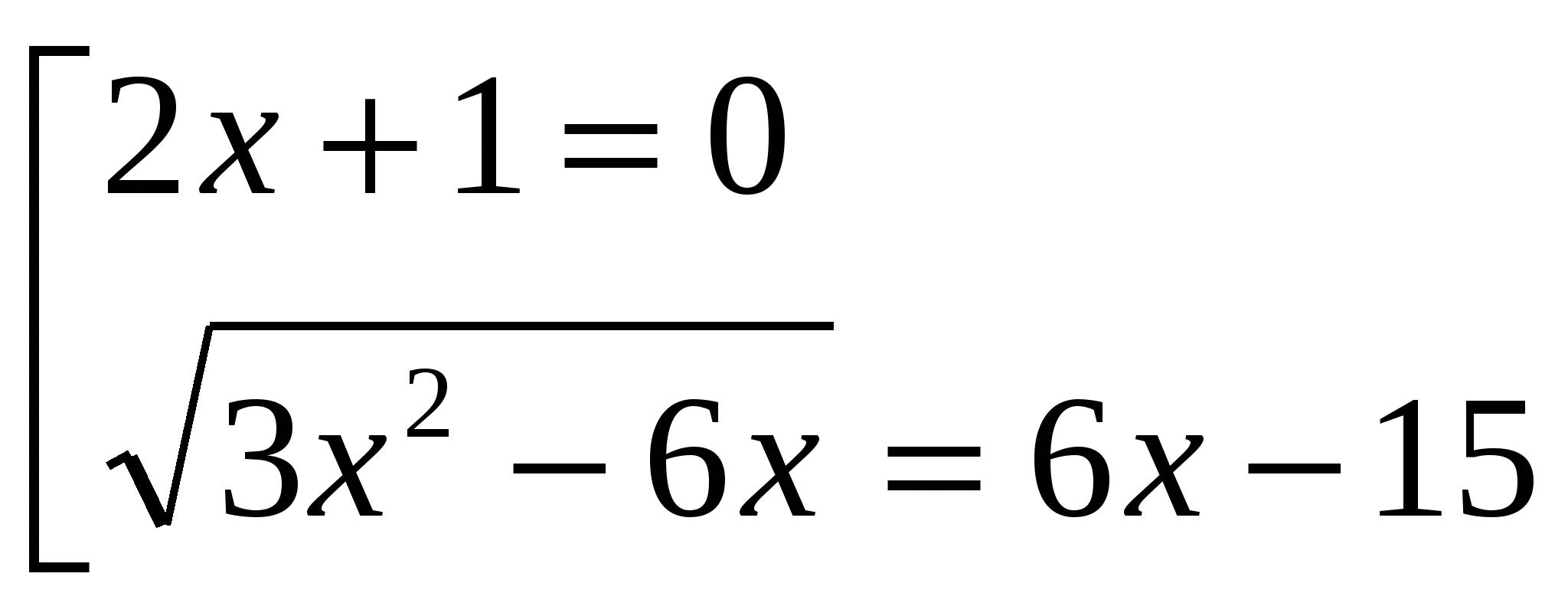
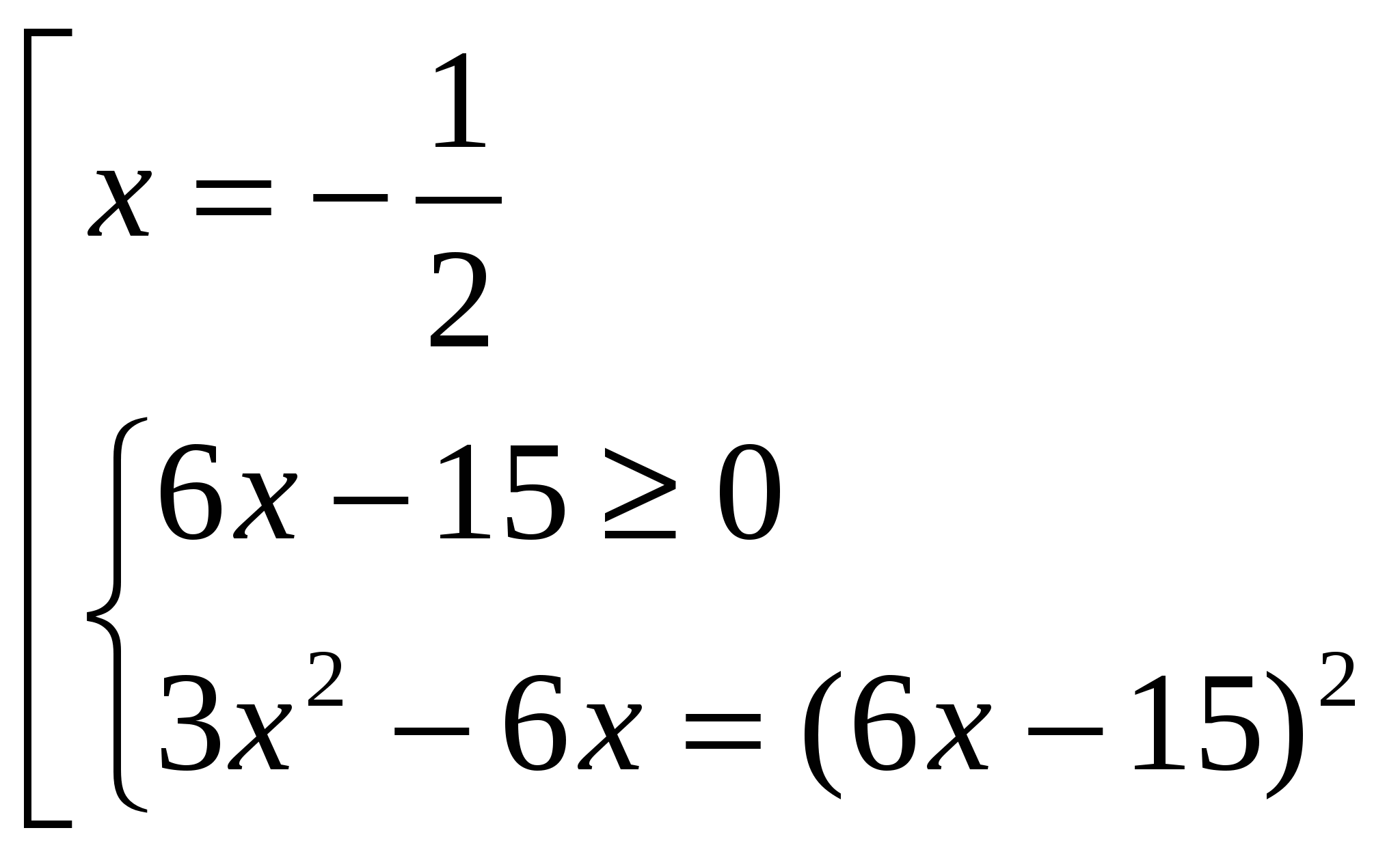
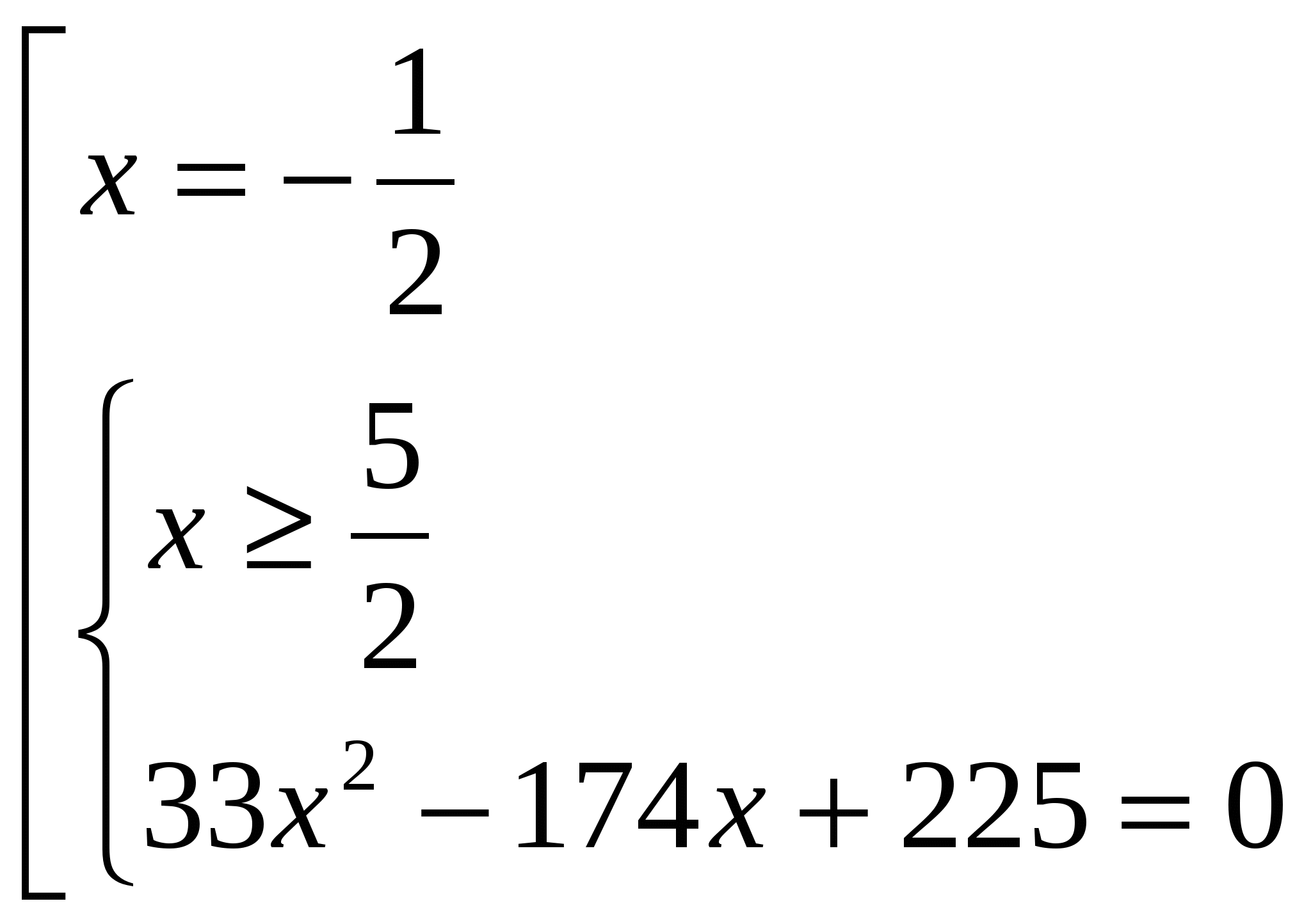
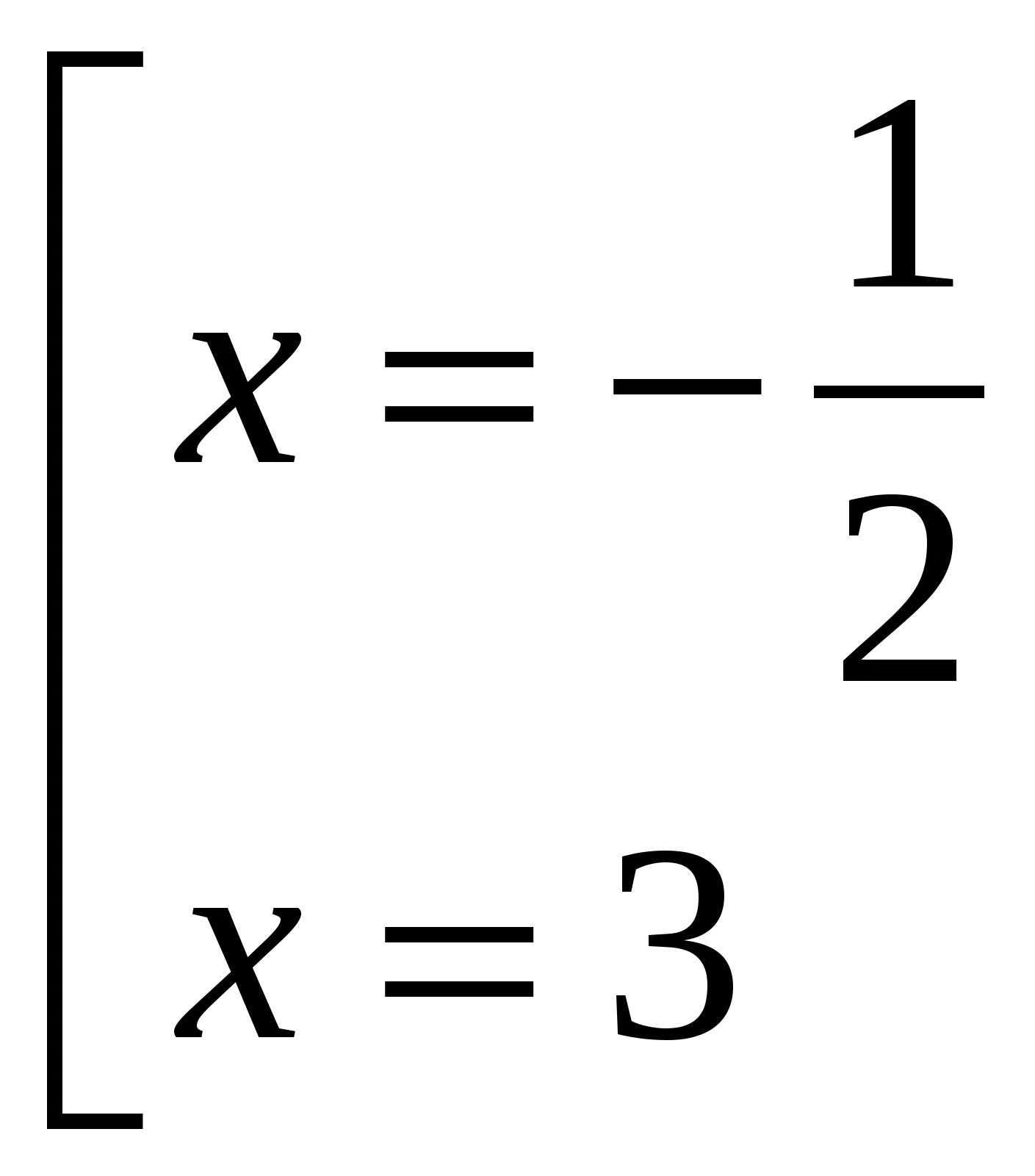
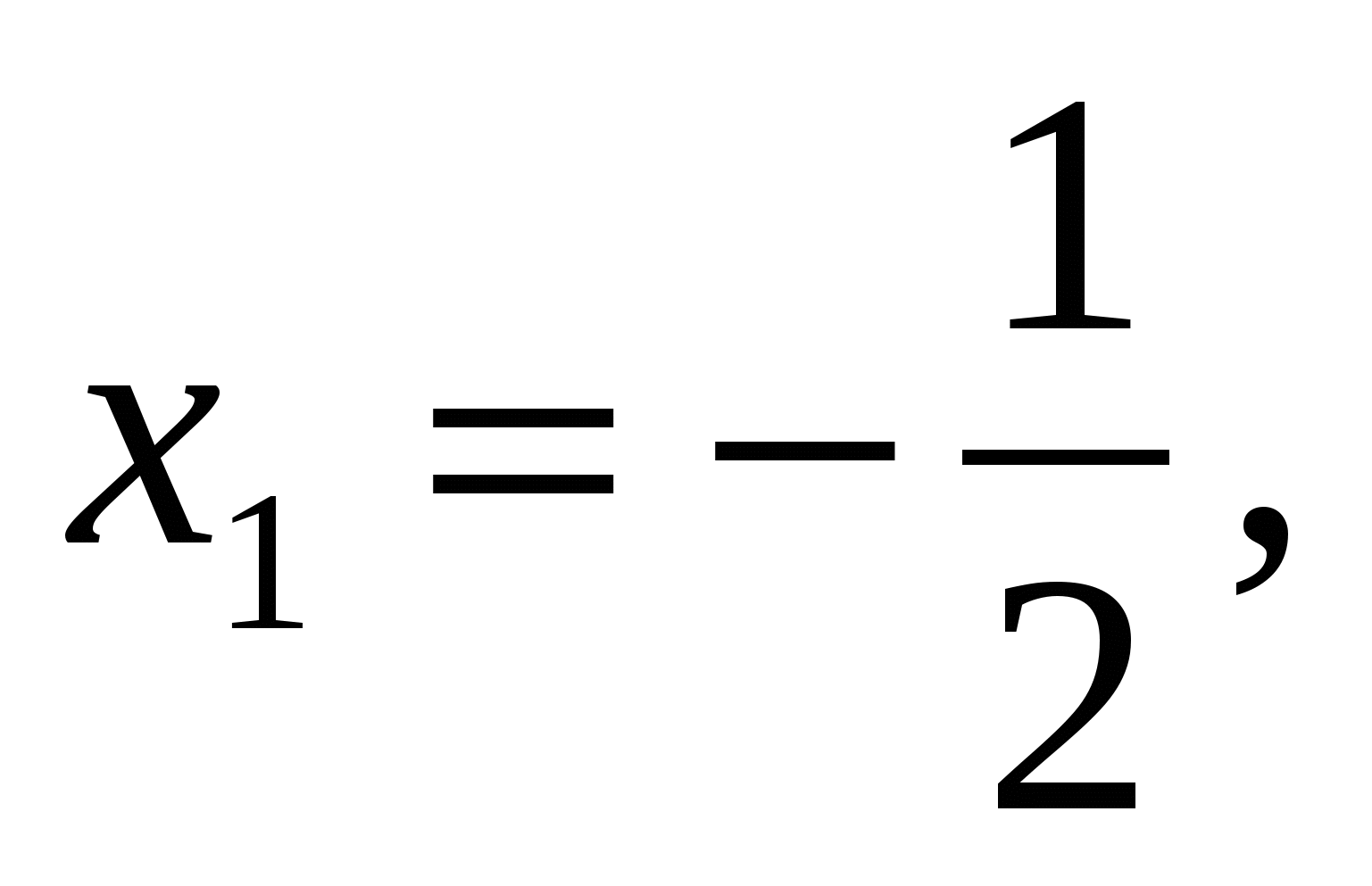
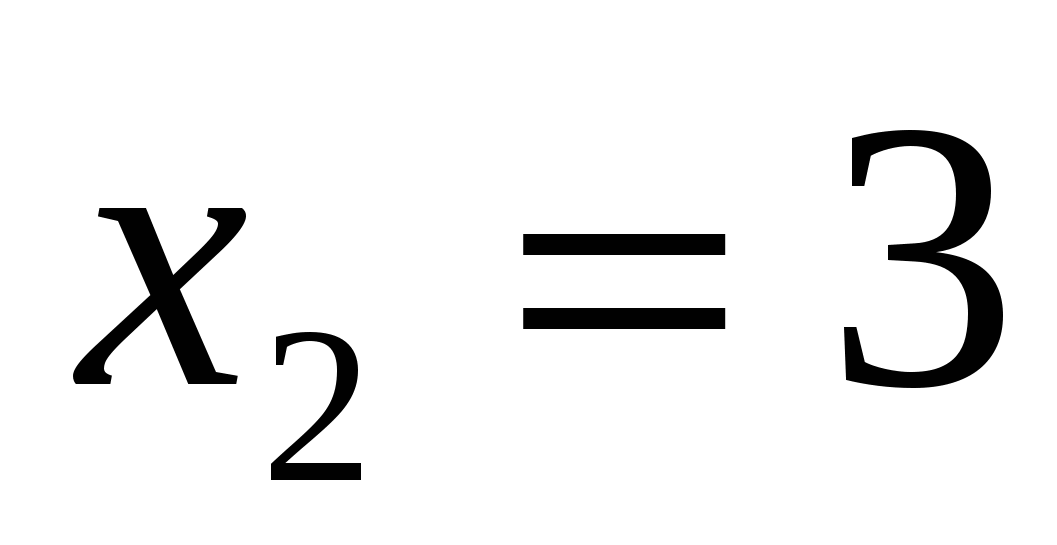
-
Определим знаки функции на промежутках:
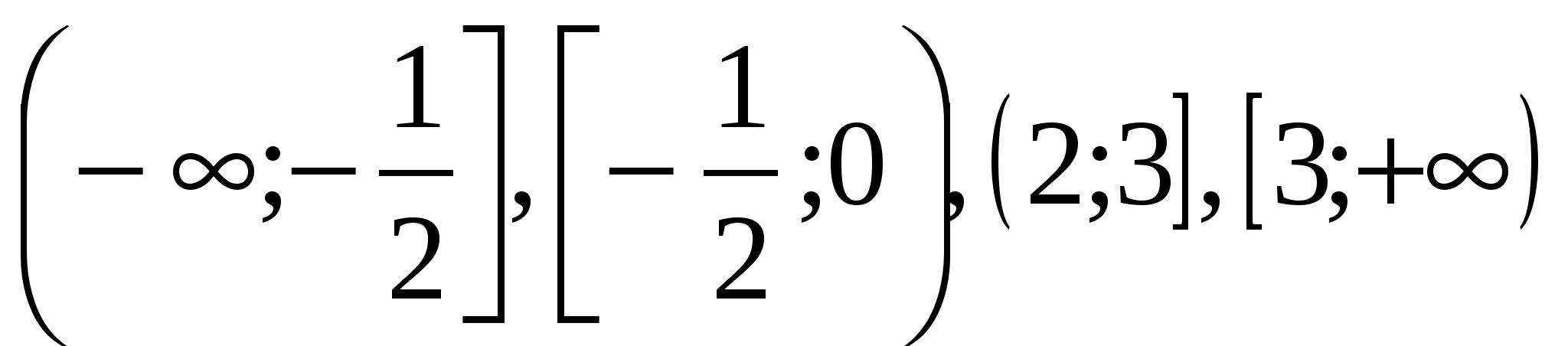
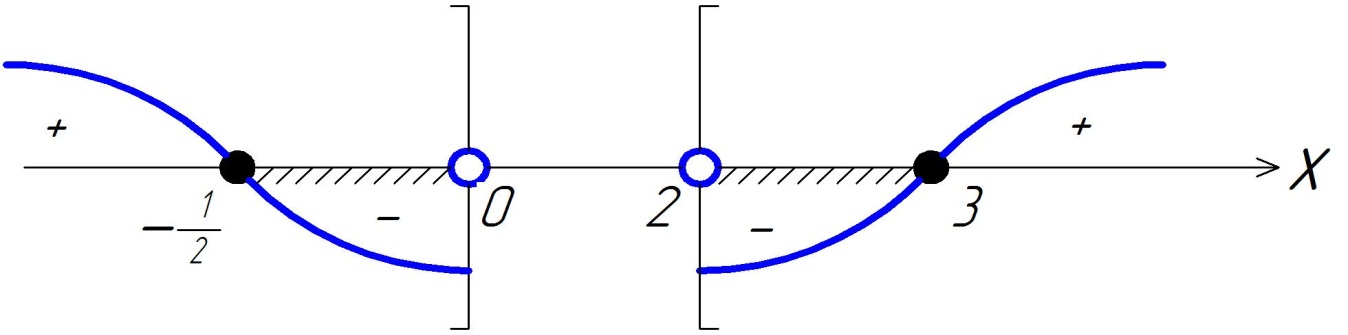
![]() , следовательно, множеством решений исходного неравенства является объединение промежутков
, следовательно, множеством решений исходного неравенства является объединение промежутков ![]()
Ответ: ![]()
![]()
-
Подведение итогов. Задание на дом
Выводы, оценки.
-
Решить неравенства:
а) ![]() , б)
, б) ![]()
в) ![]() г)
г) ![]()
-
Дополнительно (на оценку):
а) ![]() б)
б) ![]()
-
Проверочная работа
Решить неравенства:
-
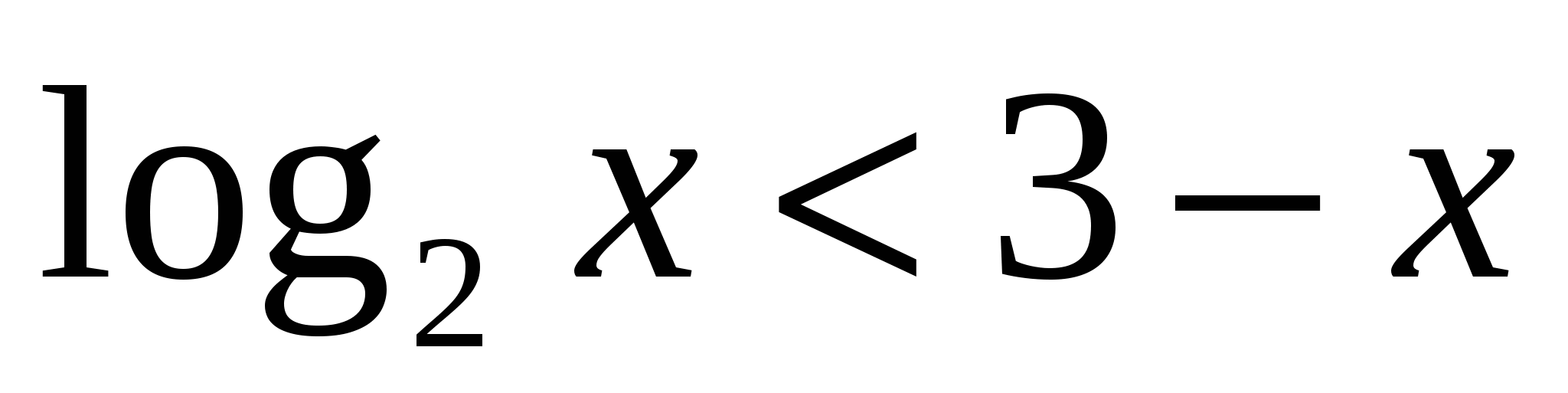 2.
2. 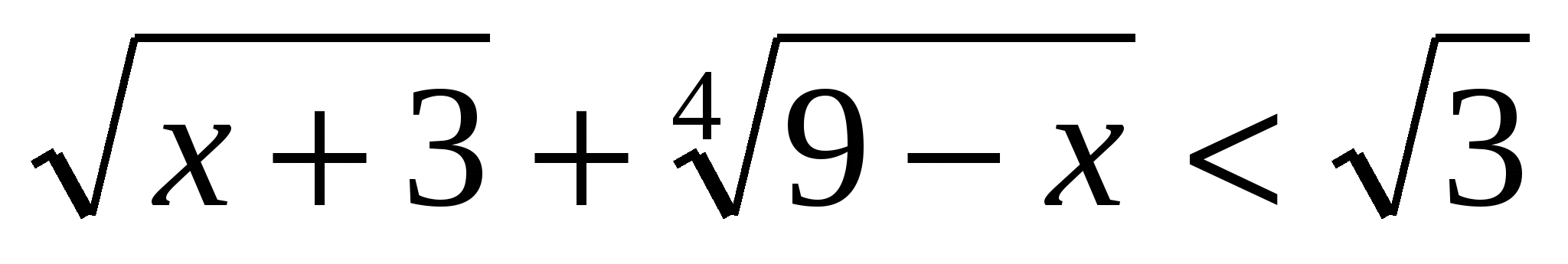
-
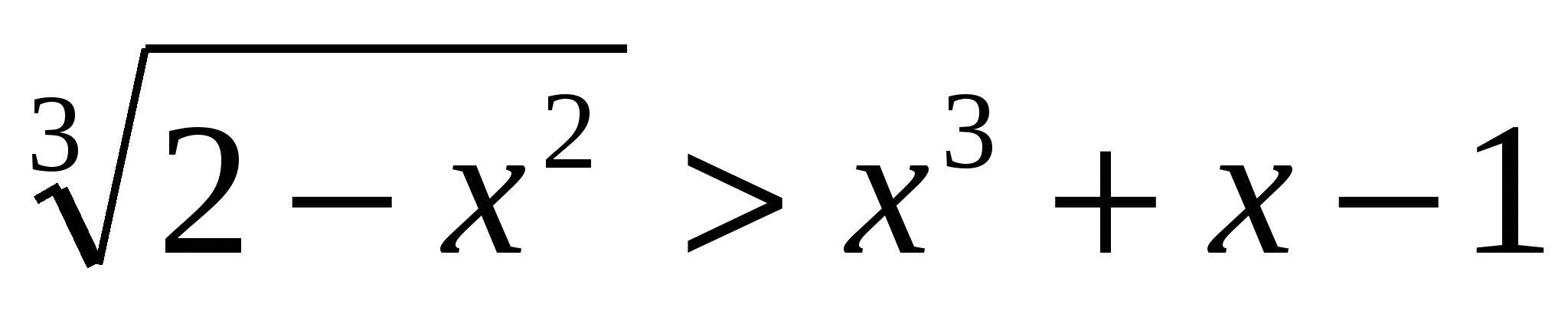 4.
4. 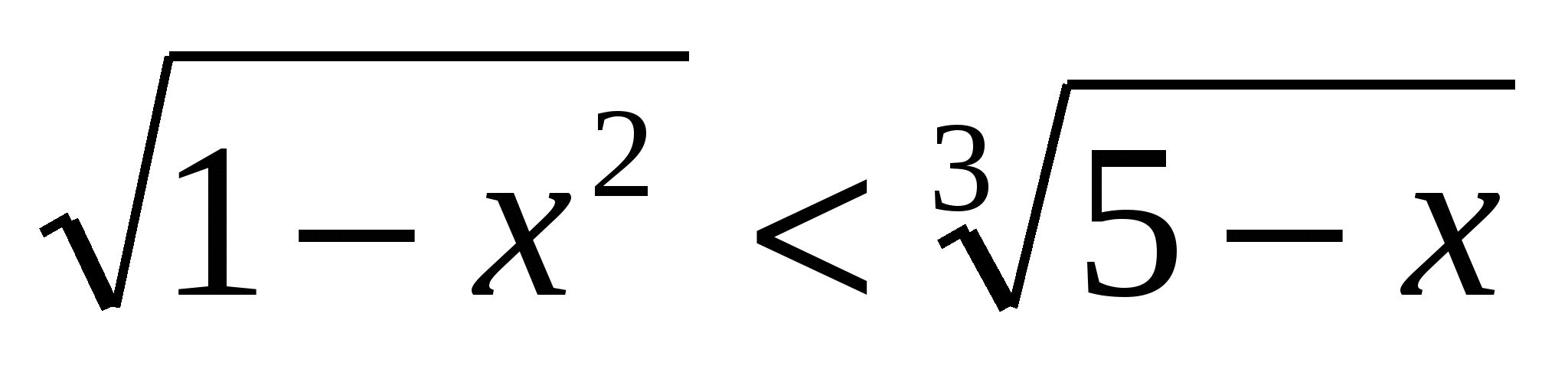
5. ![]() 6.
6. ![]()
Оценка ставится за любые «пять» верно выполненных заданий.
Список использованной литературы
-
Дорофеев Г. В. Обобщение метода интервалов. – Математика в школе, 1969, №3.
-
Математика. Алгебра. Начала математического анализа. Профильный уровень: учебник для 10 класса. М. И. Шабунин, А. А. Прокофьев. – М.: БИНОМ. Лаборатория знаний. 2007.
-
Панферов В. С., Сергеев И. Н. ЕГЭ – 2010. Математика. Задача С3, под редакцией А. Л. Семенова и И. В. Ященко. – М.: МЦНМО, 2010.
-
Садовничий Ю. В. ЕГЭ. Практикум по математике: Решение уравнений и неравенств. Преобразование алгебраических выражений. – М.: Издательство «Экзамен», 2012.
Здесь представлен конспект к уроку на тему «Организация повторения по алгебре в 11 профильном классе для подготовки к решению заданий С3 в ЕГЭ», который Вы можете бесплатно скачать на нашем сайте. Предмет конспекта: Алгебра (11 класс). Также здесь Вы можете найти дополнительные учебные материалы и презентации по данной теме, используя которые, Вы сможете еще больше заинтересовать аудиторию и преподнести еще больше полезной информации.

