Презентация "Комплексные числа" (10 класс) по математике – проект, доклад

Комплексные числа

доклад

Содержание

Определение 3 Стандартная модель 4 Матричная модель 6 Арифметические действия 7 Геометрическая модель 9 Модуль и аргумент 11 Множество комплексных чисел с арифметическими действиями 13 Сопряжённые числа 14 Показательная форма 18 Формула Муавра 19 Извлечение корней из комплексного числа 20

№ стр.

Определение

Комплексные числа представляются в виде выражения: z = x + iy, где x, y – вещественные числа; x – действительная часть числа z (Rez); y – мнимая часть числа z (Imz); i – мнимое число (величина, для которой выполняется равенство i2=-1).

Стандартная модель

Комплексное число z можно определить как упорядоченную пару вещественных чисел; запись z = x + iy следует понимать как удобный способ записи такой пары. Введём операции сложения и умножения таких пар следующим образом:

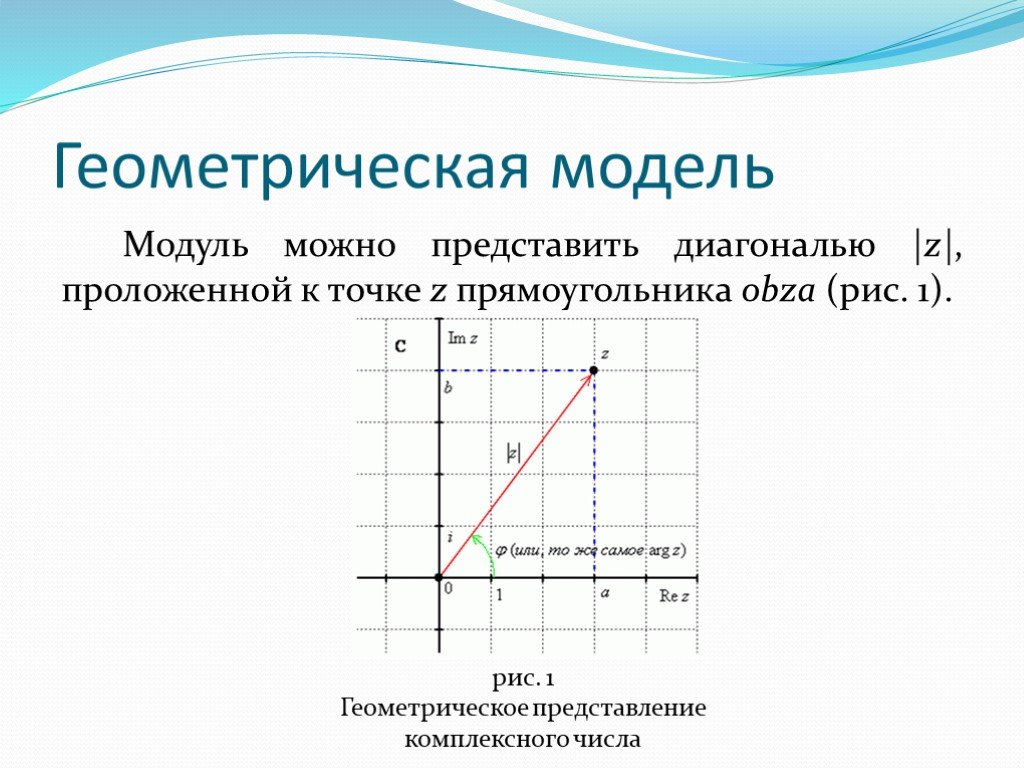
Вещественные числа являются в этой модели подмножеством множества комплексных чисел и представлены парами вида (x, 0), причём операции с такими парами согласованы с обычными сложением и умножением вещественных чисел: Ноль представляется парой 0 = (0, 0); Единица - -1 = (-1, 0).

Матричная модель

Комплексные числа можно также определить как: подкольцо кольца вещественных матриц 2×2 вида с обычным матричным сложением и умножением. Действительной единице будет соответствовать мнимой единице —

Арифметические действия

Сравнение x + iy = a + ib равны тогда и только тогда, когда x = a, y = b; Сложение (x + iy) + (a + ib) = (x + a) + (y + b)i; Вычитание (x + iy) – (a + ib) = (x - a) + (y - b)i;

Умножение (x + iy) ∙ (a + ib) = xa + xib + aiy + bi2y = (xa - yb) + (ya + xb)i; Деление В частности

Геометрическая модель

Любое комплексное число (кроме нуля) можно записать в тригонометрической форме: z = |z| ∙ (cosφ + i · sinφ), где |z| - модуль комплексного числа; φ – аргумент комплексного числа. Модулем комплексного числа называется расстояние от начала координат до соответствующей точки комплексной плоскости.

Модуль можно представить диагональю |z|, проложенной к точке z прямоугольника obza (рис. 1).

рис. 1 Геометрическое представление комплексного числа

Модуль и аргумент

По теореме Пифагора легко вывести формулу для нахождения модуля комплексного числа: Угол φ между положительной полуосью действительной оси Rez и радиус-вектором |z|, проведённым из начала координат к соответствующей точки, является аргументом комплексного числа z. Аргумент не определён для единственного числа: z = 0.

Из этого определения следует, что: Если a = 0, то z является мнимым числом; Если b = 0, то z является действительным числом.

Множество комплексных чисел с арифметическими действиями

Множество всех комплексных чисел с арифметическими операциями является полем и обычно обозначается символом C. Для любых z, z1, z2 є C имеют место следующие свойства модуля: |z| ≥ 0; |z1 + z2| ≤ |z1| + |z2|; |z1 ∙ z2|= |z1| ∙ |z2|;

Сопряжённые числа

Если комплексное число z = x + iy, то является сопряжённым к z. На комплексной плоскости сопряжённые числа получаются зеркальным отражением друг друга относительно вещественной оси (рис. 2). Модуль сопряжённого числа такой же, как у исходного, а их аргументы отличаются знаком.

Переход к сопряжённому числу можно рассматривать как одноместную операцию: Произведение и сумма комплексно-сопряженных чисел есть действительное число: ; . Другие соотношения: ; .

Умножение числителя и знаменателя комплексной дроби при комплексном знаменателе на сопряжённое к знаменателю выражению используется для устранения комплексности знаменателя, что позволяет выразить выражение в канонической форме комплексного числа или функции.

Рис. 2 Геометрическое представление сопряжённых чисел где r – модуль числа z, второе обозначение |z|

Показательная форма

Применяя к тригонометрической форме комплексного числа z = |z| ∙ (cosφ + i · sinφ) формулу Эйлера, получим показательную форму: z = |z|eiφ, где eiφ - расширение экспоненты для случая комплексного показателя степени. Отсюда вытекают следующие широко используемые равенства:

Формула Муавра

Формула Муавра помогает возводить в целую степень ненулевое комплексное число, представленное в тригонометрической форме. где r — модуль; φ — аргумент комплексного числа. В современной символике она опубликована Эйлером в 1722 году. Приведенная формула справедлива при любом целом n, необязательно положительном.

Извлечение корней из комплексных чисел

Аналогичная формула применима также и при вычислении корней n-ой степени из ненулевого комплексного числа: где n > 1 и k = 0, 1, …, n – 1. Отметим, что корни n-й степени из ненулевого комплексного числа всегда существуют и их количество равно n. На комплексной плоскости, как видно из формулы, все эти корни являются вершинами правильного n-угольника, вписанного в окружность радиуса с центром в начале координат (рис. 3).

Извлечение корней из комплексного числа

Рис. 3 Корни пятой степени из единицы (вершины пятиугольника)