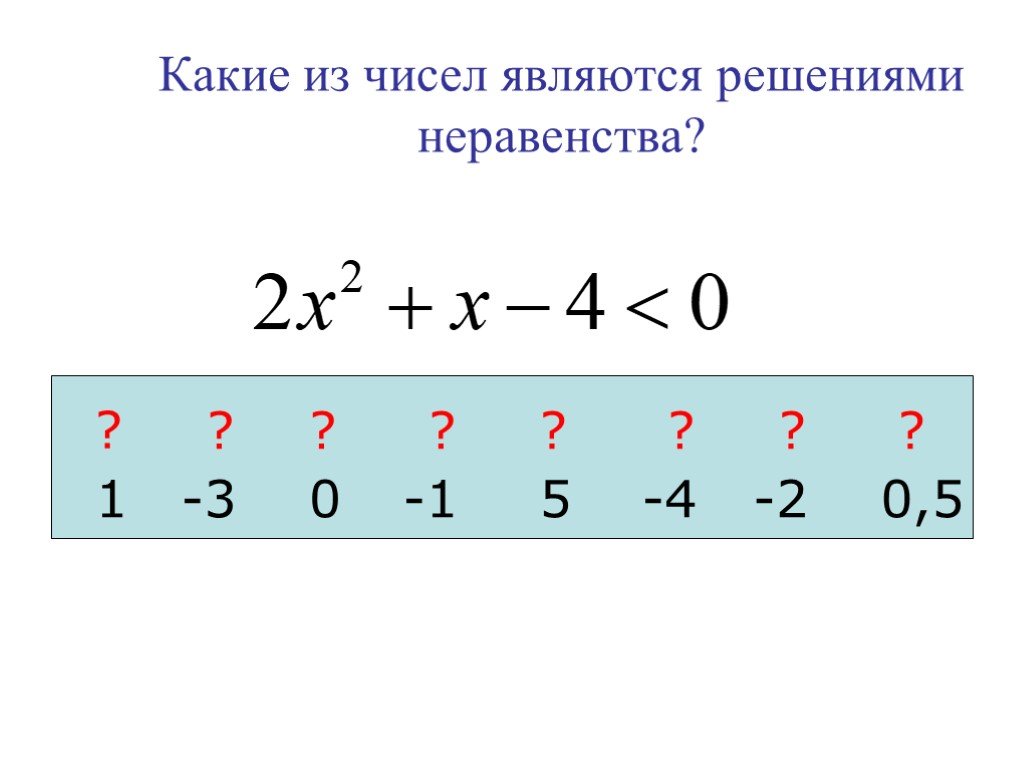
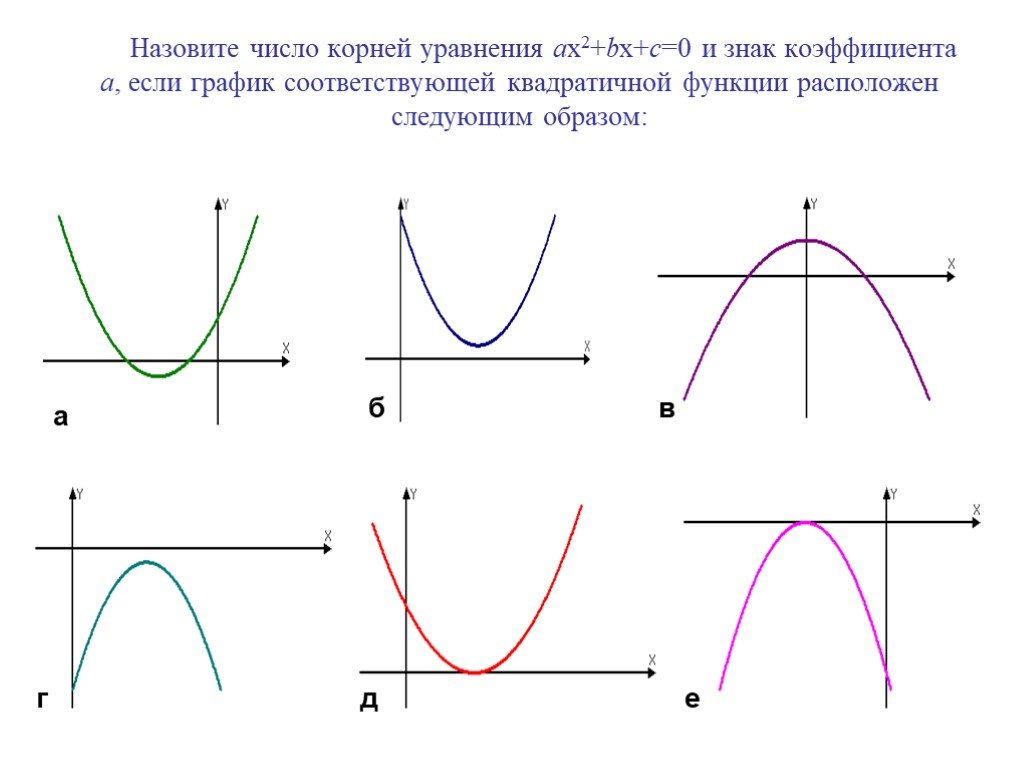
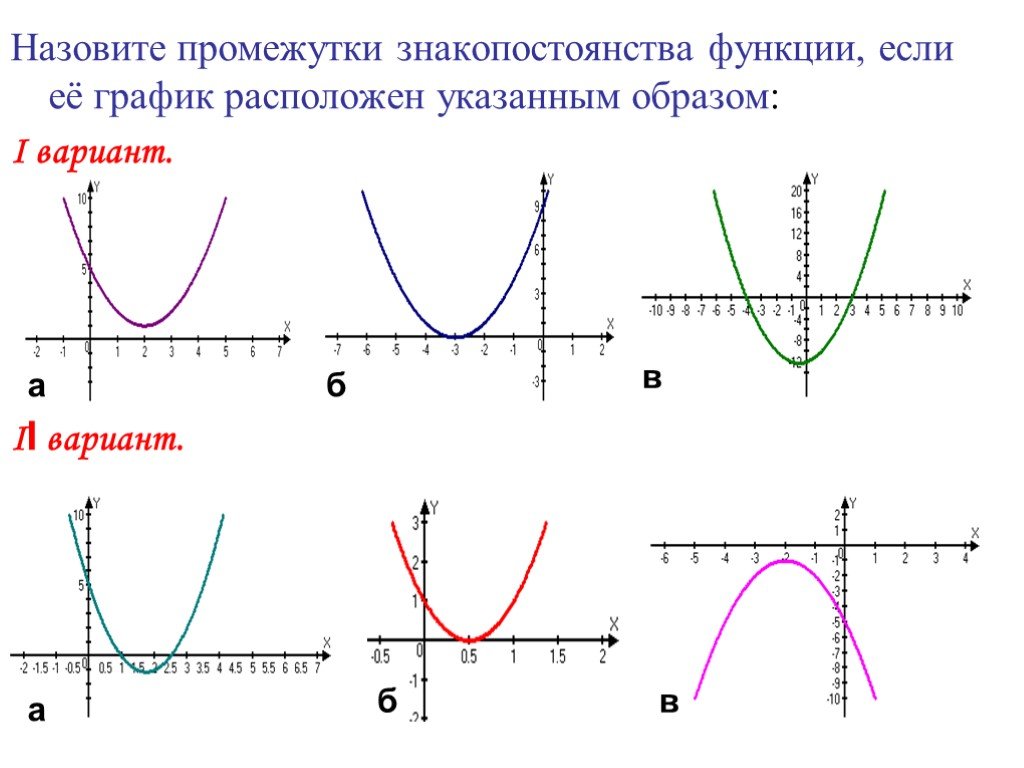
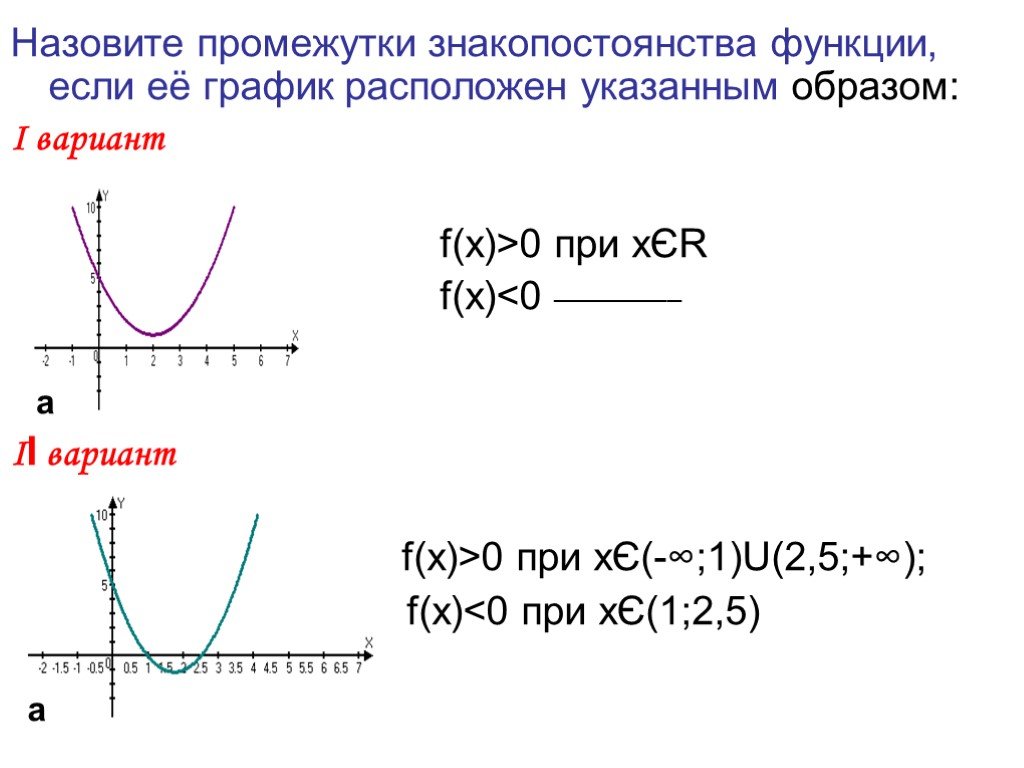
Презентация "Графики квадратичной функции" по математике – проект, доклад
Презентацию на тему "Графики квадратичной функции" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 38 слайд(ов).
Слайды презентации
Список похожих презентаций
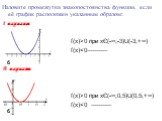
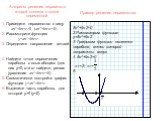
Алгоритм построения графика квадратичной функции
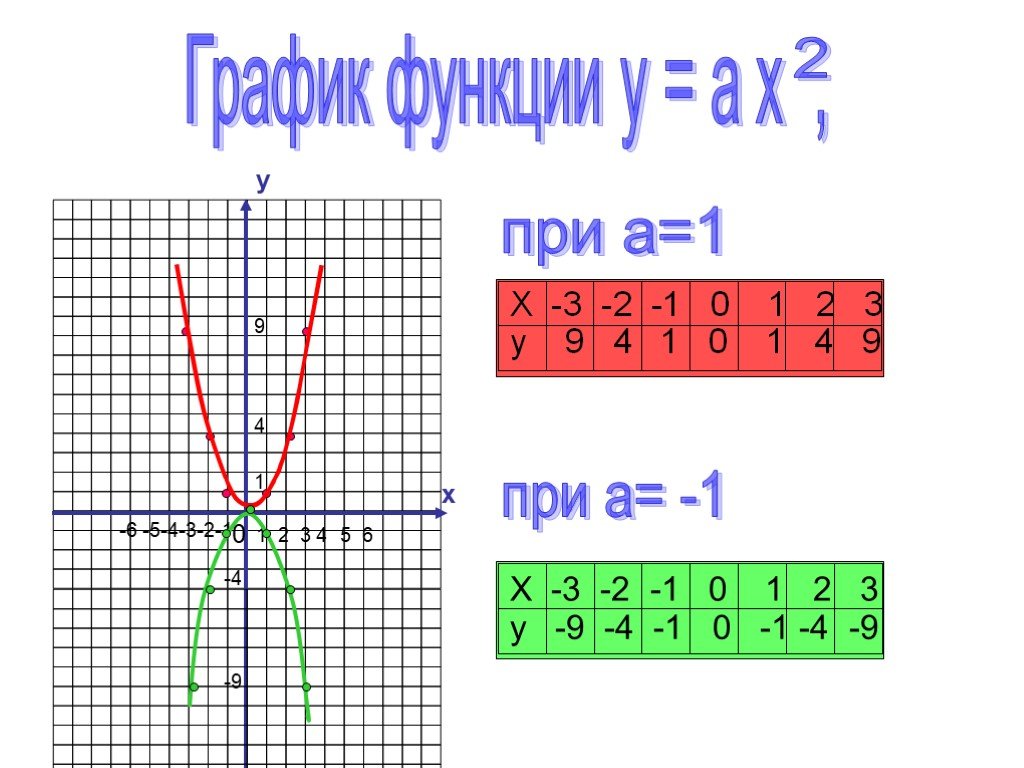
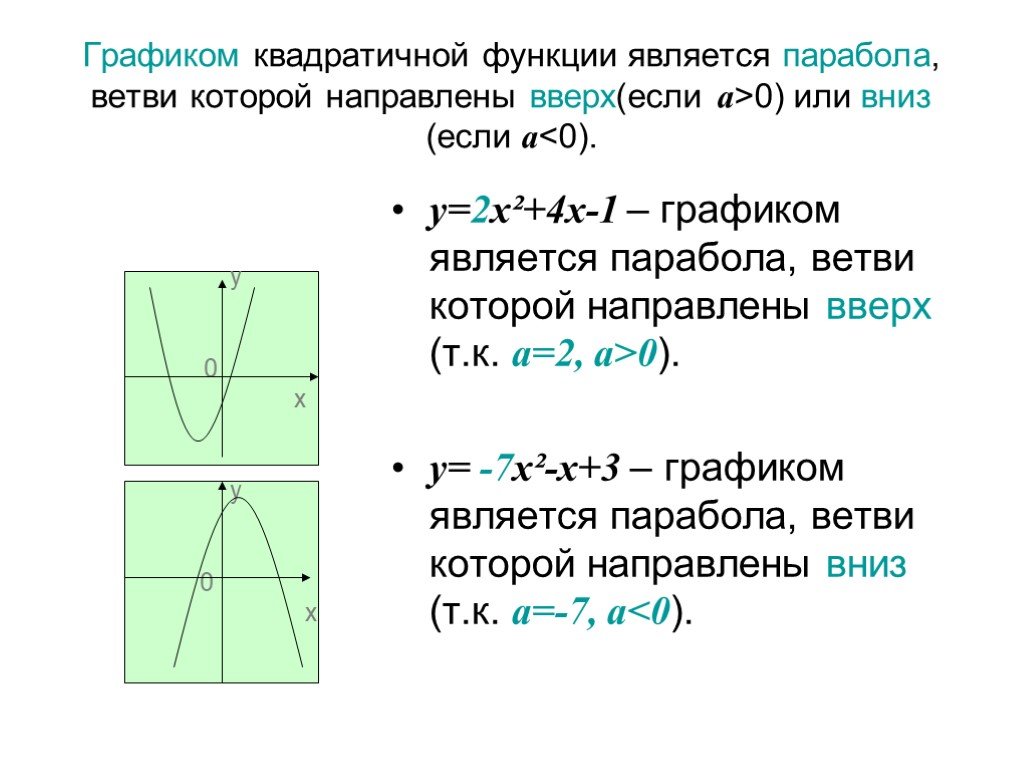
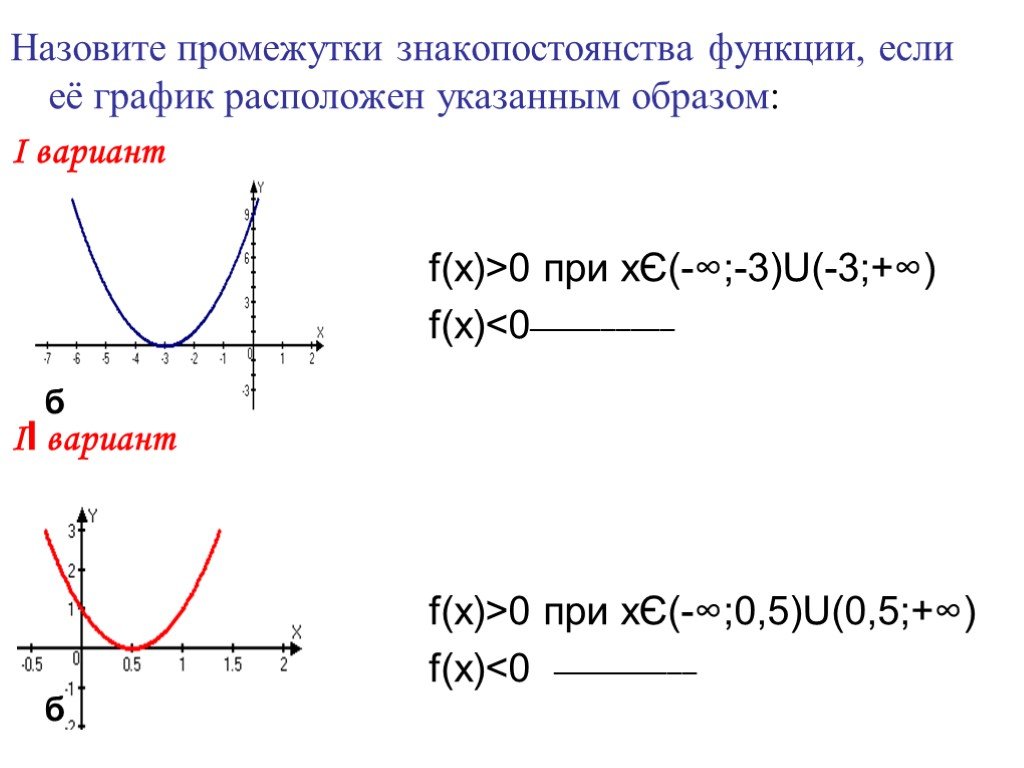
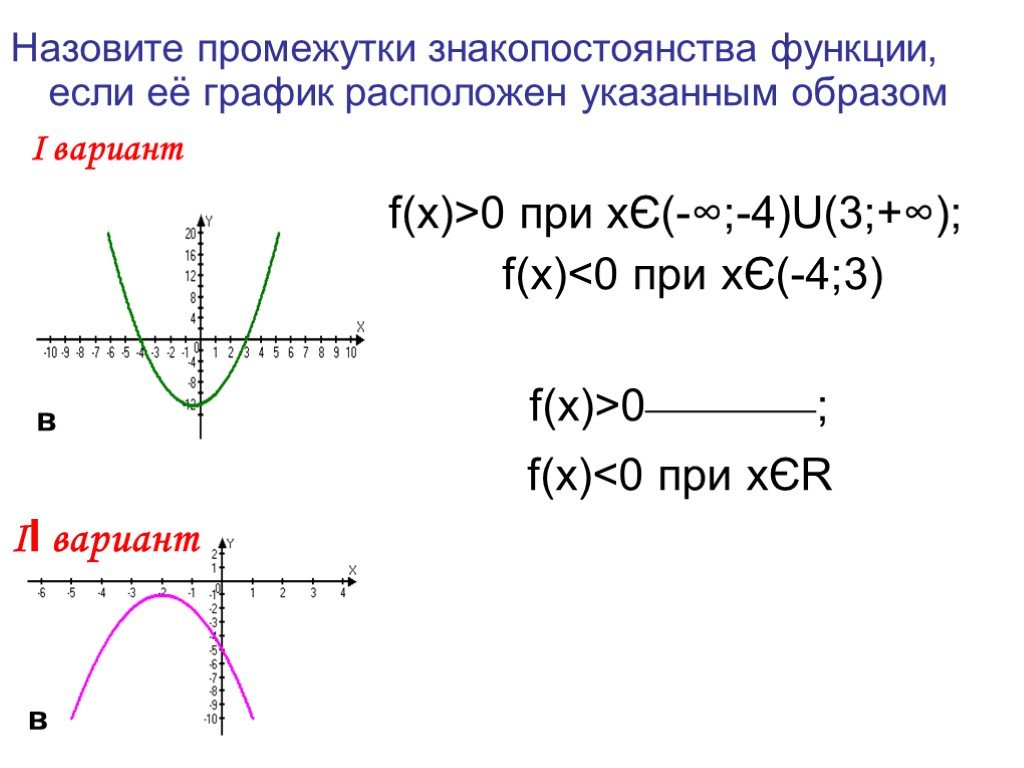
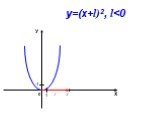
1)направление «ветвей» параболы. если а>0, то «ветви» параболы направлены вверх; если а 0 - «ветви» параболы направлены вверх;. 2)Нахождение координат ...Преобразование графика квадратичной функции
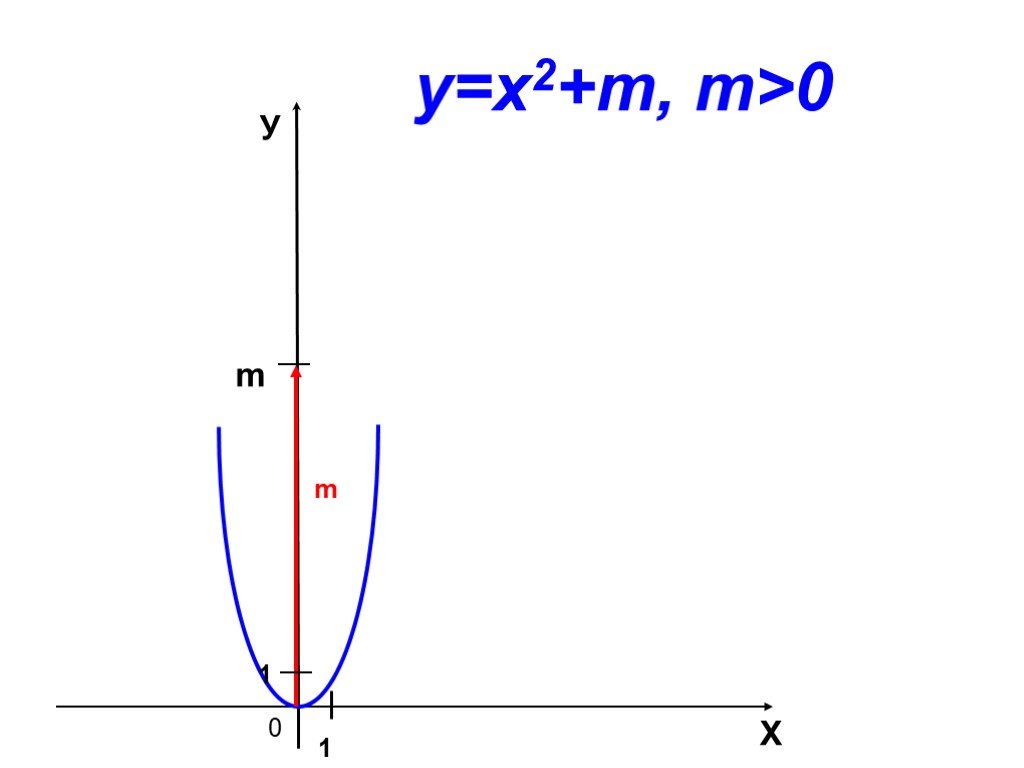
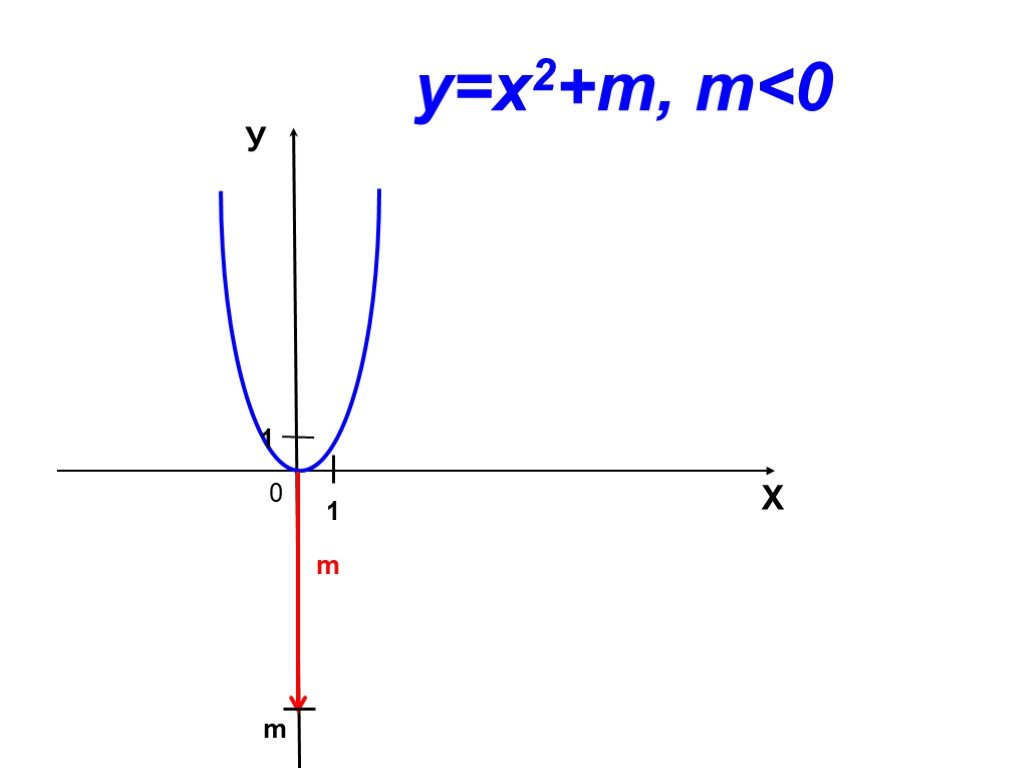
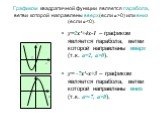
Проверка результатов исследований. 1 группа (y=x2+c) y=x2+3;. С=3 – сдвиг вверх по оси ординат на 3. 2 группа (y=x2+c) y=x2-5;. С=-5 – сдвиг вниз ...Преобразования графиков квадратичной функции
Квадратичной функцией называется функция вида у = ax²±bx±c Например : у=2x²+3x-4, а=2, b=3,c=-4 Графиком квадратичной функции является парабола Для ...Функции. Графики функций
1. Задайте формулой функцию, сопоставляющую каждому числу третью степень этого числа. 2. Функция задана формулой Найдите её значение при х = 2. 3. ...Построение графика квадратичной функции
Цели:. Формирование у учащихся умения строить график квадратичной функции в соответствии со схемой. определение. Квадратичной функцией называется ...Графики и функции в основной школе
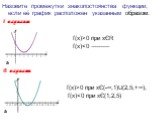
Постройте график функции. и найдите все значения а, при которых прямая у=а имеет с графиком данной функции ровно одну общую точку. 1. О чем говорится ...Применение свойств квадратичной функции
Задачи на определение числа корней квадратного уравнения. П р и м е р 1. Имеет ли корни уравнение 1716х2 – 5321х + 3248 = 0? Решение. D = 53212 – ...Свойства и график квадратичной функции
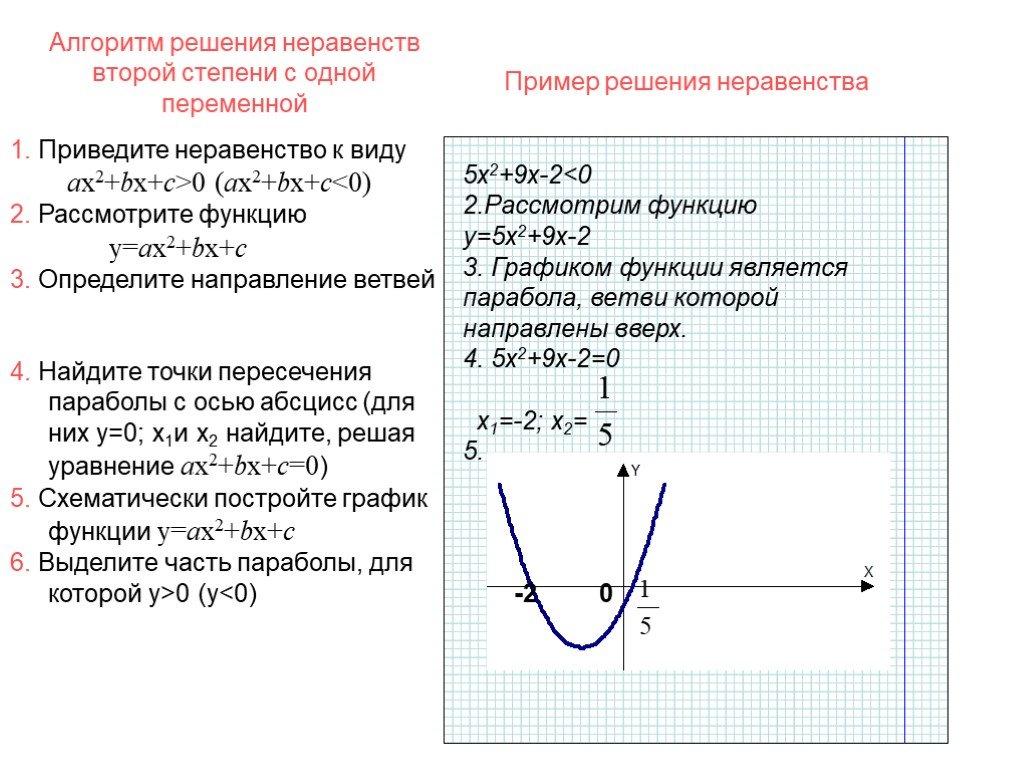
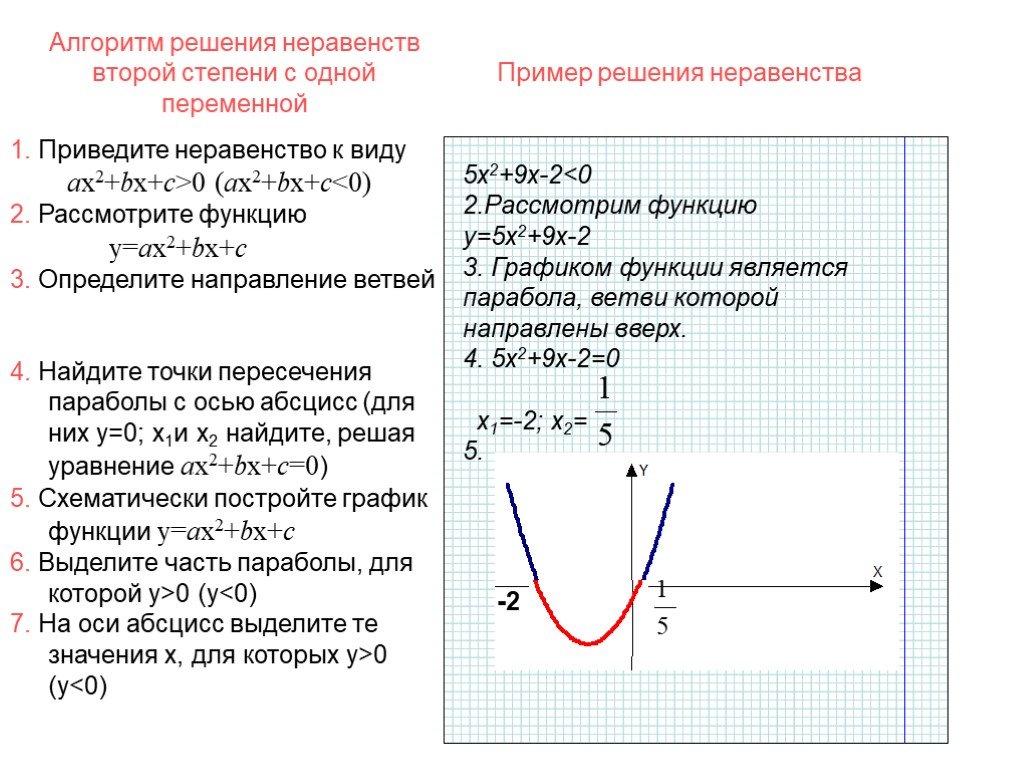
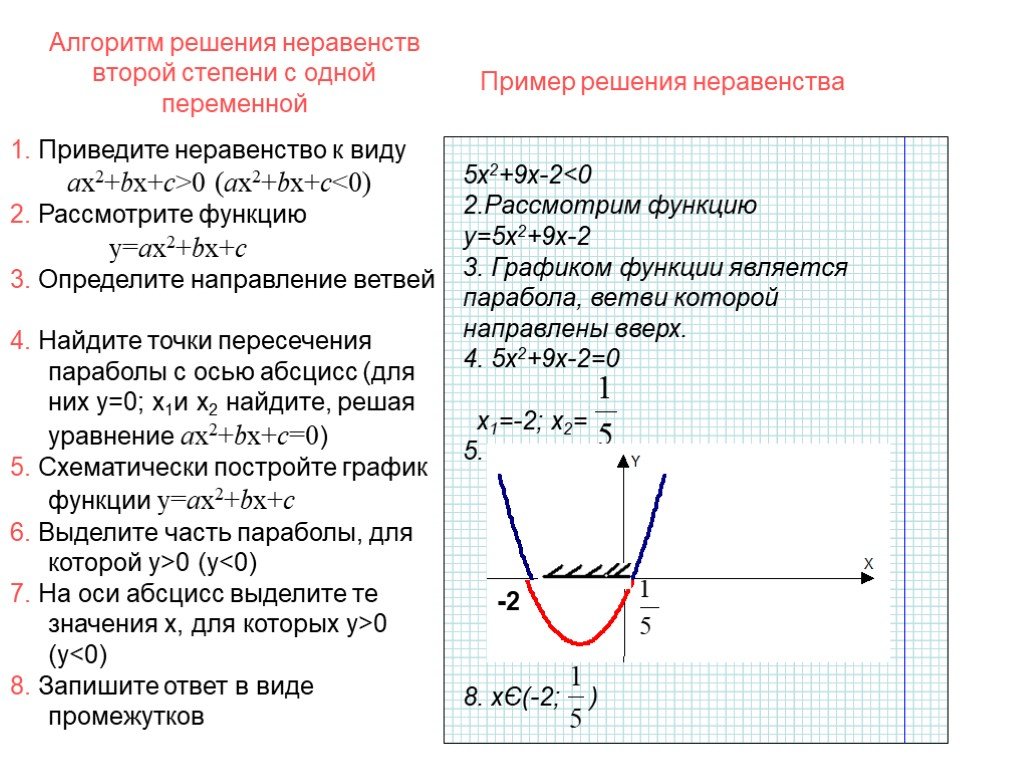
Цели:. вспомнить свойства квадратичной функции вспомнить алгоритм построения графика квадратичной функции рассмотреть задания, предлагавшиеся на ГИА. ...График квадратичной функции. Неравенства с одной переменной
Квадратичная функция и ее график. Квадратичной функцией называется функция, которую можно задать формулой вида y = ax² + bx + c, где х – независимая ...Построение графика квадратичной функции
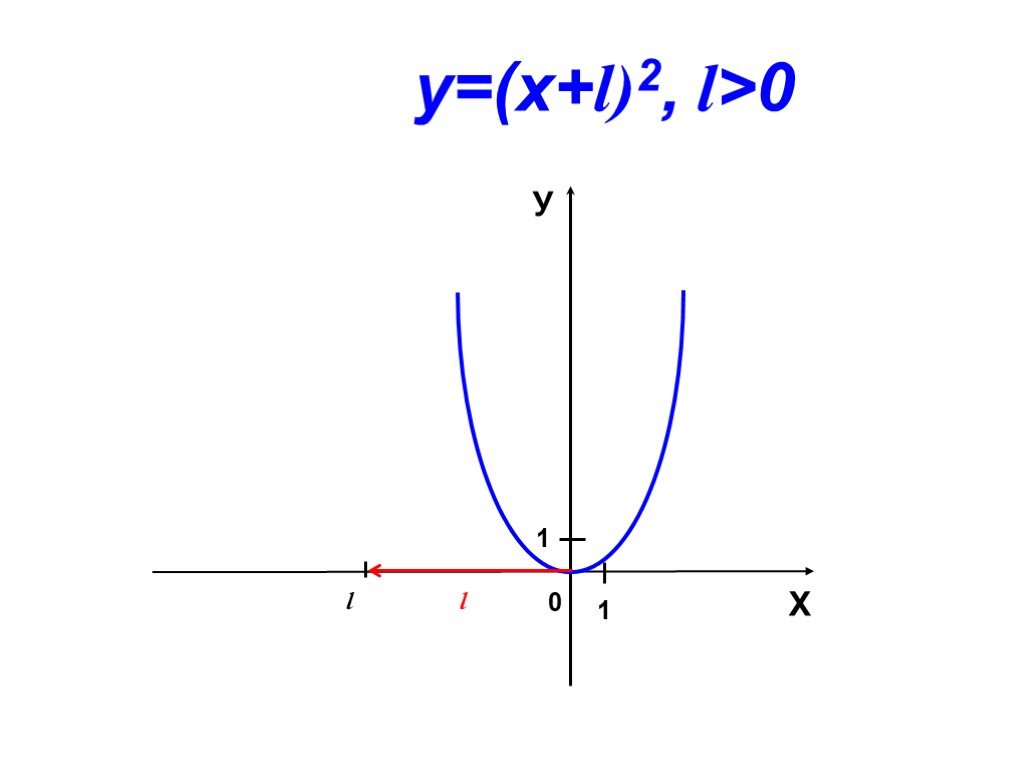
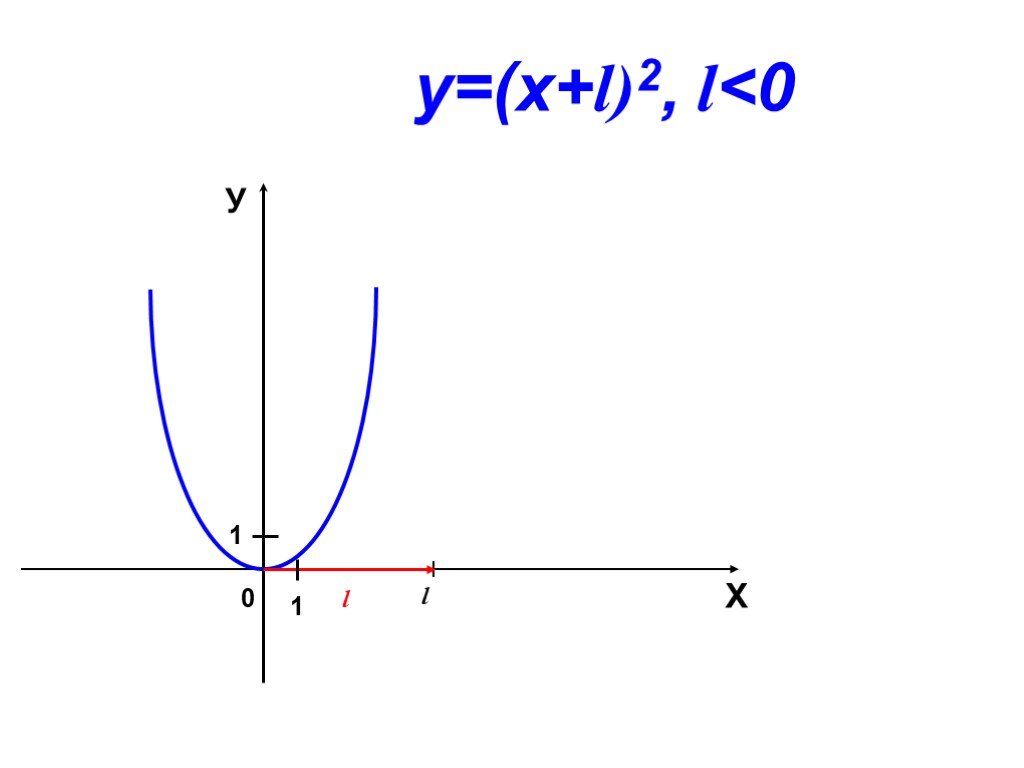
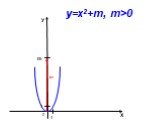
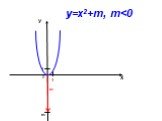
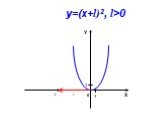
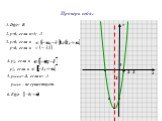
Сдвиг графика функции y = ax2 вдоль оси y. y = x2 y = x2+1 x y. -2 1 0 y = x2 – 2. Сдвиг графика функции y = ax2 вдоль оси x. -3 y = (x+3)2. 2 y = ...График квадратичной функции Неравенства с одной переменной
Квадратичная функция и ее график. Квадратичной функцией называется функция, которую можно задать формулой вида y = ax² + bx + c, где х – независимая ...Урок производная сложной функции
Найдите производные функций:. Найдите угловой коэффициент касательной, проведенной к графику функции. в его точке с абсциссой. Точка движется прямолинейно ...Тригонометрические функции углов в произвольном треугольнике 1-2
Продолжите фразу:. Синусом острого угла прямоугольного треугольника называется. А С В. отношение противолежащего катета к гипотенузе. Косинусом острого ...Степенные функции
“СТЕПЕННЫЕ ФУНКЦИИ” Степенная функция с нечетным натуральным показателем. Корень нечетной степени. Степенная функция с четным натуральным показателем. ...Свойства функции
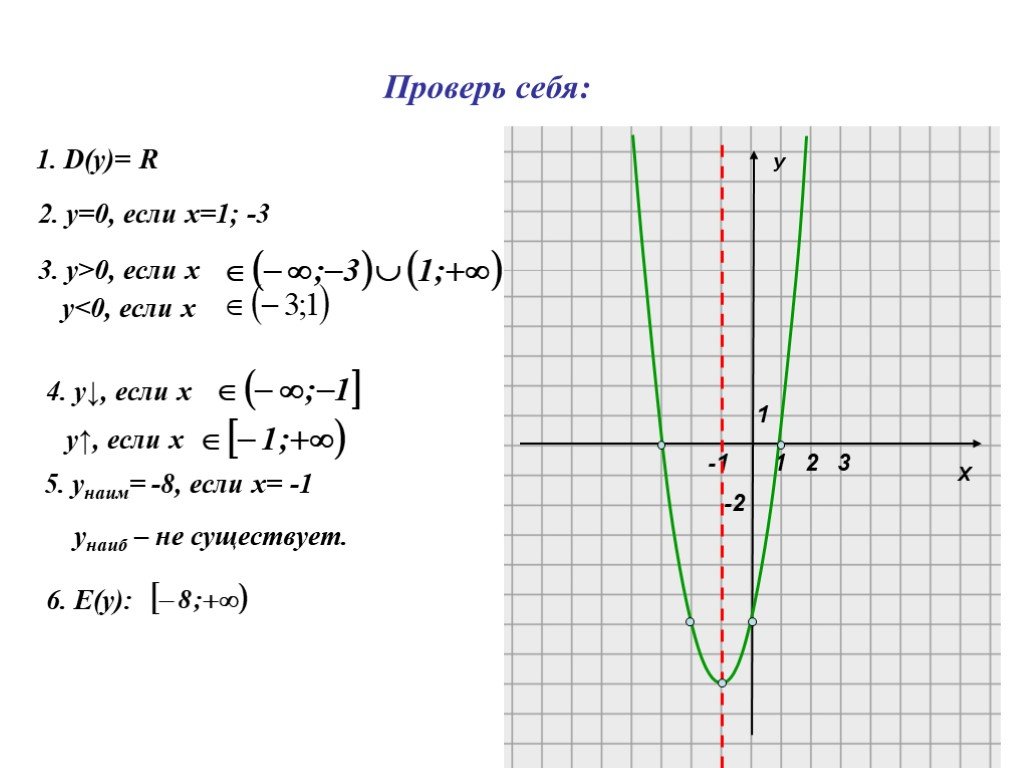
Цель урока:. Расширить представление о функциях; Исследовать функцию и строить график на основе исследования; Продолжать подготовку к ЕГЄ; Показать ...Приращение функции
При сравнении значения функции f в некоторой фиксированной точке x₀ со значениями этой функции в различных точках x, лежащих в окрестности x₀, удобно ...Построение графика линейной функции вида у= kx + b
у = - 2х + 3 – линейная функция. Графиком линейной функции является прямая, для построения прямой нужно иметь две точки. х – независимая переменная, ...График линейной функции
Проверка сплоченности космонавтов. y=x-4 y=-x+4 I вариант II вариант x y 1 2 0 -4 4. Формирование экипажей, посадка в космический корабль. 3 -1 -2 ...Готовимся к ОГЭ – 2018 Задание 23 Графики функций
Цель урока: подготовка к ОГЭ; отработка умений решать задачи, связанные с построением графиков различных функций. Постройте график функции и определите, ...Геометрический смысл производной функции
Рано или поздно всякая правильная математическая идея находит применение в том или ином деле. А.Н.Крылов. Цель урока. 1) выяснить, в чем состоит геометрический ...Конспекты
Построение графика квадратичной функции
План-конспект урока. Тема:. «Построение графика квадратичной функции». Учитель:. Елфимова Н.И. Место работы:. МОУ «СОШ» с.Корткерос. Должность:. ...Элементарные функции и их графики
Методические рекомендации для обучающихся по теме. . «Элементарные функции и их графики». 1. Пропорциональные величины. . Если. ...Построение графика квадратичной функции
Открытый урок по алгебре 8 класс. «Построение графика квадратичной функции». учителя ГОУ центра образования № 671 «Перспектива» Санкт-Петербурга. ...Построение графика квадратичной функции
Урок алгебры в 9 классе. Тема урока: «Построение графика квадратичной функции». Цели урока:. Образовательные. Проверить знания и умения учащихся ...График квадратичной функции и модуль
Администрация города Улан - Удэ. Комитет по образованию. МАОУ «Средняя общеобразовательная школа № 25». Урок алгебры в 9 классе. ...Построение графика квадратичной функции
Учитель: Рогачева Татьяна Викторовна. Место работы: ГОУ СОШ №103, Санкт-Петербург. Должность: Учитель математики. Урок алгебры в 9 классе. . ...Числовые функции их свойства и графики
Технологическая карта урока математики в 9 классе по теме: «Числовые функции их свойства и графики», учебник А.Г.Мордковича. Урок развивающего контроля ...Степенные функции, их свойства и графики
Конспект урока на тему. «Степенные функции, их свойства и графики». Учитель. : Чижова Светлана Анатольевна г. Иваново. Тип урока:. урок формирования ...График квадратичной функции
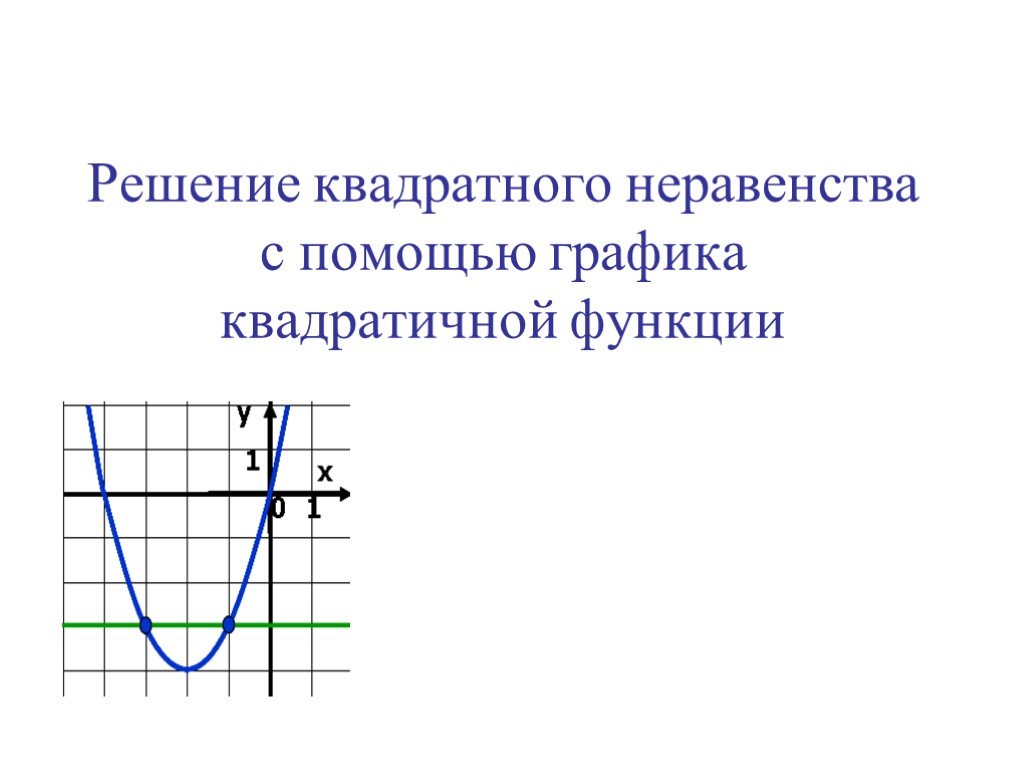
МУНИЦИПАЛЬНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА № 17. КУРГАНИНСКИЙ РАЙОН. Тема: «График квадратичной функции». ...Решение квадратных неравенств с помощью графика квадратичной функции
План конспект урока. Тема:. « Решение квадратных неравенств с помощью графика квадратичной функции». Ф.И.О. Квашнина Мария Андреевна. Место работы: ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:8 октября 2018
Категория:Математика
Содержит:38 слайд(ов)
Поделись с друзьями:
Скачать презентацию