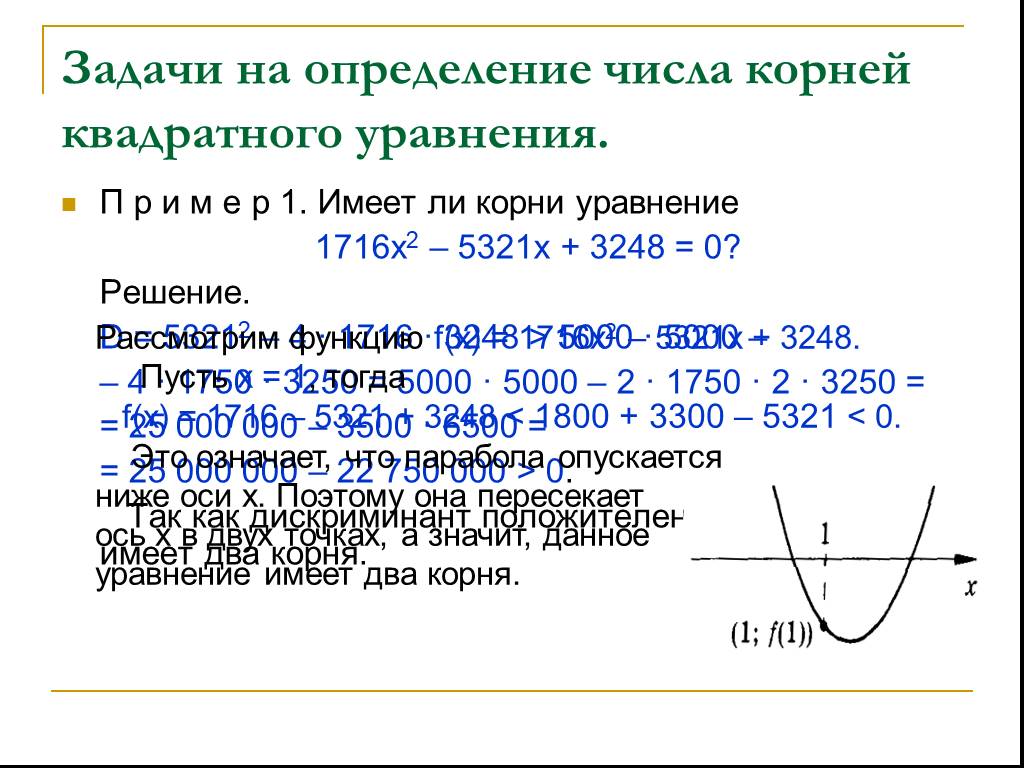
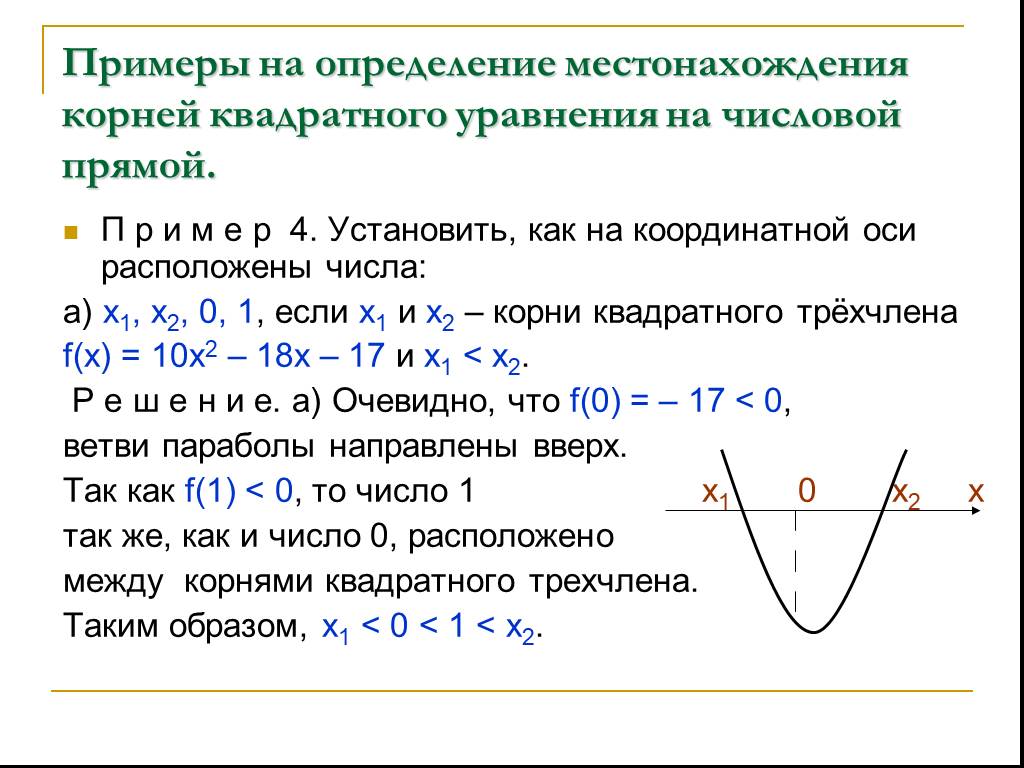
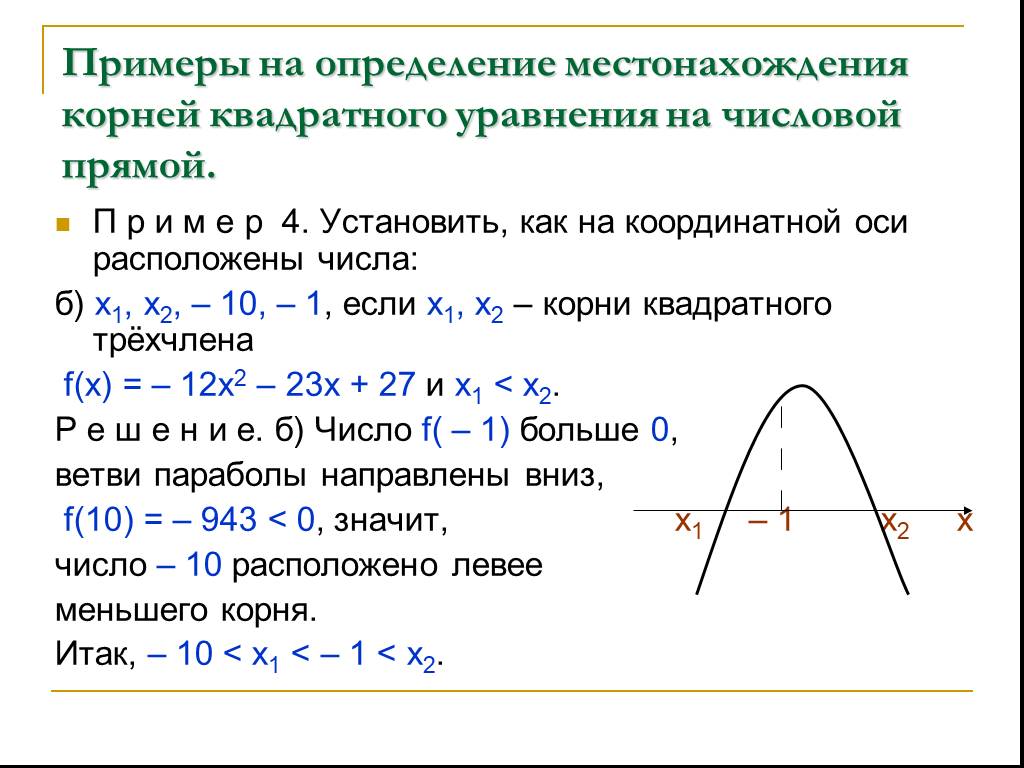
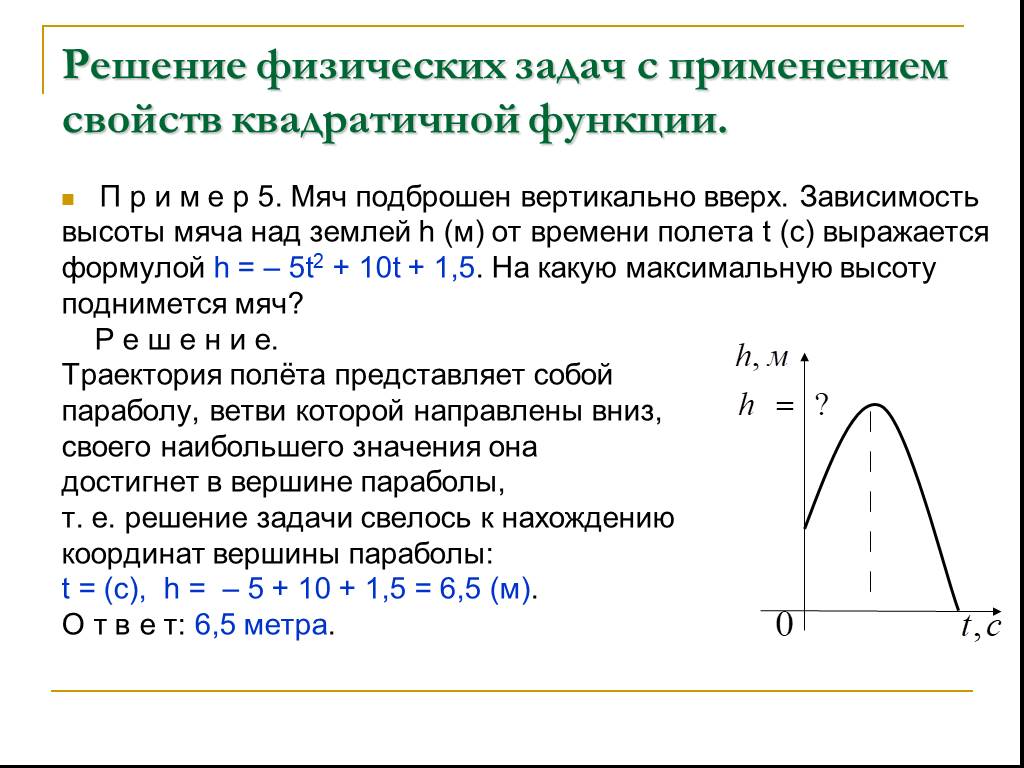
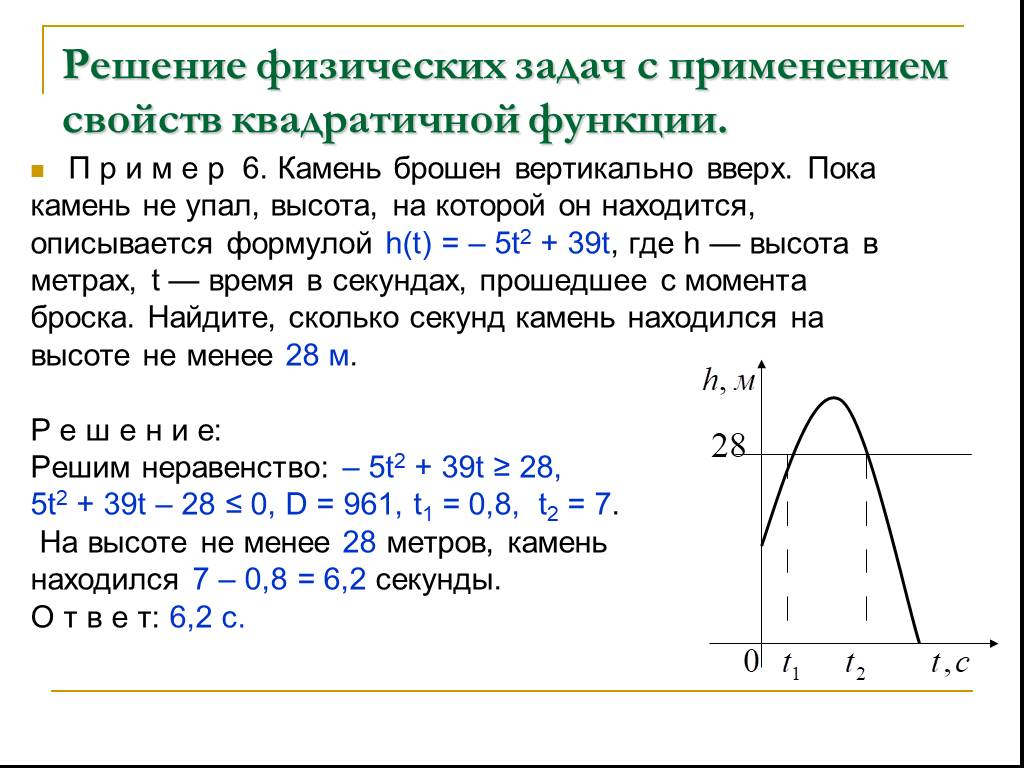
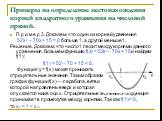
Презентация "Применение свойств квадратичной функции" по математике – проект, доклад
Презентацию на тему "Применение свойств квадратичной функции" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 9 слайд(ов).
Слайды презентации
Список похожих презентаций
Алгоритм построения графика квадратичной функции
1)направление «ветвей» параболы. если а>0, то «ветви» параболы направлены вверх; если а 0 - «ветви» параболы направлены вверх;. 2)Нахождение координат ...Преобразование графика квадратичной функции
Проверка результатов исследований. 1 группа (y=x2+c) y=x2+3;. С=3 – сдвиг вверх по оси ординат на 3. 2 группа (y=x2+c) y=x2-5;. С=-5 – сдвиг вниз ...Преобразования графиков квадратичной функции
Квадратичной функцией называется функция вида у = ax²±bx±c Например : у=2x²+3x-4, а=2, b=3,c=-4 Графиком квадратичной функции является парабола Для ...Графики квадратичной функции
y x 0. График функции y = a x ,. при a=1 при a= -1 1 2 3 4 5 6 -6 -5-4-3-2-1 1 4 9 -9 -4. Преобразование графика квадратичной функции. Построение ...Построение графика квадратичной функции
Цели:. Формирование у учащихся умения строить график квадратичной функции в соответствии со схемой. определение. Квадратичной функцией называется ...Отражение свойств функции в пословицах и поговорках
Цель урока: Изобразить графически как некоторую функцию пословицу и описать свойства функции-пословицы. Возрастающая функция. Функция y=f(x) называется ...Построение графика квадратичной функции
Сдвиг графика функции y = ax2 вдоль оси y. y = x2 y = x2+1 x y. -2 1 0 y = x2 – 2. Сдвиг графика функции y = ax2 вдоль оси x. -3 y = (x+3)2. 2 y = ...График квадратичной функции Неравенства с одной переменной
Квадратичная функция и ее график. Квадратичной функцией называется функция, которую можно задать формулой вида y = ax² + bx + c, где х – независимая ...График квадратичной функции. Неравенства с одной переменной
Квадратичная функция и ее график. Квадратичной функцией называется функция, которую можно задать формулой вида y = ax² + bx + c, где х – независимая ...Построение графика линейной функции вида у= kx + b
у = - 2х + 3 – линейная функция. Графиком линейной функции является прямая, для построения прямой нужно иметь две точки. х – независимая переменная, ...Понятие функции
Содержание:. что такое функция история создания названия функции аналитический способ задания функции табличный способ задания функции способ описания ...Взаимное расположение графиков линейной функции
Разбейте функции, заданные формулами, на группы:. у = 2х - 3; у = х2 - 3; у = - 5х; у = 4 - 0,5х; у = - х +2; у=15х;. 7. 8. 9. 10. у = х (1 - х). ...Определение производной от функции
Определение производной функции (Содержание). Геометрический смысл отношения Геометрический смысл отношения при Геометрический смысл производной функции ...Обратные тригонометрические функции
Историческая справка. Тригонометрические функции возникли впервые в связи с исследованиями в астрономии и геометрии. Соотношения отрезков в треугольнике ...Непрерывность функции
Определение: Функция называется непрерывной в точке , если: функция определена в точке и ее окрестности; существует конечный предел функции в точке ...Логарифмы. Применение логарифмов
повторить определение логарифма; закрепить основные свойства логарифмов; - способствовать формированию умения применять свойства логарифмов при упрощении ...Вычисление производной функции
При вычислении производной функции, будем иметь в виду, что один из способов найти производную - это взять достаточно малые значения справа и слева ...Геометрический смысл производной функции
Рано или поздно всякая правильная математическая идея находит применение в том или ином деле. А.Н.Крылов. Цель урока. 1) выяснить, в чем состоит геометрический ...Выделение элементов и свойств геометрических фигур
Геометрические фигуры являются эталонами, пользуясь которыми человек определяет форму предметов и их частей. Проблему знакомства детей с геометрическими ...Возрастание и убывание функции
Числовые промежутки. [α;b] – отрезок (α;b) – интервал (α;b] – полуинтервал [α;b) - полуинтервал. Функция f(x) называется возрастающей на некотором ...Конспекты
Применение параллельного переноса при построении квадратичной функции
Урок по теме. : «Применение параллельного переноса при построении квадратичной функции». Тип урок. а: урок повторения. Цель урока:. Повторить ...Применение производной к исследованию свойств функции и к решению прикладных задач
Конспект урока алгебры для учащихся 10 класса. Тема урока:. Применение производной к исследованию свойств функции и к решению прикладных задач. ...Применение свойств рациональных чисел для рационализации вычислений
Тема: Применение свойств рациональных чисел для рационализации вычислений. Тип урока:. Формирование умений и навыков. Цели урока:. Обучающие:. ...Производная. Геометрический смысл производной. Применение производной к исследованию функции. Задачи В-8
Государственное общеобразовательное учреждение. Гимназия №205. Урок по теме. « Производная. Геометрический смысл производной. Применение ...Применение свойства монотонности функций при решении уравнений и неравенств
Тамбовское областное государственное автономное образовательное учреждение – общеобразовательная школа – интернат. . «Мичуринский лицей». ...Применение свойств арифметического квадратного корня
Урок математики по теме: "Применение свойств арифметического квадратного корня" (8-й класс). . Аксютченко. . Жанна Владимировна,. учитель математики. ...Применение свойств квадратных корней
Урок по алгебре в 8 классе. Учитель:. Патрина Татьяна Николаевна, МОУ СОШ №120 с углубленным изучением отдельных предметов Московского района города ...Применение свойств квадратного корня
План- конспект урока. Применение свойств квадратного корня. (Тема урока). . ФИО (полностью):. . Старикова Валентина Валерьевна. . ...График квадратичной функции и модуль
Администрация города Улан - Удэ. Комитет по образованию. МАОУ «Средняя общеобразовательная школа № 25». Урок алгебры в 9 классе. ...Применение свойств арифметического квадратного корня
ПЛАН-КОНСПЕКТ УРОКА «Применение свойств арифметического квадратного корня». . ФИО (полностью). . . Рыжова Наталья Михайловна. . ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:1 мая 2019
Категория:Математика
Содержит:9 слайд(ов)
Поделись с друзьями:
Скачать презентацию