Презентация "Вероятность появления события" по математике – проект, доклад
Презентацию на тему "Вероятность появления события" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 25 слайд(ов).
Слайды презентации
Список похожих презентаций
Случайные события и вероятность
Определение вероятности. В толковом словаре С.И. Ожегова и Н.Ю. Шведовой: «Вероятность – возможность исполнения, осуществимости чего-нибудь». Основатель ...Случайные события. Вероятность случайного события
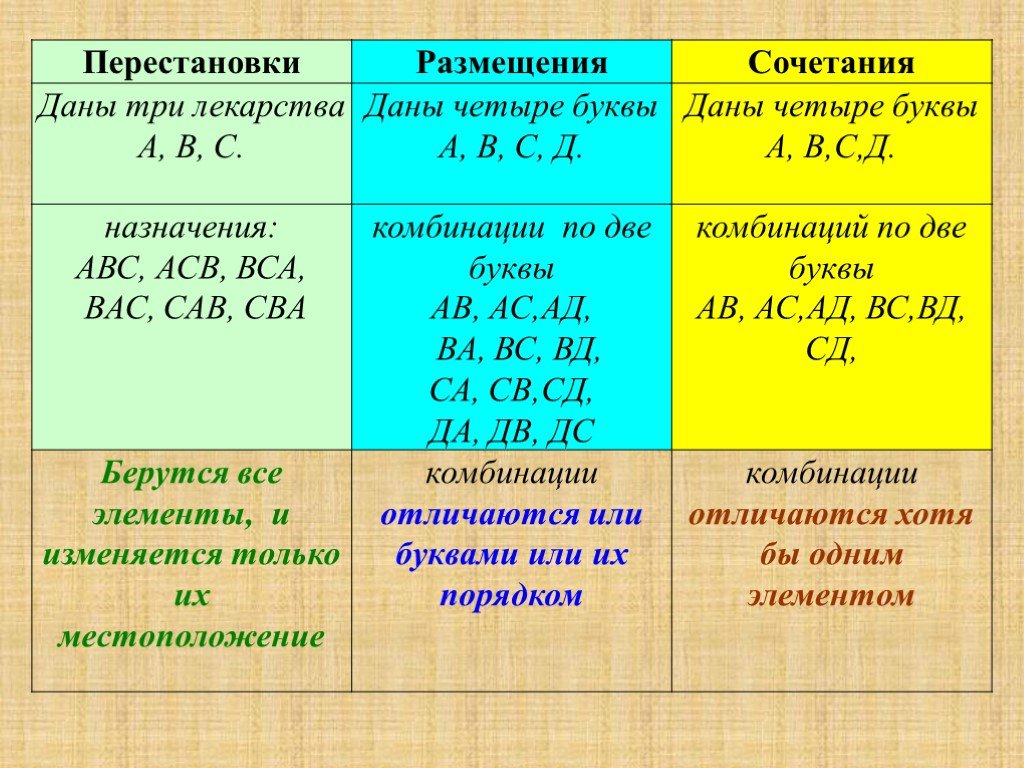
3.9.17 Вспомним. Какими способами мы умеем решать комбинаторные задачи? Таблица вариантов Дерево вариантов Правило умножения. Вспомним формулы для ...Случайное событие. Вероятность события
Теория вероятностей – математическая наука, изучающая закономерности в случайных явлениях. Под опытом (экспериментом, испытанием) мы будем понимать ...Вероятность события
Встречаясь в жизни с различными событиями, мы часто даем оценку степени их достоверности. При этом произносим. Например, такие слова: «Это невероятно» ...Вероятность события
Цели:. Знать понятие вероятности события; виды событий; формулу для вычисления вероятности. Уметь вычислять в простейших случаях вероятности событий. ...Случайные события
Cлучайное событие. Это событие, которое в одних и тех же условиях может произойти, а может и не произойти. Достоверное событие. Это событие, которое ...Относительная частота случайного события
Цели:. усвоить понятия случайного события, относительной частоты случайного события; научиться вычислять относительную частоту случайного события. ...Операция факториалов и история появления его в положительных рядах
Произведение первых натуральных чисел называется n-факториал и обозначается n!; По определению: Чтобы найти факториал числа, необходимо вычислить ...Несовместимые события
Правило сложения вероятностей. Мы знаем, что если событие А и В не имеют благоприятствующих элементарных событий, то они не могут наступить одновременно ...История появления цифр
Арифметика каменного века. Первыми понятиями математики, с которыми столкнулись люди, были «больше» и «столько же». ЦИФРЫ КАМЕННОГО ВЕКА. Древние ...Вероятность и статистика
Цель игры:. Пробудить у учащихся интерес к изучению математики, расширить их кругозор. Объединить элементы наук – теории вероятностей, статистики ...Вероятность и геометрия
Классическая вероятностная схема. Для нахождения вероятности случайного события A при проведении некоторого числа опытов следует: Найти число N всех ...Теория вероятности события
Введение в комбинаторику. В математике существует немало задач, в которых требуется из имеющихся элементов составить различные наборы, подсчитать ...Вероятность выигрыша в лотереях
Цель работы: проверка (эксперементальная) формул комбинаторики для нахождения вероятности случайного события в выигрыше лотереи. Задачи: - определить ...Синус, косинус, тангенс и котангенс, алгебра,
Синус и косинус. Что будем изучать:. Определение синуса и косинуса. Определение тангенса и котангенса. Основное тригонометрическое тождество. Примеры ...Тригонометрические функции углового аргумента - алгебра,
Тригонометрическая функция углового аргумента. Что будем изучать:. Определение. Примеры. Вспомним геометрию. Градусная мера угла. Радианная мера угла. ...Матричная алгебра в экономике
Содержание:. ● Вступление ● Что такое матрицы и операции над ними ● Решение экономических задач матричным методом ● Заключение ● Список используемой ...Реляционная алгебра – механизм манипулирования реляционными данными
Две группы операций РА. теоретико-множественные операции специальные реляционные операции. Теоретико-множественные операции. объединения отношений; ...ГИА 2013. Модуль алгебра №6
ГИА – 2013 г. Модуль «Алгебра» №6. «ГИА-2013. Математика: типовые экзаменационные варианты: 30 вариантов» под редакцией А. Л. Семенова, И. В. Ященко. ...ГИА 2013. Модуль алгебра №8
Модуль «Алгебра» №8. Повторение (4). Решите неравенство 7+2(х-4)≥х+4. Ответ: [-3;+∞). Повторение (подсказка). При решении неравенства можно переносить ...Конспекты
Вероятность случайного события
Конспект урока в 6 классе. . темы «Вероятность случайного события». . . Цель урока:. - развивать воображение, внимание, логическое мышление, ...Расчёт вероятности случайного события
6 класс. Практическая работа № 1. «Расчёт вероятности случайного события». Цель. : научиться рассчитывать вероятность каждого исхода случайного ...Расчёт вероятности случайного события
7 класс. Практическая работа № 1. «Расчёт вероятности случайного события». Цель. : научиться рассчитывать вероятность каждого исхода случайного ...Простые арифметические задачи на определение продолжительности, начала и конца события 7 класс
Простые арифметические задачи на определение продолжительности, начала и конца события. 7 класс. Цели урока:. - Формировать умения решать текстовые ...Вероятность и математическая статистика
Открытый урок. . по учебной дисциплине Теория вероятностей и математическая статистика. Тема: «Вероятность и математическая статистика». Группа ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:23 сентября 2019
Категория:Математика
Содержит:25 слайд(ов)
Поделись с друзьями:
Скачать презентацию