Презентация "Реляционная алгебра – механизм манипулирования реляционными данными" – проект, доклад
Презентацию на тему "Реляционная алгебра – механизм манипулирования реляционными данными" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 42 слайд(ов).
Слайды презентации
Список похожих презентаций
Математика – гимнастика ума.
18 . 3 Н 10 . 6 С 14 . 5 И 13 . 4 У. 60 70 54 52 60. Как зовут моего кота? с и н у. Сколько треугольников? Сосчитай! Часто знает и дошкольник, что ...Матричная алгебра в экономике
Содержание:. ● Вступление ● Что такое матрицы и операции над ними ● Решение экономических задач матричным методом ● Заключение ● Список используемой ...Фракталы – геометрия природы
Задачи:. узнать, что такое «фракталы»; изучить историю возникновения и развития фрактальной геометрии; ознакомиться с биографией создателя фракталов ...Корень n – ой степени. Арифметический корень n – ой степени, его свойства.
Задачи урока:. систематизировать и обобщить знания о корнях; продолжить формирование навыков применения свойств корней при решении задач и для простейших ...Счет и вычисления – основа порядка в голове
Действия с натуральными числами. Редкие и исчезающие животные. Красная книга Российской Федерации (ККРФ) является основным государственным документом, ...Урок – игра «В мире числительных»
"Третий лишний": 1) один, одиночка, одиночество; 2) пятёрка, пятерня, пять; 3) четырёхугольник, четыре, четвёрка. Один Пять Четыре. – Почему вы назвали ...В моде – геометрия
Мода 60 – ых, и поп - арт. Наряды с геометрическими формами смотрятся очень остро. В моде 1920-х годов большое влияние оказало авангардное искусство-от ...Полет – это математика
РАЗМИНКА. Какие числа называются натуральными? Назовите по порядку первые четыре разряда, стоящие в десятичной дроби после запятой. По какому правилу ...Архимед (287 – 212 до н.э.)
Вдруг искупаться я решил И ванну полную налил, Я сел в неё и вот беда, Из ванны вылилась вода. Пришла идея мне тогда, И “Эврика! – воскликнул я”. ...Быстрый счёт – легко и просто
Цели: изучить быстрый счёт с использованием нестандартных приёмов устного счёта, познакомить с упрощёнными приёмами устных вычислений, когда вычисляющий ...Арифметика Л.Ф. Магницкого – «врата учёности» М.В. Ломоносова
М.В. Ломоносов (1711-1765), великий русский учёный, основатель Московского университета. Математику уже затем учить надо, что она ум в порядок приводит. ...«Функции» алгебра
Производная. Производной функции f в точке х0 называется число, к которому стремится разностное отношение при Δх, стремящемся к нулю. Правила дифференцирования. ...«Математика» – новый учебник математики
«Математика» – новый учебник математики. Образовательная система «Школа 2100». Цель Принципы Технология. Авторы Образовательной системы Школа 2100. ...Наша школа – теплый дом
Адаптивная школа для ВСЕХ: для талантливых детей; для обучающихся параллельно в других учебных заведениях; для имеющих пробелы в знаниях; для нуждающихся ...Векторная алгебра
Векторы. Определение. Вектором назовём направленный отрезок, т.е. отрезок прямой, ограниченный двумя точками, одна из которых называется начальной, ...Пирамида – тип многогранников
Исторические сведения о пирамиде. Египетские пирамиды – одно из семи чудес света. Что же такое пирамиды? Усыпальницы египетских фараонов. Крупнейшие ...ВЕЛИЧИНЫ. ЕДИНИЦА ДЛИНЫ – КИЛОМЕТР
60 :2 8 75 15 64 4 :4 *7 +19 :5 *4 56 :15. 20*6=120 (см2) – площадь большого прямоугольника; 13*2=26 (см2) – площадь маленького прямоугольника; 120-26=94 ...Синус, косинус, тангенс и котангенс, алгебра,
Синус и косинус. Что будем изучать:. Определение синуса и косинуса. Определение тангенса и котангенса. Основное тригонометрическое тождество. Примеры ...Весёлая таблица умножения (числа 1 – 4)
Что такое умножение? Это умное сложение. Ведь умней – умножить раз, Чем слагать всё целый час. Умножения Таблица Всем нам в жизни пригодится. И недаром ...Тригонометрические функции углового аргумента - алгебра,
Тригонометрическая функция углового аргумента. Что будем изучать:. Определение. Примеры. Вспомним геометрию. Градусная мера угла. Радианная мера угла. ...Конспекты
Чудо – числа
Конспект урока. ФИО аттестуемого учителя. Арискина Маргарита Адольфовна. . Место работы (наименование учреждения). . МБОУ «Средняя ...Приём вычислений для случая вида 30 – 7
Организационная информация. . . Авторы урока (ФИО, должность). . Шипицына Виктория Васильевна, учитель начальных классов. . . Образовательное ...Урок математики в 3классе: Табличное умножение и соответствующие случаи деления – закрепление. Решение задач, нахождение р прямоугольника
Тема. : Табличное умножение и соответствующие случаи деления – закрепление. Решение задач, нахождение р прямоугольника. . Тип урока. : урок отработки ...Числа 1 – 4. Состав числа 4. Сложение и вычитание в пределах 4
Муниципальное бюджетное общеобразовательное учреждение. «Фатежская средняя общеобразовательная школа №1». Фатежского района Курской области. ...Семья – ячейка общества
План-конспект интегрированного. урока по математике и обществознанию. Класс. : 6 «б». Тема. : «Семья – ячейка общества», «Уравнение». Тип ...Сопоставление согласных звуков по твёрдости – мягкости. Составление и решение задач. Измерение расстояния между точками одного цвета
МБОУ «Средняя общеобразовательная школа №26. с углубленным изучением отдельных предметов». . Нижнекамского муниципального района Республики Татарстан. ...Единицы времени – век
Конспект урока. Учитель: Чащина Ирина Владимировна. Предмет:. математика Класс:. 4. Тема урока:. «Единицы времени – век». Цель:. познакомить ...Прямоугольник – решение задач
Технологическая карта урока. . Предмет, класс. Геометрия, 8 класс. . Авторы УМК. . А.В.Погорелов. . ФИО учителя, школа. . Фёдорова ...Единица времени – неделя
Конспект урока математики в 3 классе. Тема:. «Единица времени – неделя». Цели:. . . 1. Познакомить учащихся с новой единицей измерения времени ...ЕДИНИЦА МАССЫ – КИЛОГРАММ
Урок. математики.Тема. : ЕДИНИЦА МАССЫ –. Килограмм. Педагогическая цель:. . 1. Создать условия для формирования понятия килограмм – как единицы ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:19 июня 2019
Категория:Математика
Содержит:42 слайд(ов)
Поделись с друзьями:
Скачать презентацию
























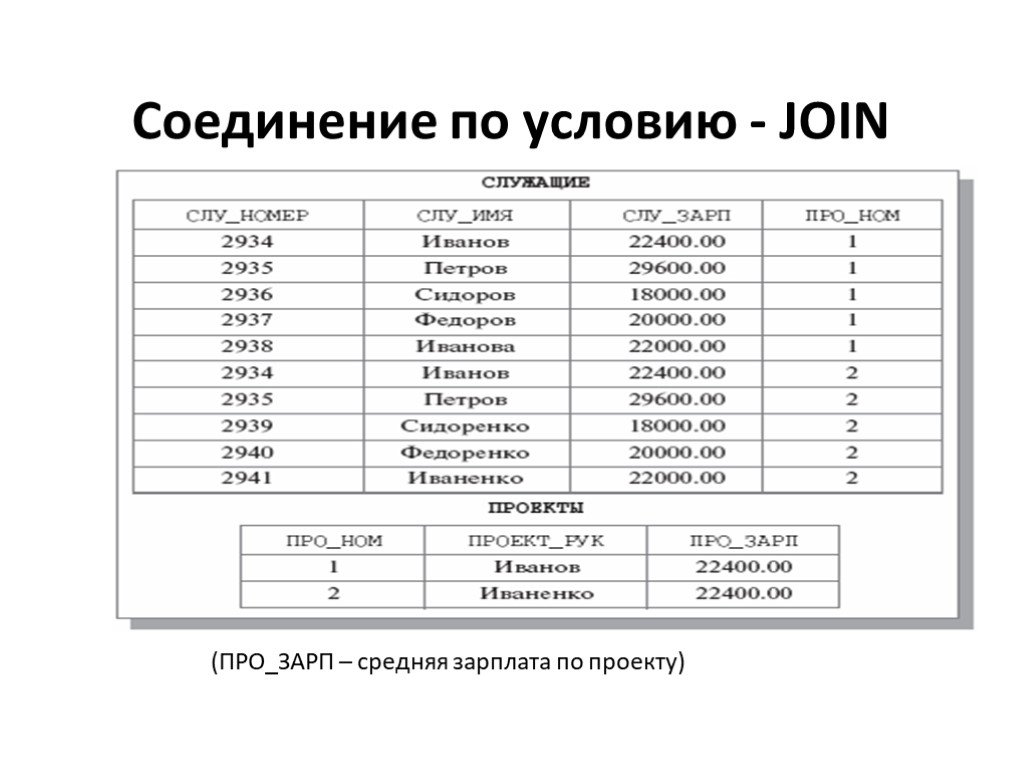
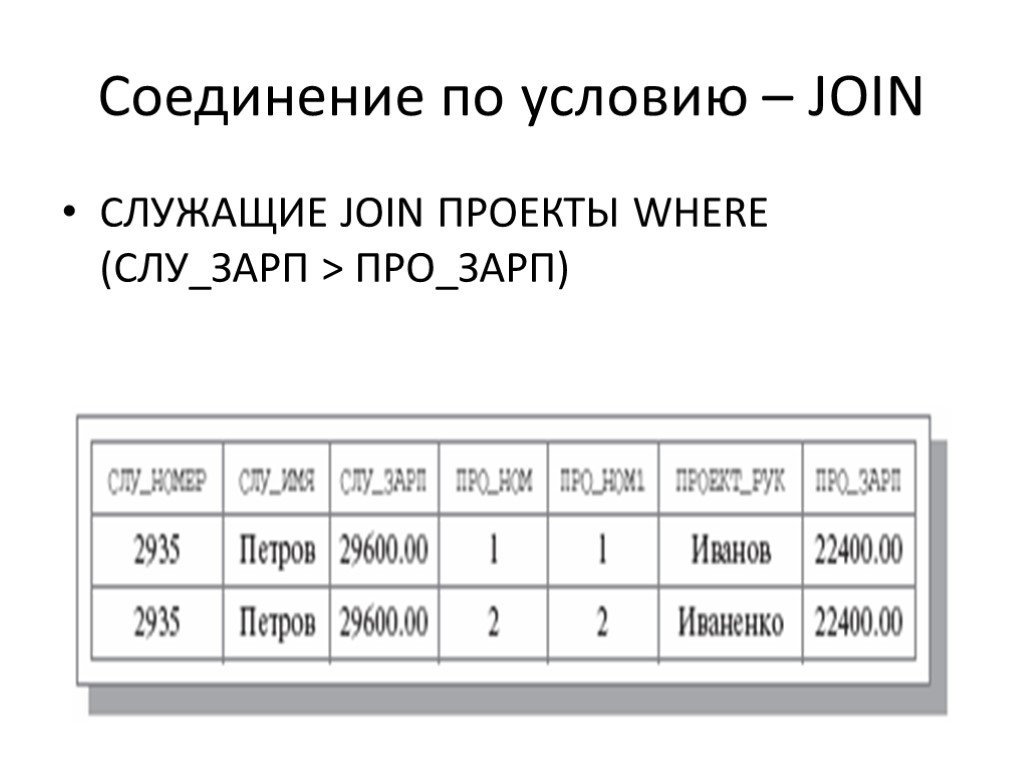

























![Декартово произведение times. Заголовок R1 × R2 R (a1, a2, …, an, b1, b2, …, bm), Тело R1 × R2 ={ra1, ra2, …, ran, rb1, rb2, …, rbm : ra1, ra2, …, ranR1, rb1, rb2, …, rbm R2}. Мощность [R1 × R2 ]= [R1] × [R2] На основе ДК производится операция соединения Декартово произведение times. Заголовок R1 × R2 R (a1, a2, …, an, b1, b2, …, bm), Тело R1 × R2 ={ra1, ra2, …, ran, rb1, rb2, …, rbm : ra1, ra2, …, ranR1, rb1, rb2, …, rbm R2}. Мощность [R1 × R2 ]= [R1] × [R2] На основе ДК производится операция соединения](https://prezentacii.org/upload/cloud/19/06/153791/images/thumbs/screen16.jpg)