Презентация "Пирамида – тип многогранников" по математике – проект, доклад
Презентацию на тему "Пирамида – тип многогранников" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 8 слайд(ов).
Слайды презентации
Список похожих презентаций
Счет и вычисления – основа порядка в голове
Действия с натуральными числами. Редкие и исчезающие животные. Красная книга Российской Федерации (ККРФ) является основным государственным документом, ...Решение задач на построение сечений многогранников
№69. N M P R. Найдите периметр сечения, если SВ=8 см, АС=6 см. №70. К М. №71. Р. №78. №79(а). А С В D. №79(б). №81. в) построить сечение через точки ...Сечения многогранников
Задача 1 Ответ. . Задача 2. . Задача 3. . Задача 4. . Задача 5. . ...Построение сечений многогранников
Определение сечения. Секущей плоскостью многогранника назовем любую плоскость, по обе стороны от которой имеются точки данного многогранника. Секущая ...Построение сечений многогранников геометрия
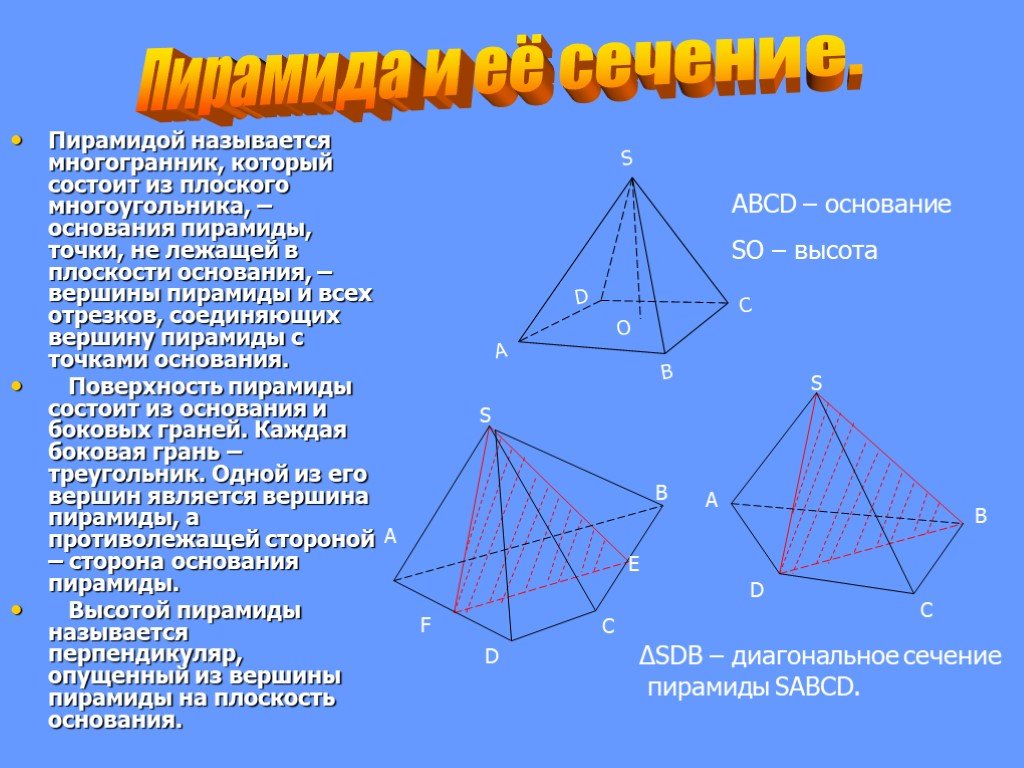
Обучающая цель: формирование умений и навыков построения сечений. Развивающая цель: формирование и развитие у учащихся пространственного представления. ...Пирамида
План. Определение Элементы пирамиды Свойства пирамиды Правильная пирамида Свойства правильной пирамиды Прямоугольная пирамида Поверхность пирамиды ...Платоновы тела – ключ к устройству Земли и Мироздания
Земля, если взглянуть на нее сверху, похожа на мяч, сшитый из двенадцати кусков кожи... Платон, "Федон". Этюд первый. Сферическая сковорода. Представление ...ВЕЛИЧИНЫ. ЕДИНИЦА ДЛИНЫ – КИЛОМЕТР
60 :2 8 75 15 64 4 :4 *7 +19 :5 *4 56 :15. 20*6=120 (см2) – площадь большого прямоугольника; 13*2=26 (см2) – площадь маленького прямоугольника; 120-26=94 ...Весёлая таблица умножения (числа 1 – 4)
Что такое умножение? Это умное сложение. Ведь умней – умножить раз, Чем слагать всё целый час. Умножения Таблица Всем нам в жизни пригодится. И недаром ...Быстрый счёт – легко и просто
Цели: изучить быстрый счёт с использованием нестандартных приёмов устного счёта, познакомить с упрощёнными приёмами устных вычислений, когда вычисляющий ...В моде – геометрия
Мода 60 – ых, и поп - арт. Наряды с геометрическими формами смотрятся очень остро. В моде 1920-х годов большое влияние оказало авангардное искусство-от ...Архимед (287 – 212 до н.э.)
Вдруг искупаться я решил И ванну полную налил, Я сел в неё и вот беда, Из ванны вылилась вода. Пришла идея мне тогда, И “Эврика! – воскликнул я”. ...Арифметика Л.Ф. Магницкого – «врата учёности» М.В. Ломоносова
М.В. Ломоносов (1711-1765), великий русский учёный, основатель Московского университета. Математику уже затем учить надо, что она ум в порядок приводит. ...Аналитическое задание многогранников
Упражнение 1. Два полупространства задаются неравенствами a1x + b1y + c1z + d1 0, a2x + b2y + c2z + d2 0. Как будет задаваться пересечение этих полупространств? ...Урок – сказка
Расшифруйте слово. 63 – р = 23 у : 12 = 7 6х = 1236 65 + у = 134. О Л Б К. х + 605 = 700 у – 169 = 321 1442 : р = 14. Е Н И. Колобок. Упростите выражение. ...Виды многогранников
Многогранником называется тело, ограниченное конечным числом плоскостей. Поверхность многогранника состоит из конечного числа многоугольников, которые ...Экзаменационная работа по алгебре ГИА – 2010
1.Расположите в порядке возрастания числа 0,0801; 0,08; 0,108;. 0,08; 0,0801; 0,108; 0,108; 0,0801; 0,08; 0,08; 0,108; 0,0801; 0,0801; 0,08; 0,108;. ...Виды многогранников
Геометрия является самым могущественным средством для изощрения наших умственных способностей.Г.Галилей. Многогранником называется тело, ограниченное ...
Пирамида
Что такое пирамида? Первые определения этому понятию давали: Евклид Герон Учебники XIXв. Тейлор Лежандр. Евклид. Телесная фигура, ограниченная плоскостями, ...Виды правильных многогранников
Правильных многогранников вызывающе мало, но этот весьма скромный по численности отряд сумел пробраться в самые глубины различных наук. Л. Кэрролл. ...Конспекты
Числа 1 – 7
. Клюшкина Ольга Викторовна. Учитель начальных классов. МБОУ ООШ №269, г. Снежногорск. УМК «Школа 2100» 1 класс. Урок математики. . Тема:. ...Удивительный мир многогранников
Урок по геометрии в 10 классе. Разработала учитель математики. МОУ «Гимназия им. Горького А.М.»:. Фабер Г.Н. Тема:. «Удивительный мир многогранников». ...Числа 1 – 10
Муниципальное образовательное учреждение. Гремячевская средняя общеобразовательная школа. Урок по математике. . (УМК «Школа России»). ...Сантиметр – единица измерения длины
ПЛАН-КОНСПЕКТ УРОКА Сантиметр – единица измерения длины. . ФИО (полностью). . Грибанова Анна Николаевна. . . . Место работы. ...СЛУЧАИ ВЫЧИТАНИЯ ВИДА: 60 – 24
Тема. : СЛУЧАИ ВЫЧИТАНИЯ ВИДА: 60 – 24. Педагогические задачи:. . рассмотреть прием вычитания в случае вида: 60 – 24; закреплять изученные на предыдущих ...Приём письменного вычитания для случаев вида: 7000 – 456, 57001 – 18032
УМК «Школа России» Математика М. И. Моро. Тема урока:. Приём письменного вычитания для случаев вида: 7000 – 456, 57001 – 18032. Цели урока:. . ...Пространственные понятия: вверху – внизу
Урок по математике 1 класс. Тема: Пространственные понятия: вверху – внизу. Цель: 1. Учить детей определять предметы вверху и внизу. . . ...Единицы времени – век
Конспект урока. Учитель: Чащина Ирина Владимировна. Предмет:. математика Класс:. 4. Тема урока:. «Единицы времени – век». Цель:. познакомить ...Единицы времени – век. Таблица единиц времени
Тема урока: Единицы времени – век. Таблица единиц времени. . . Учитель: Ситдикова Р. А. Класс: 4 класс. Цель урока:. Систематизировать знания ...Единица времени – неделя
Конспект урока математики в 3 классе. Тема:. «Единица времени – неделя». Цели:. . . 1. Познакомить учащихся с новой единицей измерения времени ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:26 сентября 2019
Категория:Математика
Содержит:8 слайд(ов)
Поделись с друзьями:
Скачать презентацию