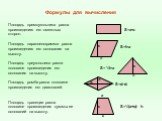
Презентация "Площади по геометрии" – проект, доклад
Презентацию на тему "Площади по геометрии" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 22 слайд(ов).
Слайды презентации
Список похожих презентаций
Викторина по геометрии
Вопрос 1: Выберите верную формулировку определения прямоугольного треугольника:. Вопрос 2: Верно ли, что сумма острых углов прямоугольного треугольника ...Викторина по геометрии
Цель: Воспитание интереса к предмету математики через использование игровых форм. Развитие внимания и сообразительности, логического мышления, формирование ...Вводное повторение курса геометрии о параллельных прямых
Назвать все углы, образовавшиеся при пересечении двух прямых третьей. 1 3 4 5 6 7 8 а в. Задача №1 2 А В Е К. Дано:. Задача № 2 С. Отрезки АВ и СЕ ...«Лабораторные работы по геометрии»
Вписанная и описанная окружности. Цель работы: Проверить при построении в любой ли треугольник можно вписать окружность и вокруг любого ли треугольника ...Вводное повторение курса геометрии
Задача № 1 Доказать: АС = СD. Задача № 2 В Доказать: АD = DС. Задача № 3 Доказать:. Задача № 4. Дано: АD = ЕС Доказать: DBE - равнобедренный. Задача ...Вопросы по геометрии
2 Кто объясняет происхождение термина «геометрия» так: «Геометрия была открыта египтянами и возникла при измерении Земли. Это измерение было им необходимо ...Вводное занятие по геометрии
В мире геометрии. Планиметрия Стереометрия. Сами того не зная, люди все время занимались геометрией. Издавна люди любили украшать себя, свою одежду, ...Вводное повторени для 8 классов по геометрии
8 9 10 11 14 15 16 17 18 30 33 34 35 36 1 3 4 5 6 13 19 31 7. Найти: 440 D С О В А ? 2. Дано:. a0 F b0. O. N R M L. a b c 650. . 450 K E 1350 800. ...Бумажные складные модели и их использование на уроках геометрии в 10 классе
Модель 1 – «Две пересекающиеся плоскости». Согнутый пополам лист бумаги служит моделью двух пересекающихся плоскостей. Линия сгиба – прямая их пересечения. ...Викторина по истории геометрии
Кто из великих геометров древности , по приданию, сказал вражескому солдату, пришедшему его убить: «Не тронь моих кругов»? 1 задание. Ответ 1. Архимед, ...Билеты устного экзамена по геометрии
Прямоугольный треугольник. Треугольник, у которого один из углов прямой, называется прямоугольным. ∆ACB – прямоугольный. Соотношение в прямоугольном ...Анализ учебников по геометрии
Хорошо известно, что успехи в обучении школьников во многом зависят от содержания и структуры учебника, по которому они занимаются. По одним учебникам ...Викторина по математике с ответами
Назовите «математические» растения. Тысячелистник, столетник, золототысячник. Какая геометрическая фигура нужна для наказания детей? Что общего у ...Викторина по математике в 7 классе
14 декабря 2012г. Цели викторины: развивать логическое мышление учащихся; закрепить знания полученные на уроках математики; развивать умение быстро ...Анализ контрольной работы по математике на тему "Натуральные числа и шкалы"
Натуральные числа и шкалы. 5 к л а с с № 1. Цели деятельности учителя. Главная дидактическая цель : организовать деятельность учащихся, направленную ...ГИА-9 по математике
· Наиболее эффективно выстраивать подготовку по тематическому принципу. Не следует стараться решить как можно больше вариантов заданий предыдущих ...ГИА 2012 по математике
Характеристика структуры и содержания экзаменационной работы. Работа состоит из двух частей. Первая часть содержит 18 заданий. Задания части 1 предусматривают ...«Уравнения по математике»
17.10.12. Классная работа. Тема: «Уравнения». Решение уравнений. Математические фокусы. Составление равенств. «Секретная» сказка. «Математику нельзя ...Внеклассное мероприятие по математике в 8 классе.
I. БЛИЦ-ЗНАКОМСТВО. КАЖДОЙ ИЗ КОМАНД БУДЕТ ЗАДАНО ПО 15 ВОПРОСОВ. ЗА КАЖДЫЙ ПРАВИЛЬНЫЙ ОТВЕТ КОМАНДА ПОЛУЧАЕТ 1 БАЛЛ. ВОПРОСЫ ДЛЯ ПЕРВОЙ КОМАНДЫ. ...Башни Кремля. Задачи по математике
Башни Кремля. Спасская башня считается самой красивой и стройной башней. Построена в 1491 году под руководством архитектора Пьетро Антонио Солари ...Конспекты
Как найти часть от целого и целое по его части
Открытый урок по математике в 5б классе. Учитель: Бамбутова М.И. Тема: Как найти часть от целого и целое по его части. Цель: учиться решать задачи ...Из истории геометрии
Урок геометрии в 7 классе «Из истории геометрии». Вовденко Ольга Леонидовна. ,. учитель математики. . МБОУ СОШ № 61 им. М.И. Неделина. . г. ...Итоговое повторение. Решение заданий по теме « Уравнения
Урок по теме. « Итоговое повторение. Решение заданий по теме « Уравнения»». Учитель :. Петрученя Н. В.,. учитель математики. МБОУ «Засосенская ...Методическая разработка урока математики в 5 классе по УМК Г.К. Муравина, О.В. Муравиной
Муниципальное бюджетное общеобразовательное учреждение. средняя общеобразовательная школа № 89. Краснодарского края. Конспект урока ...Вычисление по формулам
Полная разработка открытого урока по математике в 6 классе "Вычисление по формулам". Урок соответсвует ФГОС. Разработка включает в себя конспект урока, ...Конкретно-практическая задача по подбору предмета, равного данному по тяжести
Конспект урока математики в 1 классе по учебнику. . Э.И. Александровой. Тема. : Конкретно-практическая задача по подбору предмета, равного данному ...Космическое путешествие по солнечной системе. Повторение изученного материала
МАТЕМАТИКА. . 4 класс. Тема:. Космическое путешествие по солнечной системе. Повторение изученного материала. Цели:. Повторить материал по ...Закрепление знаний по таблице умножения и деления
Урок математики 3 класс. «Математический цирк». Тема:. Закрепление знаний по таблице умножения и деления. Цель. : Совершенствовать. . вычислительные ...Закрепление изученного материала по разделу «Числа от 1 до 10 включая 0
Министерство образования и науки РТ. Тукаевский муниципальный район. . МОУ «Комсомольская сош ». План урока в 1 классе. ...Закрепление знаний и умений по нумерации в пределах 1000
Открытый урок по математике 3 класс. «Закрепление знаний и умений. . по нумерации в пределах 1000». Цель. : закрепить знания и умения по нумерации ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:23 января 2019
Категория:Математика
Содержит:22 слайд(ов)
Поделись с друзьями:
Скачать презентацию






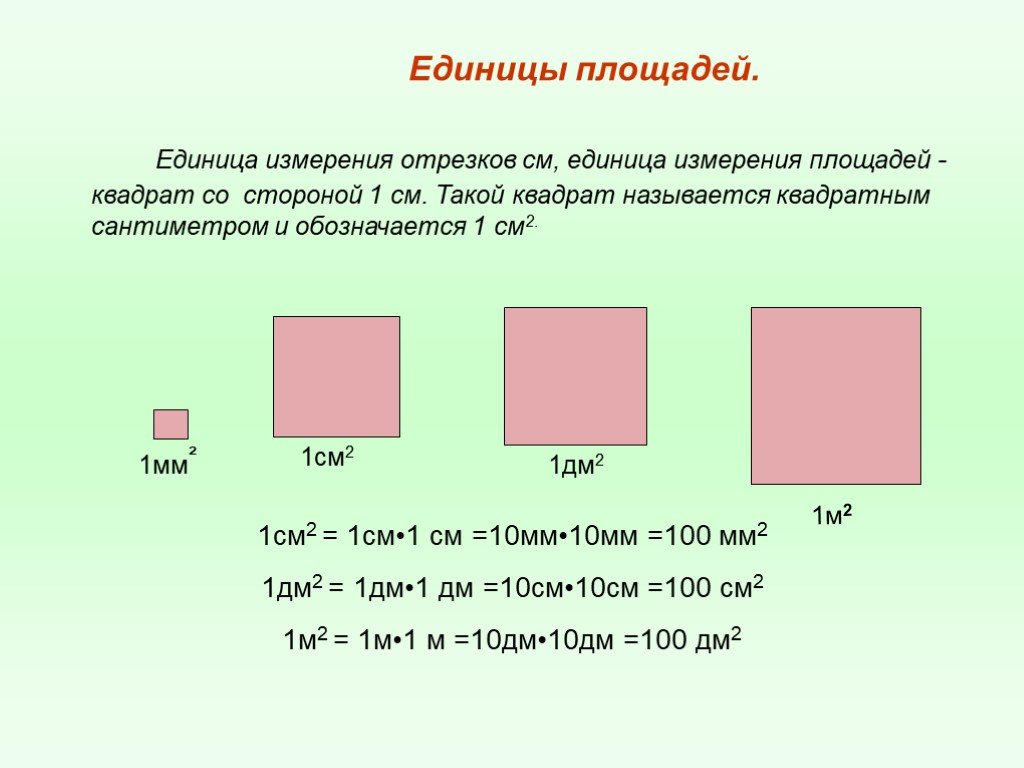





















![Сколько весит площадь? 1.Взять лист плотной бумаги. 2.Взвесить этот лист, получим массу - m [ г ]. 3.Измерить длину и ширину листа; найти площадь S [ см² ]. 4. Разделить массу на площадь; получаем массу 1 см² бумаги, т.е. поверхностную плотность σ [ г / см² ]. 5. Нарисовать на этом же листе любую фи Сколько весит площадь? 1.Взять лист плотной бумаги. 2.Взвесить этот лист, получим массу - m [ г ]. 3.Измерить длину и ширину листа; найти площадь S [ см² ]. 4. Разделить массу на площадь; получаем массу 1 см² бумаги, т.е. поверхностную плотность σ [ г / см² ]. 5. Нарисовать на этом же листе любую фи](https://prezentacii.org/upload/cloud/19/01/119101/images/thumbs/screen11.jpg)