Конспект урока «Прямоугольник – решение задач» по геометрии для 8 класса
Технологическая карта урока
| Геометрия, 8 класс | Авторы УМК | А.В.Погорелов | |
| ФИО учителя, школа | Фёдорова Ирина Юрьевна, МБОУ Серковская СОШ ЩМР | ||
| Тема урока | Прямоугольник – решение задач. (§6, п.54 учебника) | ||
| Тип урока | Урок применения учебной информации (урок – практикум) | ||
| Цель урока: | Применение знаний и умений при решении практических задач, контроль усвоения теоретических знаний. | ||
Структура и ход урока
| Этап урока | Деятельность учителя | Деятельность ученика | УУД | время | |
| | Организационный момент. | Проверяет домашнее задание. Объявляет тему урока. | Сообщают о готовности к уроку и наличии домашнего задания. | Умение осознанно и произвольно строить речевое высказывание в устной форме | 2 мин |
| | Повторение. | Задаёт вопросы, комментирует и корректирует ответы.
| Отвечают на вопросы учителя. | Анализ, построение логической цепи рассуждений | 3 мин |
| | Включение изученной учебной информации в систему известных знаний. | Помогает назвать нужные теоретические факты, правильно сформулировать отдельные шаги решения, предлагает ребятам оценить товарища. | Учащиеся решают задачи:
| Составление и реализация плана, установление причинно - следственных связей, построение логической цепи рассуждений, оценка и коррекция собственной деятельности. | 25 мин |
| | Самостоятельная работа. | Консультирует учащихся при выполнении работы, проверяет правильность выполнения. | Самостоятельно решают №2 из С-2 (Ершова А.П. и др. Самостоятельные и контрольные работы по алгебре и геометрии для 8 класса.), выбрав уровень сложности. | Самодиагностика и коррекция собственных учебных действий, контроль усвоения УИ. | 12 мин |
| | Итог урока. Рефлексия. Домашнее задание. | Предлагает оценить свою работу на уроке. Дает и поясняет домашнее задание. ДЗ: №49, 54 (Дудницин Ю.П. Геометрия. Рабочая тетрадь для 8 класса) | Проводят самооценку, рефлексию. Записывают домашнее задание. | Анализ и синтез, рефлексия способов и условий действия, взаимоконтроль и взаимооценка УПД. | 3 мин |
Саморегуляция учащимися УПД при решении задач
| Помощь учителя | |
| Постановка учебной цели в процессе решения задач: найти способ решения данной задачи | |
| Выявление объективной информации, необходимой для решения задач | Помогает назвать нужные теоретические факты и этапы решения задачи |
| Соотнесение выявленных средств выполнения УПД с собственными знаниями и умениями | Предлагает кратко повторить |
| Деятельность в соответствии с этапами решения задачи | |
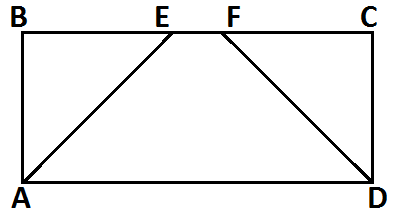
| Работа с текстом и поиск решения задачи №1:
| Предлагает вспомнить свойства смежных углов, теорему о сумме углов треугольника, аксиому измерения углов и использовать данные факты при решении задачи |
| Составление плана решения задачи
| Предлагает одному из учащихся записать решение задачи на доске и остальным проверить решение и оценить товарища |
| Реализация плана решения: выполняется запись решение в тетрадях | Проверяет записи в тетрадях |
| «Взгляд назад» первичное обобщение решения задачи:
| Предлагает в общем виде записать решение |
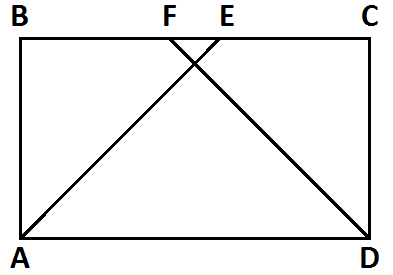
| Решение задачи №2 | Предлагает решить обратную задачу |
| Обобщение решения обеих задач
| Помогает правильно оформить обобщенную схему решения задач |
| Работа с текстом и поиск решения задачи №3:
| Помогает учащимся с построением чертежа
|
| Составление плана решения задачи
| Предлагает одному из учащихся записать решение задачи на доске и остальным проверить решение и оценить товарища |
| Реализация плана решения: выполняется запись решение в тетрадях | Проверяет записи в тетрадях |
| «Взгляд назад» первичное обобщение решения задачи: | Предлагает рассмотреть другой случай |
| Составление плана решения задачи
| Предлагает одному из учащихся записать решение задачи на доске и остальным проверить решение и оценить товарища |
| Реализация плана решения: выполняется запись решение в тетрадях | Проверяет записи в тетрадях |
Технологическая карта урока
| Геометрия, 8 класс | Авторы УМК | А.В.Погорелов | |
| ФИО учителя, школа | Фёдорова Ирина Юрьевна, МБОУ Серковская СОШ ЩМР | ||
| Тема урока | Средняя линия треугольника. (§6, п.58 учебника) | ||
| Тип урока | Урок освоения новой учебной информации (урок – смешанного типа) | ||
| Цель урока: | Познакомиться с новым понятием, изучить свойства этого понятия, попытаться применить изученный материал на практике при решении задач. | ||
Структура и ход урока
| Этап урока | Деятельность учителя | Деятельность ученика | УУД | время | |
| | Организационный момент. | Проверяет домашнее задание. Объявляет и записывает на доске тему урока. | Сообщают о готовности к уроку и наличии домашнего задания. | Умение осознанно и произвольно строить речевое высказывание в устной форме | 2 мин |
| | Повторение. | Задаёт вопросы, комментирует и корректирует ответы.
| Отвечают на вопросы учителя. | Анализ, построение логической цепи рассуждений | 2 мин |
| | Создание проблемной ситуации и формулирование проблемы. | Предлагает прочитать тему урока, познакомиться с опорным конспектом урока (ОКУ) и на основе полученной информации сформулировать возможную цель урока. | Записывают тему урока в тетради, знакомятся с опорным конспектом урока (Приложение 1), формулируют цель урока | Целеполагание, действия постановки и решения проблемы | 3 мин |
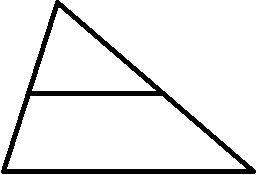
| | Изучение нового материала. | Предлагает учащимся изучить схему понятия и на её основе сформулировать определение средней линии треугольника, сравнить свое определение с определением в учебнике и записать его в тетрадь. | Изучают схему определения понятия, формулируют определение средней линии треугольника, сравнивают свое определение с определением учебника и записывают его в тетради. | Анализ учебной информации, выдвижение гипотез | 7 мин |
| | Первичное закрепление. | Предлагает учащимся
|
| Составление и реализация плана, установление причинно – следственных связей, построение логической цепи рассуждений, доказательство. | 20 мин |
| | Включение изученной учебной информации в систему известных знаний. | Наблюдает за работой учащихся. Помогает, при необходимости проверяет ответы. Комментирует ход решения | Решают у доски задачу № 55 учебника, используя учебник и ОКУ: «Докажите, что середины сторон четырёхугольника являются вершинами параллелограмма». | Контроль и оценка процесса и результатов деятельности, построение логической цепи рассуждений, выбор эффективных способов решения. | 8 мин |
| | Итог урока. Рефлексия. Домашнее задание. | Предлагает оценить свою работу на уроке. Задает и комментирует домашнее задание. ДЗ: №50 – 52(учебник) | Проводят самооценку, рефлексию. Записывают домашнее задание. | Анализ и синтез, рефлексия способов и условий действия, взаимоконтроль и взаимооценка УПД. | 3 мин |
Технологическая карта урока
| Геометрия, 8 класс | Авторы УМК | А.В.Погорелов | |
| ФИО учителя, школа | Фёдорова Ирина Юрьевна, МБОУ Серковская СОШ ЩМР | ||
| Тема урока | Трапеция. Признаки равнобокой трапеции (§6, п.59 учебника) | ||
| Тип урока | Урок освоения новой учебной информации (урок – практикум) | ||
| Цель урока: | Установление истинности утверждений, обратных свойствам равнобокой трапеции | ||
Структура и ход урока
| Этап урока | Деятельность учителя | Деятельность ученика | УУД | время | |
| | Организационный момент. | Проверяет домашнее задание. Объявляет тему урока. | Сообщают о готовности к уроку и наличии домашнего задания. | Умение осознанно и произвольно строить речевое высказывание в устной форме | 2 мин |
| | Повторение. | Задаёт вопросы, комментирует и корректирует ответы.
| Отвечают на вопросы учителя по материалу прошлого урока. | Анализ, построение логической цепи рассуждений | 3 мин |
| | Создание проблемной ситуации и формулирование проблемы. | Предлагает сформулировать утверждения, обратные свойствам равнобокой трапеции и сравнить полученные утверждения с ОКУ. Помогает учащимся сформулировать цель урока. | Под руководством учителя формулируют утверждения, обратные свойствам равнобокой трапеции и цель урока. | Целеполагание, действия постановки и решения проблемы. Анализ учебной информации, выдвижение гипотез. | 3 мин |
| | Изучение нового материала. | Делит учащихся на группы по рядам, распределяет признаки по группам. Предлагает учащимся:
| Работают в группе:
| Структурирование, анализ и поиск учебной информации, установление причинно – следственных связей, выдвижение гипотез и их обоснование. | 10 мин |
| | Первичное закрепление. | Предлагает учащимся записать доказательство полученных утверждений по вариантам (ряд – вариант), проверяет правильность выполнения задания. | 6 учащихся у доски парами по вариантам записывают доказательство полученных утверждений; остальные работают на карточке ОКУ, контролируют и рецензируют ответы у доски (свой вариант). | Построение речевых высказываний, построение логической цепи рассуждений, доказательство, управление поведением партнёра (контроль, коррекция, оценка действий партнёра) | 7 мин |
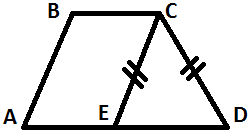
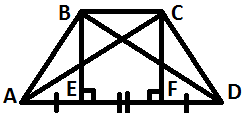
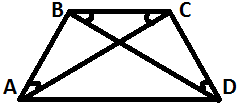
| | Включение изученной учебной информации в систему известных знаний. | Наблюдает за работой учащихся. Помогает, при необходимости проверяет ответы. Комментирует ход решения | Решают у доски задачи по готовым чертежам: «Определите вид трапеции» (Приложение 2) | Контроль и оценка процесса и результатов деятельности, построение логической цепи рассуждений | 15 мин |
| | Итог урока. Рефлексия. Домашнее задание. | Предлагает оценить свою работу на уроке. Дает и поясняет домашнее задание. ДЗ: №97, 98(Дудницин Ю.П. Геометрия. Рабочая тетрадь для 8 класса), заполнить пропуски в карточке ОКУ и выучить теорию. | Проводят самооценку, рефлексию. Записывают домашнее задание. | Анализ и синтез, рефлексия способов и условий действия, взаимоконтроль и взаимооценка УПД. | 5 мин |
Приложение 1
Опорные конспекты
Геометрия 8
Средняя линия треугольника (теория)
Определение: Средней линией треугольника называется ___________
___________________________________________________________.
|
|
Свойство средней линии треугольника: Средняя линия треугольника, соединяющая середины ___________ данных ___________________, __________________________ третьей ________________________ и _____________________ её ________________________.
Д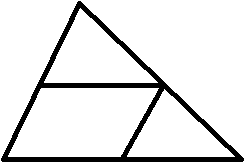
ано: PAC, NCD,
PN – _______________________________ACD.
Доказать: PN _____, PN = AD : 2.
Доказательство:
дополнительное построение: RN _____, RN∩AC=R;
NK – _______________________________ACD, KAD.
| Обоснование | |
| 1. N – ___________________ CD 2. CN = _____ 3. RN _____ 4. R – ___________________ AC 5. P – ___________________ AC 6. P и R совпадают 7. PN _____ 8. NK ____ 9. APNK – ___________________ 10. PN = _____ 11. K – __________________ AD 12. AK =_____ = _______ : 2 13. PN = AD : 2 | по _________________________ средней линии треугольника N – ___________________ CD по _________________________ по теореме __________________ по _________________________ средней линии треугольника по пунктам ___ и ___ по пункту ___ и построению по доказанному по _________________________ параллелограмма по свойству _________________ ____________параллелограмма по _________________________ средней линии треугольника K – __________________ AD по пунктам ___ и ___ |
ч.т.д.
З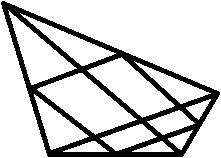
адача №55: Докажите, что середины сторон четырёхугольника являются вершинами параллелограмма.
Дано: _________ – четырёхугольник;
__, __, __, __ – середины ____, ____, ____, ____.
Доказать: ____________ – параллелограмм.
Доказательство:
1) _____ – средняя линия _______ (по _________________________)
_____ – средняя линия _______ (по _________________________)
2) ____ ____ _____ и ______ = _______ = _______ : 2 ( по ________
_____________ средней линии треугольника)
3) ____________ – параллелограмм (по _______________________)
ч.т.д.
Геометрия 8
Признаки равнобокой трапеции (теория)
Определение: Трапеция, у которой _________________________ стороны _________________ называется _______________________________.
1 признак равнобокой трапеции: Если у трапеции углы при основании ___________, то она является _____________________________.
Д
ано: MNEF – _______________________; M = ___;
MF и _____ – __________________.
Доказать: MNEF – _______________________ трапеция
Доказательство:
дополнительное построение: NH _____, NH∩____ = ___.
| Обоснование | |
| 1. NH _____ 2. F = ______ 3. M = ___ 4. M = ______ 5. MNH – ___________________ 6. MN = _____ 7. MF _____ 8. NHFE – __________________ 9. EF =______ 10. ______ = _____ 11. MNEF – __________________ трапеция | по _________________________ по свойству _____________ при ____________________ прямых по _________________________ по пунктам ___ и ___ по _________________________ равнобедренного треугольника по _________________________ равнобедренного треугольника по _________________________ трапеции по _________________________ по свойству _________________ ____________параллелограмма по пунктам ___ и ___ по _________________________ ____________________трапеции |
ч.т.д.
2 признак равнобокой трапеции: Если у трапеции диагонали ____________, то она является _____________________________.
Д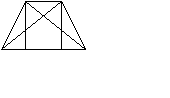
ано: HKPS – _______________________; HP = _____;
HS и _____ – __________________.
Доказать: HKPS – _______________________ трапеция.
Доказательство: дополнительное построение: KMHS, PNHS.
| Обоснование | |
| 1. HS ____ | по __________________________ трапеции |
| 2. KM PN 3. MKPN – ___________________ 4. KM = _____ 5. HP = _____ 6. HPN = _______ 7. PHN = _____ 8. HS – _______________________ 9. PHS = _______ 10. PS = ____ 11. HKPS – ____________________ трапеция | по __________________________ параллельности по __________________________ по свойству __________________ _____________________________ по __________________________ по катету и гипотенузе у равных _____________________ _______________________ равны по __________________________ по ___ признаку у равных _____________________ _______________________ равны по ___________________________ _____________________ трапеции |
ч.т.д.
3 признак равнобокой трапеции: Если у трапеции диагонали являются _______ ______________ острых _______________, то она является _________________.
Дано: EFPS – _______________________;
E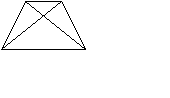
S и _____ – ____________________;
EP – ________________________ _______;
___ – ________________________ _______.
Доказать: EFPS – _______________________ трапеция.
Доказательство:
| Обоснование | |
| 1. ES _____ 2. FPE = _______ PFS = _______ 3. FEP = _______ PSF = _______ 4. _______ = _______ _______ = _______ 5. EFP – ____________________ FPS – ____________________ 6. ______ = FP = ______ 7. EFPS – _____________________ трапеция | по ___________________________ трапеции по свойству _______________ при ______________________ прямых по __________________________ _____________________________ по пунктам ___ и ___ по __________________________ _________________ треугольника по __________________________ равнобедренного треугольника по ___________________________ _____________________ трапеции |
Приложение 2
| 2.
| |
| 3.
| 4.
|
| 5.
| 6.
|
Здесь представлен конспект к уроку на тему «Прямоугольник – решение задач», который Вы можете бесплатно скачать на нашем сайте. Предмет конспекта: Геометрия (8 класс). Также здесь Вы можете найти дополнительные учебные материалы и презентации по данной теме, используя которые, Вы сможете еще больше заинтересовать аудиторию и преподнести еще больше полезной информации.
Список похожих конспектов
Площадь треугольника. Решение задач
геометрия. . 8 класс. . Урок «Площадь треугольника. Решение задач». Оборудование:. 1. ноутбук, проектор. 2. учебники геометрия 7-9 Атанасян. ...
Решение задач на вычисление объема цилиндрических и конических тел
Урок 5. Тема урока:. Решение задач на вычисление объема цилиндрических и конических тел. Тип учебного занятия:. Обобщение и систематизация знаний ...
Четырехугольники. Решение задач
Открытый урок по геометрии в 8 классе. Тема. Четырехугольники. Решение задач. Цели. Усвоение всеми учащимися стандартного минимума и расширение ...
Некоторые свойства прямоугольных треугольников. Решение задач
Тема урока. : «Некоторые свойства прямоугольных треугольников. Решение задач». Цель:. расширить знания учащихся о прямоугольных треугольниках. ...
Теорема Пифагора. Решение задач
Муниципальное общеобразовательное учреждение «Средняя общеобразовательная школа с. Липовка Духовницкого района Саратовской области». Урок ...
Решение задач по теме «Четырехугольники
Урок геометрии в 8 классе по теме. «Решение задач по теме «Четырехугольники»». . Тимофеева Галина Александровна, учитель математики. МБОУ «Средняя ...
Решение задач с помощью теоремы Пифагора
Использование кейс - технологий на уроках математики. Урок геометрии в 8 классе. Тема урока: Решение задач с помощью теоремы Пифагора. Цели ...
Решение задач на применение первого признака равенства треугольников
Дата проведения 21.10.2014 г. Урок геометрии в 7 классе. Тема: «Решение задач на применение первого признака равенства треугольников». Цели урока:. ...
Решение задач на тела вращения
МУНИЦИПАЛЬНОЕ БЮДЖЕТНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ «ГИМНАЗИЯ №40» г. БАРНАУЛА. МЕТОДИЧЕСКАЯ РАЗРАБОТКА УРОКА. «Современные ...
Решение задач на вычисление объемов тел вращения
Конспект урока. Предмет, класс. :. «Геометрия», 11«б» класс. (класс с углубленным изучением математики). Тема. :. «Решение задач на вычисление ...
Решение задач на вычисление площади четырехугольников
Урок по английскому языку по теме:. "Решение задач на вычисление площади четырехугольников". . Цели урока:. Образовательные. :. . -повторить ...
Цилиндр, конус. Решение задач
Муниципальное бюджетное образовательное учреждение. «Гимназия № 7». г. Норильска Красноярского края. Урок математики по ...
Прямоугольные треугольники. Решение задач
Прямоугольные треугольники. Решение задач. Цель:. - обучающая. – знать свойства прямоугольного треугольника, уметь применять эти свойства при ...
Решение задач
Урок геометрии для 7 класса «Решение задач». . Цель:. обзорное повторение материала, изученного за год;. Задачи урока:. проверить усвоение ...
Сфера и шар. Решение задач
Конспект урока по геометрии для учащихся 11 класса. Тема:. «. Сфера и шар. Решение задач. ». Цели:. . - образовательные:. повторить изученный ...
Решение задач на вычисление объема цилиндрических тел
Урок 3. Тема: Решение задач на вычисление объема цилиндрических тел. . Тип учебного занятия:. Урок совершенствования знаний, умений и навыков. ...
Прямоугольник
УРОК ПО ТЕМЕ «Прямоугольник». Цели:. . . Обобщить, систематизировать и углубить имеющиеся знания по теме "Прямоугольник". . Учить логическим ...
Прямоугольник, свойства прямоугольника
Урок геометрии в 8 классе. Тема: «Прямоугольник, свойства прямоугольника». Цели урока. : повторить и закрепить изученный материал о четырехугольниках: ...
Прямоугольник и квадрат
2кл. Тема. : «Прямоугольник и квадрат». Цели:. Сформировать у детей представления о существенных признаках прямоугольника и квадрата, ориентируясь ...