Презентация "Вероятность события" (9 класс) по математике – проект, доклад
Презентацию на тему "Вероятность события" (9 класс) можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 14 слайд(ов).
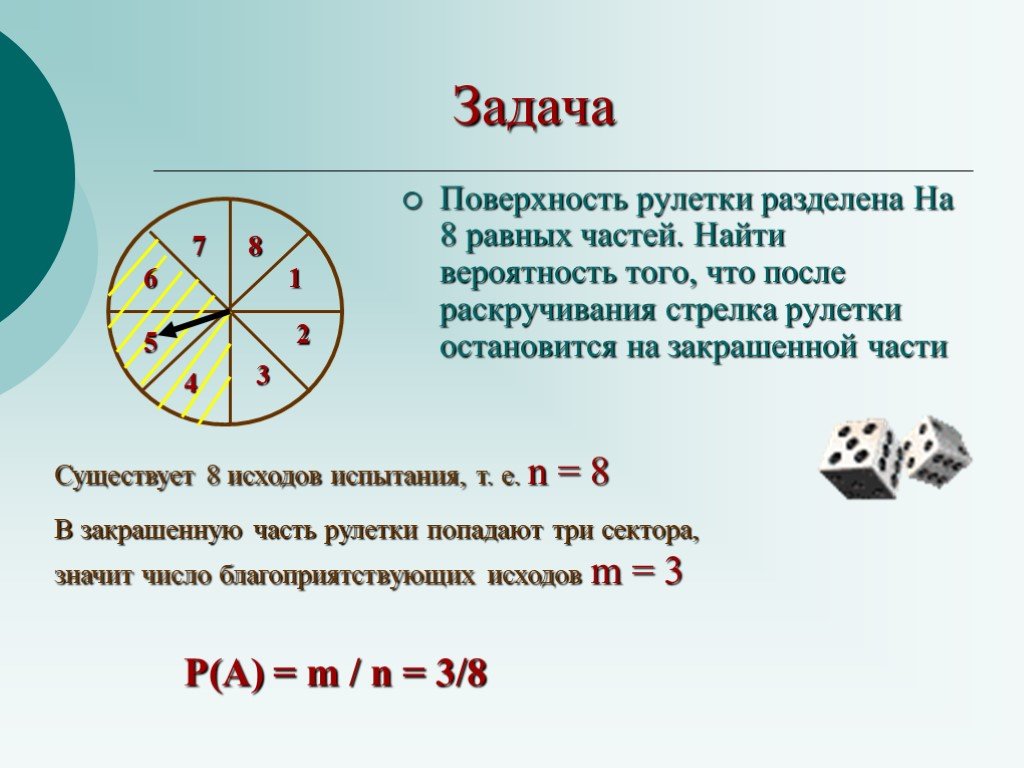
Слайды презентации
Список похожих презентаций
Случайное событие. Вероятность события
Теория вероятностей – математическая наука, изучающая закономерности в случайных явлениях. Под опытом (экспериментом, испытанием) мы будем понимать ...Вероятность события
Цели:. Знать понятие вероятности события; виды событий; формулу для вычисления вероятности. Уметь вычислять в простейших случаях вероятности событий. ...Случайные события и вероятность
Определение вероятности. В толковом словаре С.И. Ожегова и Н.Ю. Шведовой: «Вероятность – возможность исполнения, осуществимости чего-нибудь». Основатель ...Вероятность появления события
Цель урока:. ввести статистическое определение вероятности события, понятие относительной частоты; систематизировать знания учащихся по статистическому ...Случайные события. Вероятность случайного события
3.9.17 Вспомним. Какими способами мы умеем решать комбинаторные задачи? Таблица вариантов Дерево вариантов Правило умножения. Вспомним формулы для ...Случайные события
Cлучайное событие. Это событие, которое в одних и тех же условиях может произойти, а может и не произойти. Достоверное событие. Это событие, которое ...Относительная частота случайного события
Цели:. усвоить понятия случайного события, относительной частоты случайного события; научиться вычислять относительную частоту случайного события. ...Несовместимые события
Правило сложения вероятностей. Мы знаем, что если событие А и В не имеют благоприятствующих элементарных событий, то они не могут наступить одновременно ...Вероятность и статистика
Цель игры:. Пробудить у учащихся интерес к изучению математики, расширить их кругозор. Объединить элементы наук – теории вероятностей, статистики ...Теория вероятности события
Введение в комбинаторику. В математике существует немало задач, в которых требуется из имеющихся элементов составить различные наборы, подсчитать ...Вероятность выигрыша в лотереях
Цель работы: проверка (эксперементальная) формул комбинаторики для нахождения вероятности случайного события в выигрыше лотереи. Задачи: - определить ...Вероятность и геометрия
Классическая вероятностная схема. Для нахождения вероятности случайного события A при проведении некоторого числа опытов следует: Найти число N всех ...Занимательная математика
Хочу стать фокусником…. Искусство отгадывать числа. Есть фокус по отгадыванию чисел: «фокусник» просит вас складывать, умножать, вычитать задуманное ...Занимательная математика
Внеклассное мероприятие по математике. Михаил Юрьевич Лермонтов. Автор: Лазарева Ирина Владимировна Учитель математики, г. Москва, ГБОУ ЦСиО «Самбо-70» ...Занимательная математика
На день какого святого наши предки имели обычай отдавать своих детей в учение? Чтобы ответить на вопрос, выполните действия и составьте слово, расположив ...Занимательная математика
Задачи: Закрепление умений и навыков, полученных на уроках математики. Расширение кругозора учащихся. Привитие интереса к математике. Цели урока: ...Занимательная и информатика и математика для начальной школы
Постановка задачи: Разработка Интернет ресурса, содержащего комплекты иллюстрированных заданий и филвордов. Особенности разработки: 1. Поиск занимательных ...ЕГЭ математика задания В9
Задачи В 9 (ЕГЭ). B9 (№ 25775) Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите V/п. Решение: 1) Находим объём нижнего цилиндра: ...Древнегреческая математика
Понятие древнегреческая математика охватывает достижения грекоязычных математиков, живших в период между VI веком до н. э. и V веком н. э. Начальный ...Конкурсный урок математика
У Ромы не «3», а у Лены не «3» и не «5». Кто какую отметку получил? Проверь себя! 4 5. Запомни! . . Какую из этих схем составила Таня? I способ: 90 ...Конспекты
Вероятность случайного события
Конспект урока в 6 классе. . темы «Вероятность случайного события». . . Цель урока:. - развивать воображение, внимание, логическое мышление, ...Расчёт вероятности случайного события
6 класс. Практическая работа № 1. «Расчёт вероятности случайного события». Цель. : научиться рассчитывать вероятность каждого исхода случайного ...Расчёт вероятности случайного события
7 класс. Практическая работа № 1. «Расчёт вероятности случайного события». Цель. : научиться рассчитывать вероятность каждого исхода случайного ...Простые арифметические задачи на определение продолжительности, начала и конца события 7 класс
Простые арифметические задачи на определение продолжительности, начала и конца события. 7 класс. Цели урока:. - Формировать умения решать текстовые ...Вероятность и математическая статистика
Открытый урок. . по учебной дисциплине Теория вероятностей и математическая статистика. Тема: «Вероятность и математическая статистика». Группа ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:22 августа 2018
Категория:Математика
Классы:
Содержит:14 слайд(ов)
Поделись с друзьями:
Скачать презентацию