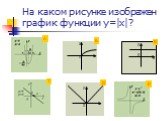
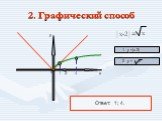
Презентация "Решение уравнений, содержащих модуль" по математике – проект, доклад
Презентацию на тему "Решение уравнений, содержащих модуль" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 15 слайд(ов).
Слайды презентации
Список похожих презентаций
Преобразование графиков функций, содержащих модуль
y = f(x) + a y = f(x) y = f(x) - a +a -a. Преобразование графиков функций. Т1. Параллельный перенос по оси Оу. y = f(x) график исходной функции. y ...Решение диофантовых уравнений
Цели и задачи. Биография Диофанта Диофантовы уравнения с одной неизвестной Диофантовые уравнения первой степени Диофантовые уравнения высших степеней ...Итоговый урок: решение систем уравнений
ЦЕЛИ УРОКА. 1. повторить определения понятий: -система уравнений; -решение систем уравнений; -способы решения систем уравнений. 2. Найти практическое ...Построение графиков функций и уравнений, содержащих переменную под знаком модуля
Тема урока: «Построение графиков функций и уравнений, содержащих переменную под знаком модуля». Тип урока:. «Урок обобщения и систематизации знаний». ...Исследование систем уравнений, содержащих параметр
Графический способ решения. При каких значениях а система уравнений имеет единственное решение? х 2 + y 2 = 169 (x – a)2 + y2 = 4. х2 + у2 = 169 Уравнение ...Ох уж эти показательные… Решение показательных уравнений и неравенств
Ответьте на вопросы. 1. Какая функция называется показательной? 2. Какова область определения показательной функции? 3. Какова область значений показательной ...8 класс "Решение квадратных уравнений"
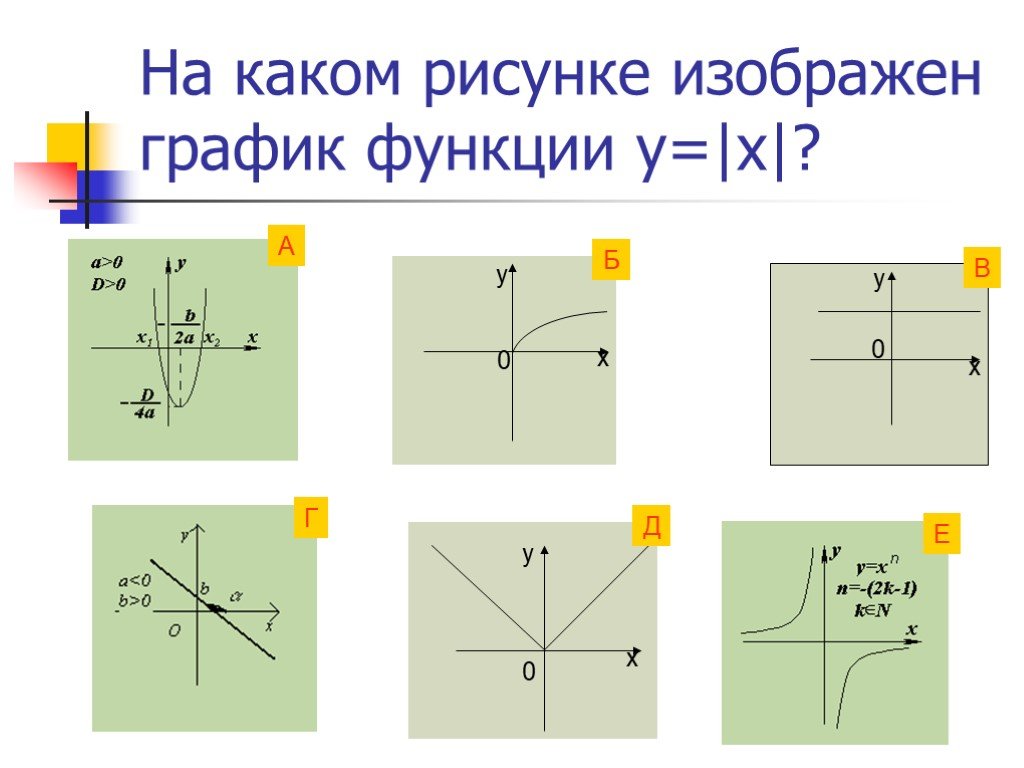
. . . . . . «Уравнение – это золотой ключ, открывающий все математические тайны». . Цель: привести в систему знания о квадратных уравнениях и умение ...Построение графиков функций, содержащих модуль
Цели урока:. Продолжить формирование навыка построения графиков функций, содержащих модуль; обратить внимание на геометрический смысл модуля; Научить ...Графическое решение уравнений
АЛГЕБРА– 7 КЛАСС. ТЕМА: Графическое решение уравнений. Проверка домашнего задания. № 973 № 974. № 976 (а) построить функцию у = х2, построить функцию ...Графическое решение уравнений
Установите соответствие:. А) парабола Б) ветвь параболы С) «галочка» Д) прямая. 4, 6 9 3. х у 0 1 х = 0. х = 0, х = 1. х = -2, 6 0 2 3 4 -2 6. . -2 ...Графическое решение систем уравнений
Лаборатория «ТРУД». Твори, Решай, Учись, Добивайся с интересом и удовольствием! Руководители лаборатории. Начальник лаборатории: Ноумэн Ноу Мэнович ...Графическое решение систем уравнений
Правило решения системы уравнений графическим способом. Построить графики каждого из уравнений системы. Найти координаты точки пересечения построенных ...Графическое решение квадратных уравнений
Немного истории. Еще в древнем Вавилоне могли решить некоторые виды квадратных уравнений. Диофант Александрийский, Аль- Хорезми . Евклид Омар Хайям. ...Графическое решение квадратных уравнений
Цель урока. формировать умение решать квадратные уравнения графическим способом. Решить уравнение х2 – 2х –3 = 0. Решение. I способ Построим график ...Общие методы решения квадратных уравнений
При решении квадратных уравнений часто применяется метод разложения на множители (с помощью вынесения за скобки общего множителя, формул сокращенного ...Аналитические методы решения логарифмических уравнений
Цели урока:. Обобщить и систематизировать изученные методы решения логарифмических уравнений Выявить особенности каждого метода Выяснить, всегда ли ...Решение задач В8 ЕГЭ по математике
Решение. Точки максимума соответствуют точкам смены знака производной с плюса на минус. На отрезке [−9;6] функция имеет две точки максимума x = − 4 ...Методы решения уравнений с одной переменной
Тема урока: «Решение уравнений с одной переменной». Цели урока: закрепить знания и умения решений квадратных уравнений; повторить основные методы ...Решение заданий С2 ЕГЭ-2010
Задача №1:. В прямоугольной системе координат заданы точки O(0;0), D(-5;0), C(0;-12). Найдите площадь боковой поверхности конуса, полученного вращением ...Решение задач в 2-3 действия
Все ль на месте? Всё ль в порядке? Ручки, книжки и тетрадки А линейки и карандаши? Все готовы отвечать? А получать оценку пять? Организационный момент. ...Конспекты
Решение дробных рациональных уравнений
8 класс. Тема « Решение дробных рациональных уравнений». Цель: закрепить изученный материал в ходе выполнения упражнений, развивать навыки решения ...Методы решения уравнений и неравенств, содержащих обратные тригонометрические функции
Конспект урока по алгебре и началам анализа по теме. «Методы решения уравнений и неравенств, содержащих обратные тригонометрические функции». . ...Решение дробных рациональных уравнений
Муниципальное бюджетное общеобразовательное учреждение. «Новомихайловская средняя общеобразовательная школа». Татарского района Новосибирской области. ...Решение двухшаговых уравнений
Тема:. Решение двухшаговых уравнений. . . Цели:. 1) научить находить неизвестное слагаемое в уравнении вида: х+15=68:2;совершенствовать вычислительные ...Решение дробных рациональных уравнений
«. Решение дробно-рациональных уравнений». . Урок: алгебра 9 класс. Тема. :. . Решение дробных рациональных уравнений. Цель:. . познакомить ...Решение биквадратных уравнений
МУНИЦИПАЛЬНОЕ ОБРАЗОВАНИЕ ТАЗОВСКИЙ РАЙОН. Муниципальное казенное общеобразовательное учреждение. Тазовская школа – интернат среднего (полного) ...Методы решение показательных уравнений
Автор: Дементьева Ирина Николаевна. Место работы: МБОУ СОШ №2. с.Кривополянье Чаплыгинского района. Липецкой области. . Должность: учитель ...Решение алгебраических уравнений
Тема: Решение алгебраических уравнений. Цели урока:. . систематизировать, обобщить, расширить знания и умения учащихся, связанные с применением ...Логарифмы и решение логарифмических уравнений
Ибрагимов Рустем Фаткулкадирович. учитель математики. МБОУ «Русско-татарская общеобразовательная средняя школа №81». Урок алгебры и начала ...Методическая разработка Урок математики в 6 классе Решение уравнений (урок закрепления)
Муниципальное образовательное учреждение. Средняя общеобразовательная школа №40 п.г.т. Шерловая Гора. Методическая разработка. Урок математики ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:15 июня 2019
Категория:Математика
Содержит:15 слайд(ов)
Поделись с друзьями:
Скачать презентацию














![Проверка домашнего задания. №1110(в,г) При b=0 |b |-2= |0 |-2 =0-2=-2; При d= 2 -1 |d |+1= | 2-1 |+1= 2-1+1= 2 №1111(в,г) При m=-5/7,n=4 |m+n |:2= |-5/7+4 |:2=23/7:2==23/14. При p=-1,2, q=8 |p-q |:4= |-1,2-8 |:4=9,2:4=2,3. №1132 а)на отрезке [2;6] унаим.=-2,унаиб.= 2; б) на луче [-1;+∞) унаим.= -4,у Проверка домашнего задания. №1110(в,г) При b=0 |b |-2= |0 |-2 =0-2=-2; При d= 2 -1 |d |+1= | 2-1 |+1= 2-1+1= 2 №1111(в,г) При m=-5/7,n=4 |m+n |:2= |-5/7+4 |:2=23/7:2==23/14. При p=-1,2, q=8 |p-q |:4= |-1,2-8 |:4=9,2:4=2,3. №1132 а)на отрезке [2;6] унаим.=-2,унаиб.= 2; б) на луче [-1;+∞) унаим.= -4,у](https://prezentacii.org/upload/cloud/19/06/154537/images/thumbs/screen2.jpg)