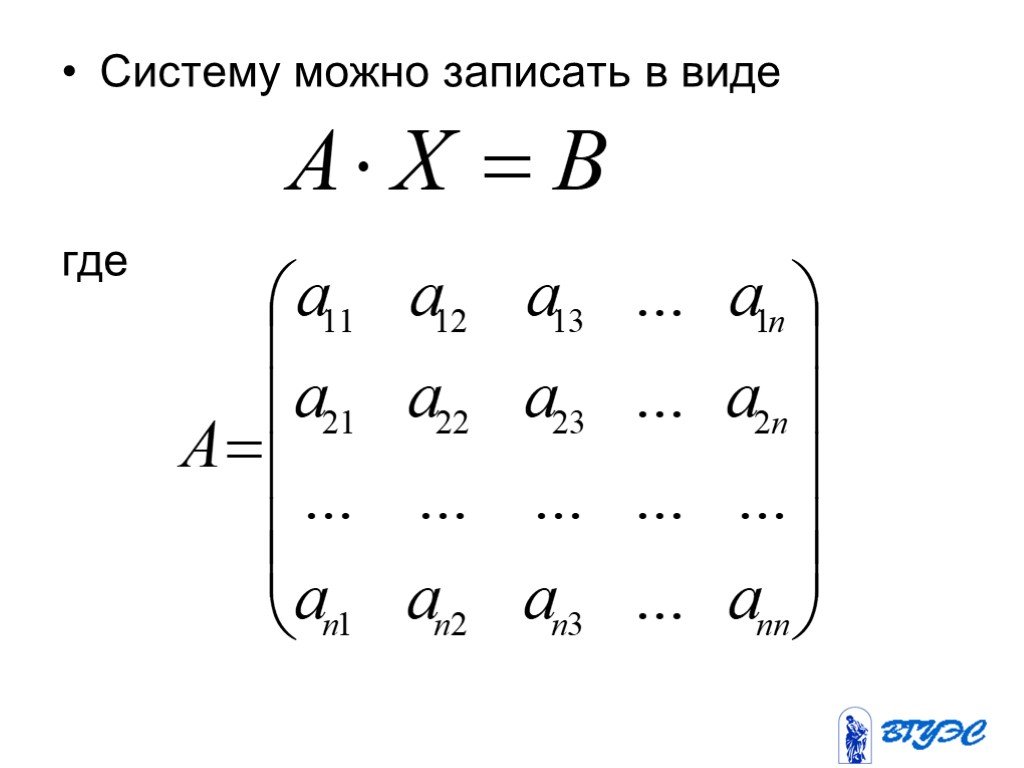
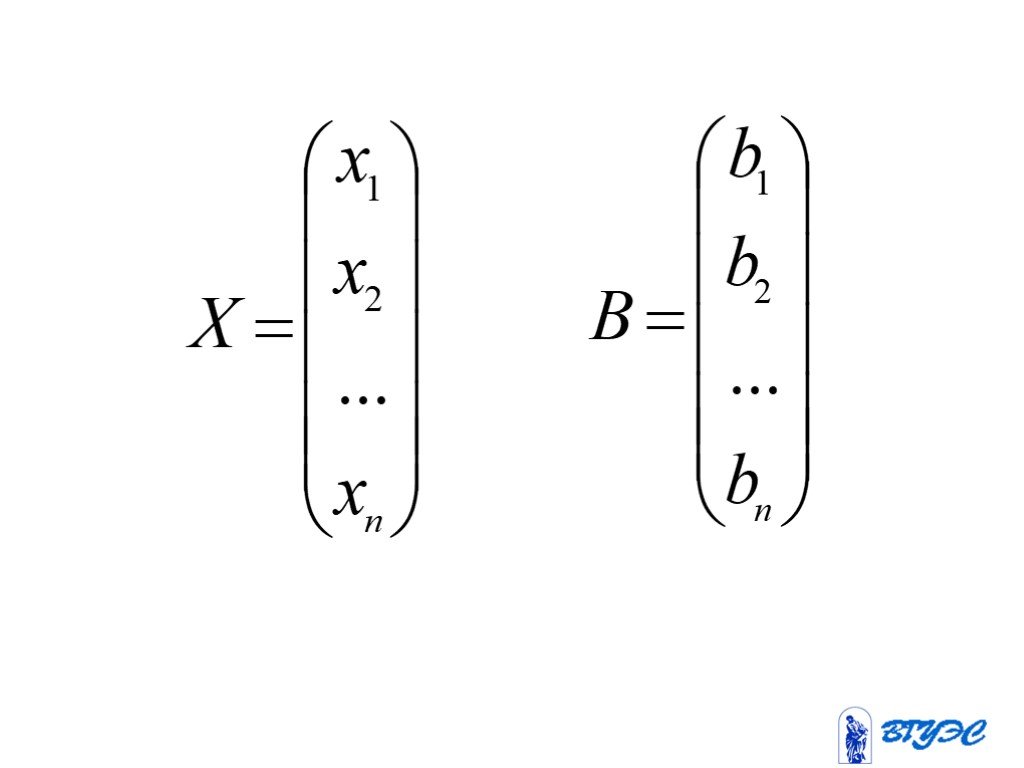
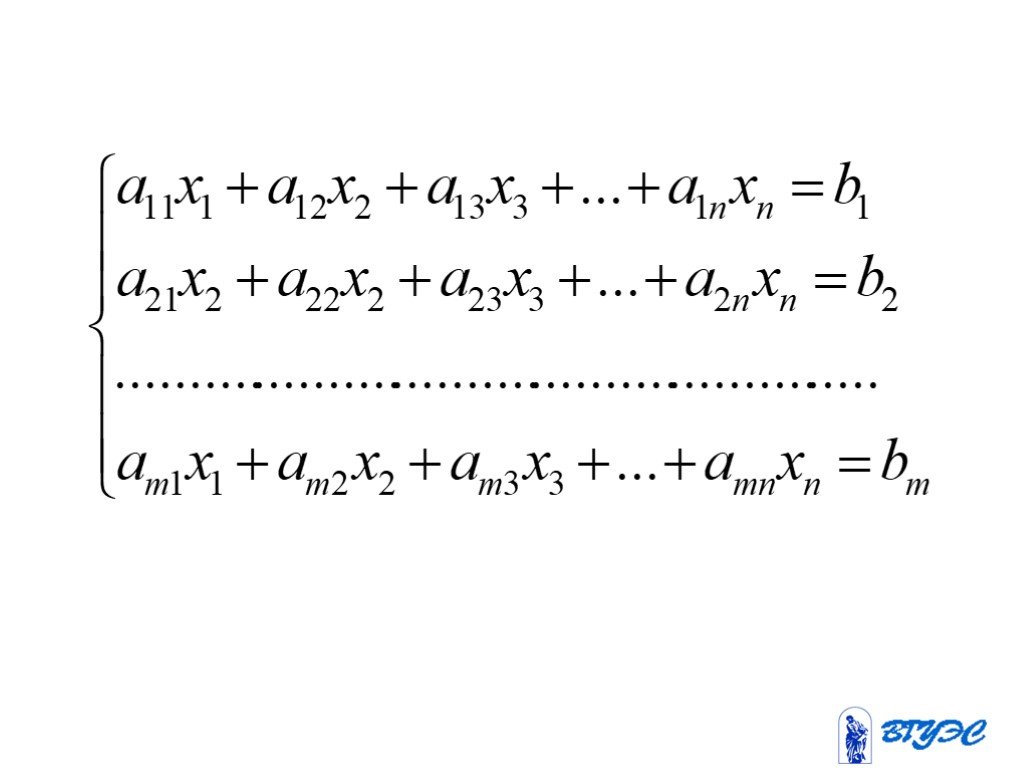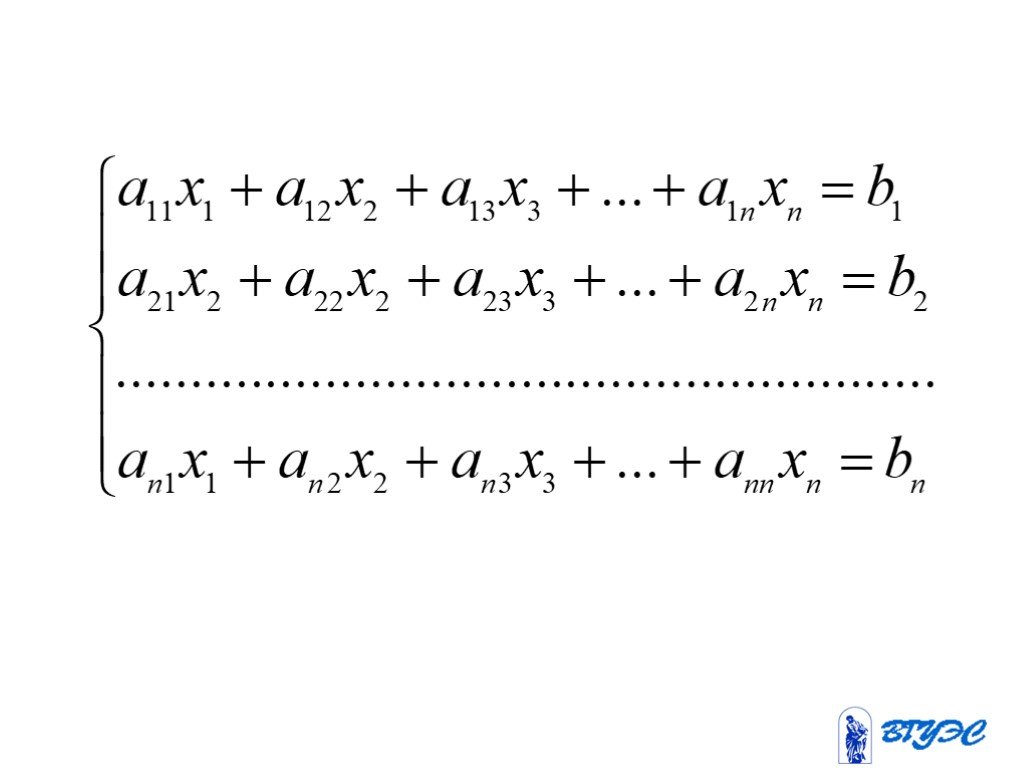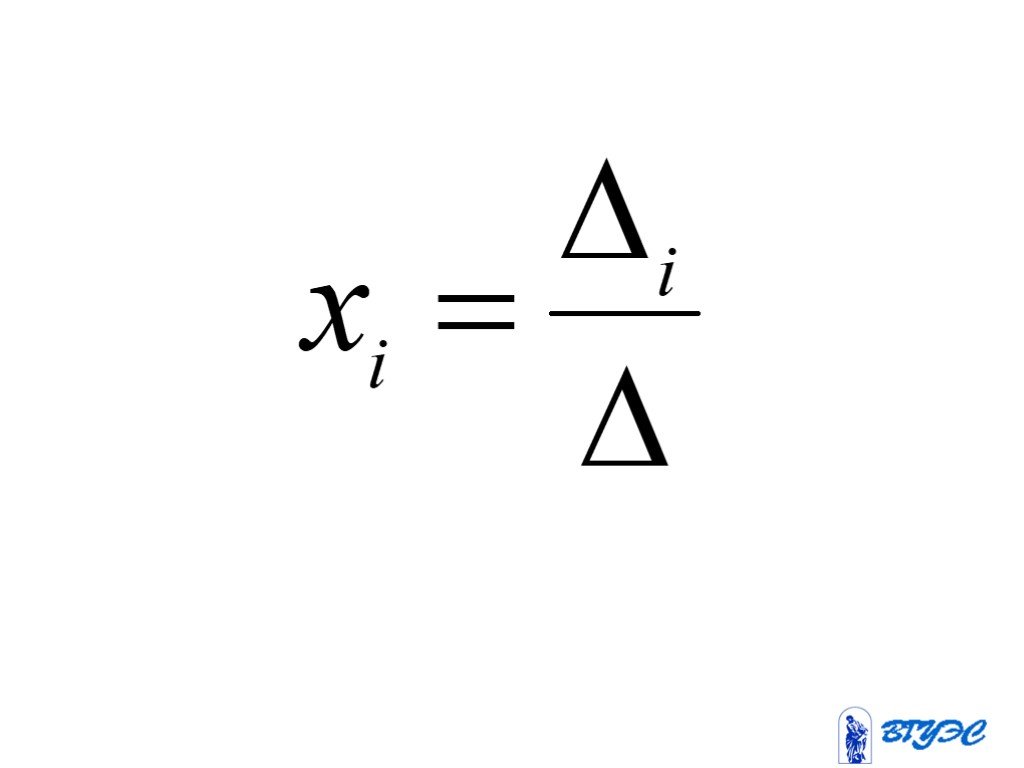Презентация "Системы линейных алгебраических уравнений (СЛАУ)" – проект, доклад
Презентацию на тему "Системы линейных алгебраических уравнений (СЛАУ)" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 35 слайд(ов).
Слайды презентации
Список похожих презентаций
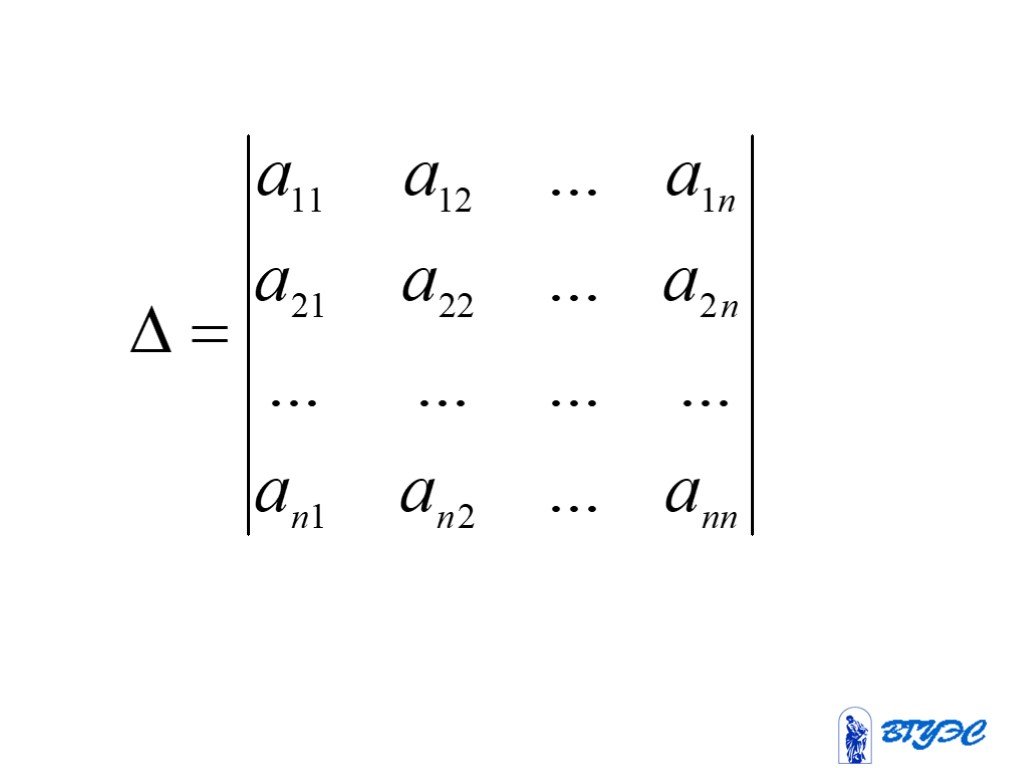
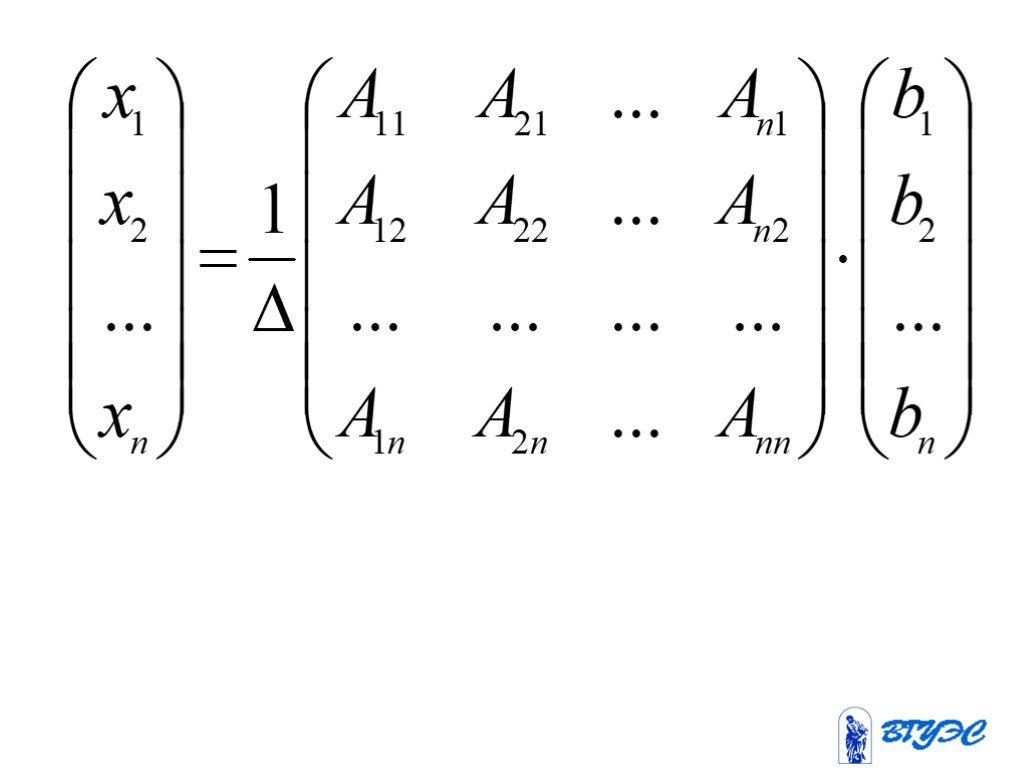
Решение систем линейных алгебраических уравнений с помощью определителей
Цель:. изучить свойства определителей и применить их в решении систем линейных алгебраических уравнений. Задачи исследования:. рассмотрение схем вычисления ...Решение системы линейных уравнений методом Крамера
Системы линейных уравнений. Уравнение называется линейным, если оно содержит переменные только в первой степени и не содержит произведений переменных. ...Автоматизация труда учителя на примере решения систем алгебраических уравнений с использованием программного пакета MATHCAD
Ознакомить учителей математики с возможностями продукта MathCAD Обеспечить автоматизацию работы учителей с использованием MathCAD Рассмотреть решение ...Решение систем линейных уравнений для учителя
Общеобразовательное учебное заведение ПМГ математики. Россия, Тольятти 445057, Приморский б-р, 25 Тел. (8482) 34-51-41 Факс (8482) 4074-56. Алгебра ...Решение задач с помощью линейных уравнений
1 ряд 2 ряд 3 ряд УСТНАЯ РАБОТА ПРОВЕРЬТЕ! -13 1 19 40 7 4 -5 5 -10 -4 -16 Т 6 14 -36 3 О Л И А Э П К НЕН Р Е Н Г С М Ф. (7х + 1) – (6х + 3)= 5 7х ...Решение систем линейных уравнений с двумя неизвестными
1. Запишите систему уравнений 5 х – 3 у + 7, х + 2 у = 15. Напишите уравнение, которое получится, если сложить почленно уравнения данной системы. ...Решение систем линейных уравнений
1.Что называют системой двух линейных уравнений с двумя переменными? 2.Знак системы? 3.Что называют решением системы двух уравнений с двумя переменными? ...Параллельные методы решения систем линейных уравнений
Н.Новгород, 2005 г. Основы параллельных вычислений: Матричное умножение © Гергель В.П. 2 из 44. Постановка задачи Метод Гаусса Последовательный алгоритм ...Решение систем линейных уравнений
Решение систем линейных уравнений. (урок обобщения). Устная работа. Выразите неизвестное у через х: 2х + у=11; 3х – у=9; 7х=9у; х-у=5; 2х – 2у=6; ...Решение линейных уравнений с параметром
Если хочешь строить мост, Наблюдать движенье звезд, Управлять машиной в поле Иль вести машину ввысь, Хорошо работай в школе. Добросовестно учись. ...Решение линейных уравнений, содержащих неизвестное под знаком модуля
ЦЕЛЬ РАБОТЫ. Рассмотреть примеры уравнений, содержащих неизвестное под знаком модуля с точки зрения геометрического смысла модуля и алгебраического ...Решение линейных уравнений, с параметрами, содержащими знак модуля
Решить уравнение |х|=а При рассмотрении вариантов для параметра а необходимо помнить, что модуль принимает только неотрицательные значения. при а0 ...Решение линейных уравнений с одной переменной
Решение линейных уравнений с одной переменной. Определение. Линейным уравнением с одной переменной называется уравнение вида aх + b = с, где а, в, ...Методы решения систем линейных уравнений с двумя переменными
Инженер-электрик: "Это уравнения напряжения или токов в электрической цепи с активными сопротивлениями." Инженер-строитель: "Это уравнения, связывающие ...Решение линейных уравнений с параметрами
Пусть дано уравнение 2х+3=х+а. Здесь х и а – переменные (неизвестные) величины. Переменная а при решении уравнения считается постоянной (т.е. это ...Решение систем двух линейных уравнений с двумя переменными различными способами
Цель урока:. Продолжить формирование навыков сознательного выбора способа решения системы Развивать потребность в нахождении рациональных способов ...Методы решения систем линейных уравнений 1- ой степени
Проверка домашнего задания. Устная работа. Какие способы решения систем линейных уравнений мы знаем? Сколько их? Какой из способов самый наглядный? ...Графический способ решения линейных систем уравнений
Линейная функция – это функция вида y=kx+b , в котором k и b - действительные числа. Графиком линейной функции y=kx+b является прямая. Алгоритм ...Решение нелинейных уравнений
Выбор подходящего метода для решения уравнений зависит от характера рассматриваемой задачи. Задачи, сводящиеся к решению алгебраических и трансцендентных ...Метод Гаусса решения систем линейных уравнений
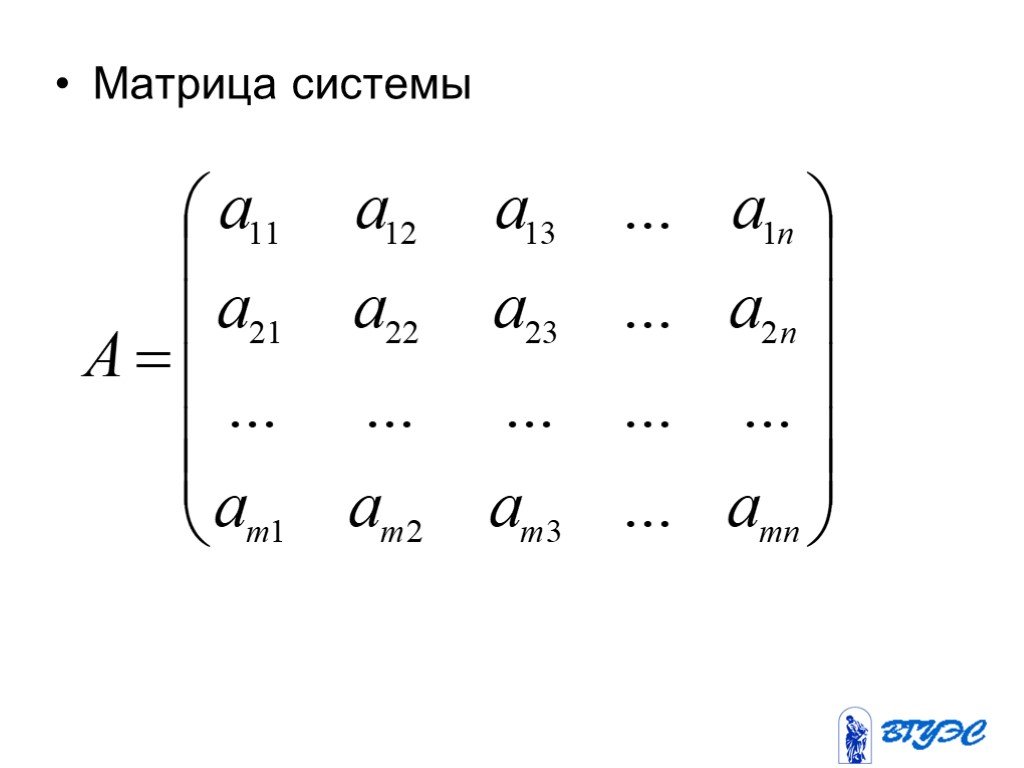
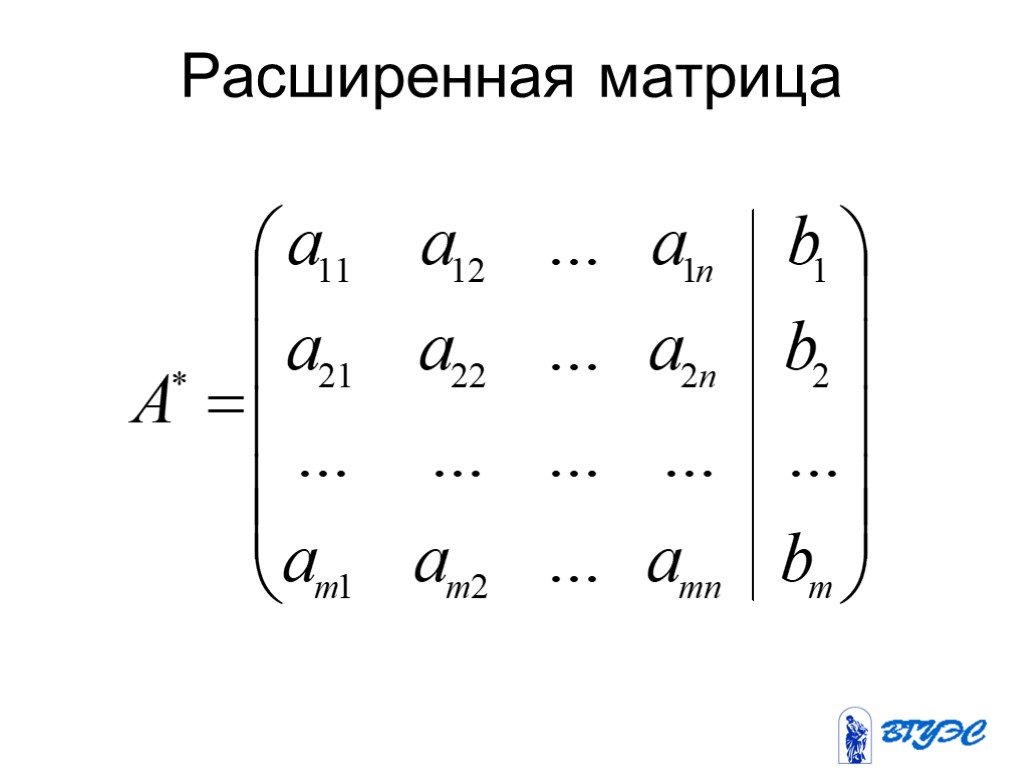
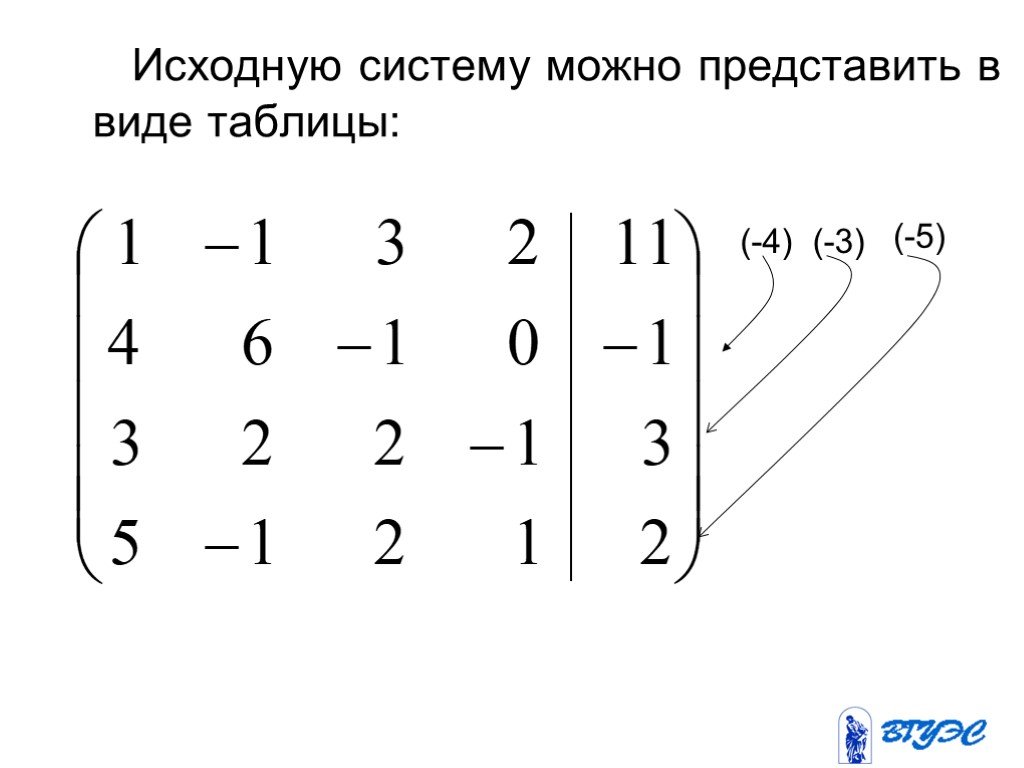
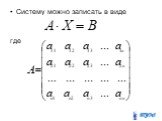
Рассмотрим систему m линейных уравнений с n неизвестными:. Назовем матрицей системы матрицу, составленную из коэффициентов при неизвестных. Матрицу, ...Конспекты
Решение линейных уравнений с одной переменной
Тема: Решение линейных уравнений с одной переменной. Цель: закрепить навыки решения линейных уравнений с одной переменной. Задачи:. Образовательные:. ...Решение задач с помощью линейных уравнений
Мелентьева Ольга Юрьевна. Шг№22 г. Астана. учитель математики. Тема: Решение задач с помощью линейных уравнений. Тип урока:. объяснение новой ...Решение линейных уравнений
Тема:. Решение линейных уравнений. Урок комплексного применения знаний в 6 классе. Цель урока:. . а). Обучающая – . научить решать задачи, ...Решение линейных уравнений
План-конспект урока по математике "Решение линейных уравнений" 6 класс. Урок с использованием цифровых образовательных ресурсов. . Тема: Решение ...Решение линейных уравнений
Тема урока:. . Решение линейных уравнений. Цель:. Повторить решение линейных уравнений; уравнения с модулем; работу с системой координат. ...Решение линейных уравнений
«. №9 орта мектеп» ММ. ГУ «Средняя школа №9». . Открытый урок по математике в 6 классе по теме:. «Решение линейных уравнений». на городском ...Решение задач с помощью систем линейных уравнений
Разработка урока. «Решение задач с помощью систем линейных уравнений». 6 класс. Учитель математики Тансизбаева Г.Н. Задачи урока:. а) ...Решение алгебраических уравнений
Тема: Решение алгебраических уравнений. Цели урока:. . систематизировать, обобщить, расширить знания и умения учащихся, связанные с применением ...Методы решения систем двух линейных уравнений с двумя переменными
План- конспект урока алгебры в 7 классе по теме: «Методы решения систем двух линейных уравнений с двумя переменными». Орг. момент, сообщение ...Решение задач с помощью систем линейных уравнений с двумя переменными
Тема. : Решение задач с помощью систем линейных. . уравнений с двумя переменными. Цель. : создать условия для развития учебно-логических умений ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:1 мая 2019
Категория:Математика
Содержит:35 слайд(ов)
Поделись с друзьями:
Скачать презентацию