Презентация "Прямая. Отрезок" (7 класс) по математике – проект, доклад
Презентацию на тему "Прямая. Отрезок" (7 класс) можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 33 слайд(ов).
Слайды презентации
Список похожих презентаций
Отрезок. Луч. Прямая
1) ВС - отрезок; 2) AN - луч; 3) DE - прямая; 4) ABCD - ломаная; 5) MN - прямая;. 6) С К + KD = CD; 7) АВ - прямая; 8) АВ + ВС + CD – длина ломаной; ...Прямая. Луч. Отрезок
Результаты. Предметные Личностные Метапредметные. Знать:. различие между числами и величинами определения: луча отрезка равных отрезков что через ...Математика «Линии: кривая, прямая. Луч - Отрезок - Точка»
К задуманному числу прибавили 1 и получили 5. Какое число задумали? Какое число при счёте следует за числом 6? Число на 1 меньше, чем 8. Какое число ...Прямая и отрезок
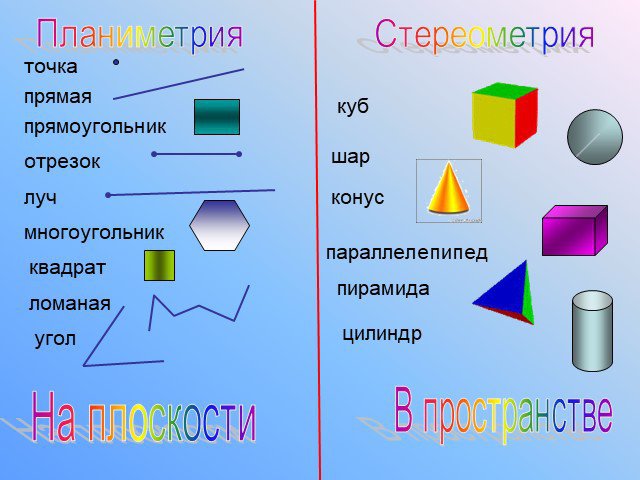
Какие геометрические фигуры вам известны? Геометрия- это наука, занимающая изучением геометрических фигур. ( часть геометрии, в которой рассматриваются ...Начальные понятия планиметрии. Прямая и отрезок. Луч и угол
Вводная беседа.Геометрия в переводе с греческого «землемерие» («гео»- по-гречески земля, а «метрео» - мерить).
Первым, кто начал получать геометрические ...
Прямая и отрезок
Цели урока :. Познакомить учащихся с тем , что изучает геометрия, какой раздел геометрии называется планиметрией, какие фигуры в планиметрии называют ...Прямая и отрезок
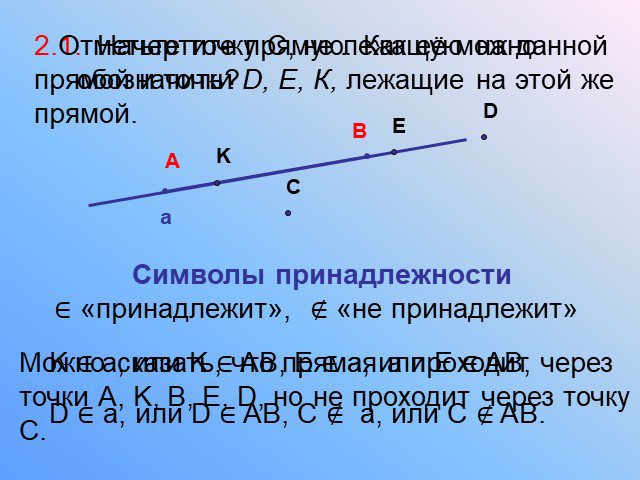
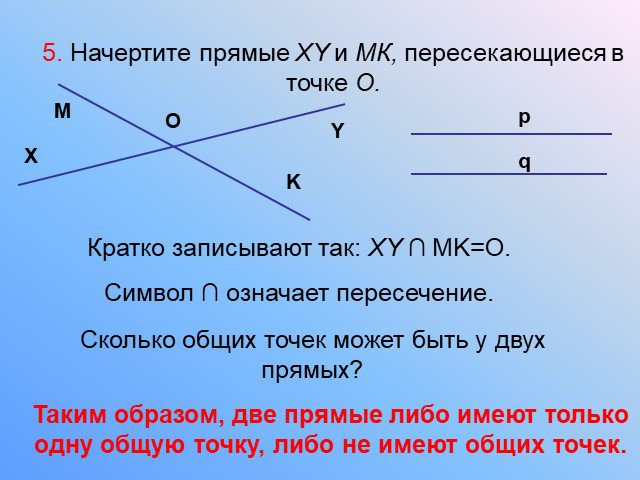
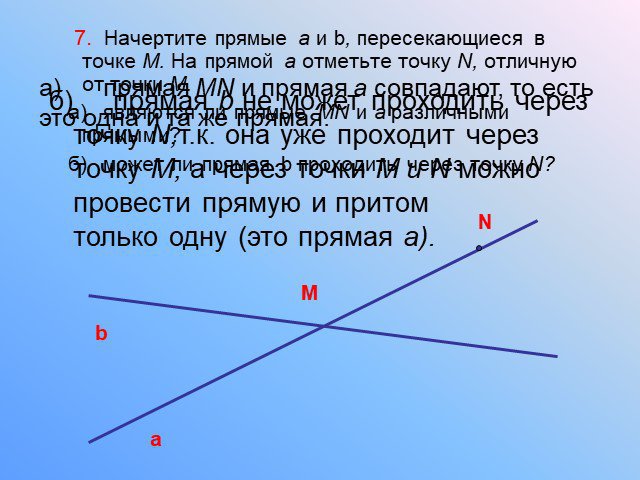
Аксиома 1. Какова бы ни была прямая, существуют точки, принадлежащие ей и точки, не принадлежащие ей. В D F. Аксиома 2. Сколько прямых можно провести ...Прямая и отрезок. Луч и угол. Сравнение и измерение отрезков и углов
1.На прямой отмечены точки А,В,С,Д,Е. а)Какие из данных точек принадлежат отрезку АД, но не принадлежат отрезку СЕ? б)Отметьте точку К так, чтобы ...Прямая в пространстве
Общее уравнение прямой. Прямая линия в пространстве определяется как линия пересечения двух плоскостей. Канонические уравнения прямой. Уравнение прямой, ...Прямая пропорциональность и её график
Мыслю, следовательно существую. Рене Декарт (31,03,1596-11,02,1650) больше известен как великий философ, чем математик. Но именно он был пионером ...Прямая пропорциональность
План урока. Разминка Математический диктант Знакомство с прямой пропорциональностью Решение задач Исследовательская работа Подведение итогов. 1 этап ...Прямая пропорциональная зависимость
Устный счёт: 1. Найдите: 0,3 от 14 0,5 от 300 1,2 от 4 4,3 от 2 2. Составьте верные пропорции из чисел 10, 14, 15, 21. ЗАДАЧА 1 Сколько нужно сахара, ...Прямая на плоскости
Цели и задачи. Цели: Рассмотреть основные понятия по теме «Прямая на плоскости» Задачи: Рассмотреть различные способы задания прямой на плоскости ...Прямая и двойственная задачи и их решение симплекс-методом
Решение симплекс-методом экономической задачи. Решение. Составим ЦФ и ограничения. Найти максимум функции. Запишем задачу в форме основной задачи ...Прямая и обратная пропорциональнось. Решение задач
План урока. Повторение и систематизация теоретических знаний. Повторение и систематизация практических умений. Самостоятельная работа Подведение итогов. ...Прямая и обратная пропорциональность Линейная функция
Прямая y = − x Биссектриса II и VI координатных углов. Прямая пропорциональность y = kx Графиком является прямая, проходящая через начало координат ...Прямая и обратная пропорциональность
ЦЕЛЬ:. Научить узнавать, какой тип пропорциональности содержит данная задача Использовать метод решения задач с помощью пропорции. ХОД УРОКА. 1. Проверка ...Прямая и обратная пропорциональности
а Р=4а. Чтобы вычислить Р надо знать величину а. Говорят: «Р зависит от а » Между величинами а и Р имеется зависимость. У этой зависимости есть одно ...Прямая и обратная пропорциональная зависимости
Выбор ответа с соответствующей буквой загаданного слова: 17-в; 7-л; 0,1-и; 14-с; 0,2-а; 25-к. Найдите пропущенные числа и узнай слово. -101 :3 +37 ...Прямая и луч
Противоположно направленные лучи. Точка пересечения на этом же листе. Точка пересечения за пределами этого листа. . Лучи у которых нет точки пересечения. ...Конспекты
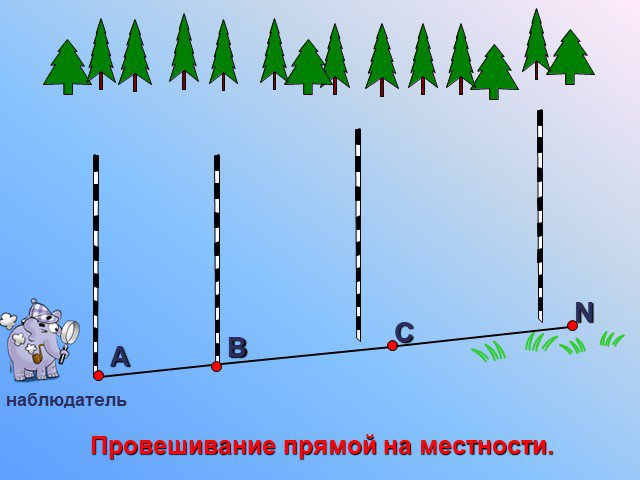
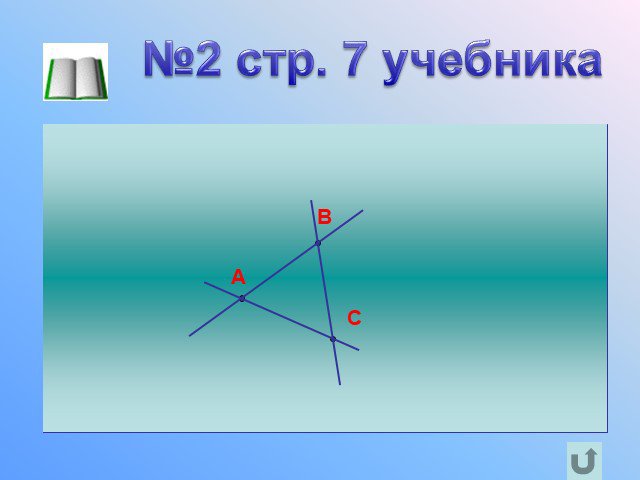
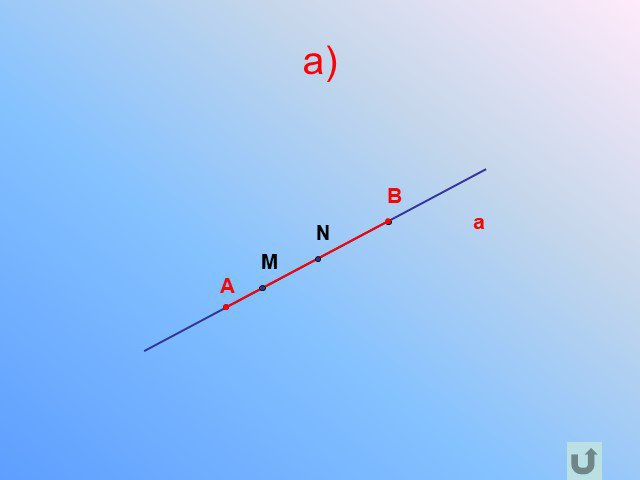
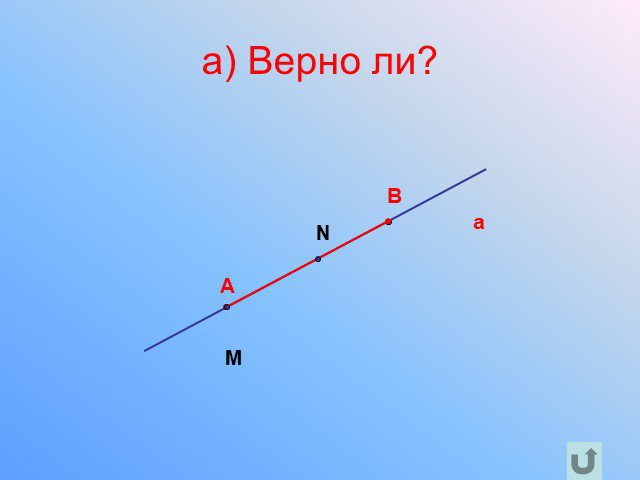
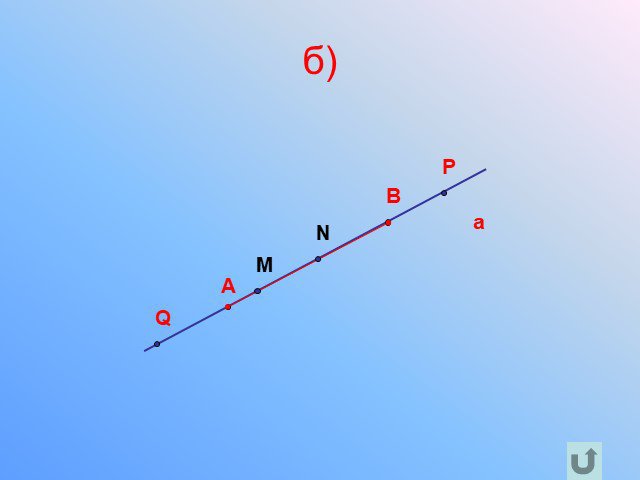
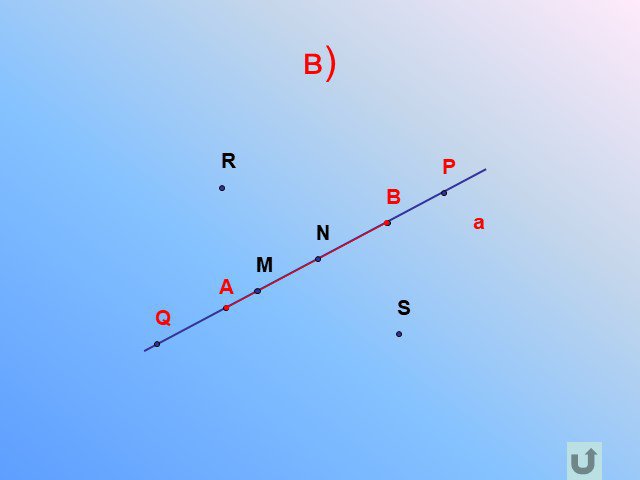
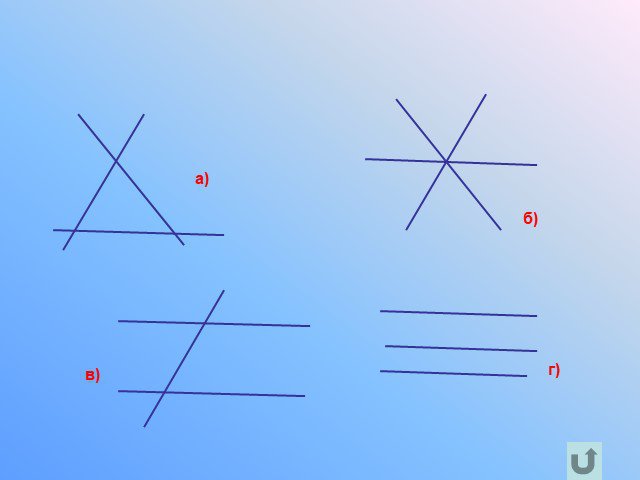
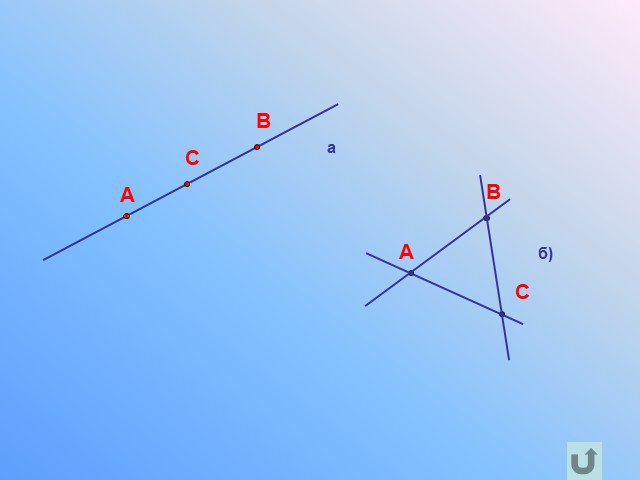
Прямая. Отрезок
Предмет. : геометрия. Класс: 7. . Тема: «Прямая. Отрезок». Тип урока: урок ознакомления с новым материалом. Цели урока:. дидактическая:. ...Прямая и отрезок
Подготовила учитель математики. . МОУ СОШ №93 Набадникова А.Ю. Тема:. Прямая и отрезок. Вид урока: изучение нового материала. Тип урока: комбинированный ...Точка. Прямая линия. Кривая линия. Отрезок
Демина Е.В. . . учитель начальных классов. . МОУ Красноармейская СОШ. Самарская обл. Математика. 1 класс. Тема урока:. «Точка. Прямая ...Прямая и отрезок
Глава: Начальные геометрические сведения. Тема: Прямая и отрезок. Класс: 7. Дата:5.09.2012. № урока в теме: 1урок. Цели урока:. -систематизировать ...Точка. Кривая линия. Отрезок. Прямая линия. Состав числа 5
Григорьева надежда Анатольевна. МКОУ СОШ №12 г.Мирный Архангельской области. Учитель начальных классов. Урок математики. Тема: «Точка. Кривая ...Точка. Кривая линия. Прямая линия. Отрезок. Луч
Тема: Точка. Кривая линия. Прямая линия. Отрезок. Луч. . . Цель:. . Познакомить детей с понятиями: точка, прямая линия, кривая линия, отрезок, ...Луч. Отрезок. Прямая
Урок–путешествие по математике "Луч. Отрезок. Прямая". . Цель. :. . Закрепить понятия: «прямая», «отрезок» и их свойства;. . Познакомить ...Основное свойство пропорции. Прямая и обратная пропорциональная зависимость
Тема:. . Основное свойство пропорции. Прямая и обратная пропорциональная зависимость. . . Цели:. 1.Образовательные:. Повторение действий ...Прямая пропорциональность и ее график
План-конспект урока. Тема урока: «Прямая пропорциональность и её график». ФИО:. Махова Марина Евгеньевна. . Место работы:. МОУ Аббакумовская ...Прямая пропорциональность и ее график
Тема урока: «Прямая пропорциональность и ее график». Обучающие и развивающие цели:. обеспечить усвоение темы на уровне:. Знания. – ученик должен ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:21 марта 2017
Категория:Математика
Классы:
Содержит:33 слайд(ов)
Поделись с друзьями:
Скачать презентацию