Презентация "Дифференциальное исчисление функции одной переменной" по математике – проект, доклад

Дифференциальное исчисление функции одной переменной.

Определение производной

Производной функции y=f(x) в точке х0 Называется , если этот предел существует. Производная обозначается или . Таким образом, =.

Таблица производных

Правила Дифференцирования

Пусть u=u(x) и v=v(x) – функции, дифференцируемые в точке х. Тогда в этой точке дифференцируемы функции u+v, u∙v, . Последнее при условии, что v´(x)≠0. Причем, (u+v)´=u´+v´, (uv)´=u´v+uv´, .

Производная сложной функции

Пусть y=f(u), а u=φ(x). Тогда функция y=f(φ(x)) называется сложной функцией от х. Теорема. Если функция u=φ(x) имеет производную в точке х, а функция y=f(u) имеет производную в соответствующей точке u=φ(x), то сложная функция y=f(φ(x)) имеет производную в точке х, причем .

Дифференцирование функций, заданных параметрически

Пусть функция y от х задана параметрически уравнениями: x=x(t), y=y(t), t (α;β).

Пример

x=cos3t, y=sin3t. Вычислить yx´´.

поэтому

Дифференцирование функций, заданных неявно.

Вычислить y´x, если y5+xy-x2=0. Продифференцируем обе части по х. Получим 5y4y´+y+xy´-2x=0, откуда y´(5y4+x)=2x-y и

Логарифмическое дифференцирование

Найти производную функции y=(sinx)x. Логарифмируем функцию по основанию е: lny=x.lnsinx. Дифференцируем обе части равенства по х: ∙y´=lnsinx+x∙ctgx отсюда y´=y∙(lnsinx+x∙ctgx) или y´=(sinx)x∙(lnsinx+x∙ctgx).

Дифференциал функции

dy=f´(x)∙dx

Некоторые теоремы о дифференцируемых функциях!

Теорема Ферма

Пусть функция y=f(x) определена в интервале (a;b) и принимает в точке с этого интервала наибольшее или наименьшее на (a;b) значение. Если существует f´(c), то f´(c)=0

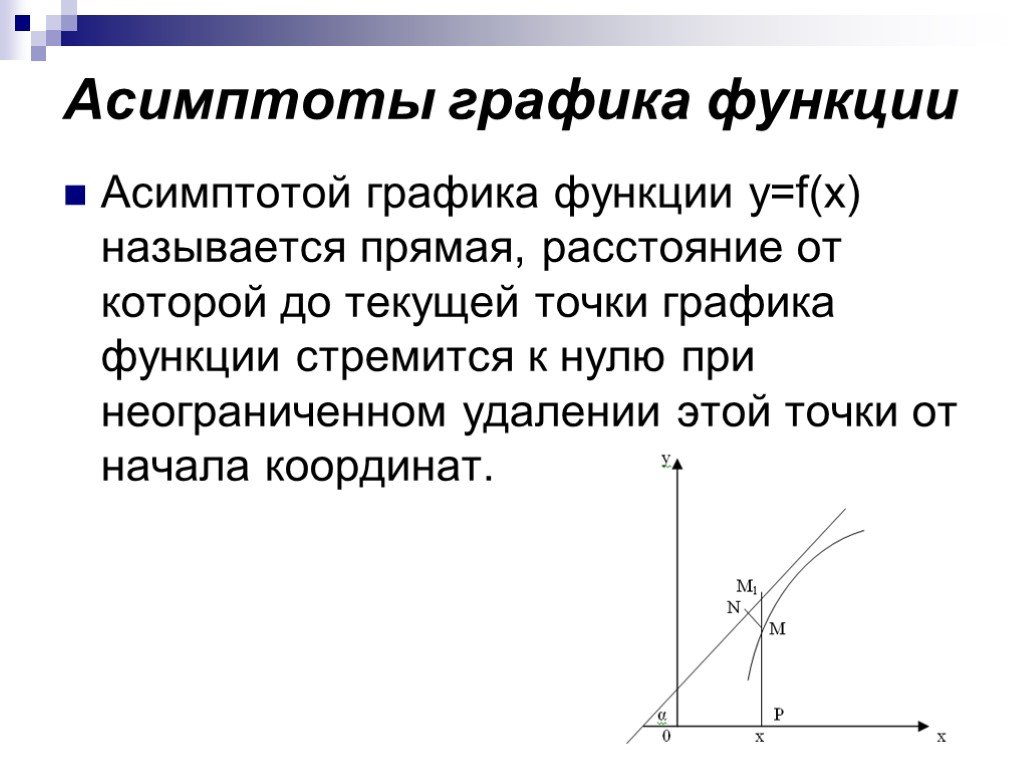
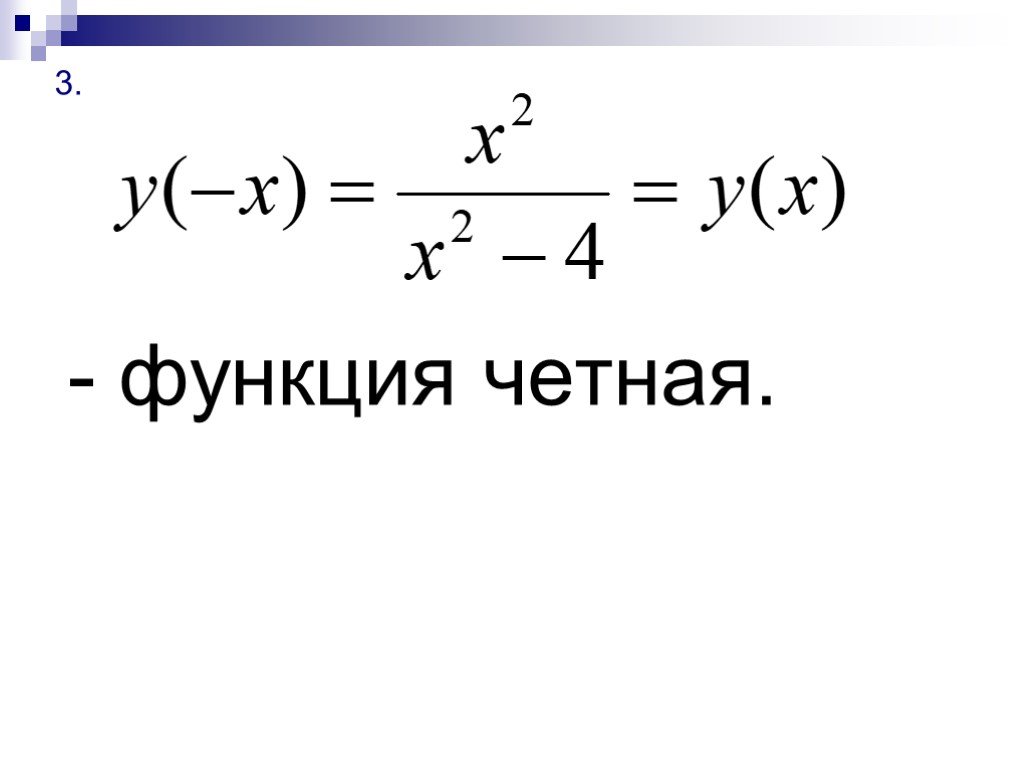
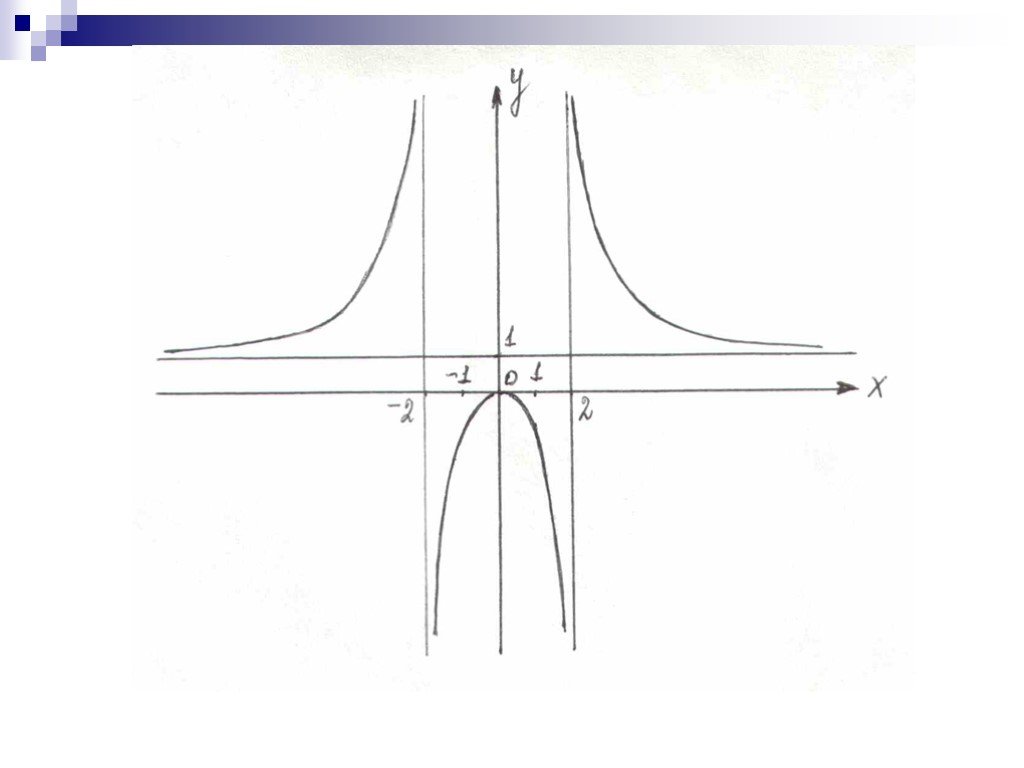
Теорема Ролля

Пусть функция y=f(x) непрерывна на отрезке [a;b], дифференцируема на интервале (a;b) и f(a)=f(b)=0. Тогда ее производная f´(х) обращается в ноль хотя бы в одной точке c (a;b).

Теорема Лагранжа

Пусть функция y=f(x) непрерывна на отрезке [a;b] и дифференцируема в интервале (a;b). Тогда существует хотя бы одна точка c (a;b), для которой выполняется условие:

Теорема Лопиталя (правило Лопиталя).

Пусть f(x) и φ(x) – функции, непрерывные на [a;b], дифференцируемые на (a;b); φ´(x)≠0 при всех х (a;b) и f(a)=φ(a)=0. Тогда если существует , то существует причем :

Применение производной к исследованию функций

Экстремумы функции.

Необходимо условие монотонности функции

Если дифференцируемая в интервале (a;b) функция y=f(x) возрастает (убывает) на (a;b), то для всех х(a;b) f´(x)≥0 (f´(x)≤0)

Достаточный признак существования экстремума

Если непрерывная на интервале функция y=f(x) имеет производную f´(x) во всех точках этого интервала, за исключением, может быть, критической точки с, принадлежащей этому интервалу, и если f´(x) при переходе аргумента слева направо через критическую точку с меняет знак с плюса на минус (с минуса на плюс), то функция в точке с имеет максимум (минимум)

Выпуклость и вогнутость графика функции

График дифференцируемой функции называется выпуклым (вогнутым) в интервале (a;b), если он расположен ниже (выше) любой своей касательной на этом интервале

Достаточный признак выпуклости и вогнутости

Пусть функция y=f(x) имеет вторую производную f´(x) во всех точках интервала (a;b). Если во всех точках этого интервала f´(x)0), то график на (a;b) выпуклый (вогнутый).

Достаточный признак существования точки перегиба

Если вторая производная f´(x) непрерывной функции меняет знак при переходе аргумента через точку х0, то точка (x0;f(x0)) является точкой перегиба графика функции.

Асимптоты графика функции

Асимптотой графика функции y=f(x) называется прямая, расстояние от которой до текущей точки графика функции стремится к нулю при неограниченном удалении этой точки от начала координат.

План исследования функции и построение графика

Область определения функции. Точки пересечения графика функции с осями координат. Четность, нечетность функции. Исследование функции на непрерывность. Вертикальные асимптоты. Невертикальные асимптоты. Интервалы монотонности и экстремумы. Интервалы выпуклости, вогнутости и точки перегиба. Дополнительные точки, , периодичность (по мере необходимости). Построение графика.

Пример Исследовать функцию и построить ее график.

Область определения: так как при х=-2 и х=2 знаменатель дроби обращается в ноль.

(-∞;-2) (-2;2) (2;+∞),

2. Пусть х=0, тогда у=0. Пусть у=0, тогда , откуда х=0. (0;0) – точка пересечения графика с осями координат

- функция четная.

4. Функция имеет разрывы в точках х=-2 и х=2, так как f(-2) и f(2) не определены. , , , , следовательно, х=-2 и х=2 – точки разрыва II рода и прямые х=-2 и х=2 – вертикальные асимптоты.

5.Невертикальные асимптоты следовательно, прямая у=1 – асимптота.

6. у´=0, если -8х=0, откуда х=0 – критическая точка. Откуда х=-2 и х=2 – критические точки. На интервалах (-∞;-2) и (-2;0) функция возрастает, а на интервалах (0;2) и (2;+∞) – убывает. Уmax(0)=0.

7. у´´≠0 при х(-∞;∞), х=-2 и х=2 – критические точки второго порядка. На интервалах (-∞;-2) и (2;+∞) – график функции вогнутый, а на интервале (-2;2) – выпуклый. Точек перегиба нет