Конспект урока «Формулы сокращенного умножения. Квадрат суммы и квадрат разности двух выражений» по алгебре для 7 класса
Негосударственное образовательное учреждение
«Средняя общеобразовательная школа с углубленным изучением
отдельных предметов имени В.Д.Чурсина »
г. Ставрополь
Конспект урока алгебры
в 7 классе
. «Формулы сокращенного умножения.
Квадрат суммы и квадрат разности двух выражений.»
автор учитель математики
Лаврушова Юлиана Евгеньевна
Тема урока. Формулы сокращенного умножения. Квадрат суммы и квадрат разности двух выражений.
Тип урока. Закрепление знаний.
Цель урока. Выработать навыки использования формул квадрата суммы и квадрата разности двух выражений.
Задачи.
-
Обобщить и систематизировать теоретические знания.
-
Развивать познавательные процессы, память, мышление, внимание, наблюдательность, сообразительность.
-
Реализовать метапредметный подход на основе развития мыследеятельности, воображения учащихся.
-
Воспитать интерес к истории математики.
Ход урока.
1. Актуализация. (Ориентировочно - мотивационный этап)
Учитель. Здравствуйте ребята. Вы начали изучать тему «Формулы сокращенного умножения», а в течение последних уроков занимались по теме «Квадрат суммы и квадрат разности двух выражений». Сегодня мы систематизируем и закрепим знания по теме «Формулы сокращенного умножения. Квадрат суммы и квадрат разности двух выражений».
-
Организация работы. (Информационно – поисковый этап).
Учитель. Ребята, а что такое формула?
Ученики. 1) точное определение понятия или закона. 2) математический закон, выраженный алгебраическими знаками.
Учитель. А я вам предлагаю узнать, как показала роль формулы С.Ковалевская. Правильный ответ отметьте в тетради на печатной основе (Приложение 1.
| а6 | а5 | а3 | |
| | У | в | к |
| 8 | 8 | 64 | 16 |
| | химии | математики | физики |
| 6х8 | 6х8 | Збх8 | З6х4 |
| бывает | существует | живет | |
| 4в9 | 16в18 | 4в18 | 16в9 |
| | свой | твой | мое |
| 0,2у5 | 0,2у10 | 0,4у5 | 0,04у1° |
| | жест | движение | язык |
| с2в3 | с4в6 | с2в6 | с4в3 |
| | это | то | другое |
| З хбу7 | 9хбу7 | 9х12у14 1 | Зх12у14 |
| | задачи | формулы | выражения |
«У математики существует свой язык — это формулы». С.Ковалевская (Слайд 3)
Учитель. Обращаю ваше внимание, что формула это краткая запись правил, закономерностей.
3. Генерализация (Обобщение)
Учитель. Ребята, а кто может записать формулы «Квадрат суммы и квадрат разности двух выражений».
Двое учащихся записывают формулы квадрата суммы и квадрата разности на доске.
(а + в)2 = а2 + 2ав + в 2
(а - в)2 = а 2 - 2ав + в 2
Учитель. Сформулируйте правило.
Учащиеся. Квадрат суммы ( разности ) равен квадрату первого выражения плюс( минус) удвоенное произведение первого и второго плюс квадрат второго выражения .
Учитель. Ребята, мы одно и тоже правило представили по — разному, какими видами формулирования правил мы пользовались?
Учащиеся. Словесным.
Учитель . (показать на формулы) А это какой способ ?
Учащиеся. Символьный.
Учитель. Эти правила были известны около 4 тысяч лет назад, Их сформулировал известный математик
4 Контроль знаний. (Слайд 4) Выполнив следующее задание, вы узнаете его имя. Учащиеся выполняют номер у доски . ( 2х + 3 )2 (6 — 7а )2 (* + 5х)2 = у2 + 10ху + 25х 2 (За - *)2 = 9а 2 - 12ав + 4в2 р 2 - 2pq + q 2 64 + 16в + в 2
Проверка (Слайд 5)
Учитель. Это великий математик древности Евклид. Евклид занимался измерением площадей. Он является основоположником геометрии. Свой способ он описал в трактате «Начала». (Слайд 6) Как можно назвать этот способ?
Учащиеся. Евклид использовал геометрический способ.
Учитель. Сделайте вывод. Какие способы задания правила существует?
Учащиеся. Символьный. Словесный. Геометрический.
Учитель. Какой наиболее рациональный?
Учащиеся. Символьный.
Учитель. Почему?
Учащиеся. Он наиболее краткий, удобный.
Учитель. Предлагаю следующее задание. Посмотрите на примеры. Как используя формулы можно решить эти примеры? (Слайд 7)
Учащиеся. Можно представить в виде суммы или разности двух выражений.
612 = ( 60 + 1 )2 = 3600 + 120 + 1 = 3721
792 = ( 80 - 1 )2 = 6400 - 160 + 1= 6241
Учитель. Воспользуйтесь справочным материалом и вы узнаете какой латинской буквой стали обозначать вторую степень. (Приложение 3)
Учащиеся. Q
5. Эвристический этап урока (Открытие)
Учитель. Посмотрите на слайд (Слайд 8). Перед вами план школьной спортивной площадки. Она имеет квадратную форму. Необходимо застелить площадку современным покрытием. Скажите, как можно посчитать площадь поля?
Учащиеся. Площадь отдельно каждой ячейки, или площадь всей площадки.
Учитель. Правильно. Предлагаю рассчитать площадь покрытия для каждой части.(если необходимо разное цветовое решение)
Учащиеся заполняют таблицу. Проверка (Слайд 9)
| а | в | с | |
| а | а2 | ав | ас |
| в | ав | в2 | св |
| с | ас | св | с2 |
Учитель. Ребята, давайте запишем сумму площадей всех частей. (Слайд 10)
(а+в+с)2= а2+в2+с2+2ав+2вс+2ас
Учитель. Как можно назвать данное равенство?
Учащиеся. Формула квадрата суммы трех выражений.
6. Самостоятельная работа. (Слайд 11) Приложение 2.
Проверьте себя (Слайд 12).
7. Рефлексия
Учитель. Какими формулами мы пользовались на уроке? Сколько способов представления правил вы узнали? Перечислите.
Спасибо за урок.
Использованные материалы и Интернет-ресурсы
-
Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова; под ред. С. А. Теляковского – М.: Просвещение, 2011.
-
Алгебра. Дидактические материалы. 7 класс/ В. И. Жохов, Ю. Н. Макарычкв, Н. Г. Миндюк. – М.: Просвещение, 2010.
-
Алгебра. 7 класс. Учебник. Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б. 18-е изд., стер. - М.: 2009. - 240 с. 2009.
-
Геометрия. 7-9 классы. Учебник. Атанасян Л.С. и др. 20-е изд. - М.: Просвещение, 2010.
-
http://ru.wikipedia.org/wiki/%C4%E8%EE%F4%E0%ED%F2_%C0%EB%E5%EA%F1%E0%ED%E4%F0%E8%E9%F1%EA%E8%E9
-
http://ru.wikipedia.org/wiki/%CA%EE%E2%E0%EB%E5%E2%F1%EA%E0%FF,_%D1%EE%F4%FC%FF_%C2%E0%F1%E8%EB%FC%E5%E2%ED%E0
-
http://ru.wikipedia.org/wiki/%C5%E2%EA%EB%E8%E4
-
http://ru.wikipedia.org/wiki/%C2%EE%E7%E2%E5%E4%E5%ED%E8%E5_%E2_%F1%F2%E5%EF%E5%ED%FC
-
http://ru.wikipedia.org/wiki/%C4%E5%EA%E0%F0%F2,_%D0%E5%ED%E5
Приложение 1
ФИ
Тема урока .Формулы сокращенного умножения. Квадрат суммы и квадрат разности двух выражений.
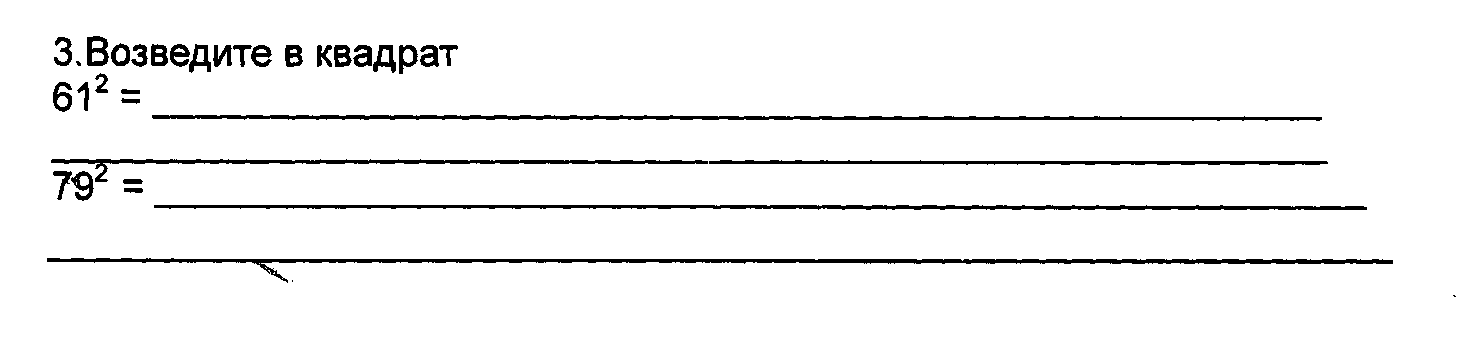
1.Возведите в квадрат
| а6 | а5 | а3 | |
| | У | в | к |
| 8 | 8 | 64 | 16 |
| | химии | математики | физики |
| 6х8 | 6х8 | Збх8 | З6х4 |
| бывает | существует | живет | |
| 4в9 | 16в18 | 4в18 | 16в9 |
| | свой | твой | мое |
| 0,2у5 | 0,2у10 | 0,4у5 | 0,04у1° |
| | жест | движение | язык |
| с2в3 | с4в6 | с2в6 | с4в3 |
| | это | то | другое |
| З хбу7 | 9хбу7 | 9х12у14 1 | Зх12у14 |
| | задачи | формулы | выражения |
2.Выполнив следующее задание , вы узнаете имя великого математика.
| | |
| (6 — 7а )2 | |
| (* + 5х)2 = у2 + 10ху + 25х 2 | |
| (За - *)2 = 9а 2 - 12ав + 4в2 | |
| р 2 - 2pq + q 2 | |
| 64 + 16в + в 2 | |
4. Запишите отдельно площадь каждой ячейки. Заполните таблицу.
| а | в | с | |
| а | | | |
| в | | | |
| с | | | |
Приложение 2
Самостоятельная работа
1.
| | |
| ( 2к — 0,4 ) 2 | |
| ( * + 6х )2 = в 2 + 12хв + * х 2 | |
| (7а - *)2 = 49а 2 - * а + с2 | |
| к 2 — 8кq + 16q 2 | |
| 25 + 10в + в 2 | |
2. Найдите ошибку ( 2 - 7а )2 = 4 + 28а + 49а 2 (к + 4с )2 = к2 + 4кс + 16с2 х2 — 10ху + 25у 2 = ( х - 5у ) 2 1 + 0,6в + 0,09в 2 = (0,3в + 1 )2
3. Решите уравнение ( 2 - а )2= а2+ 56
Приложение 3
Историческая справка
Со́фья Васи́льевна Ковале́вская (урождённая Корвин-Круковская; 3 [15] января 1850, Москва — 29 января [10 февраля] 1891, Стокгольм) — русский математик и механик, с 1889 года иностранный член-корреспондент Петербургской Академии наук. Первая в России и в Северной Европе женщина-профессор и первая в мире женщина-профессор математики.
Евкли́д или Эвкли́д (др.-греч. Εὐκλείδης, от «добрая слава», ок. 300 г. до н. э.) — древнегреческий математик, автор первого из дошедших до нас теоретических трактатов по математике. Его научная деятельность протекала в Александрии в 3 в. до н. э.
Диофа́нт Александри́йский (др.-греч. Διόφαντος ὁ Ἀλεξανδρεύς; лат. Diophantus) — древнегреческий математик, живший предположительно в III веке н. э.
Первая книга Диофанта предварена обширным введением, в котором описаны используемые Диофантом обозначения. Неизвестную Диофант называет «числом» (ἀριθμός) и обозначает буквой ς, квадрат неизвестной — символом 
(сокращение от δύναμις — «степень»). Предусмотрены специальные знаки для следующих степеней неизвестного, вплоть до шестой, называемой кубо-кубом, и для противоположных им степеней. Знака сложения у Диофанта нет: он просто пишет рядом положительные члены, причём в каждом члене сначала записывается степень неизвестного, а затем численный коэффициент.
В 3 веке Диофант записывал квадратную степень термином dunamis - греч. сила.
В 7 веке вторая степень имела вид – ВА (в записи Брахмагупты)
Брахмагупта (санскр. ब्रह्मगुप्त, ок. 598—670) — индийский математик и астроном. Руководил обсерваторией в Удджайне. Оказал существенное влияние на развитие астрономии в Византии и странах ислама.
Рене́ Дека́рт (фр. René Descartes лат. Renatus Cartesius — Картезий; 31 марта 1596, Лаэ (провинция Турень), ныне Декарт (департамент Эндр и Луара) — 11 февраля 1650, Стокгольм) — французский философ, математик, механик, физик и физиолог, создатель аналитической геометрии и современной алгебраической символики.
В 16 веке существовало более десяти обозначений для квадрата. Например CE(от census лат. - сила). Наиболее распространенное обозначение – Q. Исторически степень, начиная с Декарта, обозначали «двухэтажной» записью вида 
. Когда появились компьютеры и компьютерные программы, возникла проблема, состоящая в том, что в тексте компьютерных программ невозможно записать степень таким способом. В связи с этим изобрели особые значки для операции возведения в степень.
Первым таким значком были две звёздочки: **, используемые в языке Фортран. В появившемся несколько позже языке Алгол использовался значок стрелки: 
(о такой стрелке см. Стрелки Кну́та). Язык BASIC предложил символ ^ («циркумфлекс»), который приобрёл наибольшую популярность. Его теперь часто используют и при написании формул и математических выражений в текстовых файлах.
Примеры: 3^2=9; 5^2=25; 2^3=8; 5^3=125
На компьютерной клавиатуре значок степени (циркумфлекс) находится на той же клавише, что и цифра 6. Для его ввода надо в режиме набора английского текста нажать Shift+6.
Здесь представлен конспект к уроку на тему «Формулы сокращенного умножения. Квадрат суммы и квадрат разности двух выражений», который Вы можете бесплатно скачать на нашем сайте. Предмет конспекта: Алгебра (7 класс). Также здесь Вы можете найти дополнительные учебные материалы и презентации по данной теме, используя которые, Вы сможете еще больше заинтересовать аудиторию и преподнести еще больше полезной информации.
Список похожих конспектов
Формулы сокращённого умножения. Квадрат суммы и разности двух выражений
Муниципальное бюджетное общеобразовательное учреждение. гимназия № 19 им.Н.З.Поповичевой г.Липецка. Урок по алгебре в ...
Формулы сокращённого умножения. Квадрат суммы и разности двух выражений
Муниципальное бюджетное общеобразовательное учреждение. гимназия № 19 им.Н.З.Поповичевой г.Липецка. Конспект урока по ...
Формулы квадрата суммы и квадрата разности двух выражений
Коммунальное государственное учреждение. . Тюменская основная школа. Формулы квадрата суммы и квадрата разности. двух выражений. Алгебра-7 ...
Формулы сокращенного умножения. Разность квадратов двух выражений
МОУ «Горская средняя общеобразовательная школа». . Красненского района Белгородской области. Интегрированный урок алгебры. по теме:. «Формулы ...
Возведение в квадрат суммы и разности двух выражений
Голубцова Ирина Николаевна. МБОУ «СОШ № 4» с. Сотниковское. Учитель математики. Урок по алгебре. 7 класс. Тема:. «Возведение в квадрат ...
Квадрат суммы, квадрат разности, умножение разности двух выражений на их сумму
Иванова Марина Викторовна. МАОУ СОШ № 54 г. Томск. Учитель математики. Обобщающий урок по теме. «Квадрат суммы, квадрат разности, умножение ...
Возведение в квадрат суммы и разности двух выражений
Кудрявцева О.А., учитель математики МБОУ «Средняя общеобразовательная школа №15» г. Калуги. . Возведение в квадрат суммы и разности двух выражений. ...
Возведение в квадрат и в куб суммы и разности двух выражений
Конспект урока алгебры по теме:. «Возведение в квадрат и в куб суммы и разности двух выражений». 7класс. Учитель математики. Гнутова ...
Возведение в квадрат суммы и разности двух выражений
МКОУ «Гавриловская средняя общеобразовательная школа». Учитель математики Панкратова Нина Владимировна. ПЛАН-КОНСПЕКТ УРОКА ПО АЛГЕБРЕ 7 КЛАСС. ...
Формулы куба суммы и куба разности двух выражений
Тема:. . Формулы куба суммы и куба разности двух выражений. . Цели урока:. . : 1. Отработка навыков применения формул «куб суммы и разности двух ...
Квадрат суммы. Квадрат разности
Тема урока: "Квадрат суммы и квадрат разности". 7-й класс. . Нуждина Алёна Владимировна, учитель математики. . . Цели урока:. . Формирование ...
Квадрат суммы и квадрат разности
План-конспект урока. . ФИО (полностью). . Облакова Ирина Анатольевна. . . . Место работы. . Муниципальное бюджетное общеобразовательное ...
Разложение на множители с помощью квадрата суммы и квадрата разности
МАОУ Видновская гимназия. учитель математики. высшей квалификационной категории. педагогический стаж 17 лет. Кондратьева Татьяна Юрьевна. ...
Формулы сокращенного умножения
Урок математики в 7 классе. Подготовила учитель математики Умирбаева К.У. Тема урока. Формулы сокращенного умножения. Цель:. . 1. Образовательная: ...
Формулы сокращенного умножения
Обобщающий урок по главе «Формулы сокращенного умножения». Предмет:. алгебра. Класс:. 7А. Тип урока:. урок-практикум. Цели и задачи урока:. ...
Формулы сокращенного умножения
МБОУ «Матюшинская СОШ». Верхнеуслонского района Республики Татарстан. Урок математики в 7классе. Тема урока « Формулы сокращенного ...
Формулы сокращенного умножения
8. . План - конспект открытого урока. по технологии развивающего обучения. . на тему:. . «Формулы сокращённого умножения». ...
Формулы сокращенного умножения
МБОУ гимназия №2 г. Гурьевска. Калининградской области. Конспект урока алгебры в 7-м классе. "Квадрат суммы. Квадрат разности. Разность ...
Преобразование выражений, содержащих операцию извлечения квадратного корня
Урок-обобщение. «Преобразование выражений, содержащих операцию извлечения квадратного корня». 8 класс. Цели урока:. Обобщить знания по всем ...