Конспект урока «Сумма бесконечно убывающей геометрической прогрессии» по алгебре для 9 класса
Дата: 24.12.2012 Алгебра 9 рус
Тема урока: Сумма бесконечно убывающей геометрической прогрессии
Цели и задачи урока: Научить приёмам комбинирования формул, определений, свойств арифметической и геометрической прогрессий. Научить приёму оформления задач через таблицу.
Развить навыки применения формул, составления уравнений, систем уравнений и методов их решений. Развить математический кругозор, мышление, математическую речь;
Воспитать активную работу на уроке, сознательное отношение к учёбе, интерес к изучению математики, воспитывать стремление к непрерывному совершенствованию.
План урока.
-
Организационный момент.
-
Немного истории.
-
Теоретический опрос.
-
Решение задач.
-
Рефлексия. Ответьте на вопросы сами себе.
-
Домашнее задание.
Ход урока.
-
Организационный момент.
-
Немного истории.
В клинописных табличках вавилонян, в египетских папирусах, относящихся ко 2 тысячелетию до нашей эры, встречаются примеры арифметических и геометрических прогрессий. Первые теоретические сведения, связанные с прогрессиями, дошли до нас в документах Древней Греции. Некоторые формулы, относящиеся к прогрессиям, были известны и индийским учёным. Правило для нахождения суммы членов произвольной арифметической прогрессии даётся в «Книге абака» (1202г.) Леонардо Фибоначчи. А общее правило для суммирования любой конечной геометрической прогрессии встречается в книге Н. Шюке «Наука о числах», в 1484 году.
-
Теоретический опрос.
Задание. Записать номер формулы.
-
Определение арифметической прогрессии.
-
Формулу суммы n-первых членов арифметической прогрессии через первый член и последний.
-
Формулу суммы членов бесконечно убывающей геометрической прогрессии.
-
Формулу суммы n-первых членов геометрической прогрессии.
-
Общую формулу для вычисления разности арифметической прогрессии.
-
Формулу свойства членов геометрической прогрессии.
-
Формулу суммы n-первых членов арифм-кой прогрессии через первый член и разность.
-
Общую формулу для вычисления знаменателя геометрической прогрессии.
-
Определение геометрической прогрессии.
-
Формулу n-го члена геометрическую прогрессии.
-
Формулу свойства членов арифметической прогрессии.
-
Формулу n-го члена арифметической прогрессии.
-
an+1 = an + d 7)
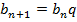
-
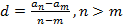 8)
8) 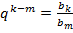
-
an = a1 + (n – 1)d 9)
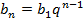
-
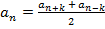 0)
0) 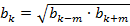
6) ![]() 11)
11) ![]()
![]() 12)
12) ![]()
Проверить код ответов ( 1, 6, 12, 11, 2,0.
Расшифровать полученные числа, как день16.12.11. 20-летия Независимости Казахстана.
-
Решение комбинированных задач.
-
Даны 4 числа. Первые 3 из них составляют геометрическую
прогрессию со знаменателем 2, а последние 3 - арифметическую прогрессию с
разностью 6. Найти данные числа.
Дано: а, в, с, е – искомые числа. Из них геометр. прогрессия{ а, в, с} и q = 2,
арифмет.прогрессия{ в, с, е} и d = 6.
Найти: а, в, с, е.
Решение:
| а | в | с | е | |
| Геометр. прогрессия | а | аq = 2а | аq2 = 4а | - |
| Арифмет. прогрессия | - | в | в + d = в + 6 | в + 2d = в + 12 |
По таблице видно, что 2а = в и 4а = в + 6.
Имеем 4а = 2а + 6, 2а = 6, а = 3. Тогда в = 2![]()
Ответ: 3, 6, 12, 18.
-
Сумма трёх чисел, образующих арифмет. прогрессию, равна 27.
Если от этих чисел отнять соответственно 1; 3; 2, то полученные числа будут
образовывать геометрическую прогрессию. Найти исходные три числа.
Дано: а, в, с – искомые числа, арифмет. прогрессия { а, в, с},
геометр. прогрессия {а – 1, в – 3, с – 1}.
Найти: а, в, с.
| а | в | с | |
| Арифмет. прогрессия | а | в = а + d | с = а + 2d |
| Геометр. прогрессия | а - 1 | (а + d) – 3 | а + 2d – 2 |
По данным составим таблицу.
-
По условию сумма трёх чисел, образующих арифметическую прогрессию, равна 27, тогда можно записать: а + а + d + а + 2d = 27, 3а + 3d = 27, а + d = 9 (1).
По данным таблицы получили при решении в = 9, так как в = а + d.
-
Используем свойство членов геометрической прогрессии. Получим уравнение:
(а + d – 3)2 = (а – 1)(а + 2d – 2), (9 – 3)2 = (а – 1)( а + d + d – 2), 62 = (а – 1)(7 + d) (2)
Составим систему уравнений из уравнений (1) и (2) решим её.
![]()
![]() d2 – d – 20 = 0
d2 – d – 20 = 0
По теореме Виета и ей обратной найдём корни полученного уравнения:![]()
Найдём искомые числа: 1) а = 9 – (– 4) = 13, в = 9, с = 9 – 4 = 5.
2) а = 9 – 5 = 4, в = 9, с = 9 + 5 = 14.
Ответ: 13, 9, 4 или 4, 9, 14.
-
Даны 4 числа, составляющих геометрическую прогрессию. Если от
этих чисел отнять соответственно 10; 11; 9; 1, то полученные числа будут
образовывать арифметическую прогрессию. Найти данные числа.
Дано: а, в, с, е – искомые числа. Из них геометр. прогрессия { а, в, с, е},
арифмет. прогрессия { а – 10, в – 11, с – 9, е – 1}.
Найти: а, в, с, е. Решение: По данным составим таблицу.
| а | в | с | е | |
| Геометр. прогрессия | а | аq | аq2 | аq3 |
| Арифмет. прогрессия | а – 10 | в – 11 = аq – 11 | с – 9 = аq2 – 9 | е – 1 = аq3 – 1 |
По таблице используем данные и применим свойство арифметической прогрессии 1) ![]() , 2аq – 22 = a + аq2 – 19, аq2 - 2аq + a = – 3,
, 2аq – 22 = a + аq2 – 19, аq2 - 2аq + a = – 3,
a(q2 - 2q + 1) = – 3, a(q – 1)2 = – 3 (1).
2) ![]() , 2аq2 – 18 = aq + аq3 – 12, аq3 - 2аq2 + aq = – 6,
, 2аq2 – 18 = aq + аq3 – 12, аq3 - 2аq2 + aq = – 6,
aq(q2 - 2q + 1) = – 6, aq(q – 1)2 = – 6 (2).
-
Почленно разделим равенство (2) на равенство (1)
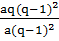 =
= 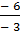 ,
,
После сокращения дробей получим q = 2.
-
Найдём значение а из равенства (1) а = – 3.
Вычислим остальные числа: в = – 3 · 2 = – 6, с = – 6 ·2 = – 12, е = – 12 · 2 = –24.
Ответ: – 3, – 6, – 12, – 24.
-
Даны 3 различных числа, составляющих геометрическую
прогрессию. Необходимо между вторым и третьим членом этой
последовательности вставить число, чтобы получившаяся последовательность
была арифметической прогрессией. Найти знаменатель заданной
геометрической прогрессии.
Дано: а, в, с – искомые числа, геометрическая прогрессия { а, в, с},
арифметическая прогрессия { а, в, х, с}.
Найти: q
Решение: Так как по условию 3 различных числа, составляющих геометрическую прогрессию, то q![]() для арифметической прогрессии d
для арифметической прогрессии d ![]()
| а | в | х | с | |
| Геометр. прогрессия | а | аq | - | аq2 |
| Арифмет. прогрессия | а | а + d | а + 2d | а + 3d |
По таблице видно, что 1) аq = а + d, d = аq – а, d = а(q – 1) (1)
2 ) аq2 = а + 3d, 3d = аq2 – а , 3 d = а(q2 – 1) (2)
-
Подставим равенство (1) в равенство (2) 3а(q – 1) = а(q2 – 1).
Разделим полученное равенство на а(q – 1) ![]() , получим 3 = q + 1, q = 2. Ответ: 2.
, получим 3 = q + 1, q = 2. Ответ: 2.
-
Решить неравенство (3х + 7 + 3 – 1 – …)(2 + 4 + 8 + …+ х)
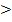 0, где в скобках по 6 числовых слагаемых.
0, где в скобках по 6 числовых слагаемых.
Решение. 1) Рассмотрим числовые слагаемые первой скобки: 7; 3; - 1;…
Заметим, что 3 – 7 = – 4, – 1 – 3 = – 4 раз другие слагаемые не предлагаются, значит эта закономерность сохраняется и эти 6 слагаемых и они образуют арифметическую прогрессию с d = – 4 и а1 = 7.
По формуле суммы n-первых членов арифметической прогрессии найдём сумму 6 членов: ![]()
-
Рассмотрим числовые слагаемые второй скобки: 2; 4; 8;…
Заметим, что 4 : 2 = 8: 4 = 2 раз не другие слагаемые не предлагаются, значит эта закономерность сохраняется и все 6 слагаемых образуют геометрическую прогрессию с
q = 2 и в1 = 2.
По формуле суммы n-первых членов геометрической прогрессии найдём сумму 6 членов: ![]()
-
Полученные данные подставим в заданное неравенство (3х – 18)(126 + х)
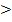 0 и решим его методом интервалов.
0 и решим его методом интервалов.
![]()
П
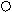
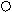

 остроим чертёж + –– +
остроим чертёж + –– +
– 126 6
Ответ: (- ![]()
-
Решить уравнение х2 – 6│х│ – 21 – 15 – 9 - … = 3 + 2 + 1 + 0,5 + ….. где в левой части уравнения 8 числовых слагаемых.
Решение.
-
Рассмотрим числовые слагаемые левой части уравнения: - 21; - 15; - 9;…
Заметим, что – 21 – (– 15) = – 15 – (– 9) = 6, раз другие слагаемые не предлагаются, значит эта закономерность сохраняется и эти 8 слагаемых образуют арифметическую прогрессию с d = 6 и а1 = – 21.
По формуле суммы n-первых членов арифмет. прогрессии найдём сумму 8 членов: ![]()
-
Рассмотрим числовые слагаемые правой части уравнения без числа 3: 2; 1; 0,5;…
Заметим, что 1 : 2 = 0,5: 1 = 0,5 раз не другие слагаемые из этой последовательности не предлагаются, значит эта закономерность сохраняется и все слагаемые образуют бесконечно убывающую геометрическую прогрессию с q = 0,5 и в1 = 2.
По формуле суммы членов бесконечно убывающей геометрической прогрессии найдём сумму всех членов: ![]()
-
Подставим полученные результаты в уравнение х2 – 6│х│+ 0 = 3 + 4 и решим его.
х2 – 6│х│ = 7, х2 – 6│х│ – 7 = 0. Раскроем модуль по определению.
Если х![]() то уравнение примет вид х2 – 6х – 7 = 0. Найдём его корни по второму свойству коэффициентов квадратного уравнения
то уравнение примет вид х2 – 6х – 7 = 0. Найдём его корни по второму свойству коэффициентов квадратного уравнения ![]()
Если х![]() то уравнение примет вид х2 + 6х – 7 = 0. Найдём его корни по первому свойству коэффициентов квадратного уравнения
то уравнение примет вид х2 + 6х – 7 = 0. Найдём его корни по первому свойству коэффициентов квадратного уравнения ![]()
Ответ: ![]()
-
Рефлексия. Ответьте на вопросы сами себе.
-
Домашнее задание.
-
Три числа составляют арифметическую прогрессию с разностью равной 4. Если к третье число увеличить на 8, эти три числа будут образовывать геометрическую прогрессию. Найти данные числа. (2, 6, 10)
-
Даны три числа образующих геометрическую прогрессию, первое из которых равно 8. Если второе число увеличить на 1, то эта последовательность станет арифметической прогрессией. Найти знаменатель геометрической прогрессии.(1,5 или 0,5)
-
Даны четыре числа. Первые три образуют геометрическую прогрессию, а последние три - арифметическую прогрессию. Сумма первого и последнего чисел равна 32, а сумма средних чисел – 24. Найти данные числа.(32, 16, 8, 0 или 2, 6, 18, 30)
Здесь представлен конспект к уроку на тему «Сумма бесконечно убывающей геометрической прогрессии», который Вы можете бесплатно скачать на нашем сайте. Предмет конспекта: Алгебра (9 класс). Также здесь Вы можете найти дополнительные учебные материалы и презентации по данной теме, используя которые, Вы сможете еще больше заинтересовать аудиторию и преподнести еще больше полезной информации.

