Конспект урока «Начнем с показательных уравнений» по алгебре
Начнем с показательных уравнений.
Во-первых, давайте определимся:
1. если мы возводим в положительную степень:
-
целое число, то в результате получим целое число
-
дробное число, то в результате получим дробное число
2. если мы возводим в отрицательную степень:
-
целое число, то в результате получим дробное число
-
дробное число, то в результате получим целое число:
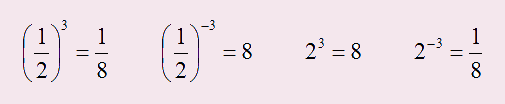
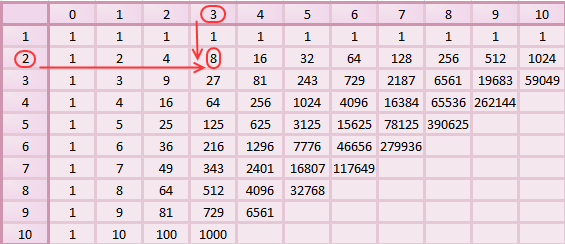
Во-вторых, надо знать таблицу степеней или хотя бы уметь ей пользоваться:
В- третьих, при решении показательных уравнений, Ваша задача добиться того, чтобы основания левой и правой части стали одинаковы:

Рассмотрим пример из единой базы ЕГЭ:
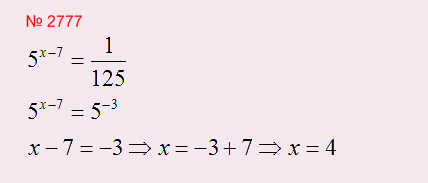
Теперь разберем логарифмические уравнения:
Результат логарифма - это число, представляющее из себя степень в которую возводят основание логарифма и получают логарифмическую часть:

В нашем случае: результат логарифма - это 2, основание - это 5, а логарифмическая часть -это 25.
Принцип решения логарифмических уравнений такой же как и при решении показательных уравнений: необходимо добиться того, чтобы основания логарифмов в левой и правой частях уравнений были одинаковы. в этом случае можно будет приравнять друг к другу логарифмические части:
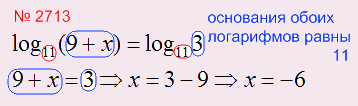
В случае, если в правой части уравнения стоит число, то Ваша задача привести это число к логарифму. Любое число можно представить через логарифм с нужным для Вас основанием:
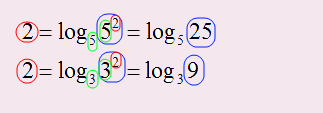
В первом случае, мы число 2 представили через логарифм с основанием 5 (т.к. 5 в квадрате это 25, то логарифмическая часть равна 25), а во втором случае число представили через основание 3, т.к. 3 в квадрате это 9, то логарифмическая часть равна 9.
Бывают ситуации, когда основанием является не число, а переменная:
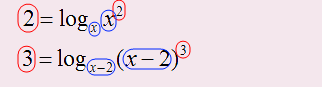
В первом случае число два представляем через логарифм с основанием х, а во втором случае число три через основание (х-2).
Давайте рассмотрим примеры, когда в правой части уравнения стоит число:
1. В основании стоит число:
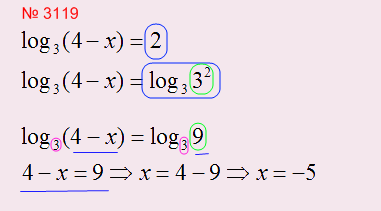
Число 2 представили через логарифм с основанием три. т.к. в левой части стоит логарифм с основанием три, в результате основания логарифмов получились одинаковые, а значит можно приравнять логарифмические части друг к другу, а далее решаем обычное линейное уравнение.
2. В основании стоит переменная:
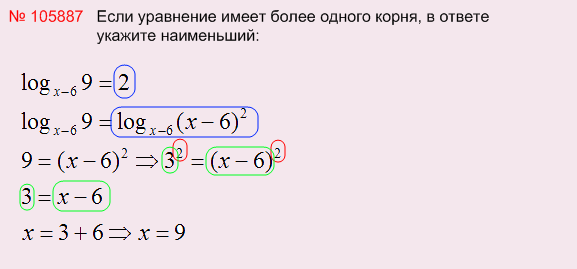
Число 2 представили через логарифм с основанием (х-6), т.к. такое основание у логарифма из левой части уравнения. Основания получились одинаковые, поэтому можно приравнять к друг другу логарифмические части, далее 9 надо представить через какое-либо число в степени 2 (почему 2? - в правой части выражение (х-6) возводится в квадрат, поэтому и в левой части надо возводить в квадрат). Этим числом является три, далее решаем линейное уравнение.
При решении логарифмических уравнений в задании В5 встречаются уравнения, где надо использовать некоторые свойства логарифмов. Я расскажу только о двух, встречающихся в этих уравнениях:
1. Число стоящее перед логарифмом можно внести в степень логарифмической части.
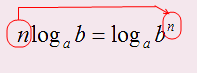 Разберем пример с использованием этого свойства:
Разберем пример с использованием этого свойства:
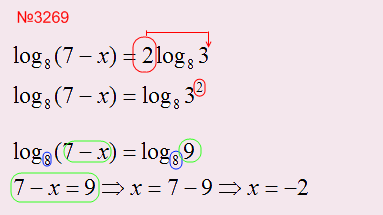
2. Сумму двух логарифмов с одинаковыми основаниями можно преобразовать в один логарифм следующим образом:
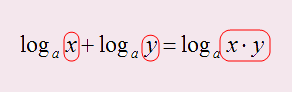 Разберем пример на это свойство:
Разберем пример на это свойство:
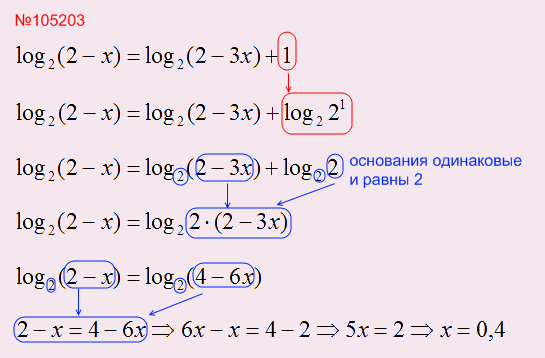
Итак, тригонометрические уравнения задания В5 ЕГЭ по математике, содержат три функции: sinx, cosx и tgx. Во-первых, надо знать значения тригонометрических функций:
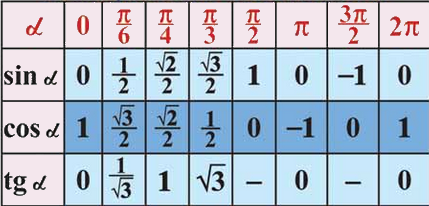
Во-вторых формулы, которые используют при решении тригонометрических уравнений:
1. Функция y=sinx.
Функция ограниченная: находиться в пределах [-1;+1]. Это значит, что при решении уравнений типа sinx=5 или sinx=-2 в ответе получается: нет корней, но в блоке В мы не можем записать такой ответ в бланк, значит уравнения должны давать какой-то конечный ответ.
Формулы для функции y=sinx:
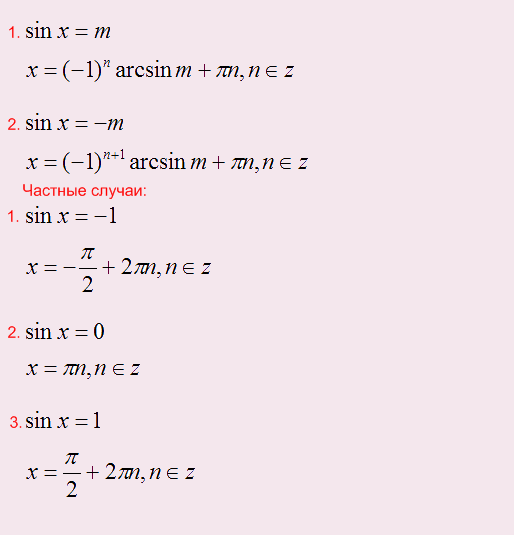
Решим уравнение и в ответе напишем наибольший отрицательный корень:
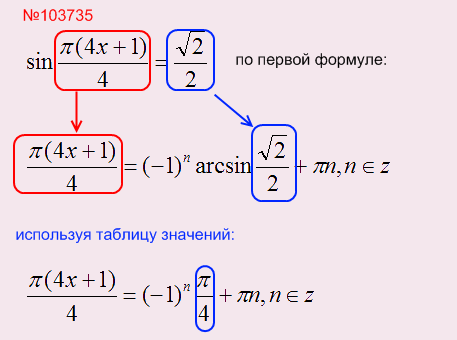

Уравнение мы решили, но в ответ надо записать наибольший отрицательный корень. Для этого в уравнение вместо n надо подставлять следующие целые числа и считать результаты: 0, +1, -1, +2, -2, +3, -3 и т.д. до тех пор пока не найдете нужный Вам ответ:
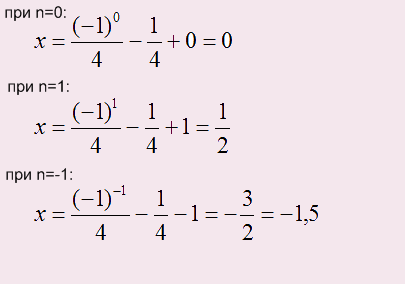
Наибольший отрицательный корень: -1,5.
2. Функция у=cosx.
Функция тоже ограниченная: находиться в пределах [-1;+1]. Это значит, что при решении уравнений типа cosx=2 или cosx=-4 в ответе получается: нет корней, но в блоке В мы не можем записать такой ответ в бланк, значит уравнения должны давать какой-то конечный ответ.
Формулы для функции y=cosx:

Решим уравнение и в ответе напишем наибольший отрицательный корень:

Уравнение мы решили, но в ответ надо записать наибольший отрицательный корень. Для этого в уравнение вместо n надо подставлять следующие целые числа и считать результаты: 0, +1, -1, +2, -2, +3, -3 и т.д. до тех пор пока не найдете нужный Вам ответ:
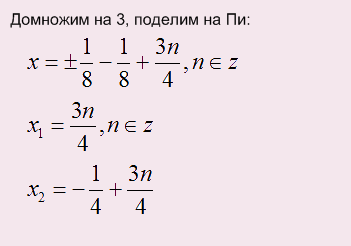
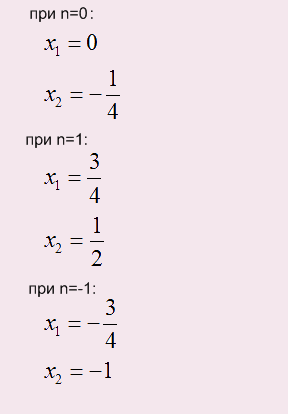
Наибольший отрицательный корень: -0,25
3. Функция y=tgx.
Тут всего одна формула, без частных случаев:
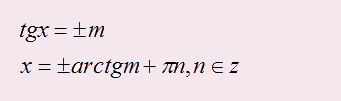
Решим уравнение и найдем наименьший отрицательный корень:

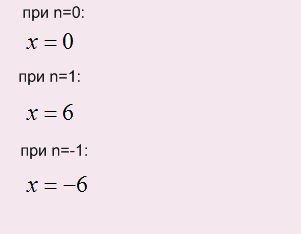
Наименьший положительный корень х=6.
Кроме тригонометрических уравнений встречаются еще ииррациональные уравнения.
Для решения иррациональных уравнений необходимо возвести в квадрат обе части уравнения, чтобы избавиться от корня.
Разберем на примере:
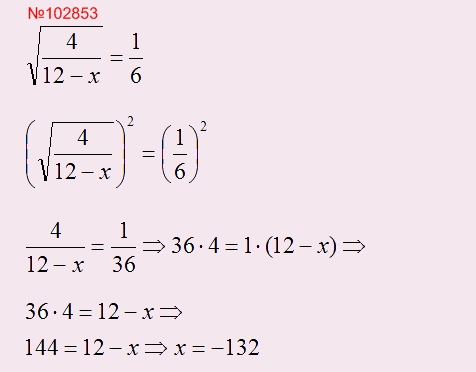
Здесь представлен конспект к уроку на тему «Начнем с показательных уравнений», который Вы можете бесплатно скачать на нашем сайте. Предмет конспекта: Алгебра Также здесь Вы можете найти дополнительные учебные материалы и презентации по данной теме, используя которые, Вы сможете еще больше заинтересовать аудиторию и преподнести еще больше полезной информации.

