Презентация "«Метод математической индукции»" по математике – проект, доклад
Презентацию на тему "«Метод математической индукции»" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 15 слайд(ов).
Слайды презентации
Список похожих презентаций
Элементы математической статистики
Содержание. Введение Генеральная совокупность и выборка Способы отбора Статистическое распределение выборки Эмпирическая функция распределения Статистические ...Элементы математической статистики, комбинаторики и теории вероятностей. Сочетания и размещения. Часть I
Содержание. Введение Пример 1. Учительница подготовила к контрольной работе… Решения: 1.а) 1.б) 1.в) 1.г) Пример 2. Известно, что х = 2аЗb5с и а, ...Усвоение математической терминологии. Табличные случаи умножения и деления
1. 6 • 3. 2. 8 • 7. 3. 49 : 7. 4. 54 : 6. 5. Найди произведение чисел 6 и 8. 6. Какое число больше 5 в 9 раз? 7. Уменьши 63 в 7 раз. 8. Найди частное ...Элементы математической логики
Луна – спутник Земли. 2) Информатика –это наука об информации и информационных процессах. 3) Монитор – это устройство ввода информации. 4) Процессор ...Полная и неполная индукция. Метод математической индукции
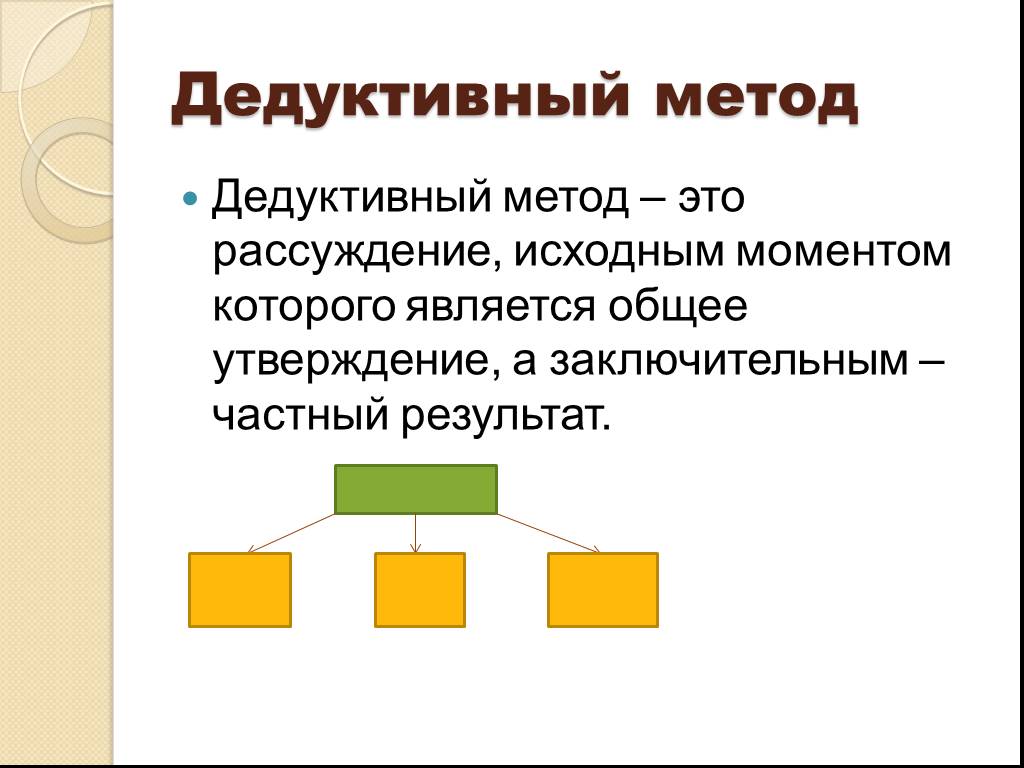
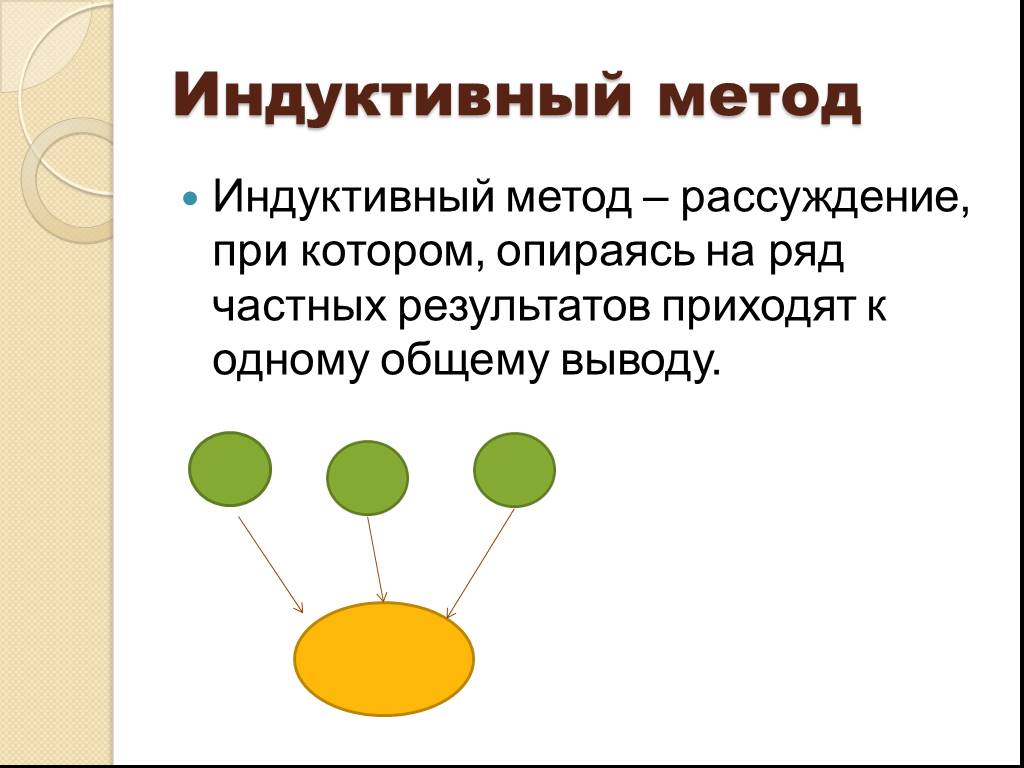
Дедуктивный и индуктивный метод В основе всякого математического исследования лежат дедуктивный и индуктивный методы. Дедуктивный метод рассуждений ...Требования к математической подготовке учащихся к началу основной школы
Основные содержательные линии. Арифметическая составляющая Умение работать с числами Умение работать с величинами Геометрическая составляющая. ...Метод математической индукции
Содержание: 1.Введение. 2.Основная часть и примеры. 3.Заключение. Введение В основе всякого математического исследования лежат дедуктивный и индуктивный ...Основы высшей математики и математической статистики
Учебники:. Н.Л. Лобоцкая и др. Высшая математика. Мн.1987г. Морозов Ю.В. Основы высшей математики и статистики. М. 1998г. И.В. Павлушков и соавт. ...История математической логики
ЭТАПЫ РАЗВИТИЯ ЛОГИКИ. Аристотель Рене Декарт Лейбниц Джордж Буль Последующее развитие логики. АРИСТОТЕЛЬ (384-322 ГГ. ДО Н.Э.) - ОСНОВОПОЛОЖНИК ЛОГИКИ. ...Вводный урок "Элементы математической статистики"
Термин «статистика» произошел от латинского слова «статус» (status), что означает «состояние и положение вещей». Математическая статистика. это наука, ...Базовые понятия математической статистики
Описательная статистика. Локализация Среднее значение Медиана Мода. Дисперсия Перцентиль Межквартильный размах Размах признака Дисперсия Стандартное ...Базовые понятия математической статистики
измерение есть присваивание чисел определенным объектам, свойствам, признакам, событиям или изменениям в соответствии с определенными правилами. психологические ...Элементы математической статиститки
Статистика – дизайн информации. Цель:. Дать понятие генеральной и выборочной совокупности, полигону и гистограмме частот Научиться строить полигон ...«Метод координат»
Координатный метод. Геометрия 9класс. Содержание. Координаты точки Расстояние между точками Уравнение окружности Координаты середины отрезка Уравнение ...Синус, косинус, тангенс и котангенс, алгебра,
Синус и косинус. Что будем изучать:. Определение синуса и косинуса. Определение тангенса и котангенса. Основное тригонометрическое тождество. Примеры ...Тригонометрические функции углового аргумента - алгебра,
Тригонометрическая функция углового аргумента. Что будем изучать:. Определение. Примеры. Вспомним геометрию. Градусная мера угла. Радианная мера угла. ...Матричная алгебра в экономике
Содержание:. ● Вступление ● Что такое матрицы и операции над ними ● Решение экономических задач матричным методом ● Заключение ● Список используемой ...Реляционная алгебра – механизм манипулирования реляционными данными
Две группы операций РА. теоретико-множественные операции специальные реляционные операции. Теоретико-множественные операции. объединения отношений; ...ГИА 2013. Модуль алгебра №6
ГИА – 2013 г. Модуль «Алгебра» №6. «ГИА-2013. Математика: типовые экзаменационные варианты: 30 вариантов» под редакцией А. Л. Семенова, И. В. Ященко. ...ГИА 2013. Модуль алгебра №8
Модуль «Алгебра» №8. Повторение (4). Решите неравенство 7+2(х-4)≥х+4. Ответ: [-3;+∞). Повторение (подсказка). При решении неравенства можно переносить ...Конспекты
Элементы теории вероятности и математической статистики
Управление образования г.Астаны. ИПК и ПК СО. ГУ «Средняя школа № 36». Урок алгебры в 9 классе по теме: «Элементы теории вероятности ...Элементы математической статистики и теории вероятности
Тема урока:. Элементы математической статистики и теории вероятности. Основные цели и задачи урока:. Повторить основные понятия изучаемого предмета: ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:2 мая 2019
Категория:Математика
Содержит:15 слайд(ов)
Поделись с друзьями:
Скачать презентацию