Презентация "Основные виды движений" по математике – проект, доклад
Презентацию на тему "Основные виды движений" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 13 слайд(ов).
Слайды презентации
Список похожих презентаций
Системы счисления. Основные определения, виды, свойства
ОПРЕДЕЛЕНИЯ. СИСТЕМА СЧИСЛЕНИЯ - совокупность приемов и правил для записи чисел. Коэффициенты - знаки (цифры), используемые для записи чисел. Наиболее ...Основные теоремы теории вероятностей
Литература и интернет - ресурсы. Вентцель Е.С., Овчаров Л.А. Задачи и упражнения по теории вероятностей: учебное пособие. М.: Академия, 2003. – 448 ...Основные свойства неопределенного интеграла
Доказательство:. 2. Дифференциал от неопределенного интеграла равен подынтегральному выражению. . 3. Неопределенный интеграл от дифференциала некоторой ...Треугольники и их виды
«Я думаю, что никогда до настоящего времени мы не жили в такой геометрический период. Всё вокруг – геометрия» Ле Корбюзье. Первичная актуализация. ...Тетраэдр, виды сечений и решение задач по тетраэдру
Цель работы:. Выяснить какие виды сечений тетраэдра существуют Терминология Показать на примерах решения задач тетраэдра. Терминология:. Тетраэдр ...Различные виды уравнения прямой
Общее уравнение прямой. Уравнение Ax+By+C=0 (где A, B и C могут принимать любые значения, лишь бы коэффициенты A, B не были равны нулю оба сразу) ...Призма: виды и особенности
План лекции.Понятие и чертёж Элементы призмы Общие свойства призм Виды призм и их особенности Поверхность призм Сечения призм Призмы вокруг нас. ...
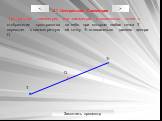
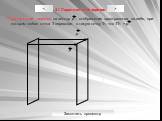
Основные фигуры в пространстве
Точка A. Прописные латинские буквы A, B, C, D, E, K, …. Прямая a. Строчные латинские буквы a, b, c, d, e, k, …. Плоскость α. Греческие буквы α, β, ...Ломаная , многоугольник и его виды
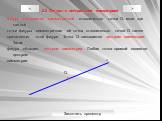
Ломаная. Ломаной A1A2... An называется фигура, которая состоит из упорядоченной совокупности точек и отрезков, соединяющих соседние среди них. Точки ...Логарифм. Основные понятия
. . . . Десятичные логарифмы. Логарифмы по основанию 10 (обозначение: lg a) до изобретения калькуляторов широко применялись для вычислений. Неравномерная ...Квадратные уравнения. Основные свойства
Из данных уравнений выбрать квадратные. А) х2 – 1 = 0; Б) х3 + 2х – 1 = 0; В) - 1 = 0;. Г) 3х = 0; Д) 2х2 – 5х + 6 = 0; Е) 7х – х2 + 3 = 0. ах2 + ...Квадратные и другие виды уравнений
Пифагор - очень важный кот. Гипа (Гипотенуза) – мудрая кошка, знает много историй. Шишок компьютерный – гид поисковик по Интернету. Гера – хозяин ...Движение и его виды
Начало движения. Задача По приглашению московские школьники в дни новогодних каникул посетят Англию. Найти кратчайшее расстояние от Москвы до Англии. ...Граф и его элементы. Основные определения
Переход по слайдам осуществляется только по нажатию левой кнопки мыши клик мыши!!! Если есть мигающая стрелка, значит нужно нажатие левой кнопки мыши ...Геометрия Основные темы
Данная презентация предназначена для проведения обобщающего урока по курсу геометрии 7 класс. Продолжительность показа презентации зависит от степени ...Основные тригонометрические формулы
Основные формулы тригонометрии и их свойства. Дадим определения тригонометрическим функциям синуса, косинуса, тангенса и котангенса. возьмем любой ...Основные труды и биография Декарта
Рене́ Дека́рт (31 марта 1596, Лаэ (провинция Турень) — 11 февраля 1650, Стокгольм) — французский математик, философ, физик и физиолог, создатель аналитической ...Многогранники: виды задач и методы их решения (типовые задания С2) - 2
Расстояние от точки до прямой, не содержащей эту точку, есть длина отрезка перпендикуляра, проведенного из этой точки на прямую. Расстояние между ...Основные формулы тригонометрии
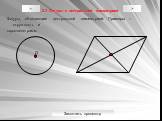
Содержание. Из истории… 2) Основные тригонометрические формулы а) основные тригонометрические тождества б) формулы сложения в) формулы суммы и разности ...Многоугольники и их виды
"Многоугольники"8 кл. Составные части многоугольников. Точки A, B, C, D, E являются вершинами многоугольника ABCDE Две вершины многоугольника, не ...Конспекты
Угол, виды углов
МУНИЦИПАЛЬНОЕ БЮДЖЕТНОЕ. ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ. СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА № 69. Учитель начальных ...Углы и их виды
Тема урока:. « Углы и их виды». Учитель математики: Хамитова В.З. Цели урока:. Образовательные. Систематизировать знания и умения учащихся, ...Угол и его виды
Конспект урока по математике в 1 – б классе. . учителя начальных классов МБОУ «СОШ №14». г. Донской Тульской области. Агаповой Светланы Серафимовны. ...Основные приемы решения задач на сплавы, смеси, растворы
Афанасьева Елена Викторовна. МБОУ СОШ№12, г.Ноябрьск. учитель математики. . Тема:. . «Основные приемы решения задач на сплавы, смеси, растворы». ...Треугольники и их виды
Тема урока «Треугольники и их виды». Цели. : научить выделять признаки различных видов треугольников, объединять треугольники по группам на основе ...Основные методы решения тригонометрических уравнений
. МАТЕМАТИКА 11 класс. Тема: Основные методы решения тригонометрических уравнений. Цели урока:. Обобщить и систематизировать полученные знания ...Квадратные уравнения. Основные понятия. Решение неполных квадратных уравнений
Тема:. «Квадратные уравнения. Основные понятия. Решение неполных квадратных уравнений». Тип урока:. урок изучения нового материала. Цели урока:. ...Задачи на разные виды движения двух тел в противоположных направлениях
Технологическая карта урока. Учебный предмет. :. математика. . Класс:. 4 класс. . . Тема. урока. :. «Задачи на разные виды движения двух ...Действия с обыкновенными дробями. Основные задачи на дроби
ГБС(К)ОУ ШИ. I. -. II. вида г. Тихорецка Краснодарского края. Урок – КВН. в 7 классе по теме:. «Действия с обыкновенными дробями. Основные ...Выражения: виды, особенности выражений
Краткосрочное планирование. Предмет:. математика. Класс:. 4. Дата проведения: 30.04.2013 г. Занятие: 2. Тема урока: Выражения: виды, особенности ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:26 апреля 2019
Категория:Математика
Содержит:13 слайд(ов)
Поделись с друзьями:
Скачать презентацию