Презентация "Прямоугольник, ромб, квадрат" по математике – проект, доклад
Презентацию на тему "Прямоугольник, ромб, квадрат" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 13 слайд(ов).
Слайды презентации
Список похожих презентаций
Параллелограмм, прямоугольник, ромб, квадрат
Цели урока. Обобщение и систематизация знаний и умений учащихся по данной теме, решение задач с использованием свойств параллелограммов Развитие умений ...Прямоугольник
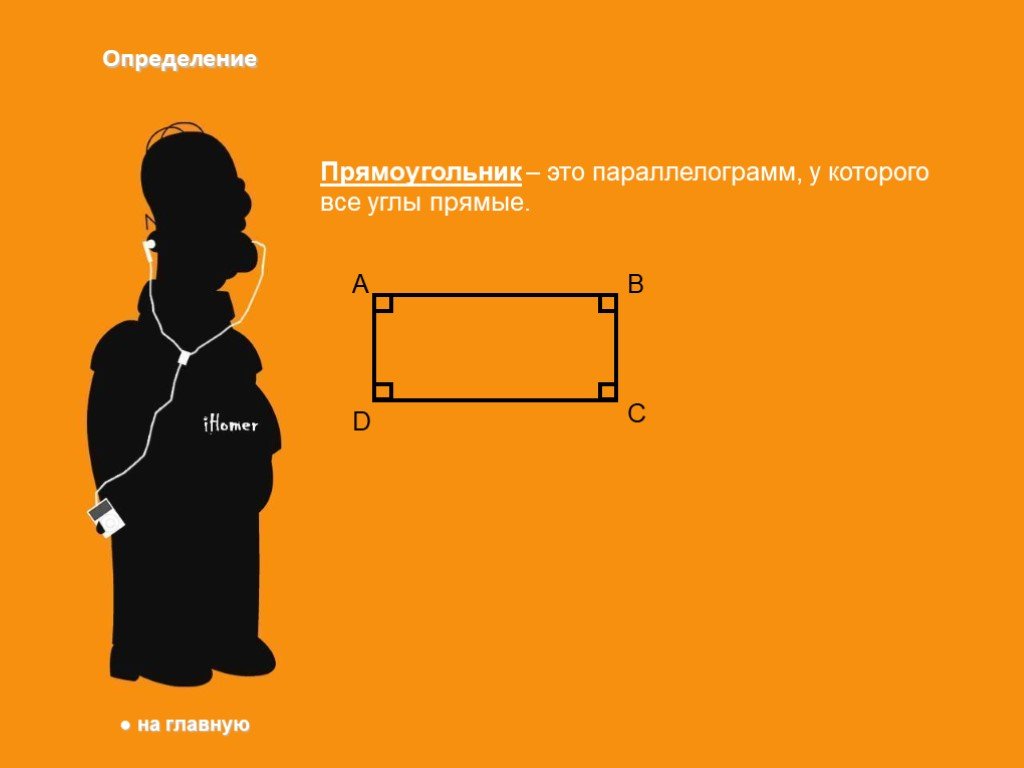
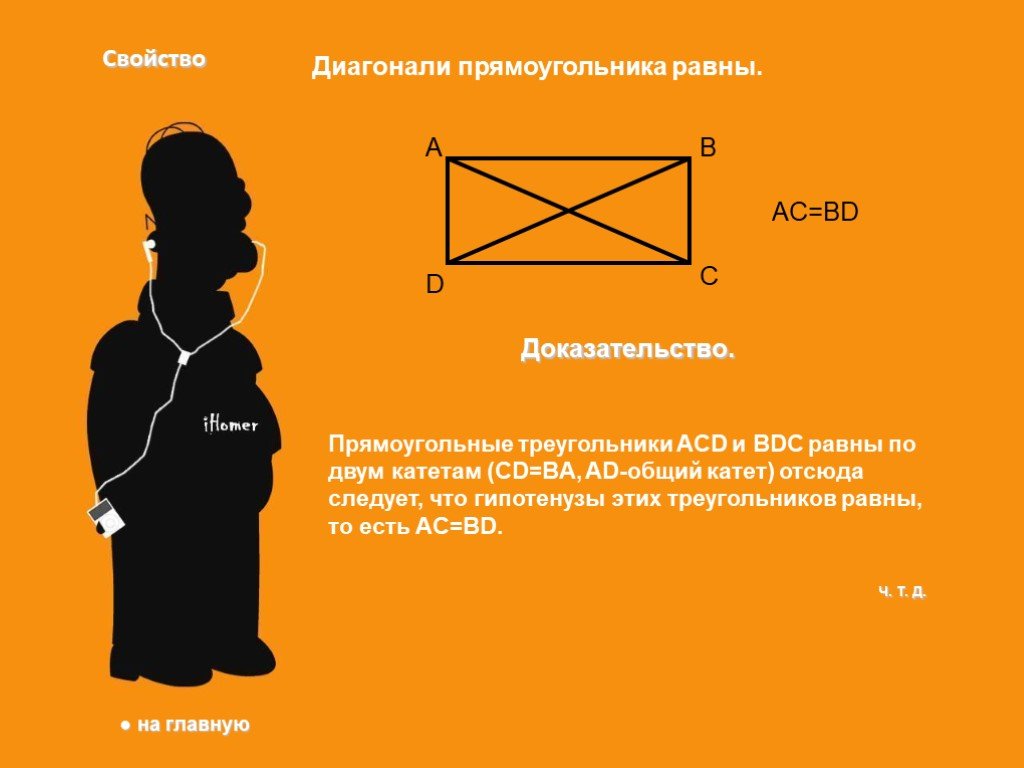
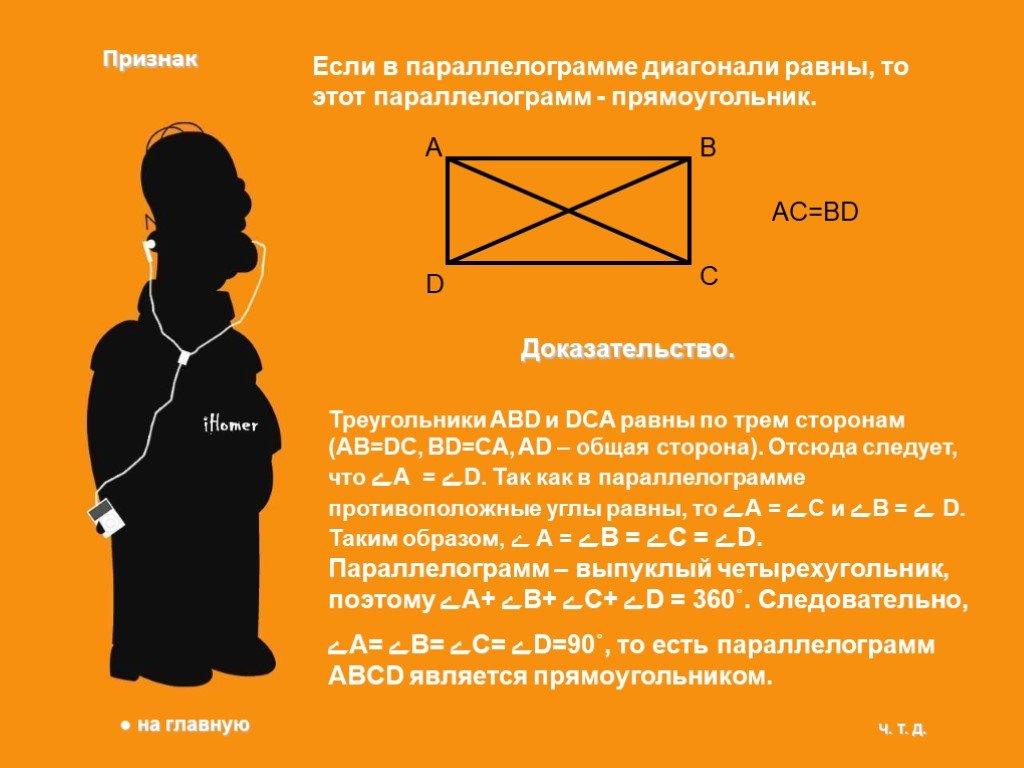
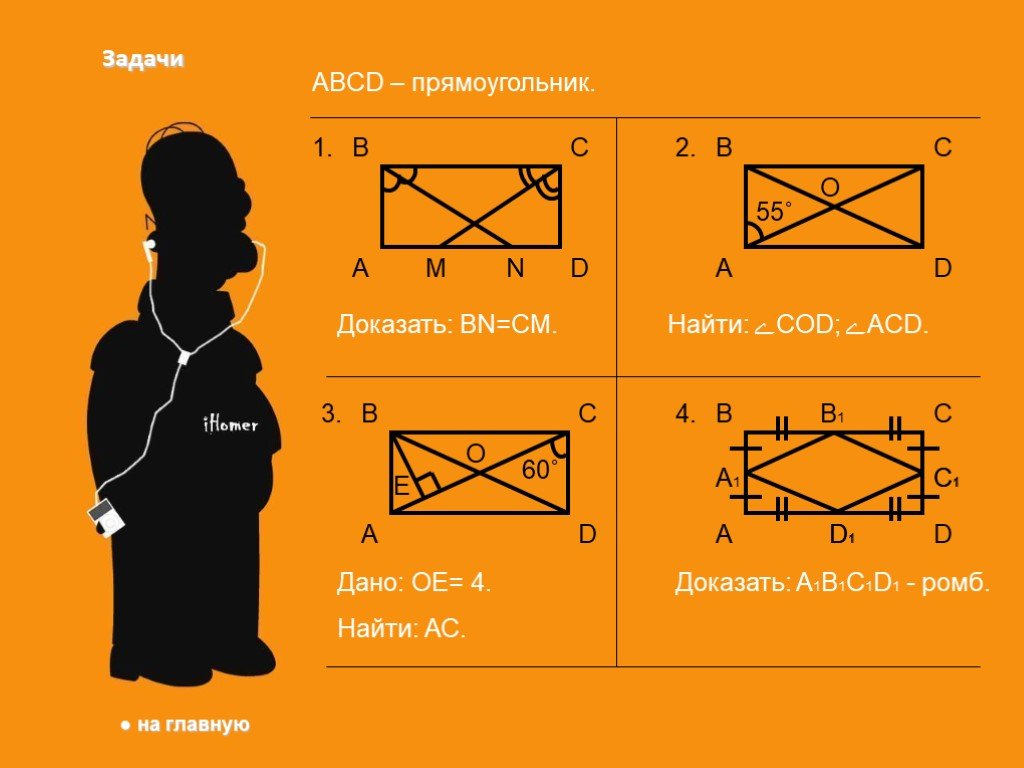
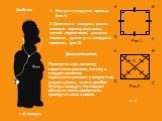
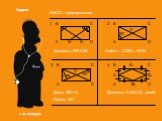
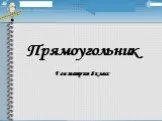
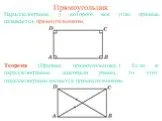
Если вы увидите параллелограмм, у которого все углы равны, знайте что это прямоугольник. Свойства прямоугольника. 1.Все 2.Про- з.Сумма 4.Диагонали ...Прямоугольник
1. Какая фигура называется четырёхугольником? 2. Какие стороны четырёхугольника называются противоположными? 3. Дайте определение параллелограмма. ...Почему квадрат?
КВАДРАТ. Это квадрат или прямоугольный четырехугольник, все стороны равны, а все четыре угла - прямые. ПРЯМОУГОЛЬНИК. А это прямоугольник. У прямоугольника ...Магический квадрат
Задачи:. выяснить происхождение магических квадратов; научиться составлять такие квадраты; провести опрос окружающих, что они знают по этому вопросу. ...Квадрат суммы и квадрат разности двух выражений
Игра «Третий лишний». 3² 9 6 4а² 16а² (4а)² (а + b)² (a + b)(a + b) a² + b² (c – d)² (c – d)(c + d) (c – d)(c – d) (7 – 3)² 16 40 (– a)² a² – a² (a ...Квадрат суммы, квадрат разности
Прочитай выражения. Продолжи формулу и прочитай её. Продолжим. Раскройте скобки. В классе: №817( в, д), 819(а, б), 821(а, б) Дом. задание: 817(а, ...Квадрат суммы и квадрат разности
. . . . . . . . . . . . . . . . . ...Квадрат суммы и квадрат разности
По какому признаку можно провести классификацию данных выражений на 2 группы? I )(7-b)(7+b) II) (x+y)(x+y) III) (4-a)(4-a) IV ) (c-6)(c-6) V) (m-x)(m-x) ...Волшебный квадрат
-рассказать об истории развития магических квадратов, -рассмотреть свойства магического квадрата 4-ого порядка -уметь составлять магический квадрат ...Какому числу равен квадрат числа 11
Какому числу равен куб числа 8 а)24; б)64; в)512. Укажите верное равенство а)32=22; б)82=42; в)104=1002. Квадратом какого числа является число 225? ...Возведение в степень. Куб и квадрат числа
Устно. Упростить выражение: 25х + 15 х; 12у – 3у; 9k + 9k – 4k; 80c-35c-14c; 8d+d-9d; 163 + 37v + 18v. Решить уравнение: 7х+2х = 918; 5а-3а = 222; ...Возведение в квадрат суммы и разности двух выражений.
«Слабое звено». 1. Вычислите: 52 ; 23; (-5)3 ; (-8)2 ; 112 ; 0,32 ; 1,52. 2. Представьте в виде многочлена: (х+у)2; (m-n)2; (х-5)2; (2х+3)2; (5n+3)2; ...Возведение в квадрат суммы и разности двух выражений
ВОЗВЕДЕНИЕ В КВАДРАТ СУММЫ И РАЗНОСТИ ДВУХ ВЫРАЖЕНИЙ. ТЕМА УРОКА. Образовательные: -вывести формулы квадратов суммы и разности двух чисел; -сформировать ...Прямоугольник
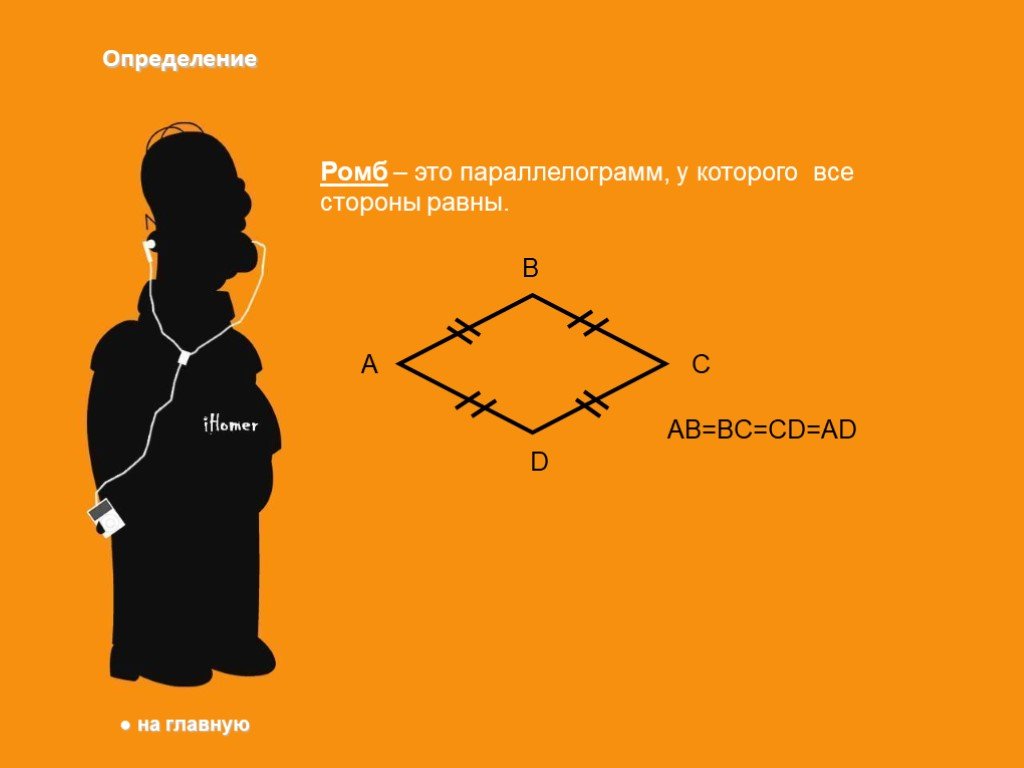
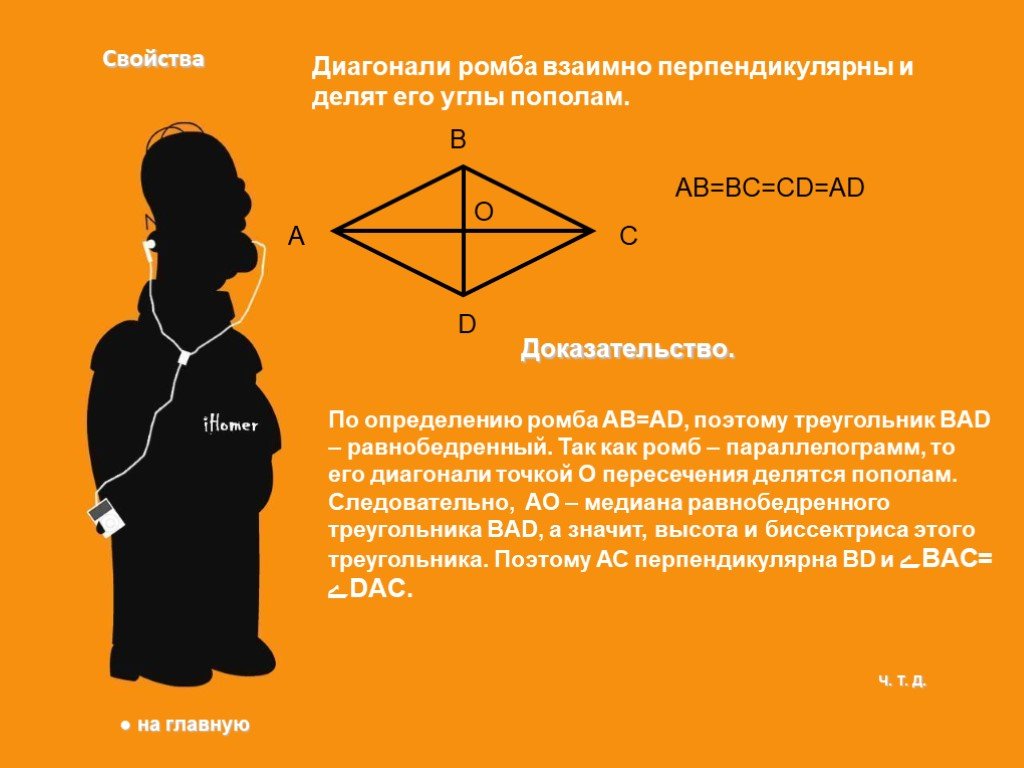
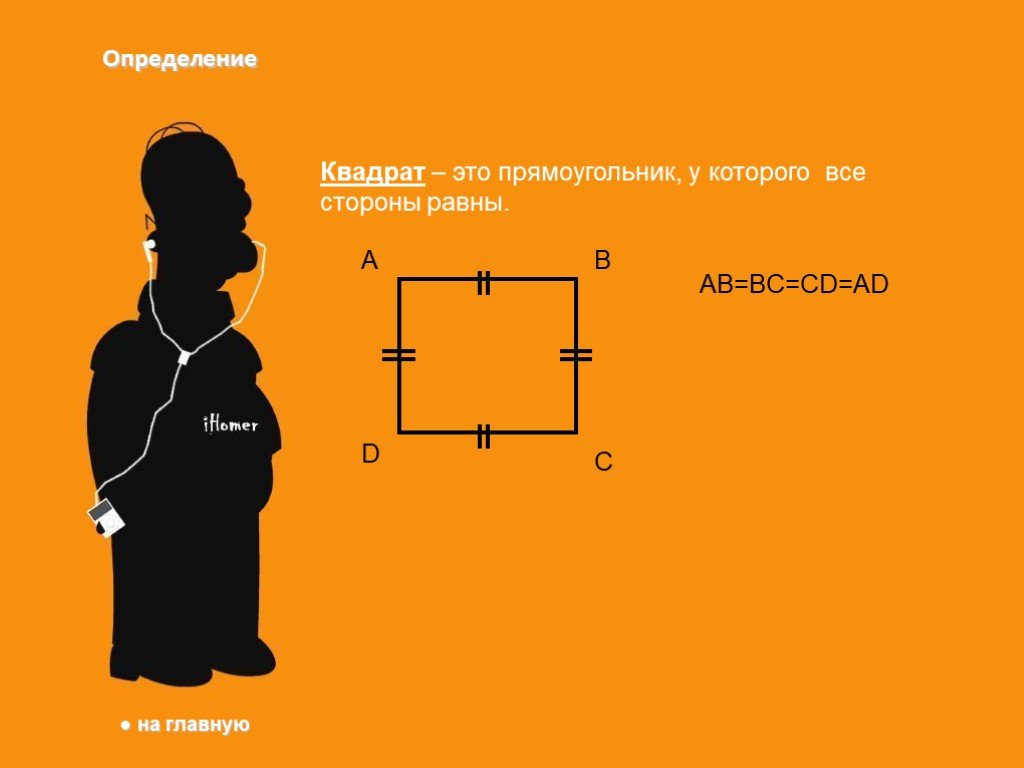
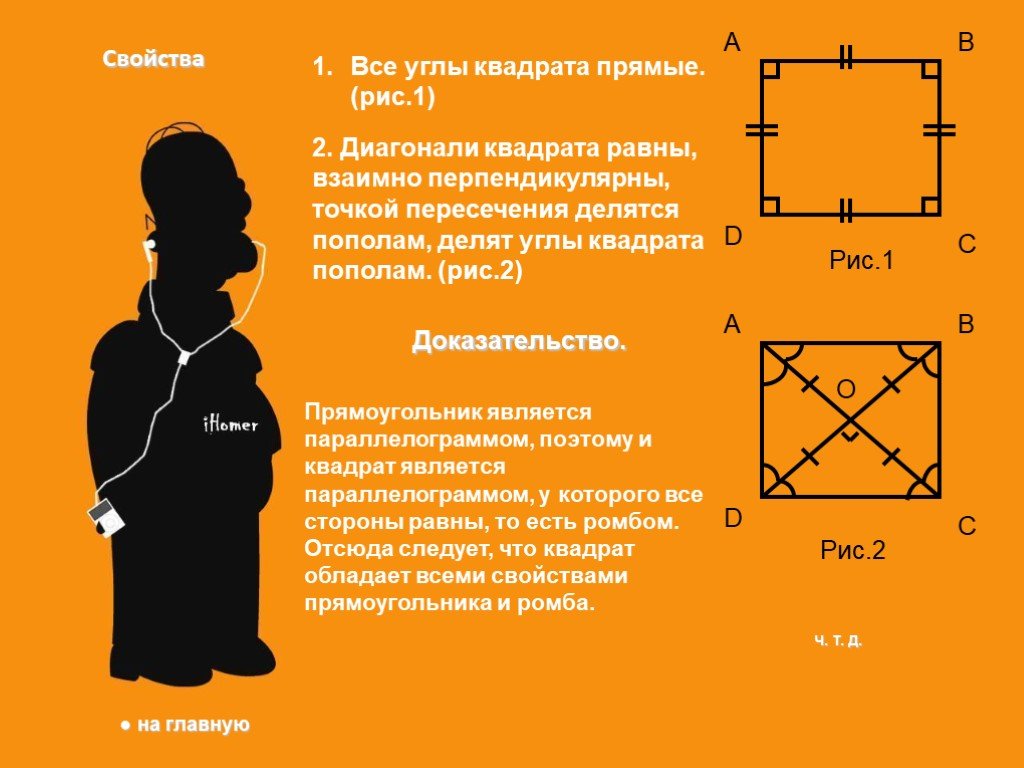
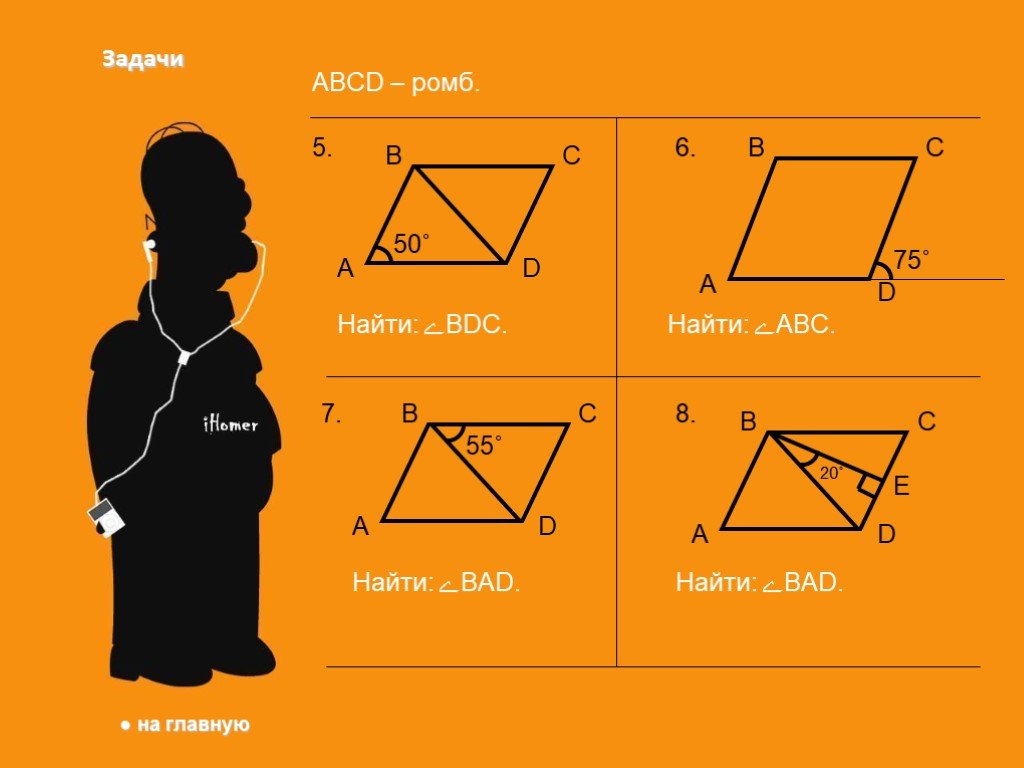
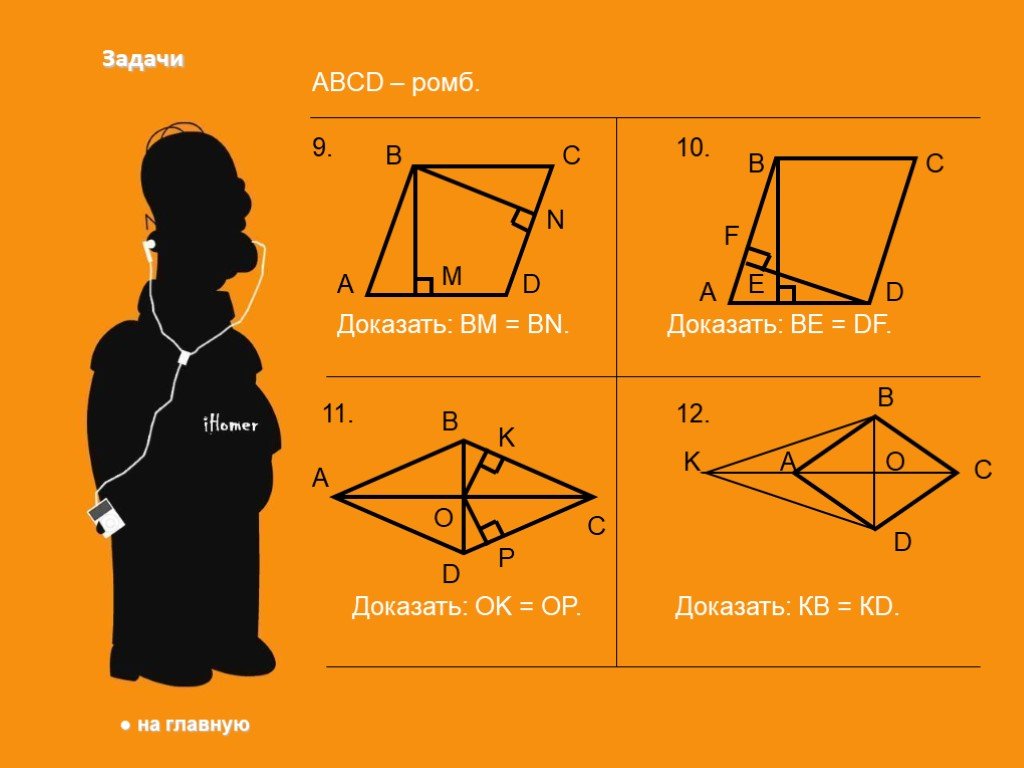
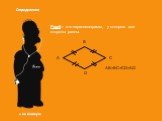
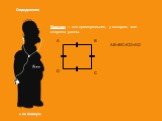
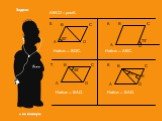
Ромб. Параллелограмм, у которого все стороны равны, называется ромбом. Квадрат. Прямоугольник, у которого все стороны равны, называется квадратом. ...Прямоугольник
Разность чисел 12 и 3 уменьшите на 5. е. К сумме чисел 7 и 8 прибавьте 3. м. Найдите периметр прямоугольника со сторонами 5 и 2 см. г. Уменьшаемое ...Возведение в квадрат суммы и разности двух выражений
Из истории Древнего мира. Среди математиков Древней Греции было принято выражать алгебраические утверждения в геометрической форме. Вместо сложения ...Возведение в квадрат суммы и разности двух выражений
ЦЕЛЬ: пользуясь правилом умножения многочленов, провести исследовательскую работу и вывести формулы (а±в)²=а²±2ав+в²; привитие навыка самостоятельной ...Геометрия Евклида и геометрия Лобачевского. Сходства и отличия
Евклидова геометрия. Евкли́д или Эвкли́д (, ок. 300 г. до н. э.) — древнегреческий математик. Мировую известность приобрёл благодаря сочинению по ...Все вокруг - геометрия
Откуда есть, пошла «Геометрия»? Слово «геометрия» - греческое, в переводе на русский означает «землемерие». около 4000 лет тому назад жители Древнего ...Конспекты
Параллелограмм, прямоугольник, ромб, квадрат и их свойства
. Муниципальное общеобразовательное учреждение. Новолядинская средняя. . общеобразовательная школа. Тамбовского района Тамбовской области. ...Квадрат суммы и квадрат разности
Муниципальное казенное общеобразовательное учреждение. лицей №11 г.Россошь Россошанского района. Воронежской области. . . Открытый урок ...Квадрат суммы, квадрат разности, умножение разности двух выражений на их сумму
Иванова Марина Викторовна. МАОУ СОШ № 54 г. Томск. Учитель математики. Обобщающий урок по теме. «Квадрат суммы, квадрат разности, умножение ...Десяток. Состав чисел в пределах 10. Прямоугольник
МКС(К)ОУ для обучающихся, воспитанников с ограниченными возможностями здоровья Еманжелинская специальная (коррекционная) школа-интернат VIII вида. ...Квадрат суммы и квадрат разности
План-конспект урока. . ФИО (полностью). . Облакова Ирина Анатольевна. . . . Место работы. . Муниципальное бюджетное общеобразовательное ...Геометрические фигуры - круг и квадрат
Муниципальное казённое дошкольное образовательное учреждение компенсирующего вида «Детский сад №1», Лесная сказка. Нижегородской области г. Саров. ...Возведение в квадрат суммы и разности двух выражений
МКОУ «Гавриловская средняя общеобразовательная школа». Учитель математики Панкратова Нина Владимировна. ПЛАН-КОНСПЕКТ УРОКА ПО АЛГЕБРЕ 7 КЛАСС. ...Возведение в квадрат суммы и разности двух выражений
Кудрявцева О.А., учитель математики МБОУ «Средняя общеобразовательная школа №15» г. Калуги. . Возведение в квадрат суммы и разности двух выражений. ...Возведение в квадрат суммы и разности двух выражений
Голубцова Ирина Николаевна. МБОУ «СОШ № 4» с. Сотниковское. Учитель математики. Урок по алгебре. 7 класс. Тема:. «Возведение в квадрат ...Возведение в квадрат и в куб суммы и разности двух выражений
Конспект урока алгебры по теме:. «Возведение в квадрат и в куб суммы и разности двух выражений». 7класс. Учитель математики. Гнутова ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:9 января 2019
Категория:Математика
Содержит:13 слайд(ов)
Поделись с друзьями:
Скачать презентацию