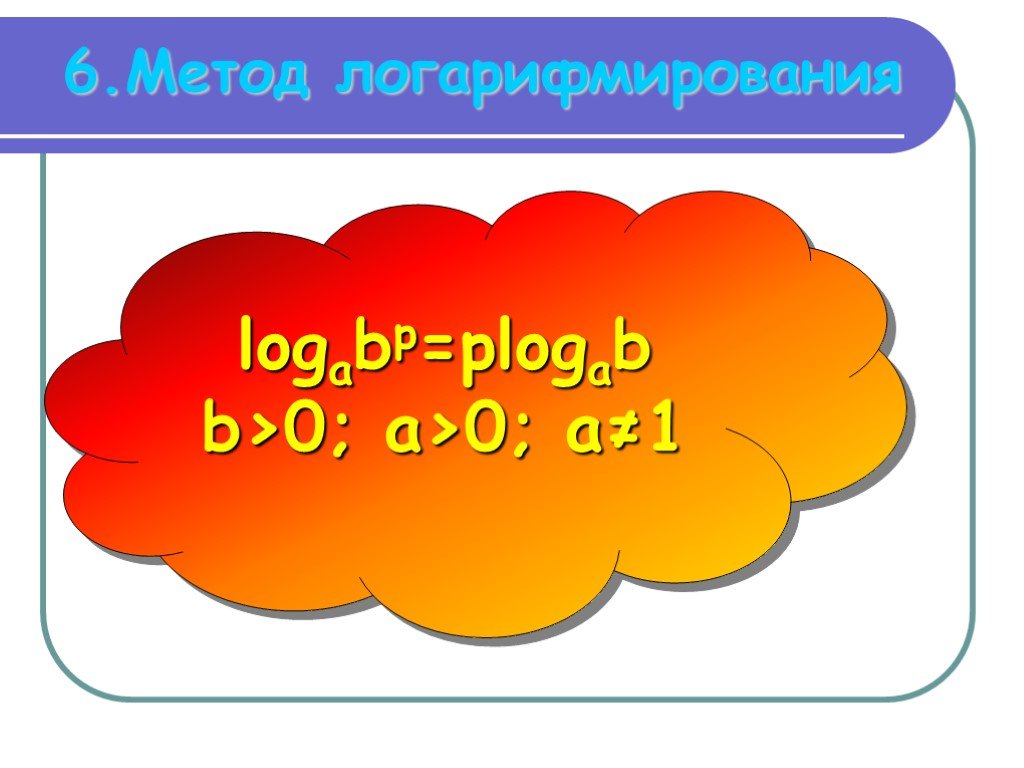
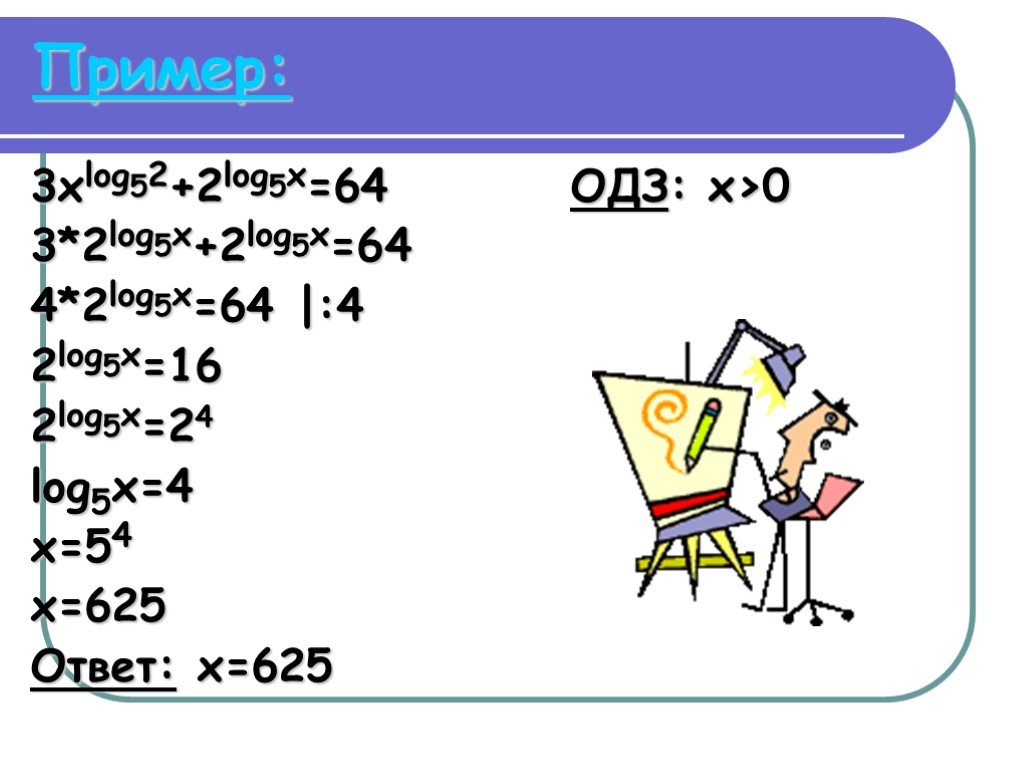
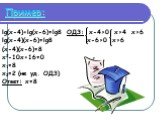
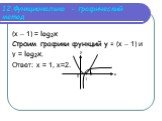
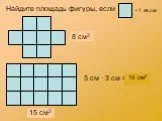
Презентация "Логарифмические уравнения" по математике – проект, доклад
Презентацию на тему "Логарифмические уравнения" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 26 слайд(ов).
Слайды презентации
Список похожих презентаций
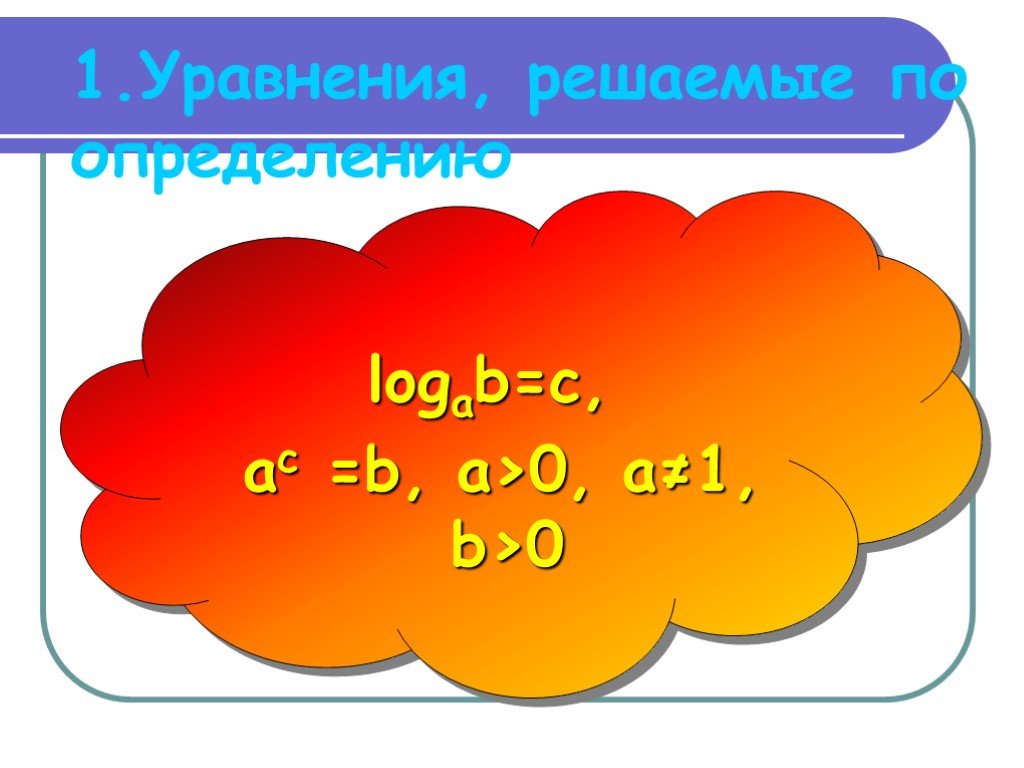
Логарифмические уравнения
Математик Джон Бригг, прославившись открытиями в области логарифмов писал:. «Своими новыми и удивительными … уравнениями Непер заставил меня усиленно ...Логарифмические уравнения и их системы
Функция y = loga х (где а > 0, а =1) называется логарифмческой. График логарифмической функции logaх можно построить, воспользовавшись тем, что функция ...Урок Логарифмические уравнения
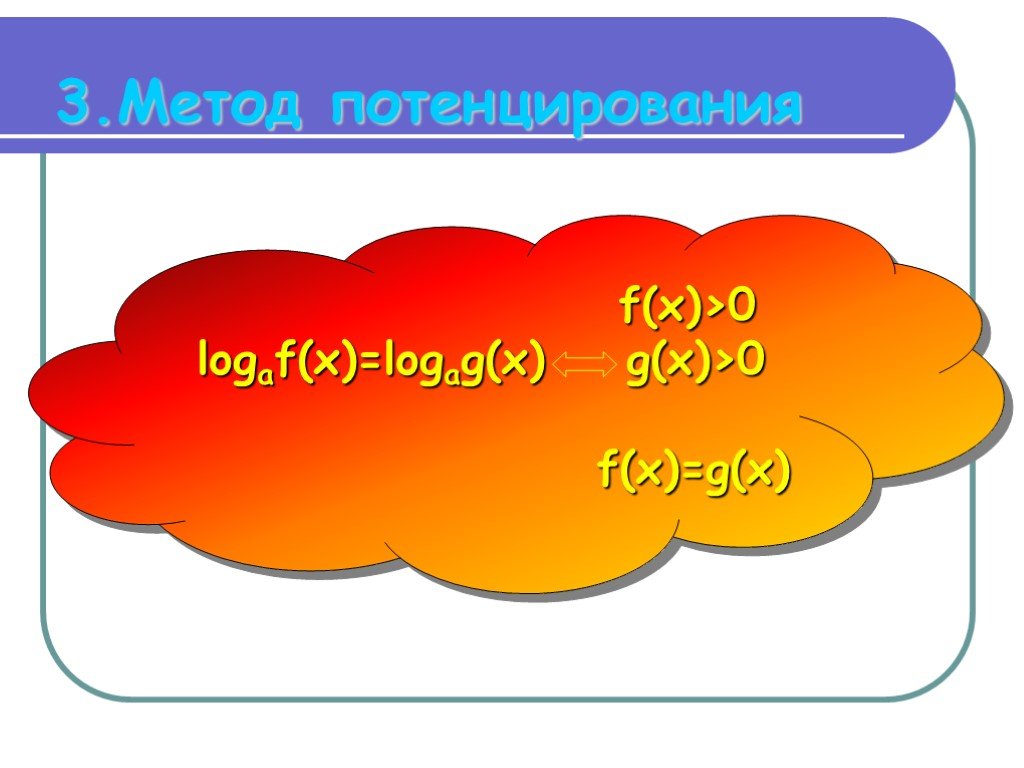
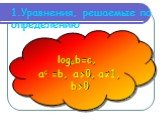
logax = b x > 0 a > 0 a ≠ 1. НАЙДИТЕ ОБЛАСТЬ ДОПУСТИМЫХ ЗНАЧЕНИЙ УРАВНЕНИЙ. 1.logx5 = 1 2.logx(x2-1) = 0 3.log5(2x+1) = log5(x+2). ОПРЕДЕЛИТЕ МЕТОДЫ ...Логарифмические уравнения
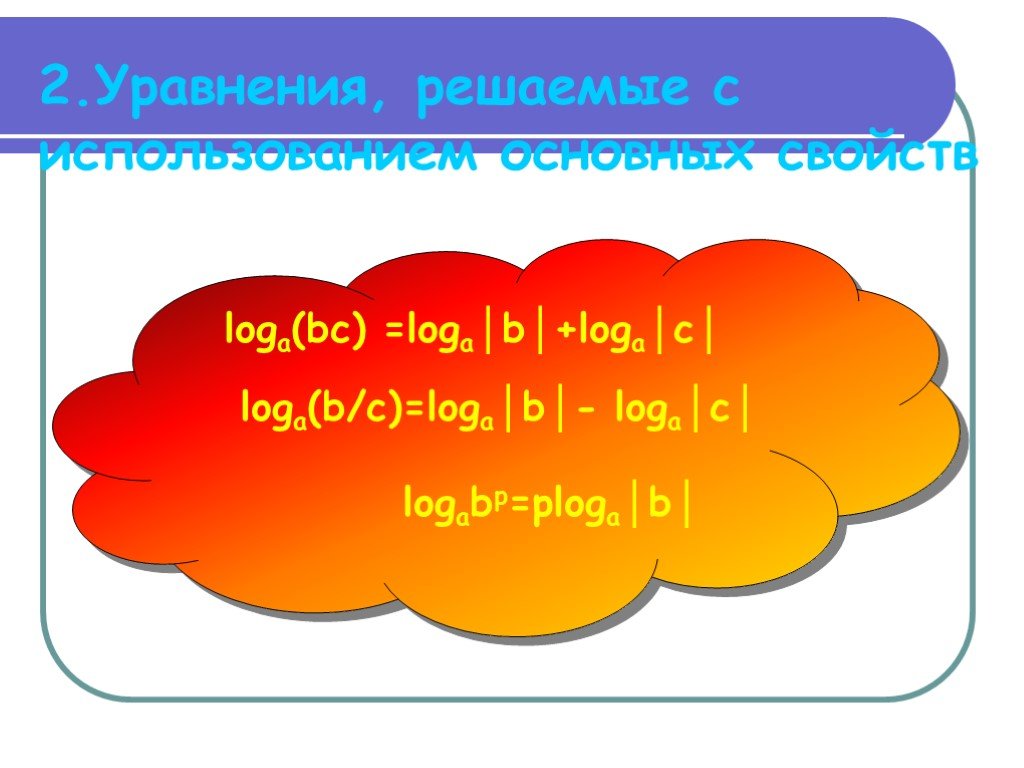
Определение логарифма Об истории развития логарифмов Основные свойства логарифмов (Формулы преобразования логарифмов) О монотонности логарифмической ...Логарифмические уравнения и неравенства
Цель урока. Повторение свойств логарифмов и логарифмической функции. Отработка навыков при решении логарифмических уравнений и неравенств. Определение ...Многочлены и уравнения высших степеней
Пояснительная записка. За минувший век в математике произошли грандиозные изменения, она (впрочем, как и все другие науки) шагнула необыкновенно далеко ...Формула корней квадратного уравнения
Сегодня на уроке мы будем:. записывать квадратные уравнения; вспоминать формулы нахождения корней квадратного уравнения; решать квадратные уравнения ...Тригонометрические уравнения
Тригонометрические уравнения. Уравнение представляет собой наиболее серьёзную и важную вещь в математике. О.Лодж. «Дороги не те знания, которые откладываются ...Решение уравнений в целых числах. Диофантовы уравнения
Диофантовы уравнения. Алгебраические уравнения с целыми коэффициентами, решаемые во множестве целых чисел, вошли в историю математики как диофантовы. ...Простейшие тригонометрические уравнения
История развития тригонометрии. . . . . . . . . . . Устная работа. Ответьте на вопросы:. Может ли косинус быть равным: 0,75; 5/3; -0,35; π/3; 3/π; ...Показательные уравнения и способы их решения
Определение: Показательные уравнения – уравнения, в которых переменная входит только в показатели степеней при постоянных основаниях. Например,. Основные ...Показательные уравнения
Показательные. Цели урока: 1. ввести понятие показательных уравнений; 2. формировать умение решать показательные уравнения основными методами: функционально-графическим, ...Диофантовы уравнения
Цели и задачи. Определение диофантова уравнения Биография Диофанта Диофантовые уравнения первой степени Диофантовые уравнения высших степеней Проект ...Диофантовы уравнения
СКОЛЬКО РЕШЕНИЙ ИМЕЕТ ДАННОЕ УРАВНЕНИЕ? (2х+у)(5х+3у)=7. 3) Не имеет решений. 4) Бесконечно много решений. Следующее задание. (3х+7у)(х-у)=13 1) 2 ...Диофантовы уравнения
Диофантовы уравнения Глобально не изучаются в школьной программе, а присутствуют на экзамене! Проблема подтолкнувшая на создание работы:. обусловлена ...Диофантовы уравнения
Цели учебно – исследовательской работы: изучить способы решения диофантовых уравнений; повысить уровень математической культуры, прививая навыки самостоятельной ...Графическое решение линейного уравнения с двумя переменными
Цель урока:. проверить прочность знаний, умений и навыков, учащихся по данной теме, обеспечить закрепление и обобщение изученного материала; развивать ...Графики линейного уравнения с двумя переменными
Цель урока:. ввести понятие графика уравнения с двумя переменными; повторить построение графика линейной функции по двум точкам; закрепить навыки ...Обыкновенные дифференциальные уравнения
Уравнение первого порядка. Функциональное уравнение F(x,y,y) = 0 или y= f(x,y), связывающее между собой независимую переменную, искомую функцию ...Определение квадратного уравнения. Неполные квадратные уравнения
ax+b=0. 1) (2х-3)2-2х(4+2х)=49, 2) y2+80=81, 3) -z+4=47, 4) 2x2+3х+1=0, 5) 4k/3+4=k/2+1, 6) 12s-4s2=0, 7) 10+p2-4p=2(5-3p), 8) 6(t-1)=9,4-1,7t, 9) ...Конспекты
Логарифмические уравнения решаемые с помощью квадратных уравнений
Министерство образования и науки Республики Казахстан. Атбасарский районный отдел образования. Акмолинской области. Открытый урок по алгебре ...Логарифмы. Логарифмические уравнения
. Конспект урока. . по алгебре и началам анализа. . по теме: «Логарифмы. . . Логарифмические уравнения». в 11 классе. Учитель: Щёкина ...Логарифмические уравнения и неравенства
Тема. : «Логарифмические уравнения и неравенства». Цели: Проверить теоретические и практические знания по теме; отработать навыки решения логарифмических ...Логарифмические уравнения и способы их решения
. План-конспект урока по теме:. «Логарифмические уравнения и способы их решения» (10 кл.). Автор:. Филиппова Е.М.,. учитель МБОУ СОШ №1. ...Логарифмические уравнения
Тема:. Урок систематизации и обобщения знаний по теме «Логарифмические уравнения». Класс:. 11. Учитель:. . Гомбоева Самажаб Бадмаевна, учитель ...Логарифмические уравнения
План урока алгебры в 11 классе. Тема урока: Логарифмические уравнения. Цели урока. :. . - образовательные. : систематизировать знания по ...Логарифмические уравнения
Логарифмические уравнения. 11 класс. Алгебра и начала анализа. А.Г.Мордкович. Цели урока:. Обучающие:. повторить методы решения логарифмических ...Свойства логарифмов. Логарифмические и показательные уравнения и неравенства
Муниципальное бюджетное образовательное учреждение. . «Средняя общеобразовательная школа № 7» им. О.Н. Мамченкова. . г. Елизово, Камчатский край. ...Повторение: логарифмы, логарифмические уравнения
Преподаватель: Гаученова Валентина Петровна. Забайкальский край. Государственное профессиональное образовательное учреждение «Чернышевское многопрофильное ...Показательные уравнения
ТЕМА «Показательные уравнения». Цели:. 1.Познакомиться с разными видами показательных уравнений, научиться различать разные виды показательных уравнений, ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:23 мая 2019
Категория:Математика
Автор презентации:Учитель математики: О.С. Чупрова
Содержит:26 слайд(ов)
Поделись с друзьями:
Скачать презентацию