Презентация "Использование компьютерной программы «Математика»" – проект, доклад
Презентацию на тему "Использование компьютерной программы «Математика»" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 26 слайд(ов).
Слайды презентации
Список похожих презентаций
Использование тригонометрической окружности при решении тригонометрический уравнений
Вычислите устно. Назвать положительный корень уравнения. Найти наименьший положительный корень. . . Найти наибольший отрицательный корень. . . Наибольшее ...Использование статистических методов при изучении отношения школьников к математике
Цель исследования: выявить с помощью статистических методов отношение учащихся к математике. Задачи исследования: изучить историю и методы статистики; ...Использование схемы анализа на уроках математики и литературы
Буква и цифра, Слово и число, Словесность и математика… - две формы общения человека с миром. Слово – Бог… Математика – Королева наук… Так ли они ...Использование алгоритмов при решении примеров, уравнений и задач
4 5 10 16 18 27 400 560 Г л и А Т М О Р. Алгоритм умножения на трёхзначное число. 1. Число умножаем на единицы 2. Число умножаем на десятки 3. Число ...Использование системно-деятельностнoго подхода на уроках математики
Б.Ф.Ломов Б.Г.Ананьев А.Н. Леонтьев Л.С.Выготский Л.В.Занков Д.Б.Эльконин В.В.Давыдов. В основе Стандарта лежит системно-деятельностный подход, который ...Путешествие по стране «Математика»
Блиц - турнир для 7 (1)класса. 1) Сколько получится если разделить полсотни на половину? (50:1/2=100) 2) Даны числа 0,1,2,…,9. Что больше: их сумма ...Система компьютерной алгебры GAP
Как расшифровать “GAP” ? Groups Algorithms Programming. Что такое GAP ? Компьютерная алгебра – современная область науки, возникшая на стыке математики ...Использование информационно- педагогических технологий на уроках математики
Цель участия в конкурсе «Мастер класс». Формирование представлений об использовании ИКТ на уроках математики при изучении вопросов теории вероятностей ...Использование информационных технологий на уроках математики
Информационные технологии. Под термином "информационные технологии" понимаются процессы накопления, обработки, представления и использования информации ...Использование игровых моментов при повторении на уроках математики в 5-ых классах
Здравствуйте детишки! Меня зовут Сережа и я хочу попросить у Вас помощи. У меня убежал щенок! Помогите мне его найти! Чтобы помочь найти щенка нам ...Использование интерактивной доски при обучении математике
"Человеческая жизнь — это борьба между невежеством и просвещенностью, просветлением… Как только человек прекращает искать информацию и знания для ...Использование здоровьесберегающих технологий на уроках математики
“Забота о здоровье – это важнейший труд воспитателя. От жизнедеятельности детей зависит их духовная жизнь, мировоззрение, умственное развитие, прочность ...Использование графов в решении логических задач
ГРАФЫ. Графами называются геометрические фигуры, состоящие из точек (вершин графа) и линий (ребер графа), соединяющих эти точки. При этом с помощью ...Использование геометрических фигур в реальной жизни
. Произведение инженерного искусства. Египетские пирамиды. . Одно из самых высоких зданий в Европе. Мост. Разводной мост. Одно из самое больших колес ...Использование умножения одночлена и многочлена при преобразовании алгебраических выражений и решении уравнений
Цель: рассмотреть практическое применение одночленов и многочленов при выполнении различных действий. Найди одночлены и многочлены. 3 х(-5)у 0,4+а ...Использование компьютерных технологий на уроках алгебры и геометрии
Творчество есть не более как проекция детских качеств на жизнь взрослых,… если бы процессы, с которыми они связаны, удивление и любопытство, тяга ...Использование элементов технологии самосовершенствования личности на уроках математики в классах коррекционно – компенсирующего обучения
По данным НИИ детства, ежегодно рождается 5 - 8℅ детей с наследственной патологией, 8 – 10 % имеют выраженную врождённую или приобретенную патологию, ...Использование национально-регионального компонента в обучении математике
Примеры таких задач. Территория Баймакского района составляет примерно 5432кв.км 1)переведите его в кв.метры 2)число 5432 округлите до десятков, до ...Реализация требований ФГОС средствами предмета «Математика»
Цели изучения математики. Математическое развитие младшего школьника Освоение начальных математических знаний Развитие интереса к математике. Место ...Использование параллелограмма в жизни
Параллелограмм в жизни –. – это рамы велосипедов, мотоциклов, где для жесткости проведена диагональ. В физике параллелограмм применяют при изучении ...Конспекты
Уменьшаемое. Вычитаемое. Разность. Использование этих терминов при чтении записей
1 «Б» класс Юрченко А.В. 9.04.2013г. Открытый урок на семинаре. . . Урок математики по теме:. "Уменьшаемое. Вычитаемое. Разность. Использование ...Таблица разрядов и классов. Использование таблицы разрядов и классов для выполнения действий сложения и вычитания
Проект урока по УМК «Перспективная начальная школа». Учитель: Емельянова Ольга Валентиновна. МОУ «Средняя общеобразовательная школа №9». ...Уменьшаемое, вычитаемое,разность. Использование этих терминов при чтении чисел
Муниципальное бюджетное общеобразовательное учреждение. «Мурманская средняя общеобразовательная школа». Конспект урока по математике. ...Слагаемые. Сумма. Использование этих терминов при чтении записей
Автор: Мизеркова Елена Владимировна. Место работы: МКОУ Октябрьская СОШ Мантуровского района Костромской области. Должность: учитель начальных классов. ...Способы решения квадратного уравнения. Использование частных соотношений коэффициентов
Урок в 8 классе по алгебре с применением технологии критического мышления в процессе преподавания математики. Тема: «Способы решения квадратного ...Вводный урок. Повторение программы 7 класса
Государственное бюджетное общеобразовательное учреждение. средняя общеобразовательная школа №625. с углублённым изучением математики Невского района ...Нестандартные методы решения уравнений и неравенств. Использование области определения функций
Тема урока: Нестандартные методы решения уравнений и неравенств. Использование области определения функций. . ФИО (полностью). . Кривошеин ...Использование прогрессий для решения задач
Пашина Л. В. ГБОУ гимназия №399, Санкт-Петербург. Использование прогрессий для решения задач. Предлагаю вашему вниманию урок, который я провожу ...Использование свойства арифметического корня
Тема: «Использование свойства арифметического корня». Цели:. . 1.Закрепление навыков использования свойств арифметического квадратного корня ...Использование монотонности при решении уравнений
Тема урока:. Использование монотонности при решении уравнений. Класс: 11. Время. : 1 урок (45 минут). Тип урока:. урок-мастерская. Необходимое ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:28 сентября 2019
Категория:Математика
Содержит:26 слайд(ов)
Поделись с друзьями:
Скачать презентацию

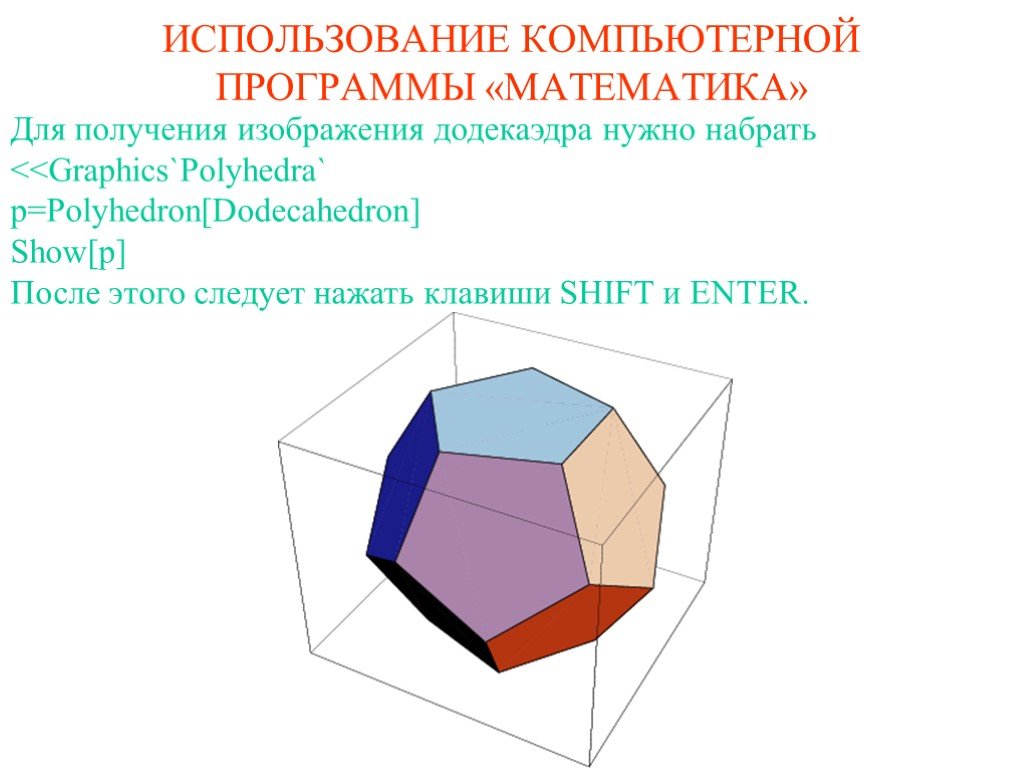

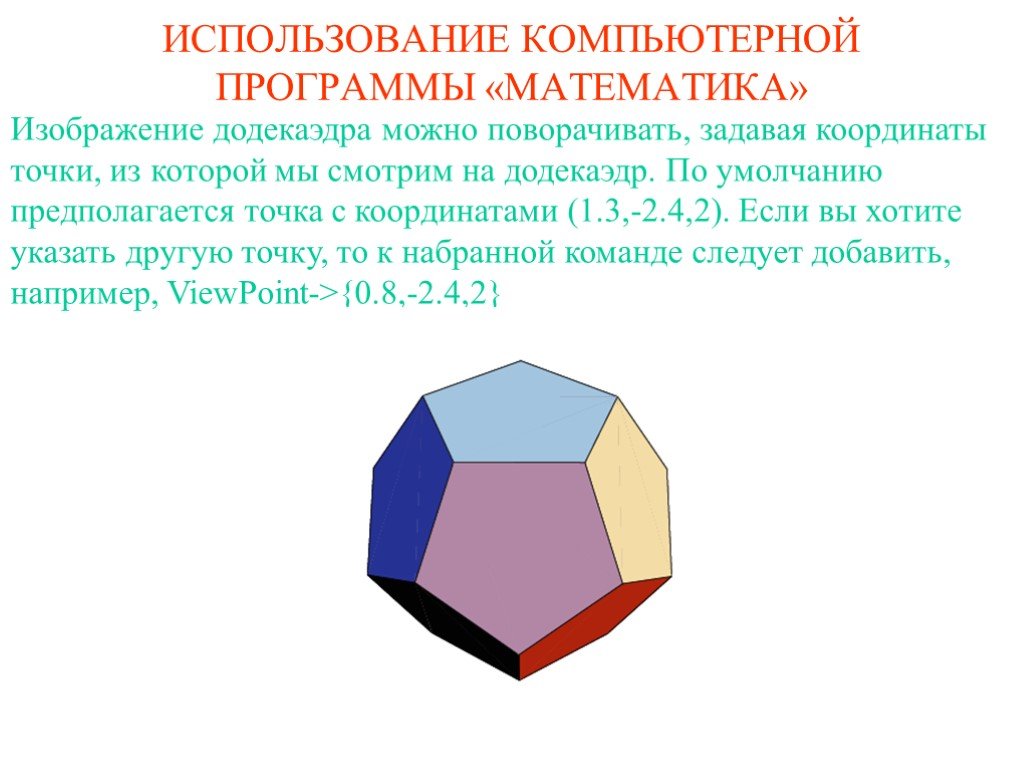
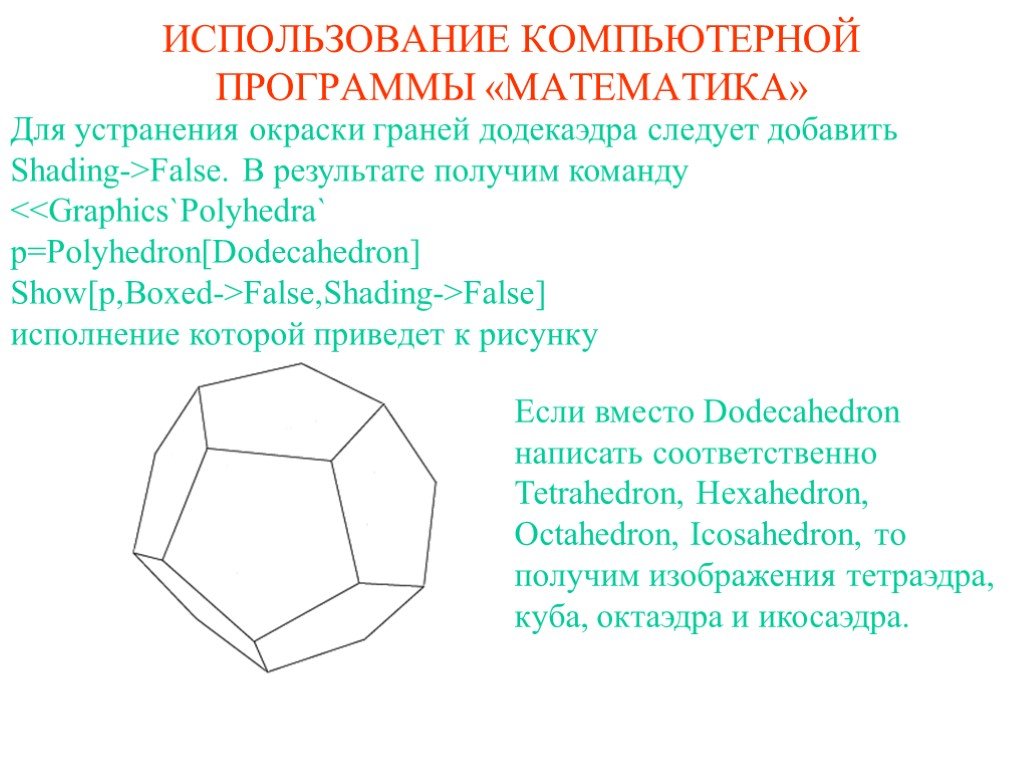
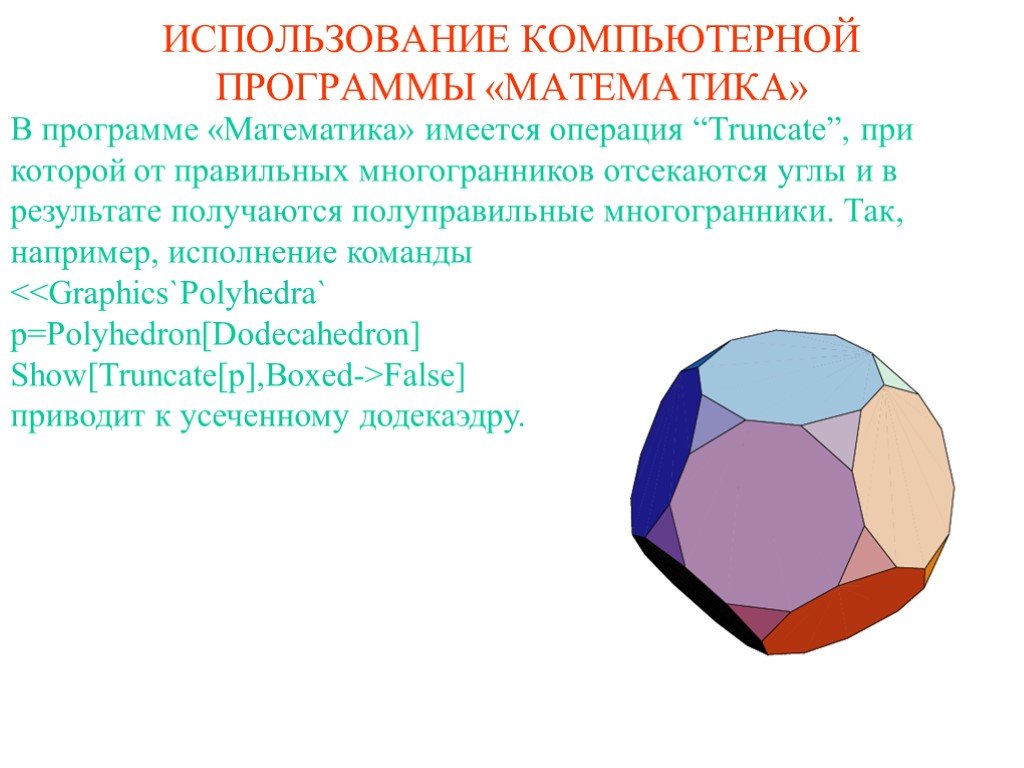















![Для устранения окраски граней додекаэдра следует добавить Shading->False. В результате получим команду False] исполнение которой приведет к рисунку. Если вместо Dodecahedron написать соответственно Tetrahedron, Hexahedron, Octahedron, Icosahedron, то получим изображения тетраэдра, куба, октаэдра Для устранения окраски граней додекаэдра следует добавить Shading->False. В результате получим команду False] исполнение которой приведет к рисунку. Если вместо Dodecahedron написать соответственно Tetrahedron, Hexahedron, Octahedron, Icosahedron, то получим изображения тетраэдра, куба, октаэдра](https://prezentacii.org/upload/cloud/19/09/164952/images/thumbs/screen4.jpg)






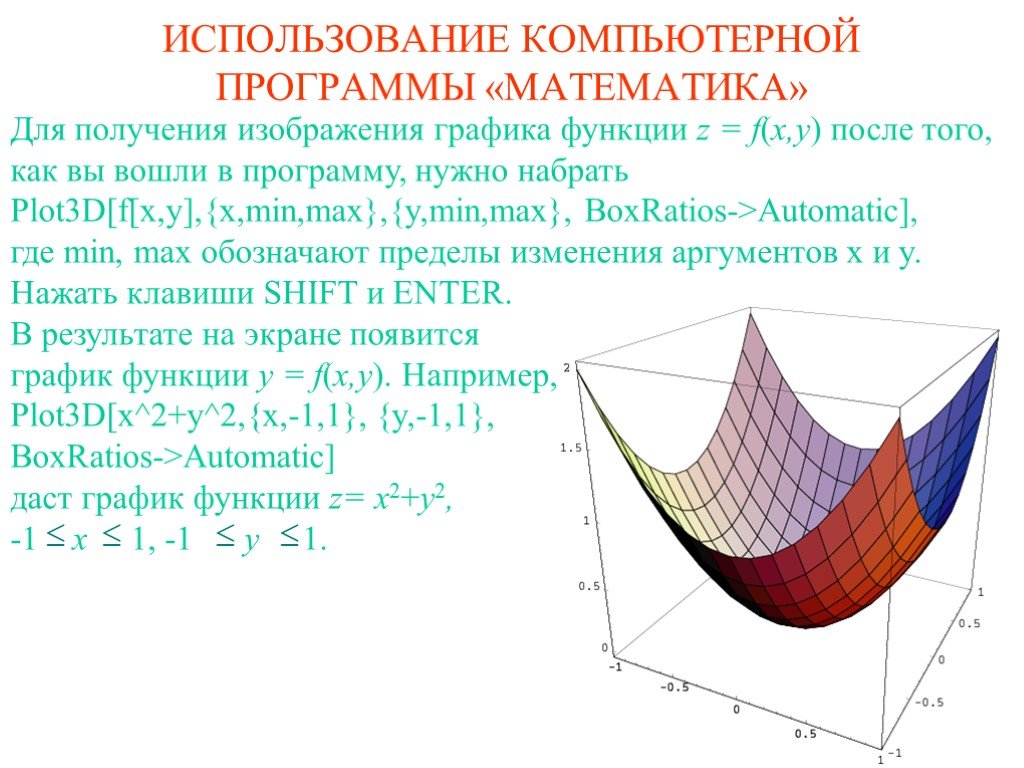
![Для получения изображения графика функции z = f(x,y) после того, как вы вошли в программу, нужно набрать Plot3D[f[x,y],{x,min,max},{y,min,max}, BoxRatios->Automatic], где min, max обозначают пределы изменения аргументов x и y. Нажать клавиши SHIFT и ENTER. В результате на экране появится график ф Для получения изображения графика функции z = f(x,y) после того, как вы вошли в программу, нужно набрать Plot3D[f[x,y],{x,min,max},{y,min,max}, BoxRatios->Automatic], где min, max обозначают пределы изменения аргументов x и y. Нажать клавиши SHIFT и ENTER. В результате на экране появится график ф](https://prezentacii.org/upload/cloud/19/09/164952/images/thumbs/screen11.jpg)

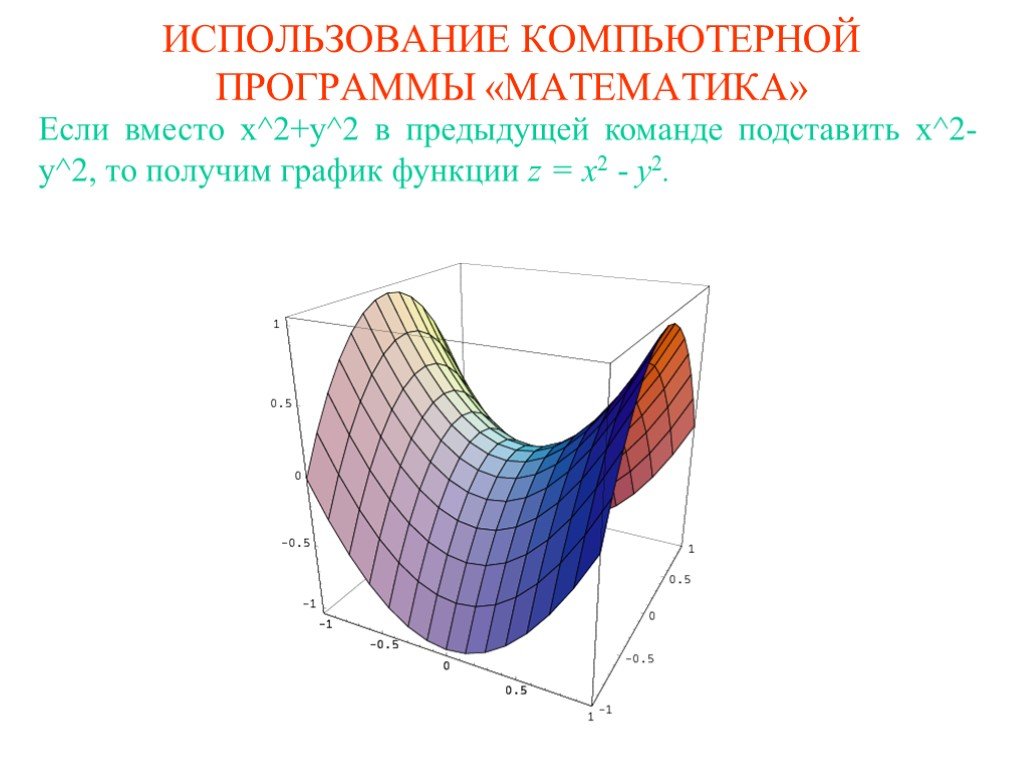
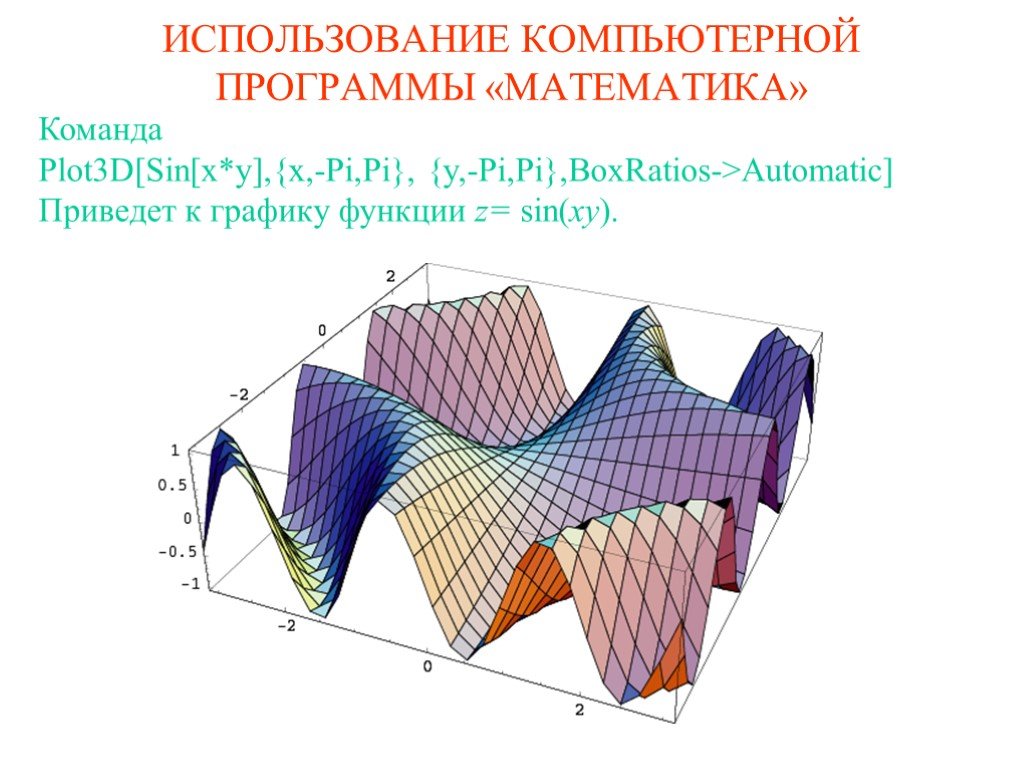
![Команда Plot3D[Sin[x*y],{x,-Pi,Pi}, {y,-Pi,Pi},BoxRatios->Automatic] Приведет к графику функции z= sin(xy). Команда Plot3D[Sin[x*y],{x,-Pi,Pi}, {y,-Pi,Pi},BoxRatios->Automatic] Приведет к графику функции z= sin(xy).](https://prezentacii.org/upload/cloud/19/09/164952/images/thumbs/screen13.jpg)
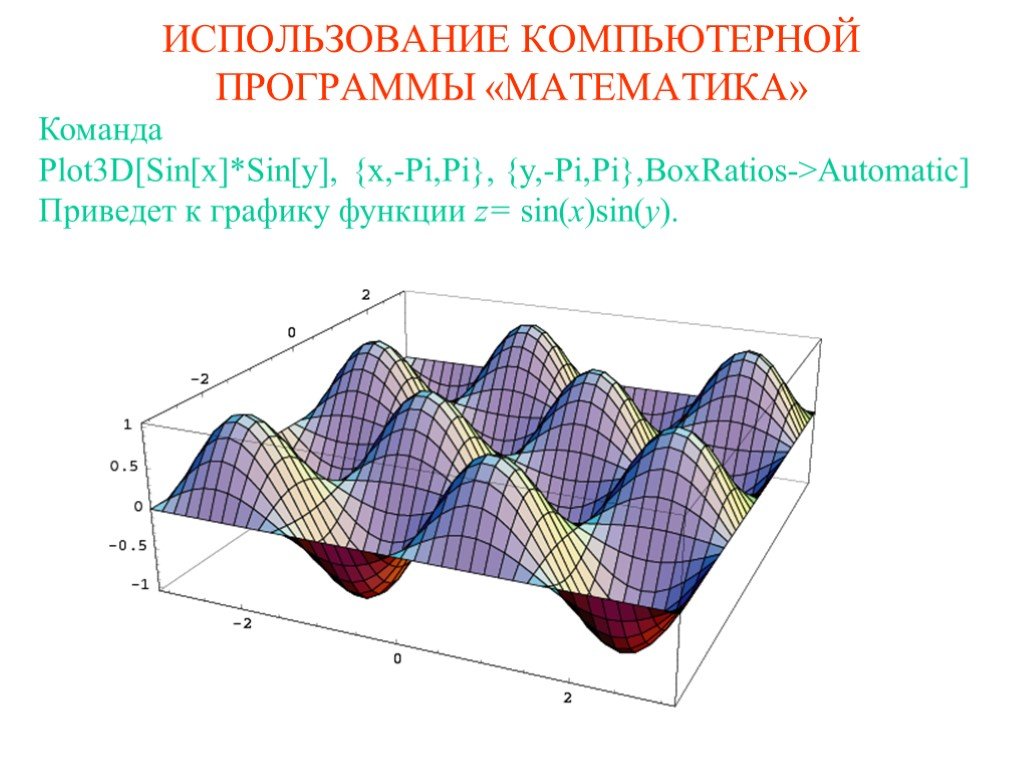
![Команда Plot3D[Sin[x]*Sin[y], {x,-Pi,Pi}, {y,-Pi,Pi},BoxRatios->Automatic] Приведет к графику функции z= sin(x)sin(y). Команда Plot3D[Sin[x]*Sin[y], {x,-Pi,Pi}, {y,-Pi,Pi},BoxRatios->Automatic] Приведет к графику функции z= sin(x)sin(y).](https://prezentacii.org/upload/cloud/19/09/164952/images/thumbs/screen14.jpg)

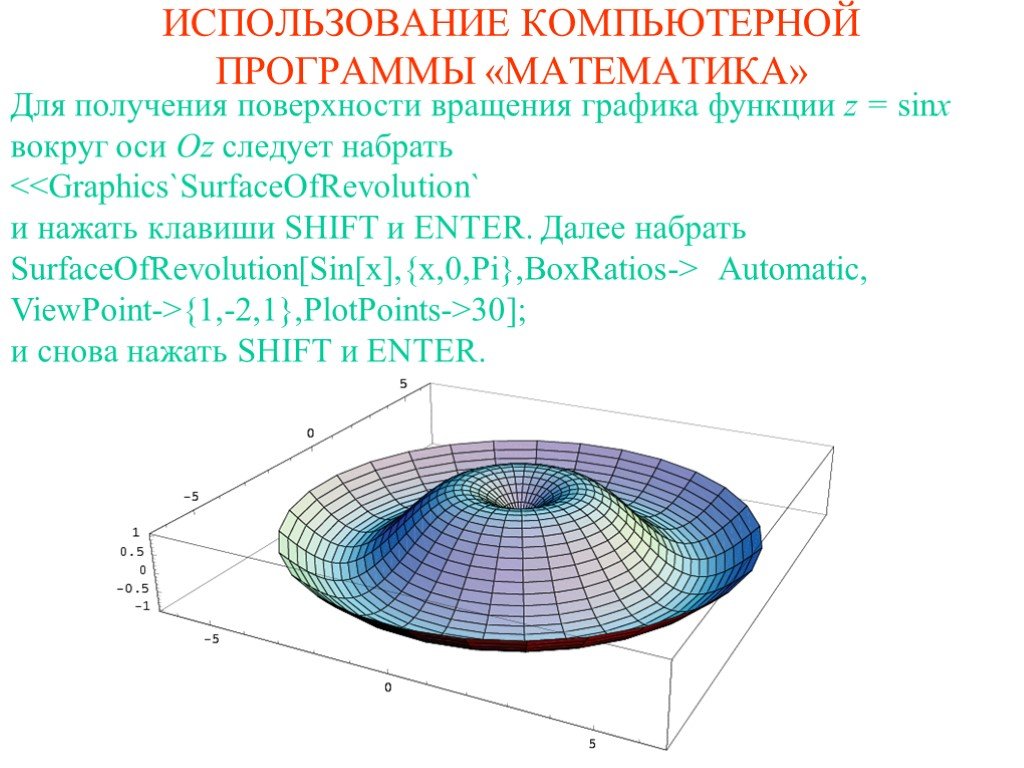
![Для получения поверхности вращения графика функции z = sinx вокруг оси Oz следует набрать {1,-2,1},PlotPoints->30]; и снова нажать SHIFT и ENTER. Для получения поверхности вращения графика функции z = sinx вокруг оси Oz следует набрать {1,-2,1},PlotPoints->30]; и снова нажать SHIFT и ENTER.](https://prezentacii.org/upload/cloud/19/09/164952/images/thumbs/screen16.jpg)
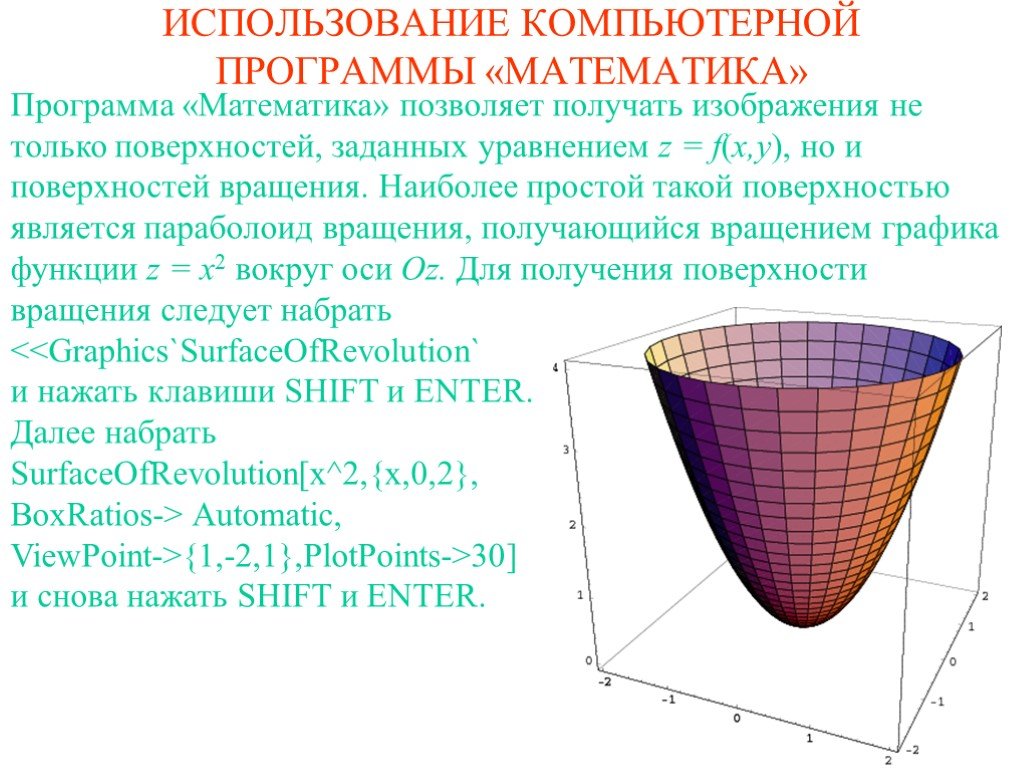
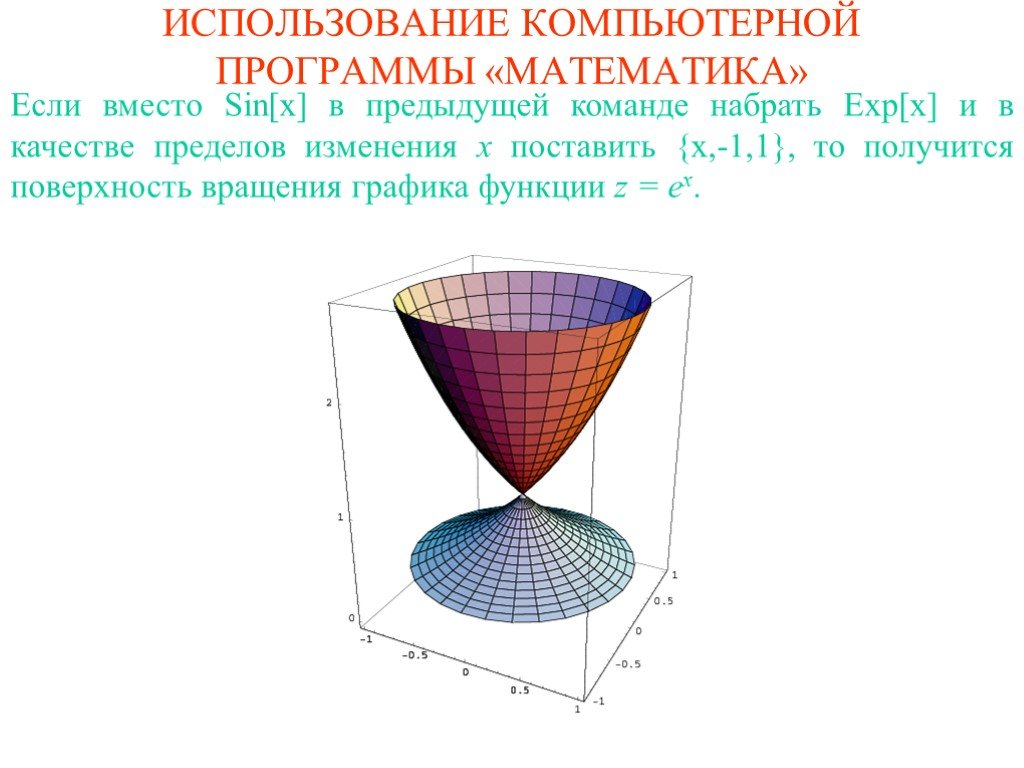
![Если вместо Sin[x] в предыдущей команде набрать Exp[x] и в качестве пределов изменения x поставить {x,-1,1}, то получится поверхность вращения графика функции z = ex. Если вместо Sin[x] в предыдущей команде набрать Exp[x] и в качестве пределов изменения x поставить {x,-1,1}, то получится поверхность вращения графика функции z = ex.](https://prezentacii.org/upload/cloud/19/09/164952/images/thumbs/screen17.jpg)
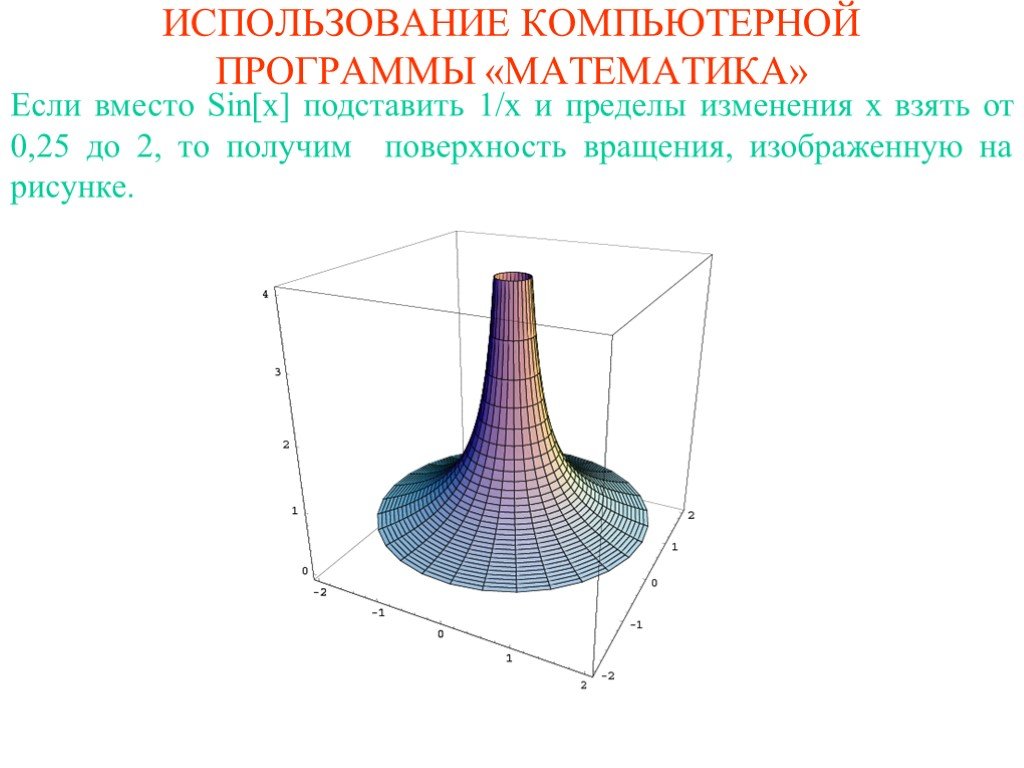
![Если вместо Sin[x] подставить 1/x и пределы изменения x взять от 0,25 до 2, то получим поверхность вращения, изображенную на рисунке. Если вместо Sin[x] подставить 1/x и пределы изменения x взять от 0,25 до 2, то получим поверхность вращения, изображенную на рисунке.](https://prezentacii.org/upload/cloud/19/09/164952/images/thumbs/screen18.jpg)
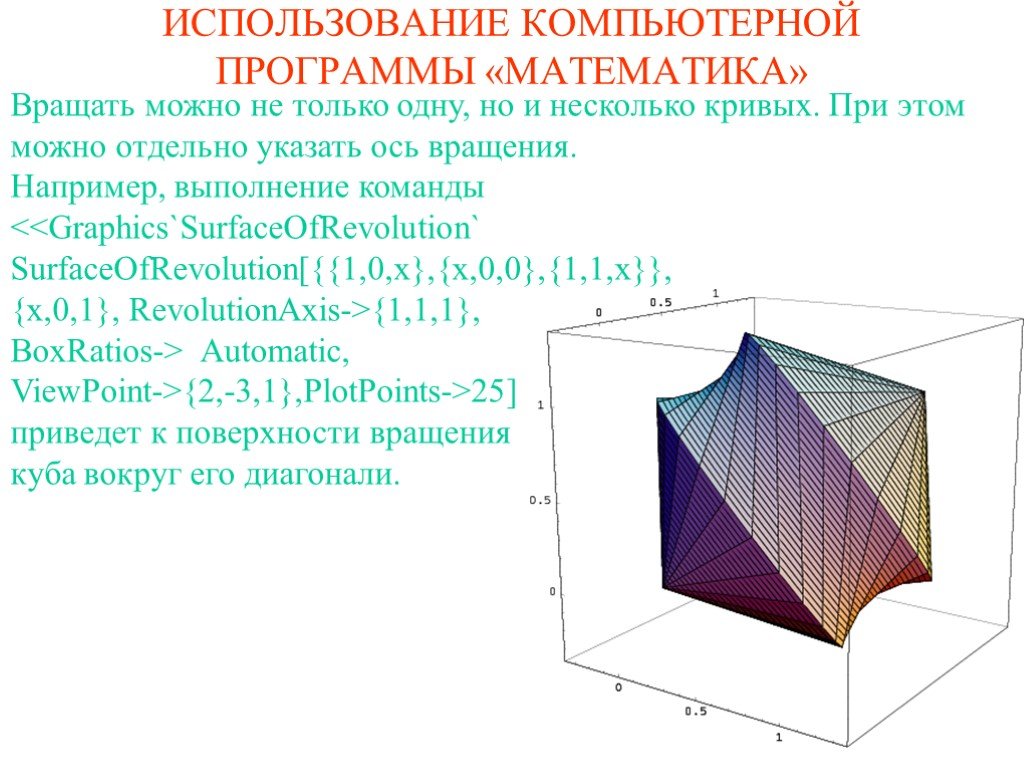
![Вращать можно не только одну, но и несколько кривых. При этом можно отдельно указать ось вращения. Например, выполнение команды Automatic, ViewPoint->{2,-3,1},PlotPoints->25] приведет к поверхности вращения куба вокруг его диагонали. Вращать можно не только одну, но и несколько кривых. При этом можно отдельно указать ось вращения. Например, выполнение команды Automatic, ViewPoint->{2,-3,1},PlotPoints->25] приведет к поверхности вращения куба вокруг его диагонали.](https://prezentacii.org/upload/cloud/19/09/164952/images/thumbs/screen19.jpg)

![В квадратных скобках можно указать величину радиуса основания, высоты и числа вершин многоугольника в основании цилиндра. Например, исполнение команды Show[Graphics3D[Cylinder[2,1,6]],Boxed->False] приводит к боковой поверхности прямой шестиугольной призмы. В квадратных скобках можно указать величину радиуса основания, высоты и числа вершин многоугольника в основании цилиндра. Например, исполнение команды Show[Graphics3D[Cylinder[2,1,6]],Boxed->False] приводит к боковой поверхности прямой шестиугольной призмы.](https://prezentacii.org/upload/cloud/19/09/164952/images/thumbs/screen21.jpg)
![Если вместо слова Cylinder, написать слово Cone, т.е. набрать Show[Graphics3D[Cone[]],Boxed->False] и снова нажать SHIFT и ENTER, то в результате получим изображение поверхности конуса. Если вместо слова Cylinder, написать слово Cone, т.е. набрать Show[Graphics3D[Cone[]],Boxed->False] и снова нажать SHIFT и ENTER, то в результате получим изображение поверхности конуса.](https://prezentacii.org/upload/cloud/19/09/164952/images/thumbs/screen22.jpg)
![В квадратных скобках можно указать величину радиуса основания, высоты и числа вершин многоугольника в основании конуса. Например, исполнение команды Show[Graphics3D[Cone[2,1,6]],Boxed->False] приводит к поверхности прямой шестиугольной пирамиды. В квадратных скобках можно указать величину радиуса основания, высоты и числа вершин многоугольника в основании конуса. Например, исполнение команды Show[Graphics3D[Cone[2,1,6]],Boxed->False] приводит к поверхности прямой шестиугольной пирамиды.](https://prezentacii.org/upload/cloud/19/09/164952/images/thumbs/screen23.jpg)
![Если вместо слова Cone, написать слово Torus, т.е. набрать Show[Graphics3D[Torus[]],Boxed->False] и снова нажать SHIFT и ENTER, то в результате получим изображение поверхности тора, поверхности, напоминающей баранку или бублик. Если вместо слова Cone, написать слово Torus, т.е. набрать Show[Graphics3D[Torus[]],Boxed->False] и снова нажать SHIFT и ENTER, то в результате получим изображение поверхности тора, поверхности, напоминающей баранку или бублик.](https://prezentacii.org/upload/cloud/19/09/164952/images/thumbs/screen24.jpg)
![Если вместо слова Torus, написать слово Helix, т.е. набрать Show[Graphics3D[Helix[]],Boxed->False] и снова нажать SHIFT и ENTER, то в результате получим изображение поверхности, которая называется геликоидом, и напоминает винтовую лестницу. Если вместо слова Torus, написать слово Helix, т.е. набрать Show[Graphics3D[Helix[]],Boxed->False] и снова нажать SHIFT и ENTER, то в результате получим изображение поверхности, которая называется геликоидом, и напоминает винтовую лестницу.](https://prezentacii.org/upload/cloud/19/09/164952/images/thumbs/screen25.jpg)