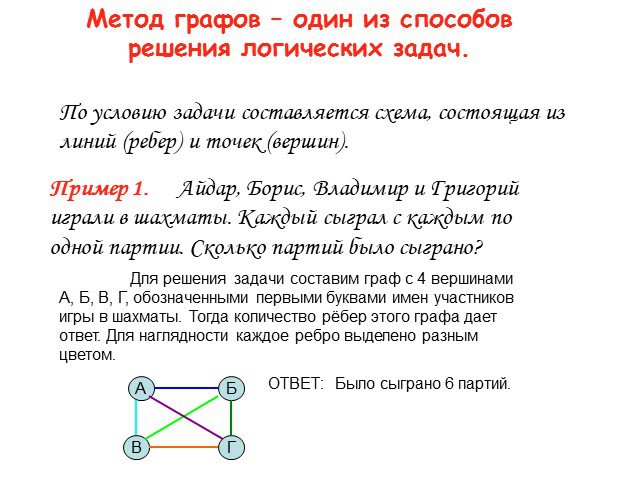
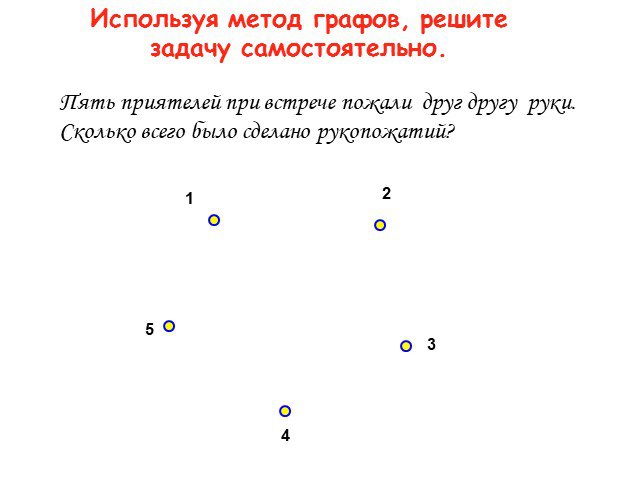
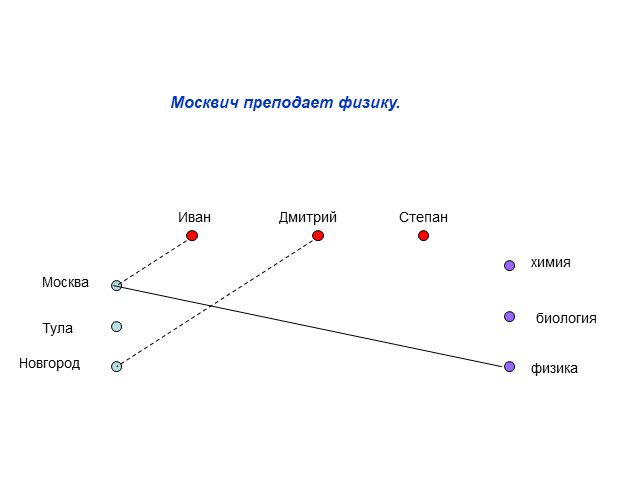
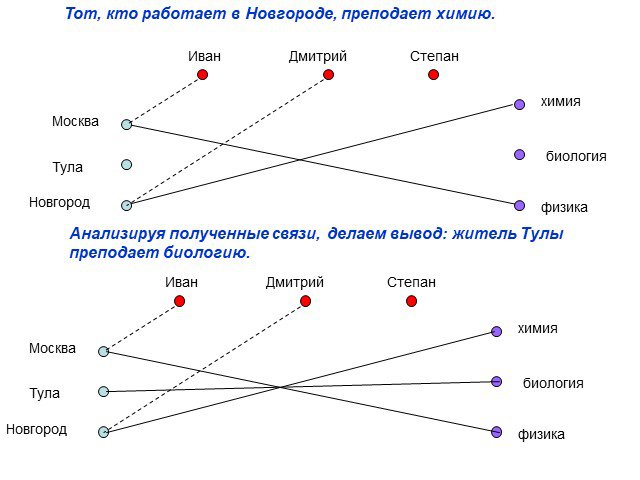
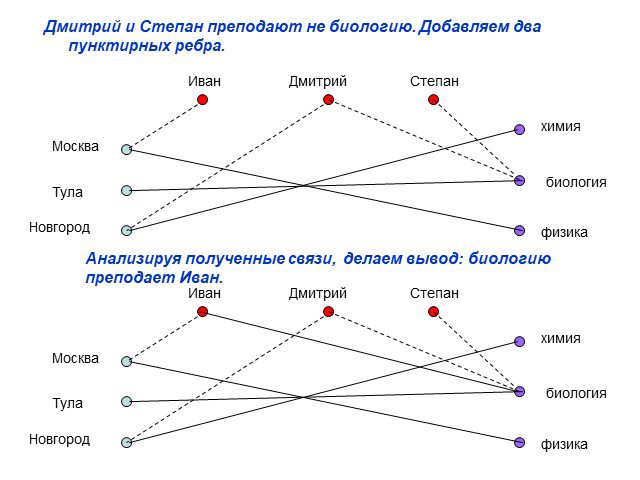
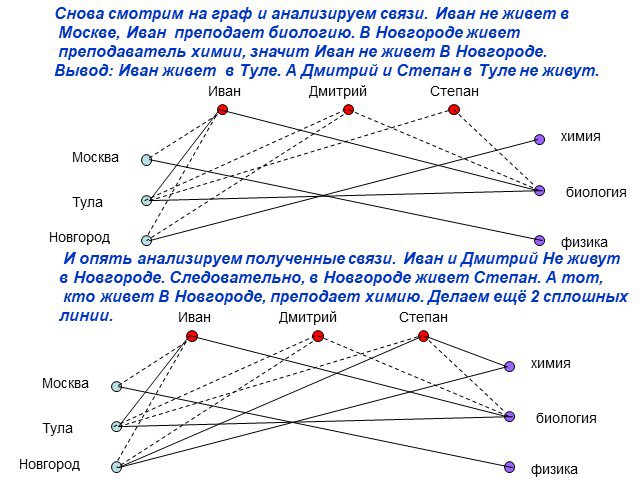
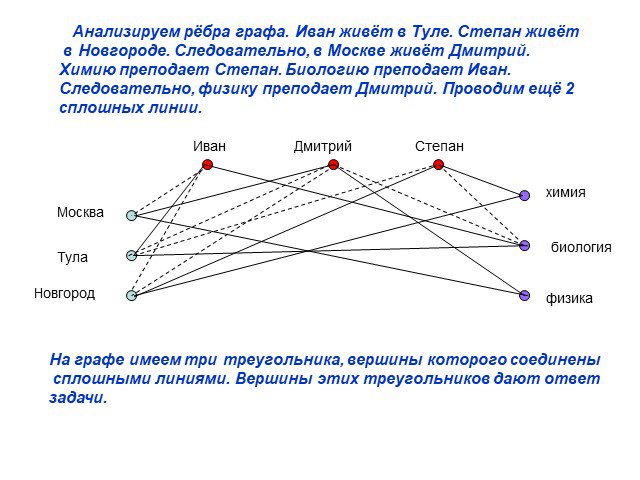
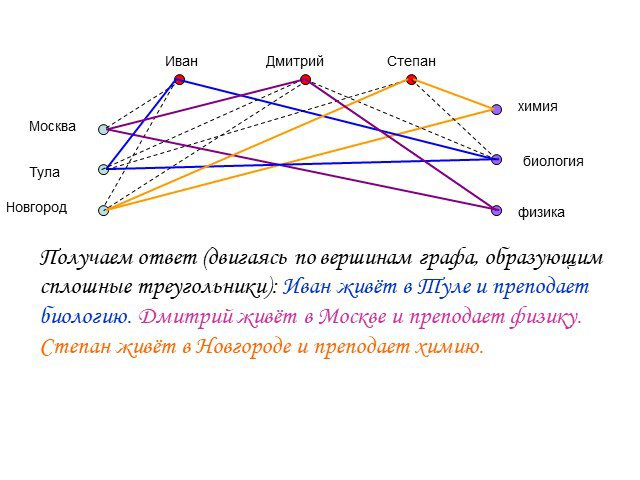
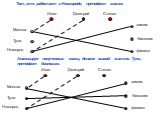
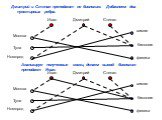
Презентация "Использование графов в решении логических задач" по математике – проект, доклад

27.12.2017

Шабанова Е.С., гимназия №39 Меркенского района

Использование графов в решении логических задач

ГРАФЫ

Графами называются геометрические фигуры, состоящие из точек (вершин графа) и линий (ребер графа), соединяющих эти точки. При этом с помощью вершин изображаются элементы некоторого множества, а с помощью рёбер –определенные связи между этими элементами.

Метод графов – один из способов решения логических задач.

По условию задачи составляется схема, состоящая из линий (ребер) и точек (вершин).

Пример 1. Айдар, Борис, Владимир и Григорий играли в шахматы. Каждый сыграл с каждым по одной партии. Сколько партий было сыграно?

Для решения задачи составим граф с 4 вершинами А, Б, В, Г, обозначенными первыми буквами имен участников игры в шахматы. Тогда количество рёбер этого графа дает ответ. Для наглядности каждое ребро выделено разным цветом. ОТВЕТ: Было сыграно 6 партий.

Используя метод графов, решите задачу самостоятельно.

Пять приятелей при встрече пожали друг другу руки. Сколько всего было сделано рукопожатий?

Прием моделирования с помощью графов.

Ситуации, в которых требуется найти соответствие между элементами различных множеств, можно моделировать с помощью графов. В этом случае элементы различных множеств будем обозначать точками, а соответствия между ними –отрезками. Пунктирные линии будут обозначать отсутствие соотношений, указанных в задаче.

Три товарища –Иван, Дмитрий и Степан преподают различные предметы (химию, биологию и физику) в школах Москвы Тулы и Новгорода. О них известно следующее : Иван работает не в Москве, а Дмитрий не в Новгороде. Москвич преподает физику. Тот, кто работает в Новгороде, преподает химию. Дмитрий и Степан преподают не биологию. Какой предмет и в каком городе преподает каждый?

Пример 2.

В задаче можно выделить три множества: учебных предметов, городов, учителей. Каждое множество содержит по три элемента. Обозначим их вершинами графа (точками).

По условию задачи будем соединять точки отрезками (сплошными линиями), если имеет место соответствие между данными элементами, или пунктирными линиями, если соответствия нет. Таким образом, рёбра нашего графа будут либо сплошные, либо пунктирные.

Построим рёбра, используя условие: Иван работает не в Москве, а Дмитрий не в Новгороде.

Москвич преподает физику.

Анализируя полученные связи, делаем вывод: житель Тулы преподает биологию.

Тот, кто работает в Новгороде, преподает химию.

Дмитрий и Степан преподают не биологию. Добавляем два пунктирных ребра.

Анализируя полученные связи, делаем вывод: биологию преподает Иван.

Снова смотрим на граф и анализируем связи. Иван не живет в Москве, Иван преподает биологию. В Новгороде живет преподаватель химии, значит Иван не живет В Новгороде. Вывод: Иван живет в Туле. А Дмитрий и Степан в Туле не живут.

И опять анализируем полученные связи. Иван и Дмитрий Не живут в Новгороде. Следовательно, в Новгороде живет Степан. А тот, кто живет В Новгороде, преподает химию. Делаем ещё 2 сплошных линии.

Анализируем рёбра графа. Иван живёт в Туле. Степан живёт в Новгороде. Следовательно, в Москве живёт Дмитрий. Химию преподает Степан. Биологию преподает Иван. Следовательно, физику преподает Дмитрий. Проводим ещё 2 сплошных линии.

На графе имеем три треугольника, вершины которого соединены сплошными линиями. Вершины этих треугольников дают ответ задачи.

Получаем ответ (двигаясь по вершинам графа, образующим сплошные треугольники): Иван живёт в Туле и преподает биологию. Дмитрий живёт в Москве и преподает физику. Степан живёт в Новгороде и преподает химию.

Однажды на отдыхе за круглым столом оказались пятеро ребят родом из Москвы, Санкт-Петербурга, Новгорода, Перми и Томска: Юра, Толя, Алеша, Коля и Витя. Москвич сидел между томичом и Витей, санкт-петербуржец - между Юрой и Толей, а напротив него сидели пермяки Алеша. Коля никогда не был в Санкт-Петербурге, а Юра не бывал в Москве и Томске, а томич с Толей регулярно переписываются. Определите, в каком городе живет каждый из ребят.

Ответ: Толя живет в Москве, Витя - в Санкт-Петербурге, Юра - в Новгороде, Коля - в Перми, а Алеша - в Томске.