Конспект урока «Использование монотонности при решении уравнений» по математике для 11 класса

Тема урока:

Использование монотонности при решении уравнений

Класс: 11

Время: 1 урок (45 минут)

Тип урока: урок-мастерская

Необходимое оборудование: доска, компьютер, проектор, раздаточные материалы

Цель урока:

• развитие системы знаний об уравнениях, при решении которых применяется монотонность функций, входящих в структуру уравнения;

• развитие группового метода работы как возможность самовыражения и самооценивания в микроколлективе.

Использование компьютера при подготовке учителя к уроку:

Стандартные программы операционной системы Windows позволяют создать такие материалы к уроку как:

1. Презентации.

2. Таблицы.

3. Практические задания.

4. Раздаточный материал.

План урока

1. Постановка проблемы – 3 минуты

2. Актуализация знаний – 10 минут

3. Исследование и решение проблемы – 27 минут

4. Рефлексия и постановка домашнего задания – 5 минут

План-конспект

1. На доске записаны дата, тема урока и задача на решение уравнения.

Задача: решить уравнение .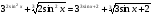

?: может ли кто-нибудь решить это уравнение? Я уверена, что к концу урока большинство из вас научится решать такие уравнения. Для этого в уравнении необходимо увидеть его структуру и использовать свойства функций, входящих в данное уравнение. Из множества свойств функций мы будем использовать сегодня монотонность. Это и является целью урока.

2. А сейчас проведем лоторею. Приглашаю любых 5 учащихся (они вытягивают номер билета и выбирают в помощники одного из учащихся). Отвечаем на вопросы билета сразу (если первый ученик не может ответить, помогает второй).

Билеты проецируются на экран.

Билет №1

1. Решить уравнение .

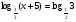2. Решить уравнение .

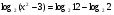Билет № 2

1. При каком условии логарифмическая функция 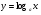возрастает?

2. Какие из перечисленных функций являются возрастающими?

; ; ; .

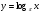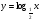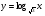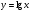Билет № 3

1. При каком условии показательная функция 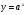убывает?

2. Какие из перечисленных функций являются убывающими?

; ; ; .

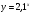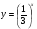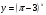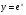Билет № 4

1. Закончите предложение: Для возрастающей функции большему аргументу соответствует … .

2. Закончите предложение: Сумма двух убывающих функций является … .

Билет № 5

1. Решите уравнение .

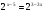2. Решите уравнение .

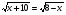3. При ответе на вопросы лотореи вы уже упоминали о возрастающих и убывающих функциях. Давайте вспомним определение монотонных функций (на экране).

Можно ли применить монотонность функций при решении уравнений? Если да, то насколько эффективно это применение? Вот основополагающие вопросы, на которые мы должны получить ответы.

Для этого мы с вами пройдем несколько этапов.

Этап 1. Как решается графически уравнение вида 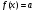, где а – некоторое число?

Ответ: строятся графики функци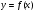й и 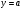, находятся абсциссы точек пересечения этих графиков.

Пусть функция 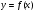- монотонная, например, строго возрастающая. Тогда прямая 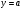может пересечь график 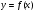не более чем в одной точке, т.е. либо вообще не пересекает, либо пересекает только в одной точке. Значит, в этом случае уравнение 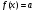или не имеет корней, или имеет единственный корень. Аналогично обстоит дело, если 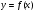- убывающая функция.

Итак, сформулируем следующее утверждение:

Если 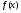- монотонная функция, то уравнение 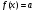имеет не более одного корня.

Пример. Слайд. Решить уравнение .

Решение. Левая часть данного уравнения – возрастающая функция (по свойству 1). Поэтому, согласно теореме, у него не более одного корня. При подстановке в уравнение 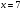получаем 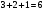, это – верное равенство. Значит, 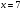- единственный корень.

Ответ: .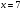

Этап 2. Пусть теперь решаем уравнение вида 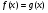, причем 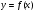- возрастающая функция, 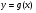- убывающая функция. Снова обратимся к графическому представлению (на доске). Получаем, что графики этих функций если пересекаются, то только в одной точке. Это представление нам поможет сформулировать так называемое утверждение о «встречной монотонности»:

Пусть функция 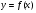возрастает на промежутке М, а функция 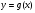убывает на этом промежутке. Тогда уравнение 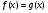имеет на промежутке М не более одного корня.

Применим эти утверждение на практике (учащиеся работают в четверках и заполняют листы)

Задания:

1. 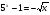; ответ: 0. Показать на доске.

2. 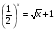; ответ: 0.

3. 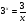; ответ: 1.

4. 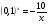; ответ: -1.

5. 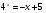; ответ: 1.

6. 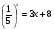; ответ: -1.

7. 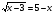; ответ: 4.

8. 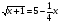; ответ: 8.

9. 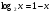; ответ: 1.

10. 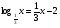; ответ: 3.

Этап 3. А теперь перейдем к более сложным уравнениям. В таких случаях лучше применять следующее утверждение:

Пусть область определения функции 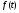есть промежуток М, и пусть эта функция непрерывна и строго монотонна (т.е. возрастает или убывает) на этом промежутке. Тогда уравнение 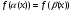равносильно системе

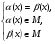
Рассмотрим пример.

Решить уравнение .

Решение: Пусть 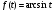. Она определена, непрерывна и возрастает на 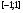(по таблице). Уравнение имеет вид 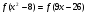. Значит, оно равносильно системе .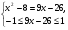

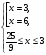
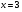Ответ: 3.

Этап 4. Работа в четверках.

Задание: Выявите функцию 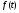, область ее определения и вид монотонности для следующих уравнений. (При этом пользуйтесь таблицей монотонности основных элементарных функций).

1. .

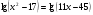2. .

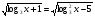3. .

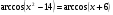4. .

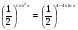Рассмотрим более сложные примеры

Пример . Решить уравнение .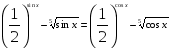

Решение. Рассмотрим функцию 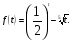Она определена, непрерывна на 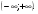Как разность убывающей функции 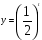и возрастающей функции 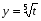функция 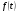убывает на 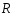. Данное уравнение имеет вид 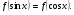Значит, по теореме 4 оно равносильно уравнению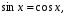

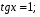
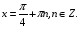
Ответ: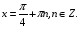

Пример. Решить уравнение .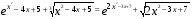

Решение. Пусть 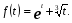Эта функция определена, непрерывна и возрастает на всей числовой прямой. Данное уравнение имеет вид:

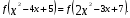Согласно теореме 4 оно равносильно уравнению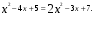

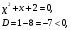
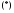значит уравнение (*), а вместе и данное уравнение корней не имеет.

Ответ: нет корней.

Решение на доске

ученик: Решить уравнение .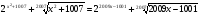

В ходе всего урока именные листы заполняются и сдаются учителю.

Ну, а теперь повторим вопрос: сможете ли решить записанное на доске уравнение?

Ответ: да!

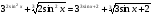провести решение этого уравнения

4. Рефлексия.

Вот теперь можно расслабиться, окинуть мысленно всю свою работу на уроке.

Итак,

- можно ли применять монотонность при решении уравнений?

- эффективно ли применение монотонности при решении уравнений? (да, некоторые уравнения просто не смогли бы решить другими методами)

- Что нового вы узнали на этом уроке?

- Какие задачи из предложенных вам понравилось решать?

- Чувствуете ли вы уверенность в данный момент перед нестандартными уравнениями?

Чтобы вы сохранили сегодняшний настрой на положительный успех, я вам предлагаю выполнить домашнюю работу: решить уравнение .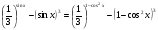

А в конце я вам предлагаю послушать научно-философскую сказку «Величественная дробь».

В математическом царстве, арифметическом государстве жила-была гордая дробь. В царстве этом властвовали строгие математические законы. Все жители – числа, цифры, переменные, знаки общались друг с другом, взаимодействовали. У них были свои компании – уравнения, неравенства и много других коллективов. Но за ними всегда следили представители закона: аксиомы, теоремы, ограничения, условия. Наш главный герой – дробь – всегда любила похвастаться перед другими. У хвастунишки были две слуги : Числитель и Знаменатель. И она все время помыкала ими. Считала себя самой главной и всегда упрекала их: «Что бы вы без меня делали?» Она очень любила унижать знаменатель, оскорбляла его, как могла. От этого Знаменатель падал духом, уменьшался, старался быть незаметным, не бросаться в глаза своей эгоистичной, гордой хозяйке. Так дробь становилась больше, ей казалось, что ее величие не знает границ.

К сожалению, дробь не одна такая. Многие люди тоже думают, что чем больше они унижают других, тем величественнее становятся. Такие люди быстро теряют друзей, и общество отворачивается от них, потому что такие люди – злостные нарушители законов морали и психологии человека.

И что же произошло с дробью? Она так много унижала Знаменатель, что тот совсем превратился в ноль. Такие обстоятельства не соответствовали требованиям математического государства, и бедная, но гордая дробь была изгнана, и все ее дальнейшее существование не имело никакого значения для великой страны бесконечных превращений и законов, которую мы, ЛЮДИ, называем МАТЕМАТИКОЙ.