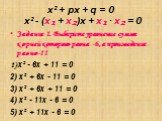Презентация "Теорема Виета" по математике – проект, доклад
Презентацию на тему "Теорема Виета" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 21 слайд(ов).
Слайды презентации
Список похожих презентаций
Теорема Виета
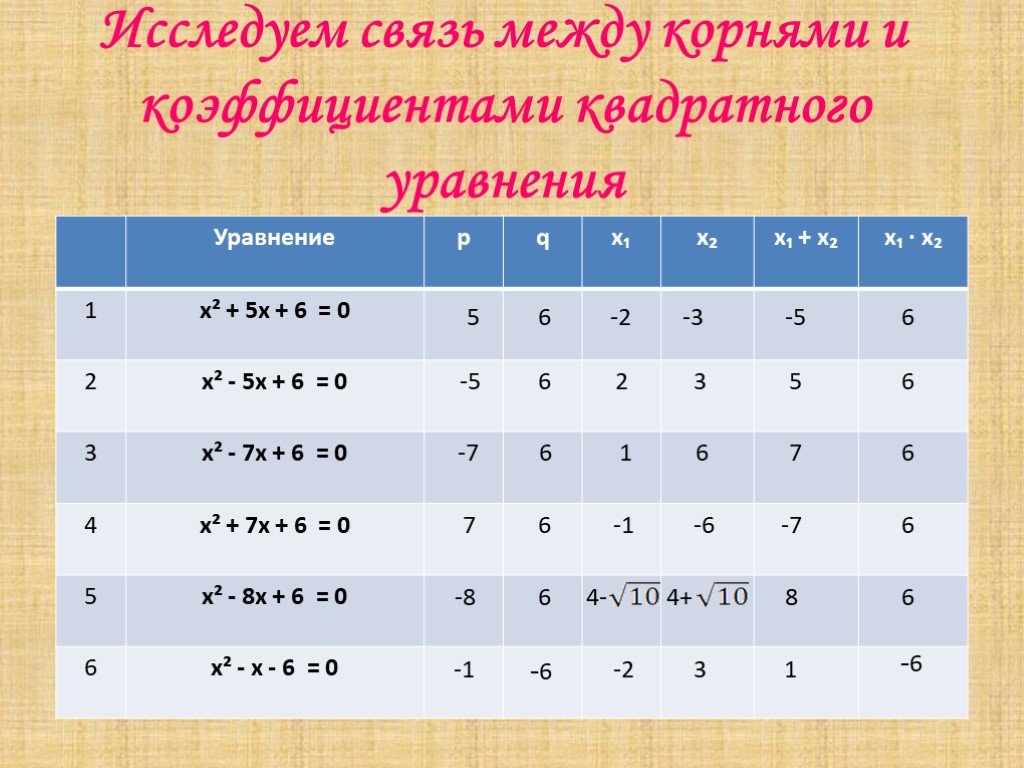
Формулировка. Если x1 и x2 – корни квадратного уравнения x2+px+q=0, то x1+x2=-p, а x1∙x2=q. С помощью теоремы Виета можно выразить коэффициенты квадратного ...Теорема Виета
Квадратное уравнение. Квадратным уравнением называется уравнение вида ax2+bx+c=0, где a, b, с R (a 0). Числа a, b, с носят следующие названия: ...Теорема Виета
Решим уравнение:. Как называется квадратное уравнение такого вида? Приведенное Чему равна сумма и произведение корней данного уравнения? 5+2=7 и 5*2=10 ...Теорема Виета
Заполнить таблицу. 3 5 6 -3 -4 -7 -1 4 -5 1 -6. Теорема Виета. Сумма корней приведённого квадратного уравнения равна второму коэффициенту, взятому ...Теорема Виета
Теорема Виета Цели урока:. Доказать теорему Виета. Научится решать квадратные уравнения применяя теорему Виета. Рассмотреть свойства коэффициентов ...Теорема Виета
Цели урока:. - повторить виды квадратных уравнений и формулы корней квадратного уравнения; - «открыть» зависимость между корнями и коэффициентами ...Квадратное уравнение и теорема Виета
Цель урока:. Повторить решение квадратных уравнений общего вида, неполных квадратных уравнений. Рассмотреть и доказать теорему Виета и сформулировать ...Теорема Пифагора. Обратная теорема. Решение задач
Цель урока:. 1. Закрепить умение применять теорему Пифагора и теорему, обратную теореме Пифагора, при решении задач, решение индийских задач. 2. Развитие ...Теорема Пифагора: доказательства
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. Формулировка теоремы. a b c. Доказательство. Различные виды доказательства ...Теорема Пифагора доказательство
Квадрат гипотенузы прямоугольного треугольника равен сумме квадратов его катетов. Елекова Э.М. Республика Алтай. Смотри и докажи! (∆ АВС- прямоугольный ...Теорема Пифагора в картинках
Мальчик прошел от дома по направлению на восток 800 м. Затем повернул на север и прошел 600 м. На каком расстоянии от дома оказался мальчик? 800 600 ...Знакомство с теоремой Виета
Виет(Вьет) Франсуа (1540-1603)-выдающийся французский математик. Его называют «отцом алгебры». КВАДРАТНЫЕ УРАВНЕНИЯ И ИХ КОРНИ:. Сумма корней приведенного ...Теорема Пифагора
Содержание. Формулировка теоремы Доказательства теоремы Значение теоремы Пифагора. Формулировка теоремы. « Доказать, что квадрат, построенный на гипотенузе ...Теорема, обратная теореме Пифагора
Теорема: Если квадрат одной стороны треугольника равен сумме квадратов двух других сторон, то треугольник прямоугольный. Дано: АВС, АВ2 = АС2 + ВС2 ...Роль Франсуа Виета в математике
Содержание. Биография Заслуги Виета Открытия Виета Теорема Виета Применение теоремы. Франсуа Виет родился в 1540 году в французской провинции. Адвокат ...Площади фигур. Теорема Пифагора
Установите соответствие между фигурой и формулой площади. . Задача № 1. В треугольнике два угла равны 45 и 90 , а большая сторона 12 см. Найдите 2 ...Теорема синусов
Вычислить площадь фигуры. Найти. высоты параллелограмма. высоту АН треугольника. Формулировка. Стороны треугольника пропорциональны синусам противолежащих ...Теорема Фалеса
Цель и задача урока. Цель данного урока знакомство с жизнедеятельностью философа и мыслителя Фалеса и его теоремой; развитие «геометрического зрения», ...Теорема Пифагора
Древний Китай Египет Карикатуры. Из книги Чу-пей. В этом сочинении говорится о пифагоровом треугольнике со сторонами 3, 4 и 5: "Если прямой угол разложить ...Теорема Пифагора
Домашняя работа. № 483(б) c² = a² + b²; c² = 5² + 6²= 61; с = . № 484 (б) b² = c² - a²; b² = 9² - 7² =32; b =. №486 (а) Решение: ∆АВС прямоугольный ...Конспекты
Теорема Виета
Открытый урок составила: Учитель математики МБОУ «Знаменской СОШ» Боградского района, Хакасия, Бондарь Нина Александровна. Тема урока: Теорема Виета ...Теорема Виета
Балабанова Лариса Юрьевна,. учитель математики. Куединского района Пермского края. МБОУ «Большеусинская СОШ». Конспект урока алгебры в ...Решение квадратных уравнений. Теорема Виета. Разложение квадратного трёхчлена на множители
Для учителя. Урок алгебры в 8 классе. . Тема:. «Решение квадратных уравнений. Теорема Виета. Разложение квадратного трёхчлена на множители». ...Теорема Виета
МОУ Новлянская средняя общеобразовательная школа. Разработка урока алгебры (сценарий) в 8 классе на тему. «Теорема Виета». . . ...Теорема Виета
Урок алгебры в 8 классе Учитель: Барсукова Н.А. Тема урока:. Теорема Виета. Тип урока:. открытие новых знаний. Технология:. проблемно – ...Теорема Виета
Урок алгебры в 8 классе. Учитель:. . Соломонова Евгения Николаевна,. МБОУ «Старицкая СОШ». Тема урока:. Теорема Виета. Тип урока:. открытие ...Теорема Виета
Урок по алгебре в 8 классе по теме «Теорема Виета». Конева Надежда Александровна, учитель математики ВКК. . МБОУ Борисоглебского городского округа. ...Теорема Виета
Астахова И.А. , учитель математики ТОГБОУ кадетская школа-интернат «Многопрофильный кадетский корпус», Г.Тамбов. Тема урока: «Теорема Виета». ...Теорема Фалеса
Конспект урока. Математика, 8 класс, учитель Селюнина Зинаида Михайловна. Тема:. Теорема Фалеса. Часов на изучение темы:. 1. . Тип урока:. ...Теорема Пифагора. Различные способы доказательства
ПЛАН-КОНСПЕКТ УРОКА. . «Теорема Пифагора. Различные способы доказательства.». . ФИО (полностью). . Поддуева Елена Вадимовна. . ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:16 августа 2019
Категория:Математика
Содержит:21 слайд(ов)
Поделись с друзьями:
Скачать презентацию