Презентация "Понятие вероятности" по математике – проект, доклад
Презентацию на тему "Понятие вероятности" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 45 слайд(ов).
Слайды презентации
Список похожих презентаций
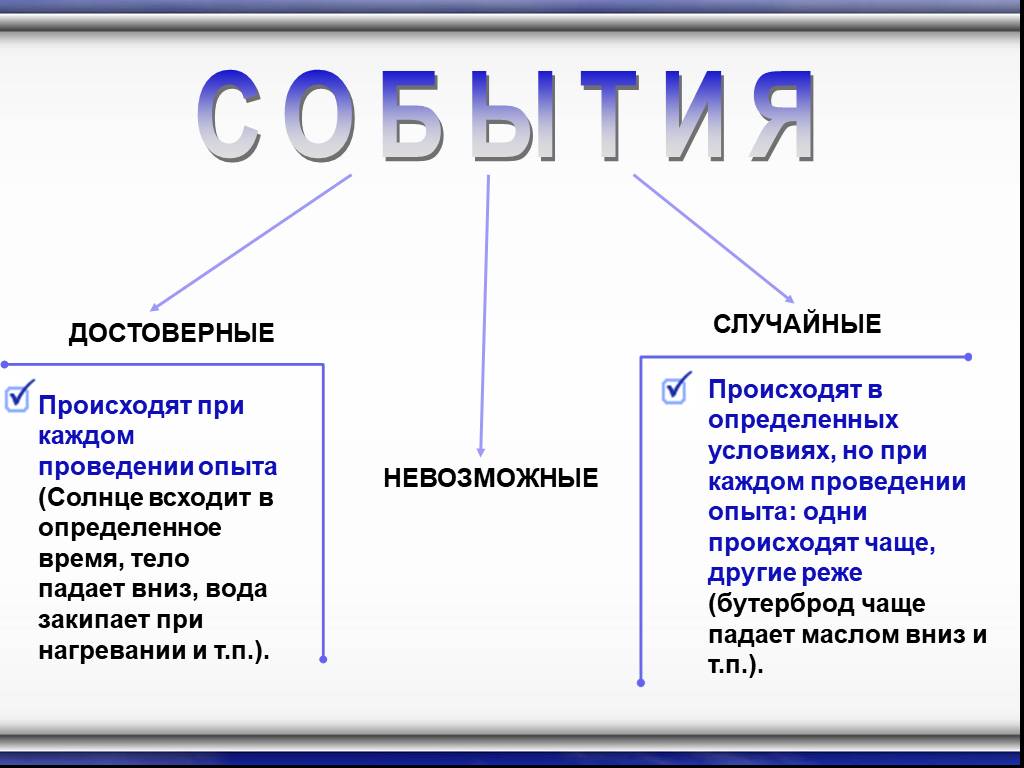
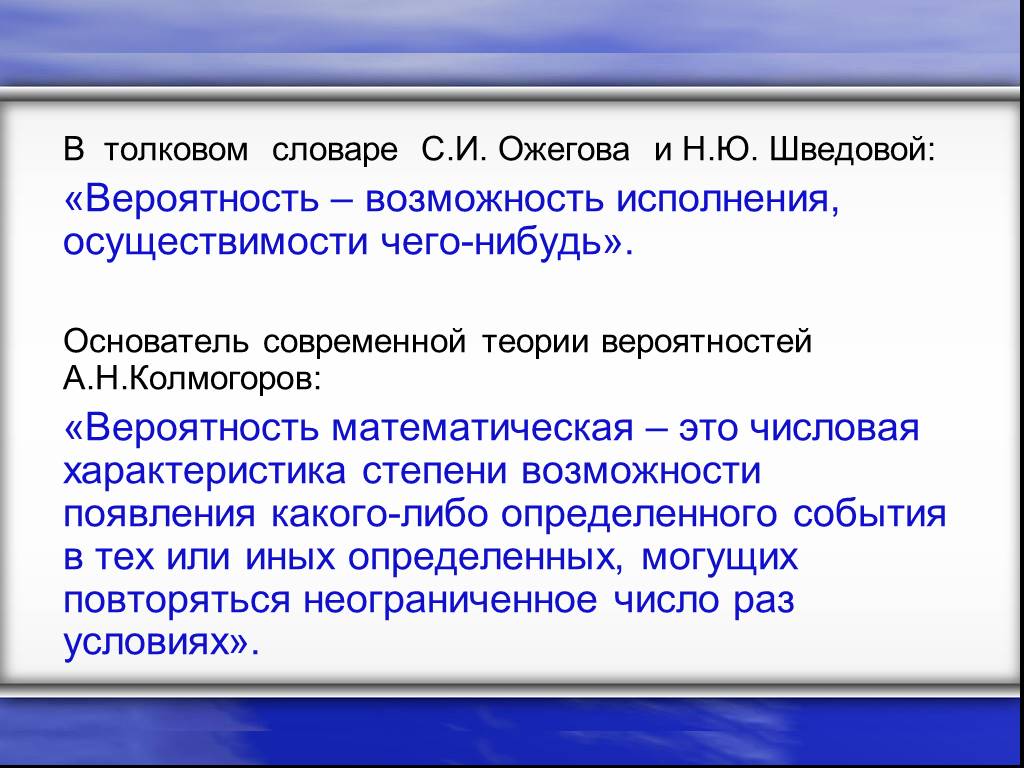
Понятие вероятности
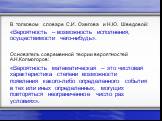
Статистическое определение вероятности. Вероятность как предельное значение частоты. Самостоятельная работа. Ошибка Даламбера. Великий французский ...Понятие центральной симметрии
Содержание:. Определение Доказательство Применение в жизни Применение в природе Решение задачи. Преобразование, переводящее каждую точку А фигуры ...Понятие угла
Готовимся к ОГЭ Вычислите:. В А. Угол поворота АОВ соответствует длине пути, пройденного точкой В от начального положения А Если подвижный вектор ...Понятие процента
ГЕНА! Я подсчитал, что старуха Шапокляк в феврале подстроила нам 19 пакостей, в марте 20, а в апреле 18. Интересно, в каком месяце она была самой ...Понятие предела функции
Определение. Пусть функция f, принимающая действительные значения, определена в некоторой окрестности точки x0, кроме, быть может, самой точки x0. ...Понятие пирамиды
Маршрут путешествия. Египет- страна Пирамид Пирамиды на Марсе Пирамиды в химии Пирамиды в экономике Пирамиды в геометрии. Путешествие вокруг света. ...Понятие объема многогранников. Объем прямоугольного параллелепипеда
1. О понятие объема тела. Аналогия с S M S(M) Равные многоугольники имеют равные площади. Площадь многоугольника равна сумме площадей составляющих ...Теория вероятности события
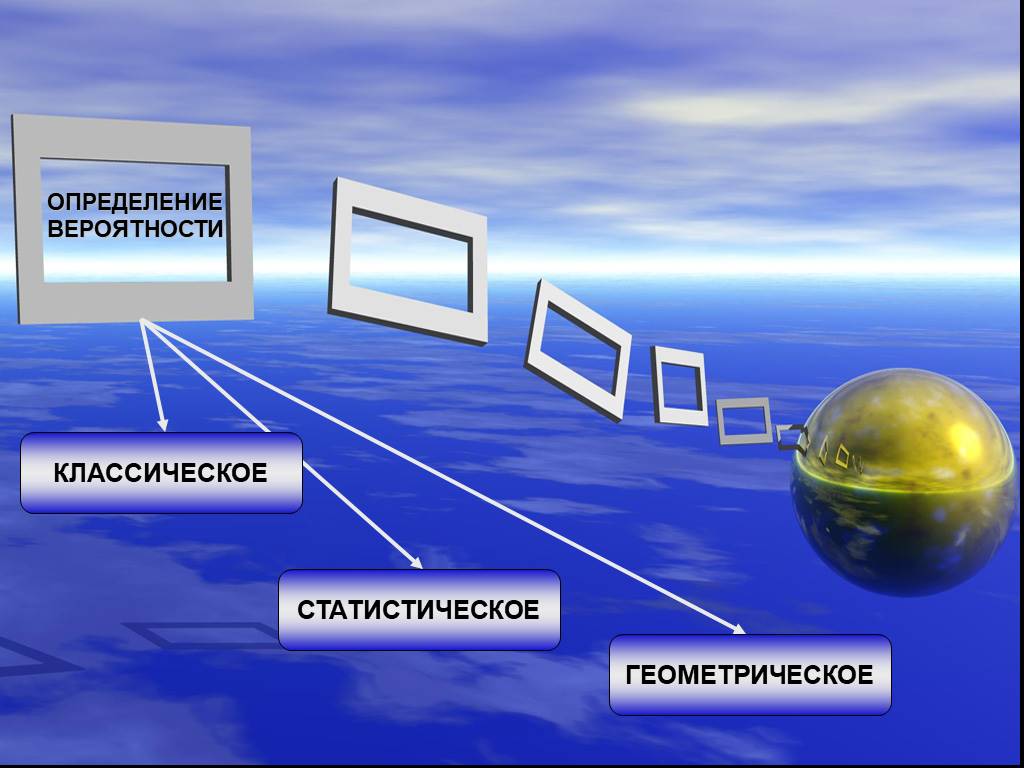
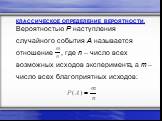
Введение в комбинаторику. В математике существует немало задач, в которых требуется из имеющихся элементов составить различные наборы, подсчитать ...Классическое определение вероятности
Тема: Классическое определение вероятности Цель: -создать условия для осознания и осмысления блока новой учебной информации. Задачи: -Способствовать ...Классическое определение вероятности
Цель урока: Выработать умение решать задачи на определение классической вероятности с использованием основных формул комбинаторики. Оборудование: ...Классическая теория вероятности
Актуальность. Актуальность изучения данной темы заключается в том, что некоторые задачи, которые ставит перед нами реальная жизнь нельзя решить без ...История теории вероятности
Человечество всегда стремилось к некоторого рода предсказаниям. Любая наука основана на этом. Однако предвидение фактов не может быть абсолютным, ...Исследование жизненных ситуаций с помощью классического определения вероятности и решение простейших задач
Цель – научить учащихся вычислять вероятности в задачах, описывающих жизненные ситуации Задачи : знакомство с языком теории вероятностей; рассмотрение ...Задачи по вероятности
Номера задач № 1104 № 1105 № 1106 № 1107 № 1108 № 1109 № 1110 № 1111 № 1112 № 1113 № 1114 выход. В колоде 36 карт, из них наугад вынимают одну карту. ...Десятичные дроби. Понятие десятичной дроби
Немного истории. Дроби, как известно, возникли в связи с делением предметов на несколько частей. При решении разных практических задач возникали дроби ...Решение задач В ЕГЭ по теории вероятности
Основные понятия теории вероятностей. Случайным называется событие, которое нельзя точно предсказать заранее. Оно может либо произойти, либо нет. ...Теория вероятности
Автор проекта ученица 10 класса «А» ГОУ СОШ № 420 г. Москвы Лавренова Юлия Руководитель проекта учитель математики ГОУ СОШ № 420 г. Москвы Афанасьева ...Комбинаторика и теория вероятности
Комбинаторика. «комбинаторика» происходит от латинского слова combinare – «соединять, сочетать». Определение. Комбинаторика – это раздел математики, ...Понятие о сложности вычислений
Под алгоритмом обычно понимают четко определенную последовательность действий, приводящую через конечное число шагов к результату — решению задачи, ...Математическая статистика и теория вероятности
Группы и специальности потоков. 92... Электроэнергетические системы и сети (100200) - 140205 93... Электроснабжение (100400) - 140211 94... Релейная ...Конспекты
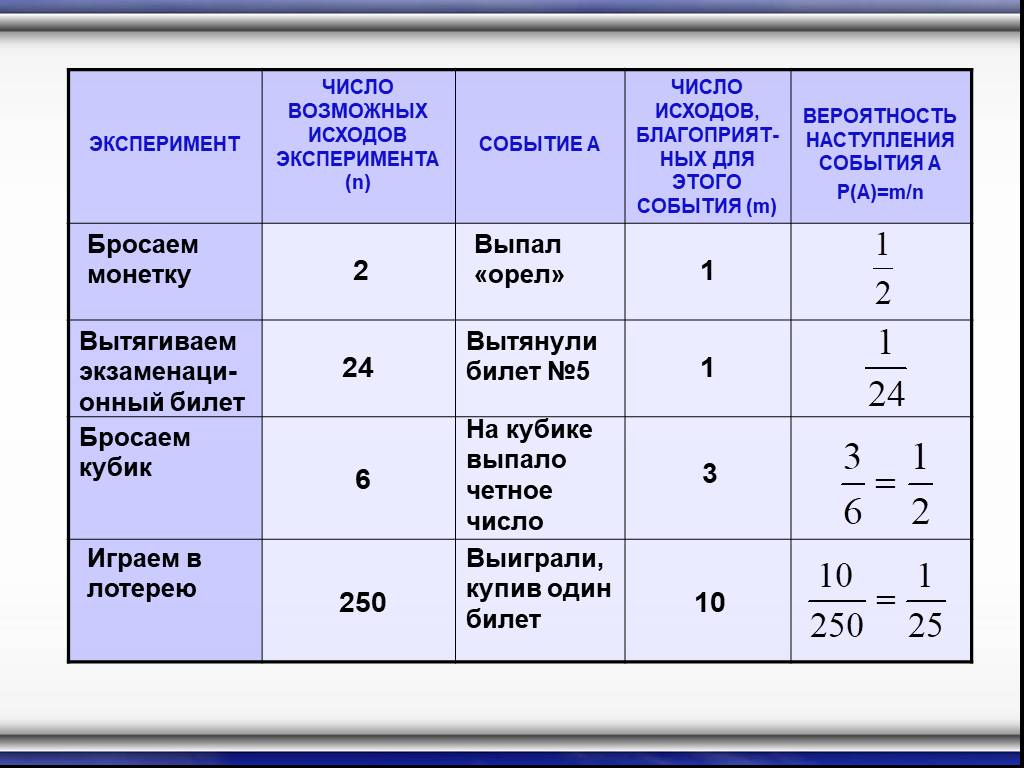
Понятие вероятности. Подсчёт вероятности
ПЛАН-КОНСПЕКТ УРОКА. . «Понятие вероятности. Подсчёт вероятности» Цель урока: Организация деятельности учащихся по формированию понятия вероятности, ...Понятие о вероятности
Конспект урока. Класс. : 5. Тема урока. : Понятие о вероятности. Цели урока. Обучающая. : познакомить учащихся с понятием вероятности, формировать ...Понятие о вероятности. Решение задач
Конспект урока. Класс. : 5. Тема урока. : Понятие о вероятности. Решение задач. Цели урока. Обучающая. : формировать умения и навыки вычисления ...Понятие о скорости. Задачи на нахождение скорости движения
План-конспект урока по математике (4класс). Учитель Ленинской Ош красногвардейского района Республики Крым. Тема. : Понятие о скорости. Задачи ...Элементы теории вероятности в ГИА
13 апреля 2011г. Урок алгебры в 9 классе по теме:. . «Элементы теории вероятности в ГИА». Цели:. - Научиться анализировать и решать задачи ...Нумерация чисел в пределах 1000. Понятие о сотне как новой счетной единице
Тема:. Нумерация чисел в пределах 1000. Понятие о сотне как новой счетной единице. 5 класс специальной (коррекционной) школы. Цели:. . . Познакомить ...Понятие вектора
Учитель математики - Юшина Раиса Алексеевна. . МБОУ СОШ № 18. . . Тема:. 9КЛ. . 2010. год. Тема:. Понятие ...Элементы комбинаторики, статистики и теории вероятности
Урок-соревнование. по разделу. «Решение задач по теме «Элементы комбинаторики, статистики и теории вероятности». г.Новороссийск, ...Понятие процента
Конспект урока по математике в 5 классе. тема урока «Понятие процента». Автор: Кирпина Татьяна Яковлевна, учитель математики МАОУСОШ № 1 г. Окуловка ...Понятие смешанной дроби
ФИО автора: Чемерова Татьяна Владимировна. Место работы:. МБОУ СОШ №3 г. Петровска Саратовской области. Должность:. учитель математики. Предмет:. ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:12 мая 2019
Категория:Математика
Содержит:45 слайд(ов)
Поделись с друзьями:
Скачать презентацию